Нақты сандар және олардың қасиеттері

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 37 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Н. Құлжанова атындағы Торғай гуманитарлық колледжі

КУРСТЫҚ ЖҰМЫС

Тақырыбы: Нақты сандар және олардың қасиеттері

Математика

Орындаған: II курс студенті Алимгереев Д.

Жетекшісі:

Арқалық - 2012ж.

МАЗМҰНЫ:

I Кіріспе

II Негізгі бөлім

2. 1 Натурал сандар және олардың қасиеттері

2. 2 Бүтін сандар және оларға амалдар қолдану

2. 3 Рационал және иррационал сандар

2. 4 Нақты сандар және олардың қасиеттері

III

2. 1 Нақты сандар және оларды салыстыру, жуықтау

2. 2 Нақты сандар қасиеттері және ережелері

2. 3 Көрсеткіштік дәреже және олардың қасиеттері

Қорытынды

Пайдаланылған әдебиеттер

КІРІСПЕ

Сан ұғымы өте ерте заманда туған. Бұл ұғым ғасырлар бойы кеңейтіліп әрі жалпылана түскен. Адамзат мәдениетінің тууы және оның дамуымен тығыз байланысты ұғым - сан ұғымы. Тарихтан бұрынғы заманда сан ұғымының тууы және дамуы тіл дамуымен байланысты болды, өйткені әр санды атау үшін тіл керек. Міне осы мәселелерді материалистік тұрғыдан талдап, танып білу жаратылыстану ғылымдар философиясындағы мақсаттардың бірі болып табылады. Буржуазиялық идеалистік «теория» сан ұғымы адамға туа біткен табиғи категория деп тұжырымдайды. Неміс математигі Кронекер « 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, . . . натурал сандарды жасаған құдай, қалғандары -адамзаттың қолындағы іс» дейді.

Математиканың алғашқы ұғымы - сан ұғымының тууына түрткі болған адамның еңбек әрекеті. Еңбектену әрекетінде оған бұйымның мөлшерін өлшеп білу керек болды. Әрине бұл ұғым бір күннің, әйтпесе бір жылдың тіпті бір ғасырдың ішінде қалыптаса қойған жоқ. Сан ұғымының қалыптасуына мыңдаған жылдар керек болды.

Адамзат мәдениет есігін аша бастаған шақта, ең алдымен натурал сандарды қолданды. Олар мыналар: 1, 2, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, . . . жеке заттарды санаудың нәтижесінен келіп шыққан бұл сандар адамзат мәдениетінің ең негізгі табыстарының бірі болып табылады. Егер сан ұғымы болмаса, рухани өміріміз бен практикалық қызметімізді өз дәрежесінде көрсете алмаған болар едік, есеп-қисап жүргізу, уақытты, қашықтықты өлшеу, еңбек нәтижелерінің қорытындыларын есептеп шығару сан ұғымынсыз мүмкін болмаған болар еді.

Теңдеулерді шешу теріс сандардың шығуына алып келді. Теріс сандар ұзақ уақыт бойы “жалған” сандар деп есептеліп, “қарыз” (“борыш”), “жеткіліксіздік” (“жетімсіздік”) ретінде түсіндіріліп келген.

Оң және теріс сандарға амалдар қолдану ережесі ұзақ уақыт бойы тек қосу және азайту жағдайлары үшін ғана ғарастырылып отырған.

XVII ғасырда ғана Декарт пен Ферма енгізген координаттар әдісі пайдаланыла бастағаннан бері теріс сандар оң сандар мен тең праволы сандар ретінде қабылданады. Бүтін және бөлшек сандар рационал жиынын құрайды. Бұл сандар есептеуге қолайлы: екі рационал санның қосындысы, айырмасы, көбейтіндісі және бөліндісі рационал сандар болып табылады.

Рационал сандардың тығыздық қасиеті бар, мұның арқасында кез келген кесіндісі бірлік өлшем ретінде қабылданған кесіндімін кез келген дәлдік дәрежесі бойынша өлшеуге және де өлшеу нәтижесін рационал санмен өрнектеуге болады. Сондықтан рационал сандар ұзақ уақыт бойы адамзаттың іс жүзінде қажеттіктерін толық қамтамасыз етіп келді (және де қазіргі кезге дейін қамтамасыз етуде) . Соған қарамастан шамаларды өлшеу мәселесі жаңа сан, иррационал санның шығуына әкеп тіреді. Ежелгі Грецияда Пифагордың (біздің заманымызға дейінгі 6 ғасырда) мектебінде, егер өлшеу бірлігі ретінде квадраттың қабырғасы алынатын болса, онда квадраттың диагоналын рационал санмен өрнектеуге болмайтыны дәлелденген болатын. Квадраттың диагоналы және оның қабырғасы секілді кесінділерді өлшенбейтін кесінділер деп атаған. Бұдан кейінгі уақытта (біздің заманымызға дейінгі 5-4 ғасырларда) ежелгі грек математиктері толық квадрат болмайтын кез келген натурал n саны үшін n санының иррационалдығын дәлелдеді.

Әрбір рационал немесе иррационал сан координаттық түзудің бойында нүктемен кескінделеді және керісінше, координаттық түзудің бойындағы әрбір нүктеге белгілі бір рационал немесе иррационал, яғни нақты сан сәйкес келеді. Иррационал сандар ендірілгеннен кейін координаттық түзудің бойындағы барлық “бос орындар” толтырылды. Осы қасиетке сүйеніп, нақты сандар жиыны үздіксіз болып табылады делінеді.

Кез келген нақты санды шектеусіз (периодты немесе периодсыз) ондық бөлшек түрінде көрсетуге болады. XVIII ғасырда Л. Эйлер (1707-1783) мен И. Ламберт (1728-1777) кез келген шектеусіз ондық бөлшек иррационал сан болатынын көрсетеді. Шектеусіз ондық бөлшектер негізінде нақты сандар құруды неміс математигі К. Вейерштрасс (1815-1897) жасады. Нақты сандар теориясын мазмұндаудың басқаша тәсілдерін неміс математиктері Р. Дедекинд (1831-1897) пен Г. Кантор (1845-1918) ұсынды.

Курстық жұмыстың мақсаты:

Нақты сандар және олардың қасиеттері туралы үйрену және олардың қасиеттерін зерттеу. Арифметикалық амалдар қолдану арқылы есептер шығару арқылы тақырыпты пысықтау. Теорияда берген материалдары тәжірибеде іске асыру.

Курстық жұмыстың міндеттері:

- санның шығу тарихы туралы түсінік беру;

- мектеп курсында оқытылатын сандар туралы түсінік қалыптастыру;

- сандардың қасиеттерін ұғындыру;

- әр түрлі қасиетке ие болатын сандарды зерттеу.

Жұмыстың зерттелу деңгейі:

Егер сандар туралы тереңірек зерттеп, оқып үйренсе, онда әрбір адам математиканың қаншалықты қажеттілігін толық түсінер еді.

Сандар мен оларға қолданылатын амалдардың қасиеттері зерттелетін математиканың бөлімі сандар теориясы деп аталады. Сандар теориясын құрудың бастамасын ежелгі грек оқымыстылары Пифагор, Евклид, Эратосфен және т. б. жасаған еді.

1. Нақты сандар жиыны

1. 1 Натурал сандар және олардың қасиеттері

Натурал сандардың жазылуы. Заттарды санау үшін немесе қандай да бір заттың біртекті заттар арасындағы реттік номерін көрсету үшін пайдаланылатын 1, 2, 3, 4, 5 . . . сандары натурал сандар деп аталады. Ондық санау системасында кез келген натурал сан 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 цифрларының көмегімен жазылады. Мысалы, 2457 жазылуы 2 - мыңдықтар цифры, 4 - жүздіктер цифры, 5 - ондықтар цифры және 7 - бірліктер цифры екенін білдіреді, яғни 2457 - 2 ∙ 1000 + 4 ∙ 100 + 5 ∙ 10 + 7. Жалпы, егер a - мыңдықтар цифры, b - жүздіктер цифры, c - ондықтар цифры және d - бірліктер цифры болса, онда a ∙ 1000 + b ∙ 100 + c ∙ 10 + d санын аламыз. Сондай-ақ, қысқаша abcd (abcd деп жазуға болмайды, өйткені бұндай жазуды математикада қабылданған келісім бойынша a, b, c, d сандарының көбейтіндісін білдіреді) жазылуы да пайдаланылады. Осы сияқты abcde жазылуы a ∙ 1 + b ∙ 1000 + c ∙ 100 + d ∙ 10 + e (a ≠ 0) санын білдіреді.

Натурал сандарға қолданылатын амалдар.

Екі натурал санды қосудың немесе көбейтудің нәтижесі әрқашан натурал сан болады: егер m, n натурал сандар болса, онда p = m +n де натурал сан, m мен n - қосылғыштар, p - қосынды; p = mn де натурал сан, m, n - көбейткіштер, p - көбейтінді. Натурал сандарды қосу мен көбейтудің келесі қасиеттері орынды:

1°. a + b = b + a (қосудың орын ауыстырымдылық қасиеті) .

2°. ( a + b) + c = a + (b + c) (қосудың терімділік қасиеті) .

3°. ab = ba (көбейтудің орын ауыстырымдылық қасиеті) .

4°. ( ab) c = a(bc) (көбейтудің терімділік қасиеті) .

5°. a (b + c) = ab + ac (көбейтудің қосуға қатысты үлестірімділік қасиеті) .

Натурал сандарды азайтудың немесе бөлудің нәтижесінде әрқашан натурал сан алына бермейді: мысалы, 7 - 4 = 3 - натурал сан, ал 4 - 7 = -3 - натурал сан емес; 21 : 7 = 3 - натурал, ал 11 : 2 = 5, 5 - натурал сан емес. Егер m, n, k - натурал сандар болса, онда m - n = k , болған жағдайда m - азайғыш, n - азайтқыш, k - айырым дейді; m : n = k болған жағдайда m - бөлінгіш, n - бөлгіш, k - бөліндінің мәні дейді, бұл жағдайда m санын n санының еселігі, ал n санын m санының бөлгіші деп те айтады. Егер m - n санының еселігі болса, онда m = kn болатындай k натурал саны табылады. Сандардан арифметикалық сандардың таңбалары (белгілері) мен жақшалардың көмегімен сандық өрнектер құрылады. Егер сандақ өрнекте, қабылданған ретті сақтай отырып, көрсетілген амалдарды орындайтын болсақ, онда өрнектің мәні деп аталатын сан алынады. Сандық өрнектерде арифметикалық амалдардың орындалу ретін еске түсірейік: алдымен жақшалардың ішіндегі амалдар орындалады; кез келген жақшалардың ішінде (жақшалар жоқ болатын өрнектерде де ауд. ) алдымен көбейту мен бөлу, ал содан кейін қосу мен азайту амалдары орындалады. Мысалы, егер

1 4 2 3 5 6

(28 ∙ 93 + (1927 - 1873) ∙ 31) : 6 - 710

өрнегінің мәнін есептеу керек болса, онда амалдардың орындалу реті мынадай болады:

1 2 3 4 5 6

(28 ∙ 93 + (1927 - 1873) ∙ 31) : 6 - 710

Қалдықпен бөлу. Егер m натурал саны n натурал санына бөлінбейтін, яғни m = nk болатындай k натурал саны жоқ болса, онда қалдықпен бөлуді қарастырады мысалы, 43 санын 18 санына бөлгенде бөліндіде 2 және қалдықпен 7 алынады, яғни 43 = 18 ∙ 2 + 7. Жалпы жағдайда, егер m - бөлінгіш, n - бөлгіш ( m > n), p - бөлінді және r - қалдық болса, онда

m = np + r

мұнда r < n . Бұл жерде m, n, p, r - натурал сандар (тек m n -ға қалдықсыз бөлінген және r = 0 болған жағдай өзгеше) . Мысалы, егер n = 3, ал r = 2 болса, онда m = 3 p + 2. Бұл 3-бөлгенде қалдықта 2-ні беретін сандардың формуласы.

Мысал. 36 421 санын 25 санына бөлгендегі бөлінді мен қалдықты табу керек.

Шешуі. «Бұрыштап» бөлуді орындайық:

3642125 25

¯ 25 1456

114

¯100

142

¯125

171

¯150

Сонымен, бөлінді 1456, ал қалдық 21 болды. (1) теңдігін пайдаланып, 36421 = 25 ∙ 1456 + 21 деп жаза аламыз.

Бөліну белгілері. Кейбір жағдайларда, m натурал санын n натурал санына бөлуді жүргізбей-ақ, « m -ды n -ға қалдықсыз бөлуге бола ма, әлде болмай ма?» деген сұраққа жауап беріледі.

Бұл сұраққа жауапты әр түрлі бөліну белгілері арқылы алуға болады.

Т. 1. 1. Егер әрбір қосылғыш қайсыбір санға бөлінетін болса, онда қосынды да сол санға бөлінеді (қосындының бөлінгіштік белгісі туралы теорема) .

Бірақ, егер әрбір қосылғыш қандай да бір санға бөлінбесе, онда қосынды да сол санға бөлінбейді деп ойламау керек. Мысалы, 37 + 19 қосындысы 4-ке бөлінеді, ал 37 де, 19 да 4-ке бөлінбейді. Алайда, егер бір қосылғыштан басқа қосылғыштардың бәрі қайсыбір санға бөлінсе, онда қосынды сол санға бөлінбейтінін атап өтеміз.

Т. 1. 2. Егер көбейтінді де кемінде бір көбейткіш қайсыбір санға бөлінетін болса, онда көбейтінді де сол санға бөлінеді (көбейтіндінің бөлінгіштік белгісі туралы теорема) .

Мысалы, көбейтуді орындамай-ақ 105 ∙ 48 ∙ 93 ∙ 54 көбейтіндісі 5-ке бөлінеді деп тұжырымдауға болады, өйткені 105 көбейткіш 5-ке бөлінеді.

Т. 1. 3. Натурал сан оның соңғы цифры 2-ге бөлінгенде және тек сонда ғана 2-ге бөлінеді (2-ге бөліну белгісі) .

Т. 1. 4. Натурал сан оның соңғы цифры не 0, не 5 болғанда және тек сонда ғана 5-ке бөлінеді (5-ке бөліну белгісі) .

Т. 1. 5. Натурал сан оның соңғы цифры 0 болғанда және тек сонда ғана 10-ға бөлінеді (10-ға бөліну белгісі) .

Т. 1. 6. Цифрларының саны үштен кем болмайтын натурал сан соңғы екі цифрынан тұратын екіорынды сан 4-ке бөлінгенде және тек сонда ғана 4-ке бөлінеді (4-ке бөліну белгісі) .

Дәлелдеуді бесорынды аbсdе саны үшін жүргіземіз. Сонда аbсdе - а ∙ 1 + b ∙ 1000 + с ∙ 100 + d ∙ 10 + е. 100, 1000 және 1 сандары үшін 4-ке бөлінетін болғандықтан, 10 000 а + 1000 b + 100 с қосындысы да 4-ке бөлінеді. Олай болса, егер а ∙ 10 + с саны 4-ке бөлінетін болса, онда аbсdе саны да 4-ке бөлінеді, егер де 10 d + е саны 4-ке бөлінбейтін болса, онда аbсdе саны да 4-ке бөлінбейді. Мысалы, 15436 саны 4-ке бөлінеді, өйткені 36 саны 4-ке бөлінеді. 372 514 саны 4-ке бөлінбейді, өйткені 14 саны 4-ке бөлінбейді.

Т. 1. 7. Натурал сан оның цифрларының қосындысы 3-ке бөлінгенде және тек сонда ғана 3-ке бөлінеді (3-ке бөліну белгісі) .

Дәлелдеуді төрторынды аbсd саны үшін жүргіземіз. Сонда аbсd = 1000 а + 100 b + 10 с + d = (999 а + а) + (99 b + b ) + (9 с + с ) + d = (999 а + 99 b + 9 с ) + (а + b + с + d) . 9, 99, 999 сандары 3-ке бөлінеді және (999 а + 99 b + 9 с) + ( а + b + с + d ) қосындысы цифрлардың а + b + с + d қосындысы 3-ке бөлінеді және тек сонда ғана 3-ке бөлінеді. Мысалы, 2742 саны 3-ке бөлінеді, өйткені бұл санның цифрларының 2 + 7 + 4 + 2 = 15 қосындысы 3-ке бөлінеді. 17941 саны 3-ке бөлінбейді, өйткені бұл санның цифрларының қосындысы 22, ал 22 саны 3-ке бөлінбейді.

Т. 1. 8. Натурал сан оның цифрларының қосындысы 9-ға бөлгенде және тек сонда ғана 9-ға бөлінеді (9-ға бөліну белгісі) .

Натурал санды жай көбейткіштерге жіктеу.

Егер санның тек екі бөлгіші (санның өзі мен бір) ғана бар болса, онда ол жай сан деп аталады; егер санның екіден көп бөлгіштері бар болса, онда ол құрама сан деп аталады. Солай, 19 жай сан, өйткені оның екі бөлгіші ғана бар: 1 мен 19; 35 сан құрама сан: оның 4 бөлгіші бар: 1, 5, 7, 35. Жай сан 19-ды екі натурал санның көбейтіндісі түрінде бір ғана тәсілмен өрнектеуге болады: 19 = 1 ∙ 19 (көбейткіштертің ретін ескермегенде) ; құрама 35 санын екі натурал санның көбейтіндісі түрінде екі (бірден артық) тәсілмен өрнектеуге болады: 35 = 1 ∙ 35 = 5 ∙ 7. 1 саны жай санға да, құрама санға да жатпайтынын атап өтейік.

Т. 1. 9. Кез келген құрама натурал санды бір ғана тәсілмен жай (қарапайым) көбейткіштерге жіктеуге болады.

Сандарды жай көбейткіштерге жіктегенде бөліну белгілерін пайдаланады да вертикаль сызықтың оң жағында бөлгіштер, ал сол жағында бөлінгіш, оның астында бөліндінің мәні орналасатындай етіп бағаналап жазу қолданылады. Олай, 360 саны үшін тиімді бұл жазылу мынадай болады:

360 2

180 2

90 2

45 3

15 3

5 5

1

Егер санның жай көбейткіштерге жіктелуінде бір а көбейкіші n рет кездесетін болса, қысқаша былай жазады: а ⁿ , яғни а ∙ а ∙ а ∙ . . . ∙ а = а ⁿ . а ⁿ өрнегі - дәреже, а саны - дәреженің негізі, n саны - дәреженің көрсеткіші деп аталады. Сондықтан 360 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 = 2 ³ ∙ 3 ² ∙ 5 деп жазуға болады.

Бірнеше натурал санның ең үлкен ортақ бөлгіші. 72 және 96 сандары берілсін. 72 санының барлық бөлгіштерін жазайық: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. 96 санының барлық бөлгіштерін жазайық: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96. Осы жазылған бөлгіштердің ішінде бірдейлері бар: 1, 2, 3, 4, 6, 8, 12, 24. Бұл сандардың бәрін 72 мен 96 сандарының ортақ бөлгіштері деп, ал олардың ішіндегі ең үлкенін ең үлкен ортақ бөлгіші деп атайды.

Кез келген а мен b берілген натурал сандары үшін ең үлкен ортақ бөлгішті табуға болады. Ол Д ( а, b ) арқылы белгіленеді («Д - а, b » деп оқылады) . Егер а мен b - Д ( а, b ) = 1 болатындай сандар болса, онда а мен b өзара жай сандар деп аталады. Мысалы, 72 мен 35 сандары (олардың әрқайсысы құрама сан болса да) өзара жай сандар.

Бірнеше санның ең үлкен ортақ бөлгішін табу үшін бұл сандарды жай көбейткіштерге жіктеу керек те ең кіші дәрежелерімен алынған ортақ жай көбейткіштердің көбейтіндісін табу керек.

1-мысал, Д (48, 60, 72) -ні табу керек.

Шешуі. 48 = 2 ⁴ ∙ 3; 60 = 2 ² ∙ 3 ∙ 5; 72 = 2 ³ ∙ 3 ² . Олай болса,

Д (48, 60, 72) = 2 ² ∙ 3. Жауабы: Д (48, 60, 72) = 12.

2-мысал, Д (3780, 7056) -ны табу керек.

3780 = 2 ² ∙ 3 ³ ∙ 5 ∙ 7

7056 = 2 ⁴ ∙ 3 ² ∙ 7 ²

Шешуі. 3780 2 7056 2

1890 2 3528 2

945 2 1764 2

315 2 882 2

105 2 441 3

35 2 147 3

7 2 49 7

1 2 7 7

Сонда Д (3780, 7056) = 2 ² ∙ 3 ² ∙ 7, 3780 санының жіктелуінде де, 7056 санының жіктелуіне де енетін жай көбейткіштер (ең кіші дәрежелі) алынған. Жауабы: Д (3780, 7056) = 252.

Бірнеше натурал санның ең кіші ортақ еселігі. 12 мен 18 сандары берілсін. 12-ге еселі сандарды жазайық: 12, 24, 36, 48, 72, . . . 18-ге еселі сандарды жазайық: 18, 36, 54, 72, 90, . . . Жазылған еселік сандардың ішінде бірдейлері бар: 36, 72, . . . Осы сандардаң бәрін 12 мен 18 сандарының ортақ еселіктері деп, ал олардың ішіндегі ең кішісін 12 мен 18 сандарының ең кіші ортақ еселігі деп атайды.

Кез келген а мен b натурал сандарының ең кіші ортақ еселігі осы сияқты анықталады да, ол К ( а, b ) арқылы белгіленеді (оқылуы, «К - а, b ») .

Бірнеше санның ең кіші еселігін табу үшін бұл сандарды жай көбейткіштерге жіктеу керек те барлық алынған жай көбейткіштердің (оларды ең үлкен дәрежесімен алып) көбейтіндісін табу керек.

Мысал. К (3780, 7056) -ны табу керек.

Шешуі. 3780 = 2 ² ∙ 3 ³ ∙ 5 ∙ 7, 7056 = 2 ⁴ ∙ 3 ² ∙ 7 ² . Сонда К (3780, 7056) = 2 ⁴ ∙ 3 ³ ∙ 5 ∙ 7, яғни 3780 мен 7056 сандарының кемінде біреуі жіктелуіне енетін барлық жай көбейткіштер алынған. Сонымен, К (3780, 7056) = 105 840.

Кез келген а мен b натурал сандары үшін

Д ( а, b) ∙ К (а, b) = а b

теңдігі орынды. Егер, дербес жағдайда, а мен b сандары өзара жай, яғни Д ( а, b ) = 1 болса, онда К ( а, b) = а b . Бұл өзара жай екі санның ең кіші ортақ еселігі осы сандардың көбейтіндісіне тең болатынын білдіреді.

Алгебрада әріптерді қолдану. Айнымалылар. Алгебрада сандардың нақтылы қасиеттері көбінесе әріптердің көмегімен жазылады. Мысалы, қосудың орын ауыстырымдылық заңы (қосылғыштардың орындарын ауыстырғаннан қосынды өзгермейді) былай жазылады: а + b = b + а , мұнда а мен b -ның орнына кез келген сандарды қоюға болады: 3 + 5 = 5 + 3; 100 + 3501 = 3501 + 100 және т. с. с. Әріптердің орнына қоятын санды оның мәні деп атайды. Кейбір жағдайларда (мысалы, теңдеулерде) жазылған теңдік орынды болатындай етіп әріптің орнына тек анықталған сандарды ғана қоюға болады. Мысалы, 7 + х = 10 теңдігі тек х = 3 болғанда ғана орынды. Алгебрада қолданылатын әріптерді айнымалылар деп атайды; бұндай атаудың мағынасы әріптің сандық мәнін өзгертуге болатынында: мысалы, а + b = b + а теңдігінде а =3, b - 5 деп, а = 7, b = 19 деп және т. с. с. алуға болады - барлық жағдайларда да теңдік орынды. 7 + х = 10 теңдігінде х = 3 деп, х = 5 деп алуға болады; айырмашылығы - бірінші жағдайда теңдік дұрыс, ал екінші жағдайда теңдік дұрыс емес болуында. Д ( а, b) = 1 теңдігі а мен b айнымалыларының мынадай мәндерінде дұрыс болады: а = 18, b = 25, а = 100, b = 99; а = 13, b = 1000 және т. с. с. Бұл теңдік айнымалылардың келесі мәндерінде дұрыс емес: а = 8, b = 6, а = 25 , b = 150; а = 7, b = 777 және т. с. с.

Бүтін сандар және оларға амалдар қолдану

Жоғарыда байқағанымыздай натурал сан қатары, ноль саны, бірлік ұғымдары адамдардың практикалық қажеттіліктерінен пайда болған. Сондай-ақ сандарға қолданылатын амалдар жөніндегі бастапқы біліміміздің көзі де айналамыздағы нәрселердің арасындағы қатынастар болады.

Теріс емес бүтін сандарға амалдар қолдану нәтижесінде жаңа сан шығады. Бұл амалдар - қосу, азайту, көбейту, және бөлу.

Қосу. Сандарға қолданылатын арифметикалық амалдардың ең оңайы ол сандарды қосу амалы болып табылады. Бұл амал жиындарға қолданылатын операциялардан шыққан. Расында да, ортақ элементтері жоқ, әр түрлі 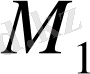және 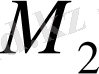екі жиынға тиісті элементтерді бір жиын етіп біріктіргенде, біз жаңа жиынын шығарып аламыз, ал бұл жиын 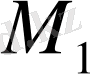және 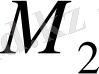жиындарының, тек солардың ғана барлық элементтерінен құралады.

М жиынын берілген М ₁ және М ₂ жиындарының қосындысы деп айтатын боламыз. Сонымен, ортақ элементтері жоқ, берілген М ₁ және М ₂ екі жиынның қосындысы деп сол жиындардың, тек солардың ғана, барлық элементтерінен құралған жаңа жиынды айтамыз.

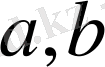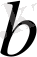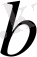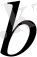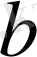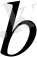Жалпы алғанда, егер М _1, М ₂ және олардың қосындысы М жиындарының тиісті элементтері және болса, онда мен сандарынын санын құрастыру мен сандарын қосу деп аталады, ал саны олардың қосындысы. мен сандары қосылғыштар деп аталады. Мұны былай деп айтуға болады:натурал мен сандарының қосындысы деп мынадай бір жаңа санын айтамыз, ол саны ортақ элементтері болмайтын және қуаттары мен сандарымен өрнектелетін М ₁ және М ₂ жиындарының бірігуі болып табылатын М жиынының қуатын көрсетеді.

Қосуды белгілеп көрсету үшін плюс деп аталатын + таңбасы қолданылады.

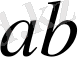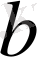Жоғарыда баяндағанымызға қарағанда теріс емес бүтін екі санды қосуды әрқашан да орындауға болады, өйткен берілген екі саның қосындысын санау операциясын қолданып, анықтап айтқанда, санына санының барлық бірліктерін қосып санау арқылы әрқашан да табуға болады.