Тьюринг машиналары

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Жоспар

І. Кіріспе

II. Негізгі бөлім

Тьюринг машина сыртқы және ішкі алфавиттері
Командалары
Пост машинасы
Графиктері

III. Пайдаланған әдебиттер

IV. Қортынды

ТЬЮРИНГ МАШИНАЛАРЫ

Тьюринг машиналары. Сыртқы және ішкі альфавиттер, командалар, бағдарламалар. Тьюринг машинасының жұмысының сипаттамасы.

Егер алгоритм түзу құрылымын қарастырса, онда оларды түзудің үш негізгі типін: сызықтық, тармақталатын, циклдік-ерекшелеуге болады.

Орындаушы командалардың орналасу ретіне қарай бірінен кейін бірін орындайтын алгоритм сызықтық деп аталады.

Орындаушының әрекеті қандай да бір шарттардың орындалу нәтижесімен анықталатын алгоритм тармақталатын деп аталады.

Кейбір жеке командаларды немесе командалар тобын орындағанда бірнеше рет қайталанатын алгоритм циклдік деп аталады.

Көптеген алгоритмдер осы құрылымдардың бәрін өзіне біріктіреді.

Жоғарыда сипатталған алгоритм анықтамалары интуитивті деп аталады, себебі олар адам түсінігіне есепке алады. Бірақ математиканың өзінің есептерін шешу үшін алгоритм ұғымын анықтап алу қажеттігі пайда болды. Алгоритмнің математикалық анықтамасы ХХ ғасырдың отызыншы жылдарының ортасында үш типті модельдерде алынды:

Есептелгіш (рекурсивті) функциялар теориясы;

Ақырлы, ақырсыз автоматтар теориясы;

Марковтың нормалы алгоритмдері.

Бірінен-бірі тәуелсіз тарихи пайда болған бұл тәсілдер, соңыра өзара эквивалентті болып шықты. Алгоритм ұғымын тұрпаттандырудың негізгі мақсаты мынада: әртүрлі математикалық есептердің алгоритмдік шешімділігі мәселесін шешуге жол ашу, яғни есеп шешіміне әкелетін алгоритм құруға бола ма?- деген сұраққа жауап беру. Біз осы мәселенің қойылуын және есептердің алгоритмдік шешімділігі теориясының кейбір нәтижелерін қарастырамыз, бірақ алдымен Пост, Тьюринг машиналары және Марковтың нормалы алгоритмдері мысалында автоматтар теориясындағы алгоритм ұғымын тұлғатандыруды, сонан соң рекурсивті функциялар теориясы негіздерін талқылаймыз.

Өздеріне арналған программалардың қасиеттері туралы әртүрлі тұжырымдауды дәлелдеуге арналған абстракты ( яғни шын емес, тек қиялда ғана бар) Пост пен Тьюринг машиналарын американдық математик Эмил Пост пен ағылшын математигі Аллан Тьюринг бірінен-бірі тәуелсіз (және іс жүзінде бір уақытта) 1936 ж. ұсынды. Бұл машиналар бастапқы мәліметтерді “енгізіп”, программалар орындалғаннан соң нәтижені оқуға мүмкіндік беретін, толығымен анықталған әмбебап орындаушылар болып табылады. Пост машинасы аса танымал емес, бірақ Тьюринг машинасына қарағанда әлдеқайда қарапайым.

Пост машинасы

Пост абстракты машинасы, жазатын немесе оқитын түбіртек арқылы не ен жазылып, не ен оқылатын жеке секцияларға (ұяшықтарға) бөлінген ақырсыз таспа болып табылады.

1. 16. сур. Пост абстракты машинасы.

Таспа (немесе түбіртек) командаға байланысты бір адым солға немесе оңға ауыс қимыл жасай алады. Таспа әрқашан түбіртектің қарсы алдында секция (ұяшық) тұратындай етіп тоқтайды. Абстракты автомат командалары әдетте келесі әрекеттердің бірінен тұрады:

Команда

Таспаның күйі

командадан кейін

Команда: Түбіртектің оңға қозғалуы

Таспаның күйі: ПостТаб11

Команда: Түбіртектің солға қозғалуы

Таспаның күйі: ПостТаб21

Команда: М енін жазу m

Таспаның күйі: ПостТаб31

Команда: С енін өшіру m

Таспаның күйі: ПостТаб41

Команда: Басқаруды беру

Таспаның күйі: ПостТаб51

Команда: Тоқтау стоп n

Таспаның күйі: ПостТаб6

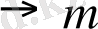
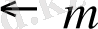
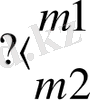
Әрбір команданың өз нөмірі бар: і. Жебеше қозғалыс бағытын көрсетеді. Команданың соңында тұрған екінші j саны жөнелткіш деп аталады. Басқаруды беру командасында екі жөнелткіш болуы мүмкін. Сондықтан да абстракты автомат програмасының екі бірдей қасиеті болуға тиіс:

1) бірінші орында тізімде әрқашан 1-нөмірлі команда тұрады,

екінші орында 2-нөмірлі және т. б;

2) кез келген команданы жөнелткіш әрқашан бағдарлама командаларының тізімінде орналасқан.

Таспаны солға немесе оңға қозғағаннан кейін түбіртек секцияның (бос немесе ен жазылған) күй-жайын оқиды.

Қай секциялар бос, қайсысы белгіленгендігі туралы ақпарат таспа күйін немесе автомат күйін бейнелейді. Автомат программасы деп командалардың ақырлы бос емес тізімін айтады.

Абстракты автомат жұмысы үшін бағдарламаны және бастапқы

күй-жайды, яғни түбіртектің орнын және таспа ұяшықтарының күй-жайын беру керек.

Әрбір қадам сайын бір команда орындалады, сонан соң нөмірі жөнелткіште көрсетілген команда орындала бастайды. Егер бұл команданың екі жөнелткіші болса, және түбіртек астында бос ұяшық болса, онда жоғарғы жөнелткіш нөмірі бар команда орындалады. Егер түбіртек астында ені бар ұяшық болса, онда төменгі жөнелткіш нөмірі бар команда орындалады. Басқаруды беру командасының орындалуы автомат күйін (ендердің ешбірі жойылмайды да қойылмайды, және таспа қозғалыссыз қалады) . Автоматты іске қосқанда мына жағдайдың бірі орын алуы мүмкін:

автомат орындалмайтын команданы (енді бос емес ұяшыққа жазу, бос ұяшықта енді өшіру) орындауға дейін жетті, программаның орындалуы тоқталады, автомат тоқтайды, нәтижесіз тоқтау болады;

автомат стоп командасына дейін жетті, программа орындалды деп есептелінеді, нәтижелі тоқтау болады;

автомат нәтижелі де, нәтижесіз де тоқтауға жетпейді, жұмыс толассыз жүре береді (автомат ілініп қалды) .

Пост машинасының типті программаларының орындалу барысындағы автомат жұмысын қарастырып көрейік. Түбіртектің бастапқы күйі берілсін және бос таспада екі ен салу керек болсын.

Бастапқы күйі

Бастапқы күйі:

: M 2

Бастапқы күйі:

Бастапқы күйі:

: M 4

Бастапқы күйі:

: Стоп 4

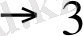
Циклдық үрдісті ұйымдастыру үшін шартты өту командасын қалай пайдалануға болатынын көрсетейік. Таспада қатарынан бірнеше еннен тұратын жазба бар және түбіртек ең шеткі оң жақ еннің үстінде тұрсын. Түбіртекті солға бірінші бос орынға дейін жылжыту қажет.

Бастапқы күйі

Бастапқы күйі: prog2_1

3: стоп 3

Бастапқы күйі: 1-жол

2: п. 1

Бастапқы күйі: 2-жол

2: п. 1

Бастапқы күйі: 3-жол

2: п. 1

Бастапқы күйі: 4-жол

2: п. 3

3: стоп

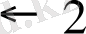
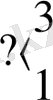
Шартты өту командасы циклдық үрдістерді ұйымдастырудың негізгі құралдарының бірі болып табылады, мысалы бос шаршыдан жоғары орналасқан түбіртектен оң жақ (немесе сол жақ) бірінші енді табу үшін; түбіртектің солынан ( немесе оңынан ) бос шаршы табу, егер ол еннен жоғары орналасқан болса, және т. б.

Осындай, Пост машинасы сияқты қарапайым автоматтарда сандарға әртүрлі амалдар қолдануға болады. Ол үшін абстракты автоматта сандарды көрсету қажет.

Санды автоматты бейнелеу ен салынған секциялар (ұяшықтар) тізбегі арқылы жүзеге асырылады. Бұл тізбек массив деп аталады, ал ондағы секциялар саны- массивтің ұзындығы.

n санын таспада ұзындығы n+1 массиві арқылы беру мақұлданған. Мысалы, 6, 3 және 2 сандары автоматтық бейнелері арқылы суретте былай берілген:

Пост машинасында пайдаланылатын сандарды жазу жүйесі позициялық емес екендігіне көңіл аударайық.

Кез келген санға бір қосудың программасын жасайық. Ол ұшін Пост машинасы үшін мына қасиетке ие болатын программа жазу қажет болады: таспаға жазылған кезкелген п саны үшін программа п+1 санын таспаның кез келген жеріне жазып, нәтижелі тоқтауы керек.

Таспада бір ғана сан жазылған және түбіртек осы санға жататын ен салынған шаршының бірінен жоғары орналасқан болсын. Есепті шешу үшін түбіртекті бірінші бос шаршыға дейін солға (оңға) орын ауыстыруға, сонан соң ен салуға болады.

Программа келесі түрде болуы мүмкін:

1-нұсқа

2-нұсқа

1-нұсқа: 1.

2-нұсқа:

1-нұсқа: 2.

2-нұсқа:

1-нұсқа: 3.

: M 4

2-нұсқа:

M 4

1-нұсқа: 4.

: стоп 4

2-нұсқа:

стоп 4

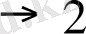
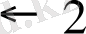
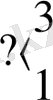
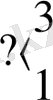
Бастапқы күй-жай санатында кез келген күйі алынуы мүмкін. Онда түбіртек таспаның белгіленген ұяшықтарының бірінде орналасады (яғни сандар жиынтығынан жоғары) . Бұл жағдайда программа күрделілене түседі. Түбіртекті өткен мысалда қарастырылған күйге келтіретін, “санды іздеу блогы”- екі команда пайда болады.

Түбіртек өзіне бірді қосу керек болатын санның сол жағында бірнеше шаршы қашықтықта орналасқан болсын.

Төменде бірді оңына да солына да қосатын программалардың толық мәтіні берілген:

1.: 2.

1.: 3.

1.: 4.

: M 5

1.: 4.

1.: 5.

: Стоп 5

1.: 5.

: M 6

1.: 6.

: Стоп 6

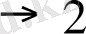
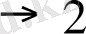
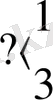
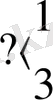
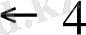
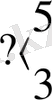
Бірінші жағдайда түбіртекті санның солжақ шеткі еніне орын ауыстырудың қажеті жоқ. Абстракты автомат көмегімен сандық ақпаратты басқаша түрлендіруді де іске асыруға болады. Мысалы, екі санды қосып көрейік. Жалпы қойылымда бұл есеп былай тұжырымдалады: бір-бірінен кезкелген қашықтықта таспаға жазылған а мен в сандарын қосу программасын құрастыру керек. Автоматтың бастапқы күйі суретте көрсетілген:

Программа жазу үшін, мысалы, солжақ массивті оңжақ массивпен бірігіп кеткенше оңға қарай жылжыта беру қерек. Массивті жылжыту ең солжақ енді ең жақын оңжақ бос секцияға (төменде көрсетілген программаның № 1 және №7 командалары) көшіру (өшіру) арқылы жүргізіледі.

Массивтер тұтасқанда (№ 5 және №6 командалар) нәтиже а+в+2 болады. Яғни бір артық енді ( №4 команда) өшіру керек. Соңғы күйінде түбіртек жаңа пайда болған қосындының сол жағында тұр.

C 2

C 5

M 8

10.

1.: 2.

C 2:

4.: 5.

C 5:

7.: 8.

M 8:

10.: 11.

1.: 3.

C 2:

4.: 6.

C 5:

7.: 9.

M 8:

10.: 12.

: стоп

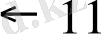
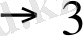
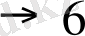
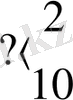
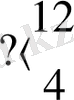
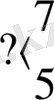
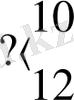
Санның түбіртектің оңында ма, солында ма жатқандығы белгісіз, бостапқы шарттардың аса күрделілігі жағдайында санды іздеудің мынандай принципін қолдануға болады:

Түбіртекті оңға, солға қозғай отырып, түбіртектің бастапқы орыннан қашықтау дәрежесін ен сала белгілей отырып, санды табамыз сонан соң белгілі қосу программасын қолданамыз. Бұл жағдайда түбіртектің сан ендерінің бірінің үстінде тұрған- тұрмағандығы тексеріледі. Егер тұрған болса, онда есеп шешілді. Басқа жағдайда түбіртектің оң жағындағы секцияның және одан кейінгінің бостығы тексеріледі. Егер екеуі де бос болса, онда түбіртек бір адым кейін шегініп, ен салынады, сонан соң осындай амал сол жақтан орындалады да түбіртек белгіленген жолмен оңжаққа қайтып оралады және т. б. түбіртек санға жолыққанға дейін жалғаса береді. Сонан соң жоғарыда қарастырылған программаларды қолдануға болады.

Пост машинасын ЭЕМ-нің қарапайым моделі деп қарауға болады. Шын мәнісінде, ЭЕМ де, Пост машинасында да:

толтырылған немесе толтырылмаған ақпараттың бөлінбейтін тұғырлары (шаршылар- биттер) ;

элементар әрекеттердің шектелген жиынтығы - әрқайсысы бір актыда (адымда) орындалатын командалар-бар.

Екі машина да программа негізінде жұмыс істейді. Дегенмен Пост машинасында ақпарат сызық бойынша орналасады да, бірінен соң бірі оқыла береді, ал ЭЕМ-де ақпаратты адресі бойынша оқуға болады; ЭЕМ командаларының жиынтығы әлде- қайда кең әрі Пост машинасы командаларына қарағанда айқын, т. с. с.

Тьюринг машинасы

Пост машинасына ұқсас, бірақ сәл басқаша жұмыс істейді. Тьюринг машинасы (ТМ) есепші таспадан (ұяшықтарға бөлінген және солынан шектелген, бірақ оңынан емес), оқып және жазатын түбіртектен, таспатартар механизм мен амал атқарушы құрылғыдан тұрады. Құрылғы кейбір ақырлы жиынға (ішкі күй-жай әріппесіне) жататын дискретті күйлерінің бірінде болады. Мұндағы 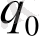- бастапқы күй деп аталады.