Меншіксіз интегралдар: Лаплас түрлендіруі, көп еселі интегралдар, әдістері және теңдеулерге қолданылуы


Жоспар
Кіріспе . . . 3
І бөлім. Интегралдау және меншіксіз интеграл . . . 5
1. 1 Лаплас интегралы . . . 5
1. 2 Екі және үш еселі интегралдар . . . 12
1. 3 Айнымалыны ауыстыру тәсілімен интегралдау . . . 17
1. 4 Лаплас интегралының көмегімен меншіксіз интегралдарды есептеу . . . 20
ІІ бөлім. Меншіксіз интегралдар және оларды теңдеулерге қолдану . . . 22
2. 1 Меншіксіз интегралдар . . . 22
2. 2 Квадрат үшмүшелігі бар өрнектерді меншіксіз интегралдау . . . 24
2. 3 Жоғарғы ретті дифференциалдық теңдеулерді меншіксіз интегралдаудың тәсілдері . . . 252. 4 Меншіксіз интегралдардың қасиеттері . . . 29
Қорытынды . . . 32
Пайдаланылған әдебиеттер тізімі . . . 34
Кіріспе
Алгебралық кеңінен баяндалатын сандар жұйелері мен функциялар, теңсіздіктер сол сияқты көптеген геометриялық тұжырымдарға байланысты мәселелер, проблемалар логикалық жағынан теңдеулер мен теңдеулер жүйелері мен тығыз байланысты болады. Олай болса, теңдеулер мен теңдеулер жүйелерін аталған маңызды мәселелерден мүлде оқшау жалаң қарастыруға болмайды.
Тақырыптың өзектілігі. Математиканы сабағында теңдеулер жүйесін шешудегі интеграл есептердің маңызы зор.
Қазіргі математиканың басқа тарауларда қолданылуы көбінесе математикалық модельдеуге байланысты. Осы ұғымды пайдаланып теңдеулер мен олардың жүйелері математикалық модельдеудегі негізгі құрал ретінде аңықталады.
Сонымен, орта мектепте математикалық білімдер жүйесін оқытуда интеграл есептерді қолдану жөніндегі мәселелерді курс жұмысына лайықты тақырып ретінде таңдау мақсатымен төмендегі дәйектілікке сүйендім, соларды негізге алдым.
Алдымен, интеграл есептер оқушыларды еңбек сүйгіштікке тәрбиелейді. Қарастырылатын мәселерді ең тиімді, ұтымды, пайдалы жақтарынан зерттеуге үйретеді. Атқарылатын жұмыстарға терең, салыстырмалы түрде жан-жақты талдаулар жасай отырып, дұрыс жоспар құруға пәрменді көмегін тигізеді. Орындалған жұмыстардың нәтижелеріне сыншыл көзқараспен қорытындылар жасауға үйретеді. Оқушылардың ойлау жүйесінің, ой қорытындыларының ұтымды логикалық жолымен дамуына кең жол салады. Олай болса, теңдеулер мен теңдеулер жүйелері мектеп математикасын басқа салалары сияқты, оқушылардың ойлау жүйесінің жас жеткіншектерге лайықты дамуына, оларды қоғамға, Отанына пайдалы азамат болып қалыптасуына лайықты пайдасын тигізеді.
Интеграл есептер қолданылатын теңдеулердің дәрежелері бірдей болғанымен, олардың шарттары тиімділікті таңдау тұрғысынан қарағанда өзіндік ерекшеліктері мен оқшаулануы мүмкін.
Курс жұмысының мазмұнын ашуда, әдістемелік мәнін түсіндіруде, теориялық тұжырымдар мен қатар сан-алуан есептер мысалдар оларға сәйкес жаттығулар жүйелері кеңінен қарастырылады. Олар өз кезегінде класта шешілетін, үйде орындалатын және қысқаша бақылау жұмыстары үшін қолданылады.
Осыған байланысты, теориялық материалдарды оқушылардың саналарына қалыптастырудағы жаттығулар жүйелерінің логикалық реттеуіне үлкен маңыз береміз. Сонымен бірге, теңдеулер мен теңдеулер жүйелеріне байланысты жеке тұжырымдарды оқшаулардың өздігінен түсінуіне, баяндай білуіне ерекше мән берілді. Сөйтіп, біз оқушылардың математикалық ойлау жүйесінің дамуына көңіл бөліп отырдық. Онсыз оқушылар санасында математикалық білімдер жүйесін қалыптастыруға, дұрыс практикалық шешімдер қабылдауға болмайды.
Курстық жұмыстың мақсаты: меншіксіз интегралдарға математикалық тұрғыдан жалпы сипаттама беру.
Курстық жұмыстың міндеттері:
- әртүрлі теңдеулерді шешудегі интеграл есептердің ролін анықтау;
- меншіксіз интегралдар мен олардың қолданылуына сипаттама беру;
- меншіксіз интегралдардың басқа интегралдармен сабақтастығын айқындау.
Курстық жұмыстың зерттеу нысаны: математикадағы интеграл есептер.
Зерттеу пәні: математика.
Орта мектепте математикалық білімдер жүйесін оқытуда интеграл есептерді қолдану тақырыбы бойынша жазылған курс жұмысы логикалық жағынан сабақтас екі бөлімнен, қорытындыдан және әдебиеттер тізімінен тұрады.
І бөлім. Интегралдау және меншіксіз интеграл
1. 1 Лаплас интегралы
Нақты айнымалы t-ның
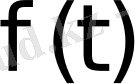 функциясы үшін мына шарттар орындалсын:
функциясы үшін мына шарттар орындалсын:
1) Айнымалы t-ның
 мәндерінде функция мәні
мәндерінде функция мәні
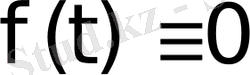 болсын;
болсын;
2) Нақты айнымалы t-ның
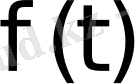 функциясы барлық
функциясы барлық
 мәндерінде үздіксіз болсын.
мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген
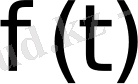 функциясының
функциясының
 өсу дәрежесі шектеулі болсын, яғни барлық
өсу дәрежесі шектеулі болсын, яғни барлық
 мәндерінде
мәндерінде
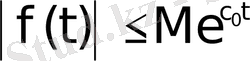 теңсіздігі орындалатындай
теңсіздігі орындалатындай
 және
және
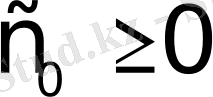 сандары табылсын. Осы шартты қанағаттандыратын
сандары табылсын. Осы шартты қанағаттандыратын
 сандарының ең кішісі
сандарының ең кішісі
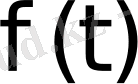 функциясының өсу көрсеткіші деп аталады.
функциясының өсу көрсеткіші деп аталады.
Осы (1) -(3) шарттарды қанағаттандыратын
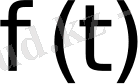 функциясы түпнұсқа деп аталады.
функциясы түпнұсқа деп аталады.
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын
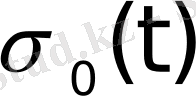 функциясы,
функциясы,
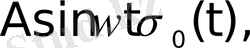
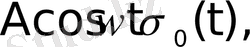
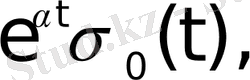
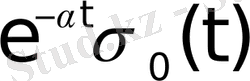
 функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы
 уақыт кезеңі ретінде алуға болады. Сонда t
уақыт кезеңі ретінде алуға болады. Сонда t
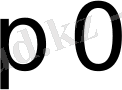 болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген f(t) функциялары үшін орындалады.
Егер осы (1) -(3) шарттардың ең болмағанда біреуі орындалмаса, онда f(t) функциясы түпнұсқа болмайды. Мысалы,
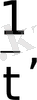
 функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші
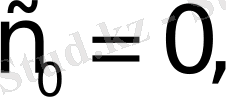 өйткені
өйткені
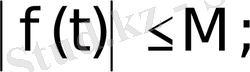
б) Барлық
 түріндегі дәрежелік функциялар. Бұлар үшін
түріндегі дәрежелік функциялар. Бұлар үшін
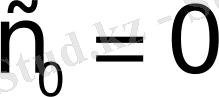 болады. Шынында да
болады. Шынында да
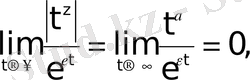
өйткені
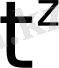 -тің модулі
-тің модулі
 көрсеткіштік функциясына қарағанда баяу өседі.
көрсеткіштік функциясына қарағанда баяу өседі.
Мұндағы
 -қаншалықты болса да аз оң сан.
-қаншалықты болса да аз оң сан.
Осыдан
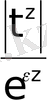 функциясының
функциясының
 аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
 мәндері үшін
мәндері үшін
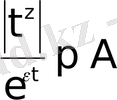 , немесе
, немесе
 теңсіздігі орындалады.
теңсіздігі орындалады.
Мұндағы А-кез-келген оң сан,
 -қаншалықты болса да аз оң сан. Сондықтан
-қаншалықты болса да аз оң сан. Сондықтан
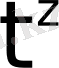 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
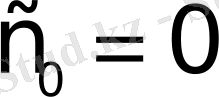 болады.
болады.
Егер
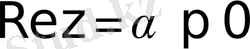 болса, онда
болса, онда
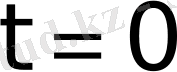 үзіліс нүктесі болады да
үзіліс нүктесі болады да
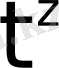 функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Жоғарыдағы
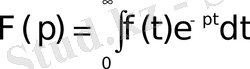 (1)
(1)
теңдігімен анықталған
 комплекс айнымалының
комплекс айнымалының
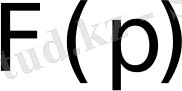 функциясы
функциясы
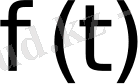 функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
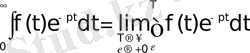 Equation. 3 (2)
Equation. 3 (2)
Мұндағы
 оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
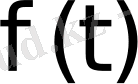 функциясы мен оның
функциясы мен оның
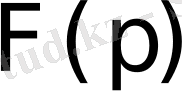 бейнесі арасында сәйкестік орнатылады.
бейнесі арасында сәйкестік орнатылады.
Берілген
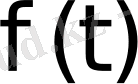 функциясы бойынша оның
функциясы бойынша оның
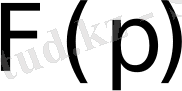 бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
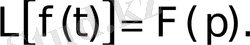 Equation. 3
Equation. 3
Егер
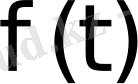 функцияға
функцияға
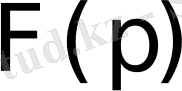 бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
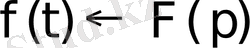 немесе
немесе
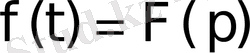 .
.
Егер (2) теңдіктің оң жағындағы шек бар болатын болса, онда Лаплас интегралы жинақталады.
Енді Лаплас бойынша қандай
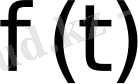 функцияларын түрлендіруге болатынын қарастырайық.
функцияларын түрлендіруге болатынын қарастырайық.
Теорема 1. 1
Егер
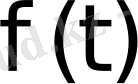 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
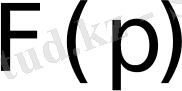 бейнесі
бейнесі
 жарты жазықтығында анықталған.
жарты жазықтығында анықталған.
Мұндағы
 деп
деп
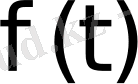 функциясының өсу көрсеткішін ұғамыз.
функциясының өсу көрсеткішін ұғамыз.
Теореманы дәлелдеу үшін р комплекс айнымалысының жазықтығының
 теңсіздігі орындалатын бөлігінде (1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
теңсіздігі орындалатын бөлігінде (1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
Түпнұсқаның (3) шартын пайдаланып мынадай теңсіздіктер аламыз:
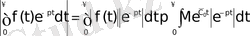
Ал
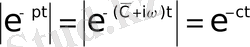 болғандықтан
болғандықтан
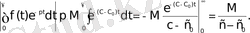 (3)
(3)
Мұндағы
 болғандықтан,
болғандықтан,
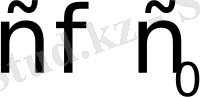
 болса, Лаплас интегралы жинақталады. Сонымен,
болса, Лаплас интегралы жинақталады. Сонымен,
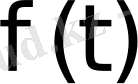 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
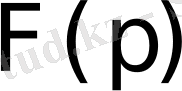 бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
 қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.
қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.

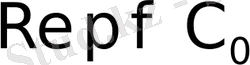
0
 С
С
1-сурет
Осы теоремадан
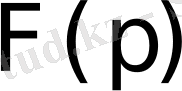 бейнесінің мынадай қасиетін алуға болады.
бейнесінің мынадай қасиетін алуға болады.
Егер (3) теңсіздікте
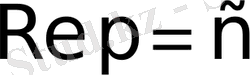 шексіздікке ұмтылса, онда Лаплас нтегралының модулі нолге ұмтылады.
шексіздікке ұмтылса, онда Лаплас нтегралының модулі нолге ұмтылады.
Осыдан
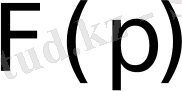 функциясы бейне болса, онда
функциясы бейне болса, онда
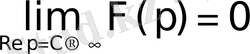 (4)
(4)
болатындығы шығады.
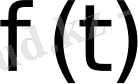 түпнұсқаның
түпнұсқаның
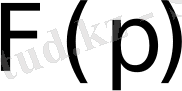 бейнесі
бейнесі
 шарты орындалатын жарты жазықтықта аналитикалық функция болады.
шарты орындалатын жарты жазықтықта аналитикалық функция болады.
Мұндағы
 -түпнұсқаның өсу көрсеткіші.
-түпнұсқаның өсу көрсеткіші.
Анықтама
Мына
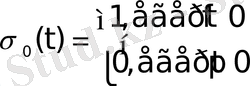 болса,
болса,
шартымен анықталған
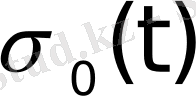 функциясы Хевисайдтың бірлік функциясы деп аталады.
функциясы Хевисайдтың бірлік функциясы деп аталады.
Осы
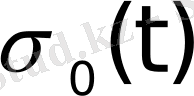 функциясы түпнұсқа болады. Оның өсу көрсеткіші
функциясы түпнұсқа болады. Оның өсу көрсеткіші
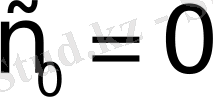 . Бұл функцияның мәні
. Бұл функцияның мәні
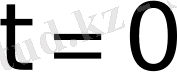 болғанда анықталмаған, өйткені Лаплас интегралын есептегенде
болғанда анықталмаған, өйткені Лаплас интегралын есептегенде
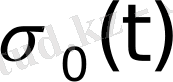 функциясының
функциясының
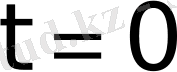 болғанда қандай мән қабылдайтыны ескерілмейді.
болғанда қандай мән қабылдайтыны ескерілмейді.
Дегенмен де,
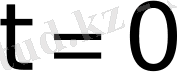 нүктесіндегі мәні үшін әдетте
нүктесіндегі мәні үшін әдетте
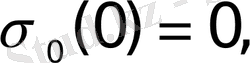
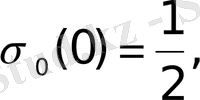 Equation. 3
Equation. 3
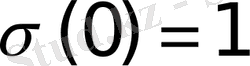 Equation. 3 мәндерін алады.
Equation. 3 мәндерін алады.
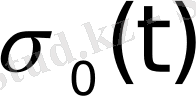
1
t
0
2-сурет
Берілген
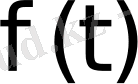 функциясы -
функциясы -
 аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал
аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал
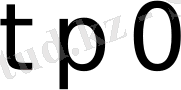 болғанда
болғанда
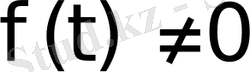 шарты орындалсын. Егер
шарты орындалсын. Егер
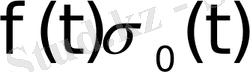 функциясын қарастырсақ, яғни
функциясын қарастырсақ, яғни
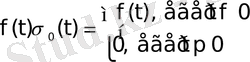 болса, (6)
болса, (6)
онда
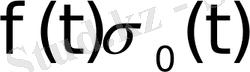 функциясы түпнұсқа болады. Мұндағы
функциясы түпнұсқа болады. Мұндағы
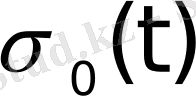 көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта
көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта
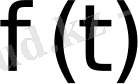 функциясының Лаплас түрлендіруінде
функциясының Лаплас түрлендіруінде
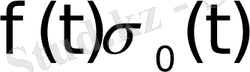 функциясы берілген деп есептеп, оның орнына қысқаша
функциясы берілген деп есептеп, оның орнына қысқаша
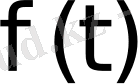 деп жазамыз.
деп жазамыз.
Енді кейбір функциялардың бейнесін анықтама бойынша табу мысалдарын келтірейік.
1 мысал
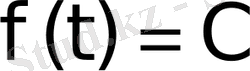 функциясының бейнесін табу керек. Мұндағы
функциясының бейнесін табу керек. Мұндағы
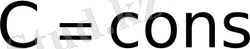 (нақты немесе комплекс сан) .
(нақты немесе комплекс сан) .
Шешуі
Анықтама бойынша
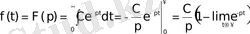
Егер
 Equation. 3 деп алсақ, онда
Equation. 3 деп алсақ, онда
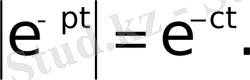 Equation. 3 Сондықтан, егер
Equation. 3 Сондықтан, егер
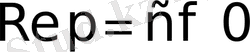 Equation. 3 болса, онда
Equation. 3 болса, онда
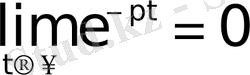 Equation. 3 болады. Нәтижесінде мынадай сәйкестік аламыз:
Equation. 3 болады. Нәтижесінде мынадай сәйкестік аламыз:
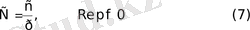
Дербес жағдайда
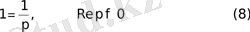
2 мысал
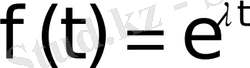 функциясының бейнесін табу керек.
функциясының бейнесін табу керек.
Мұндағы
 (нақты немесе комплекс сан) .
(нақты немесе комплекс сан) .
Шешуі
Егер
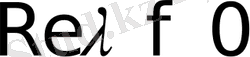 болса, онда
болса, онда
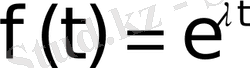 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
 егер
егер
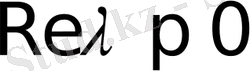 болса, онда
болса, онда
 функциясы шектелген болады да
функциясы шектелген болады да
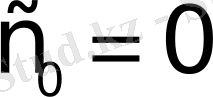 мәнін аламыз. Берілген функцияның Лаплас түрлендіруін жазайық:
мәнін аламыз. Берілген функцияның Лаплас түрлендіруін жазайық:

Мұндағы
 ал
ал
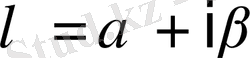 болсын. Олай болса
болсын. Олай болса
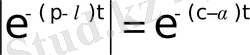 теңдігін аламыз. Осыдан, егер
теңдігін аламыз. Осыдан, егер
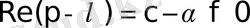 болса, онда
болса, онда
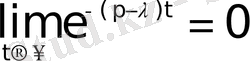 мәні шығады.
мәні шығады.
Нәтижесінде
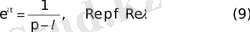
сәйкестігін аламыз.
Дербес жағдайда
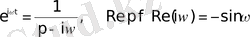 (10)
(10)
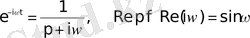 (11)
(11)
Мұндағы ω-кез-келген комплекс сан.
3 мысал
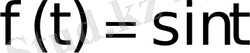 Equation. 3 функциясының бейнесін табу керек.
Equation. 3 функциясының бейнесін табу керек.
Шешуі
 Equation. 3 болғандықтан,
Equation. 3 болғандықтан,
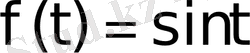 Equation. 3 функциясының өсу көрсеткіші
Equation. 3 функциясының өсу көрсеткіші
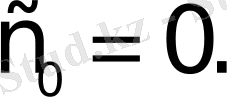 Equation. 3
Equation. 3
Берілген функцияның Лаплас түрлендіруін табайық
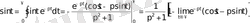
Егер
 болса, онда
болса, онда
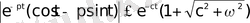
теңсіздігі алынады.
(Мұнда
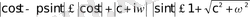 Equation. 3 )
Equation. 3 )
Сонда егер
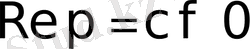 Equation. 3 болса, онда
Equation. 3 болса, онда
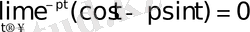 Equation. 3 аламыз.
Equation. 3 аламыз.
Сондықтан

4 мысал
f(t) =cost функциясының бейнесін табу керек.
Шешуі
cost
 1 болғандықтан cost функциясының өсу көрсеткіші с
1 болғандықтан cost функциясының өсу көрсеткіші с
 =0.
=0.
Бұл функцияның Лаплас түрлендіруін жазамыз:

Жақшаның ішіндегі функцияның шегі жоғарыда көрсетілгендей нолге ұмтылады. Сондықтан
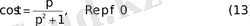
1. 2 Екі және үш еселі интегралдар
Бізге Оху жазықтығының тұйық D аймағында оң таңбалы, үзіліссіз
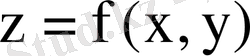 функциясы берілген.
функциясы берілген.
Есеп: Жасаушылары Оху жазықтығына перпендикуляр жоғарғы жағынан
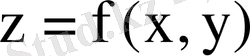 бетімен, төменгі жағынан D аймағымен шенелген цилиндрлік дененің көлемін табу керек. Бұл денені цилиндроид деп атайды. Мұның көлемін табу үшін, оның табаны D -ны
бетімен, төменгі жағынан D аймағымен шенелген цилиндрлік дененің көлемін табу керек. Бұл денені цилиндроид деп атайды. Мұның көлемін табу үшін, оның табаны D -ны
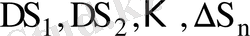 бөліктерге бөлшектеп, әрқайсысынан бір нүкте
бөліктерге бөлшектеп, әрқайсысынан бір нүкте
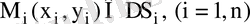 таңдайық. Сонда жуық шамамен
таңдайық. Сонда жуық шамамен
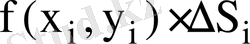 цилиндрдің і - ші бөлігінің көлемін береді (2-сурет) .
цилиндрдің і - ші бөлігінің көлемін береді (2-сурет) .
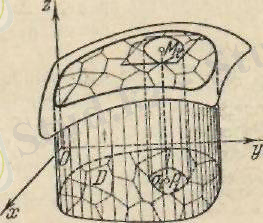
3-сурет
Демек
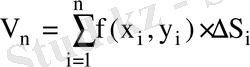 интегралдық қосынды, жуық шамамен бүтін цилиндрдің көлемі. Егер
интегралдық қосынды, жуық шамамен бүтін цилиндрдің көлемі. Егер
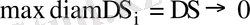 , қосынды V
n
шегін табатын болсақ, онда цилиндроидтың көлемі шығады.
, қосынды V
n
шегін табатын болсақ, онда цилиндроидтың көлемі шығады.
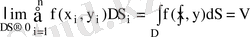 (8. 1)
(8. 1)
Осы шекті D аймағы бойынша
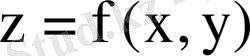 функциясынан алынған екі еселі интеграл деп атайды.
функциясынан алынған екі еселі интеграл деп атайды.
Екі еселі интегралдың негізгі қасиеттері:
1)
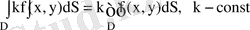
2)
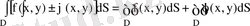
3) Егер D=D 1 ∪D 2 D=D 1 ∪D 2 ≠∅ болса, онда
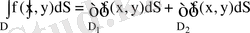
4) Егер D аймағында,
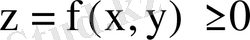 , онда
, онда
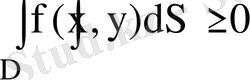
5) Егер D аймағында,
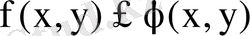 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
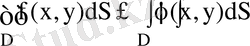
Интегралдау аймағы D мына сызықтармен
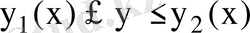
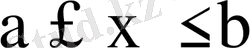 шенелген болсын. Мұндағы
шенелген болсын. Мұндағы
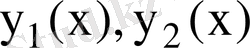
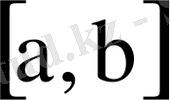 сегментінде бірмәнді, үзіліссіз функциялар. Осы шарттар орындалған жағдайда:
сегментінде бірмәнді, үзіліссіз функциялар. Осы шарттар орындалған жағдайда:
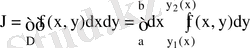 (8. 2)
(8. 2)
Бұл формуланың оң жағындағы интегралды
қайталама
интеграл деп атайды. Егер D аймағы
 ,
,
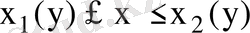 сызықтармен шенелген болса, онда
сызықтармен шенелген болса, онда
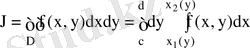 (8. 3)
(8. 3)
Бұл интегралдардың біреуін екіншісімен ауыстыруға болады.
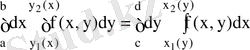
Мысал 1 Интегралдау ретін өзгертіңіз.
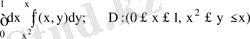
Шешуі
D аймағы
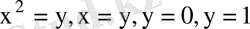 , осыдан
, осыдан
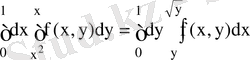 .
.
Мысал 2 Интегралдау ретін өзгертіңіз.
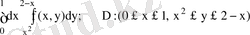
Шешуі D=D 1 +D 2 болғандықтан (3-сурет),
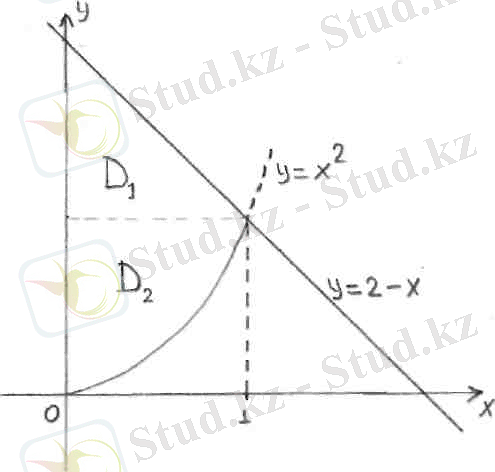
4-сурет
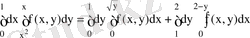
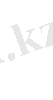
Екі еселі интеграл
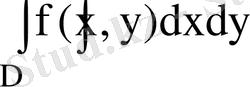 қарастырайық.
қарастырайық.
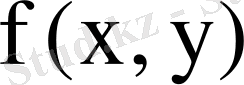 функциясы шенелген тұйық D аймағында үзіліссіз.
функциясы шенелген тұйық D аймағында үзіліссіз.
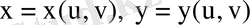 (8. 4)
(8. 4)
формулалары арқылы жаңа
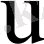 және
және
 аргументтеріне көшіп (8. 4) теңдеулер жүйесінен
аргументтеріне көшіп (8. 4) теңдеулер жүйесінен
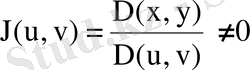 деп есептеп,
деп есептеп,
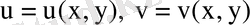 (8. 5)
(8. 5)
функциялары анықталады.
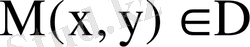 нүктесіне
нүктесіне
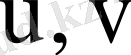 координаттар жазықтығында
координаттар жазықтығында
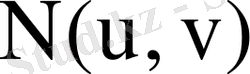 нүктесі сәйкес келеді. Онда (8. 4) формуласындағы функциялардың дербес туындылары бар болады да, мына анықтауыш
нүктесі сәйкес келеді. Онда (8. 4) формуласындағы функциялардың дербес туындылары бар болады да, мына анықтауыш
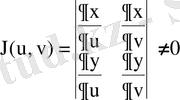 ,
,
сонда
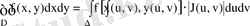 (8. 6)
(8. 6)
теңдігі орындалады.
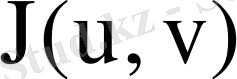 -ны
-ны
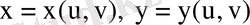 функцияларының Якобинаны деп атайды. ∆ - (8. 4) түрлендіруіндегі D-ның бейнесі.
функцияларының Якобинаны деп атайды. ∆ - (8. 4) түрлендіруіндегі D-ның бейнесі.
Егер (8. 4) формуладан полярлық координаталарға көшетін болсақ, яғни
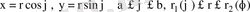 (8. 7)
(8. 7)
деп алсақ, онда, (8. 7) алмастыруының Якобианы
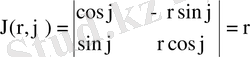
екенін ескеріп,
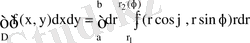 (8. 8)
(8. 8)
теңдігіне келеміз.
Мысал 3
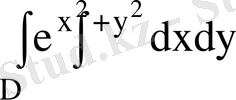 , D - бірінші квадрантта жататын
, D - бірінші квадрантта жататын
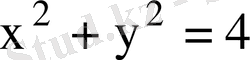 дөңгелегінің бөлігі
дөңгелегінің бөлігі
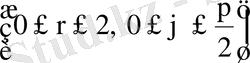 . Осы интегралды есептеу керек.
. Осы интегралды есептеу керек.
Шешуі
 формулаларынан
формулаларынан
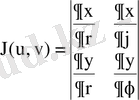 ;
;
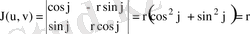 .
.
Сондықтан,
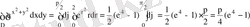 .
.
Мысал 4
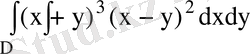 интегралын есепте, егер D:
интегралын есепте, егер D:
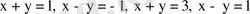 түзулерімен шенелген аймақ болса.
түзулерімен шенелген аймақ болса.
Шешуі
Айталық,
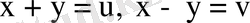 болсын, онда
болсын, онда
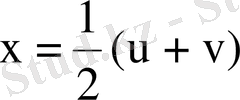 ,
,
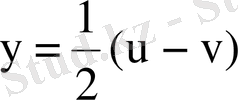 . Ал түрлендіру Якобианы
. Ал түрлендіру Якобианы
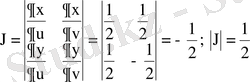 .
.
Сондықтан,
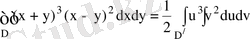 ,
,
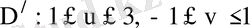
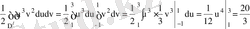 .
.
1. 3 Айнымалыны ауыстыру тәсілімен интегралдау
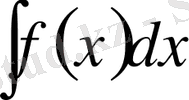 - анықталмаған интегралын қарастырамыз, мұндағы
- анықталмаған интегралын қарастырамыз, мұндағы
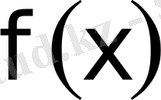
 кесіндісінде үзіліссіз функция. Интеграл астындағы функция «күрделі» болып, яғни интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру ыңғайлы болады, яғни
кесіндісінде үзіліссіз функция. Интеграл астындағы функция «күрделі» болып, яғни интегралдау қиындық келтіреді, сондықтан айнымалыны ауыстыру ыңғайлы болады, яғни
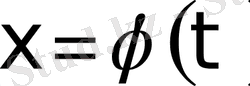 делік, мұндағы
делік, мұндағы
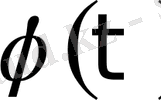 алынатын интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап алынады.
алынатын интегралды кестелік интегралға жеңіл тәсілмен келетіндей таңдап алынады.
Теорема.
Егер
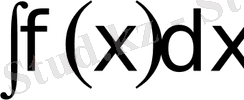 интегралында
интегралында
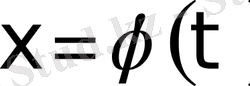 (
(
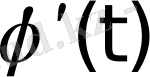 мен
мен
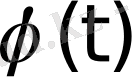 - үзіліссіз функциялар) ауыстыруын алсақ, онда
- үзіліссіз функциялар) ауыстыруын алсақ, онда
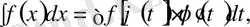 (3)
(3)
формуласы орындалады, яғни жаңа
 интегралын аламыз, ал ол кестелік интегралға оңай келуі мүмкін.
интегралын аламыз, ал ол кестелік интегралға оңай келуі мүмкін.
Дәлелдеу.
Сол жағын
 бойынша, оң жағын
бойынша, оң жағын
 бойынша күрделі функция ретінде дифференциалдаймыз:
бойынша күрделі функция ретінде дифференциалдаймыз:
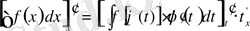 ;
;
 Оң бөлігі мен сол бөлігінің теңдігі теореманың дұрыстығын дәлелдейді.
Оң бөлігі мен сол бөлігінің теңдігі теореманың дұрыстығын дәлелдейді.
Практикалық тәсіл:
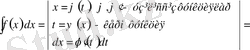
=
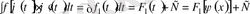 .
.
Алғашқы функцияны тапқаннан кейін ескі айнымалыға қайта ауыстырамыз.
Мысалдар.
1)
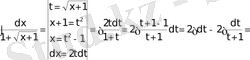
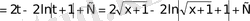 ,
,
2)
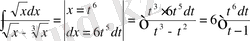 ,
,
(t- 1 ) -ге бөлу арқылы жеңіл интегралданады.
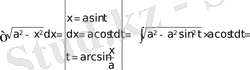
=
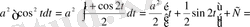
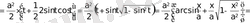
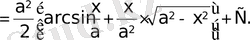
Негізгі интегралдар кестесі
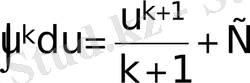 ,
k
≠-1;
,
k
≠-1;
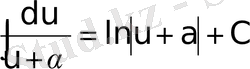 ;
;
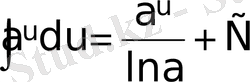 ;
;
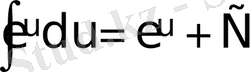 ;
;
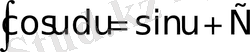 ;
;
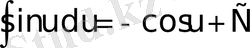 ;
;
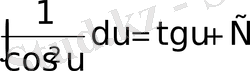 ;
;
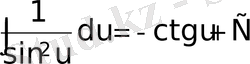 ;
;
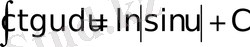 ;
;
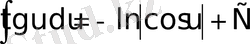 ;
;
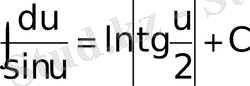 ;
;
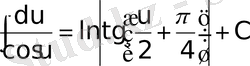 ;
;
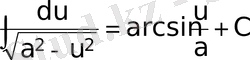 ;
;
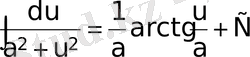 ;
;
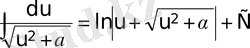 ;
;
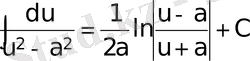 ;
;
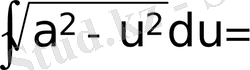
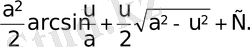
1. 4 Лаплас интегралының көмегімен меншіксіз интегралдарды есептеу
а)
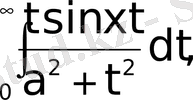 б)
б)
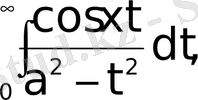 в)
в)
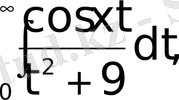
г)
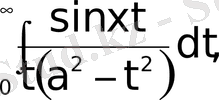 д)
д)
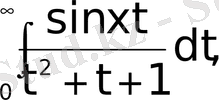 е)
е)
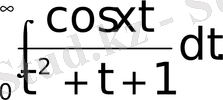
Мына меншіксіз интегралдарды (79) формуланың көмегімен есептеу керек.
а)
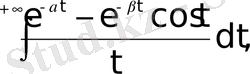
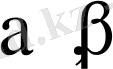 >0
>0
б)
 a>0, b>0
a>0, b>0
 R
R
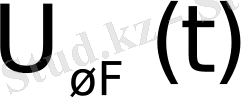
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz