Тригонометриялық теңдеулерді шешу әдістері және элементар тригонометриялық функциялардың графиктері мен интегралдануы


Жоспар
Кіріспе . . . 3
I бөлім. Қарапайым тригонометриялық теңдеулер . . . 5
1. 1 Тригонометриялық теңдеулер . . . 5
1. 2 Жіктеу арқылы шешілетін тригонометриялық теңдеулердің графигі . . . 6
1. 3 Теңбе-тең түрлендірулер арқылы қарапайым түрге келтірілетін тригонометриялық теңдеулер . . . 13
II бөлім. Элементар тригонометриялық функциялар және олардың графиктері . . . 17
2. 1 Кері тригонометриялық функцияға тәуелді теңдеулер . . . 17
2. 2 Тригонометриялық теңдеулердің функциялары . . . 19
2. 3 Тригонометриялық функцияларды интегралдау . . . 26
Қорытынды . . . 32
Пайдаланылған әдебиеттер тізімі . . . 34
Кіріспе
Бүгінгі заман талабына сай мұғалім педагогикалық технологияларды жете меңгерген, жаңа қалыпты педагог талаптарына сай құзіретті тұлға болуы тиіс. Елімізді жедел индустриялық-инновациялық дамыту барысында жаратылыстану-математикалық бағыттағы пәндердің, соның ішінде математика пәні аса үлкен маңызға ие болуын мен математик ретінде жақсы түсінемін. Өйткені қазіргі заманғы ғылымдар математикалық әдістерді қолданады және математика заңдылықтары бойынша дамиды.
Тригонометрия элементтерін адамзат ежелгі замандардан бастап, бұрыштарды өлшеу мұқтаждықтары барысында қолдана бастаған. Тригонометриялық функциялардың қазіргі атаулары ХVI-XVIII ғасырларда пайда болған. Синус сөзі латын тілінен аударғанда «дөңестік деген мағынаны білдіреді, ал косинустағы «ко» қосымшасы латынның complementom-толықтауыш деген мағынаны білдіреді. Осы күнгі қолданылып жүрген sinx және cosx белгілеулері 1739 жылы И. Бернуллидің Л. Эйлерге жазған хатында алғаш рет ұсынылған. Бұл белгілеулерді қазіргі кезеңде кеңінен қолдана бастады.
Қарапайым тригонометриялық теңдеулерді қарастырған кезде олардың түрлері бойынша бөлсе қалай болады және бірнеше шешу жолдары болуы мүмкін бе?- деген сұрақтар туындады.
Курстық жұмысты жазу барысында төмендегідей мақсатты алға қойдым:
- тригонометриялық теңдеулердің түрлерін зерттеп, бірнеше тәсілдерін қарастыру.
Аталған мақсатқа жету үшін төмендегідей міндеттерді алға қойдым:
- тригонометриялық теңдеулердің түрлері туралы материалдар жинақтау, классификациялау;
- түріндегі теңдеуді қарастыру;
- кері тригонометриялық теңдеулерді қарастыру;
- теңдеулер жүйесін қарастыру;
- тригонометриялық теңдеулер түріне сипаттама беру;
- күрделі тригонометриялық теңдеулерді шешуді жинақтау;
- тригонометриялық теңдеулерді түрлері бойынша бөлу;
- тригонометриялық теңдеулері бар есептер жинағын құрастыру.
Курстық орындау барысында математикалық есептеу жұмыстары мен модельдеу, талдау әдісі тәрізді жалпы ғылыми әдістер қолданылды. Бұл әдістердің сипаттамалары ІІ бөлімде баяндалады.
Курстық жұмыстың құрылымы кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
І бөлім. Қарапайым тригонометриялық теңдеулер
1. 1 Тригонометриялық теңдеулер
Екі тригонометриялық функцияның теңдігін қанағаттандыратын аргументтің мәндерін іздеу тригонометриялық теңдеулерді шешуге келтіріледі. Мұндай теңдеулер тек нақты сандар жиынында ғана қарастырылады.
Мысалы,
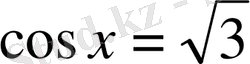 теңдеуінің түбірі жоқ, ал
теңдеуінің түбірі жоқ, ал
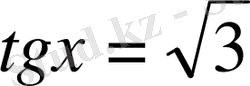 десек,
десек,
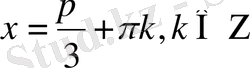 .
.
Тригонометриялық теңдеулерді түрлендіріп
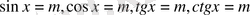 -түріне келтіреді. Бұлардың шешімдері төмендегідей болады:
-түріне келтіреді. Бұлардың шешімдері төмендегідей болады:
- егерболса, ;
- егерболса, ;
- егеркез келген сан болса, ;
- егеркез келген сан болса, .
Тригонометриялық теңдеулер көбінесе негізгі алгебралық функцияларға келтіріліп шешіледі. Мысалы,
1.
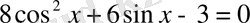 теңдеуді шешу керек.
теңдеуді шешу керек.
 -ті
-ті
 арқылы жазсақ,
арқылы жазсақ,
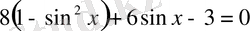 шығады. Бұдан
шығады. Бұдан
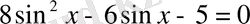
1)
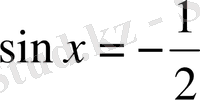 бұдан
бұдан
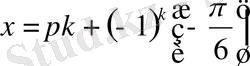 немесе
немесе
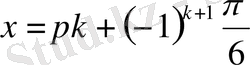
2)
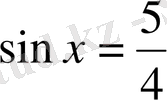 бұл теңдеудің шешуі жоқ, себебі
бұл теңдеудің шешуі жоқ, себебі
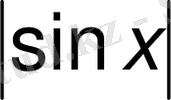 бірден артпауы керек.
бірден артпауы керек.
2.
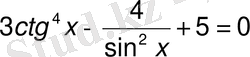 теңдеуді
теңдеуді
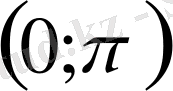 аралығында шешу керек.
аралығында шешу керек.
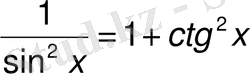 формуласын пайдаланып,
формуласын пайдаланып,
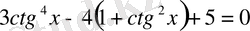 деп жазамыз.
деп жазамыз.
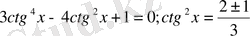
1)
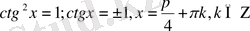
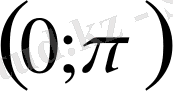 аралығында тек
аралығында тек
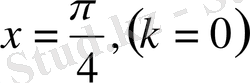 ғана жатады.
ғана жатады.
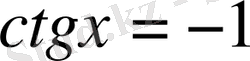 теңдеуін шешсек,
теңдеуін шешсек,
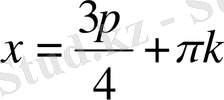 бұнда
бұнда
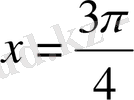 түбірі шартты қанағаттандырады.
түбірі шартты қанағаттандырады.
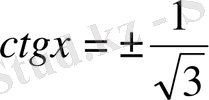
1)
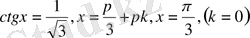 түбірі болады.
түбірі болады.
2)
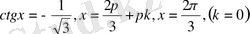
Сонымен, теңдеудің
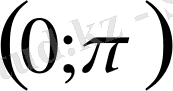 аралығында төрт түбірі болады, олар
аралығында төрт түбірі болады, олар
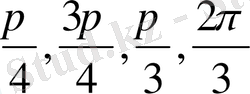 .
.
1. 2 Жіктеу арқылы шешілетін тригонометриялық теңдеулердің графигі
Яғни
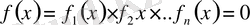 түріне келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге тең болса ғана көбейтінді нөлге тең болады.
түріне келтіретін теңдеулер. Сол белгілі бір бірнеше көбейтінділерден тұрады. Оң бөлігі нөл, сондықтан ең болмағанда бір көбейткіш нөлге тең болса ғана көбейтінді нөлге тең болады.
1.
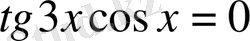 теңдеуді шешіңдер.
(ММЖ)
- мүмкін мәндер жиыны.
теңдеуді шешіңдер.
(ММЖ)
- мүмкін мәндер жиыны.
(ММЖ) тапсақ
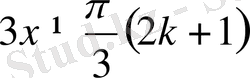 немесе
немесе
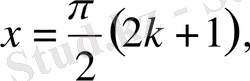
1)
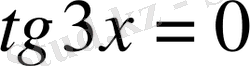 бұдан
бұдан
 яғни
яғни
2)
 бұдан
бұдан
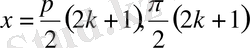 ММЖ
-ға жатпайтынын көрсетейік.
ММЖ
-ға жатпайтынын көрсетейік.
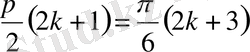
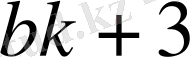
 -
ның қандай мәнінде тақ емес,
ММЖ
жатпайды.
-
ның қандай мәнінде тақ емес,
ММЖ
жатпайды.
2.
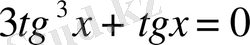
ММЖ
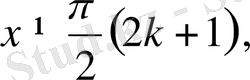
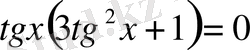
1)
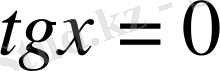 бұдан
бұдан
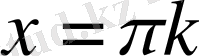
2)
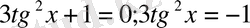 шешімі болмайды, себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
шешімі болмайды, себебі сол бөлігі әруақытта оң сан. Теңдеудің түбірі
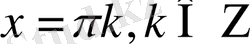 .
.
Қосу формулаларын пайдаланып шешілетін теңдеулер.
Мысалдар:
1.
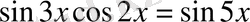 теңдеуін шешіңдер.
теңдеуін шешіңдер.
 -ті
-ті
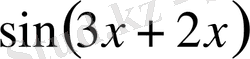 түріне келтіріп аламыз:
түріне келтіріп аламыз:
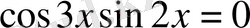
1)
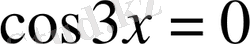 яғни
яғни
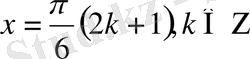
2)
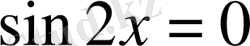 яғни
яғни
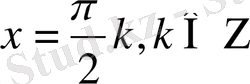
2.
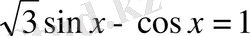 теңдеуін шешіңдер.
теңдеуін шешіңдер.
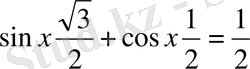 немесе
немесе
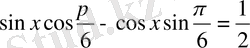
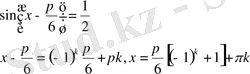
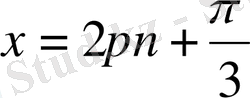 мұндағы
мұндағы
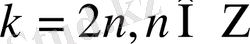
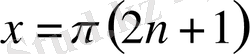 мұндағы
мұндағы
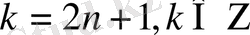 .
.
3.
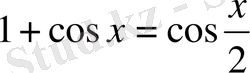 теңдеуді шешіңдер.
теңдеуді шешіңдер.
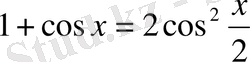 формуласын пайдалансақ
формуласын пайдалансақ
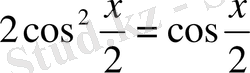 немесе
немесе
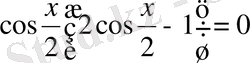
1)
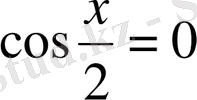 яғни
яғни
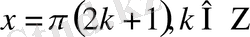
2)
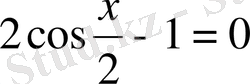
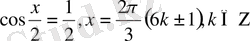 .
.
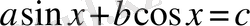
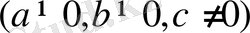 .
.
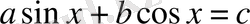
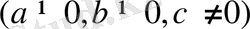 түріндегі теңдеулер. Бұл теңдеулерді
түріндегі теңдеулер. Бұл теңдеулерді
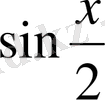 және
және
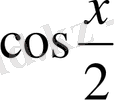 -ге қарағанда біртекті теңдеулерге келтіруге болады. Немесе
-ге қарағанда біртекті теңдеулерге келтіруге болады. Немесе
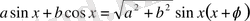 формуласын пайдаланып шешуге болады, мұндағы
формуласын пайдаланып шешуге болады, мұндағы
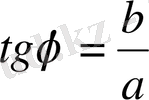 .
.
Мысалы,
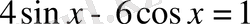 теңдеуді шешу керек. Жарты аргумент функцияларға көшсек,
теңдеуді шешу керек. Жарты аргумент функцияларға көшсек,
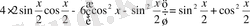
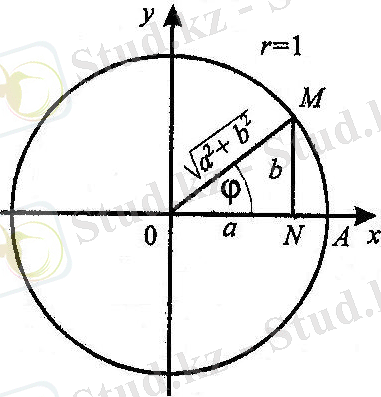 Немесе
Немесе
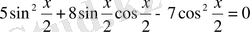 бұл біртекті теңдеу,
бұл біртекті теңдеу,
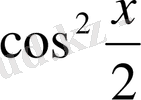 -
ге
-
ге
бөлгенде
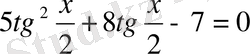 бұдан табатынымыз:
бұдан табатынымыз:
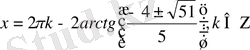
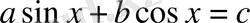 теңдеуінде
теңдеуінде
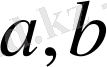 және
және
 -кез келген нақты сандар.
-кез келген нақты сандар.
Егер

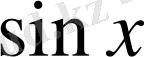 және
және
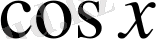 -ке қарағанда біртекті теңдеулер.
-ке қарағанда біртекті теңдеулер.
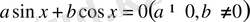 теңдеуі бірінші дәрежелі біртекті теңдеу деп аталады. Бұл теңдеудің екі бөлігін де
теңдеуі бірінші дәрежелі біртекті теңдеу деп аталады. Бұл теңдеудің екі бөлігін де
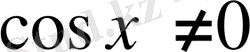 деп бөлсек,
деп бөлсек,
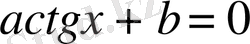 осы теңдеудің түбірін табамыз. Мысалдар:
осы теңдеудің түбірін табамыз. Мысалдар:
1.
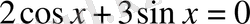 теңдеуін шешу керек.
теңдеуін шешу керек.
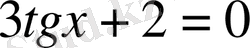 теңдеуімен мәндес.
теңдеуімен мәндес.
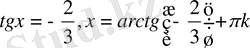 немесе
немесе
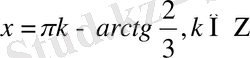
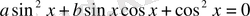 түріндегі теңдеуді екінші дәрежелі
түріндегі теңдеуді екінші дәрежелі
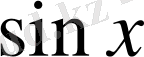 пен
пен
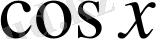 -ке қарағандағы біртекті теңдеу дейді.
-ке қарағандағы біртекті теңдеу дейді.
 -қа бөлсек,
-қа бөлсек,
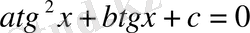 бұлар да мәндес теңдеулер,
бұлар да мәндес теңдеулер,
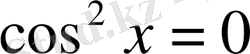 теңдеудің түбірі болмайды.
теңдеудің түбірі болмайды.
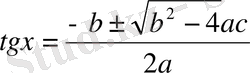 және
және
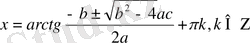 болса теңдеудің шешуі болады. Мысалы:
болса теңдеудің шешуі болады. Мысалы:
1.
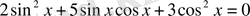 теңдеуін шешу керек.
теңдеуін шешу керек.
 -қа бөліп
-қа бөліп
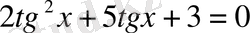 мәндес теңдеу аламыз, бұл теңдеуді шешсек
мәндес теңдеу аламыз, бұл теңдеуді шешсек
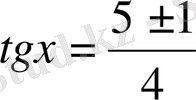
1)
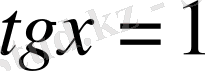 яғни
яғни
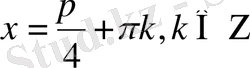
2)
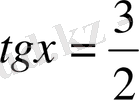 яғни
яғни
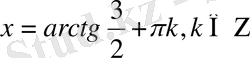
2.
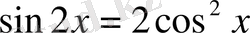
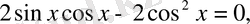
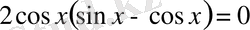
1)
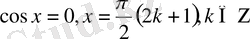
2)
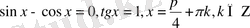
Егер
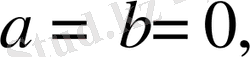 ал
ал
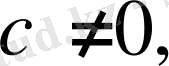 онда теңдеудің мәні болмайды; егер
онда теңдеудің мәні болмайды; егер
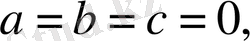 онда
x
-кез келген нақты сан, яғни теңдеу теңдікке айналады. Мысалы
онда
x
-кез келген нақты сан, яғни теңдеу теңдікке айналады. Мысалы
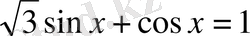 қарастырамыз. Теңдеудің екі жағын 2-ге бөліп,
қарастырамыз. Теңдеудің екі жағын 2-ге бөліп,
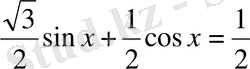 яғни
яғни
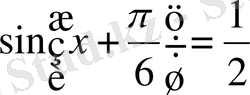 немесе
немесе
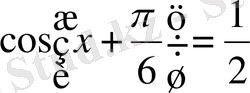 .
.
 теңдеуін төрт тәсілмен шешуге болады. Мысалы, теңдеудің екі жағын да
теңдеуін төрт тәсілмен шешуге болады. Мысалы, теңдеудің екі жағын да
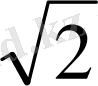 -ге бөліп,
-ге бөліп,
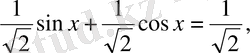
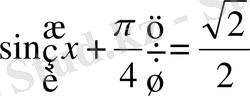 теңдеуін аламыз және т. б. Кез келген коэфиценті бар
теңдеуін аламыз және т. б. Кез келген коэфиценті бар
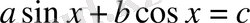 теңдеуін қарастырамыз. Мұндай теңдеулер әр түрлі жолдармен шығарылады.
теңдеуін қарастырамыз. Мұндай теңдеулер әр түрлі жолдармен шығарылады.
1-тәсіл:
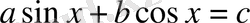 теңдеуін қос бұрыш енгізу әдісі арқылы шешу.
теңдеуін қос бұрыш енгізу әдісі арқылы шешу.
Біз білеміз, егер
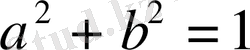 болса,
болса,
 бұрышы болады,
бұрышы болады,
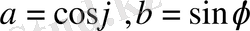 немесе керісінше.
немесе керісінше.
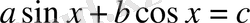 теңдеуін шешу үшін
теңдеуін шешу үшін
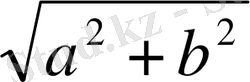 көбейткішін жақша сыртына шығарамыз. Сонда
көбейткішін жақша сыртына шығарамыз. Сонда
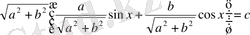 теңдеуін аламыз.
теңдеуін аламыз.
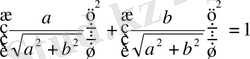 болғандықтан, бірінші
болғандықтан, бірінші
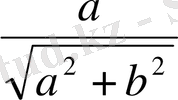 санды кейбір
санды кейбір
 бұрышының косинусы деп қабылдап, ал екінші
бұрышының косинусы деп қабылдап, ал екінші
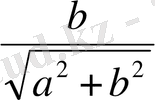 сол
сол
 бұрышының синусымен алмастырып жазамыз, яғни
бұрышының синусымен алмастырып жазамыз, яғни
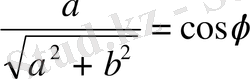 ,
,
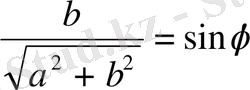 . Мұндай жағдайда теңдеу
. Мұндай жағдайда теңдеу
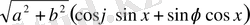 немесе
немесе
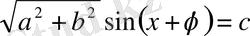 түріне келеді, бұдан
түріне келеді, бұдан
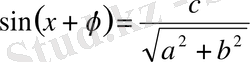 . Бұл теңдеудің шешімі болады, егер
. Бұл теңдеудің шешімі болады, егер
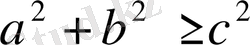 , сонда
, сонда
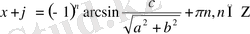 ,
,
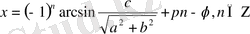 .
.
 бұрышы
бұрышы
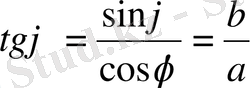 теңдігінен табылады,
теңдігінен табылады,
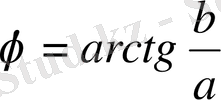 .
.
Жауабы:
 .
.
Қарастырылып өткен тәсіл
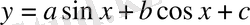 функциясының max, min нүктелерін тапқанда жиі қолданылады.
функциясының max, min нүктелерін тапқанда жиі қолданылады.
Мысалы:
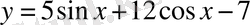 функциясының max, min нүктелерін табу.
функциясының max, min нүктелерін табу.
Шешуі:
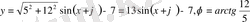 .
.
Максимум
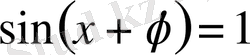 болады, яғни
болады, яғни
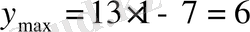 . Ал
. Ал
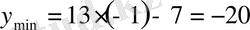 болатынын көру оңай.
болатынын көру оңай.
Жауабы:
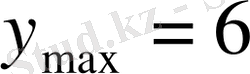 ,
,
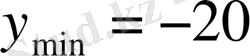 .
.
Қарастырылған тәсіл
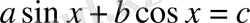 теңдеуінде универсалды болып қарастырылады. Ол сонымен қатар физикада гармониялық тербелістерді қосуда қолданылады.
теңдеуінде универсалды болып қарастырылады. Ол сонымен қатар физикада гармониялық тербелістерді қосуда қолданылады.
2-тәсіл:
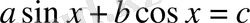 - теңдеуін рационалдау әдісімен шешу.
- теңдеуін рационалдау әдісімен шешу.
Белгілі, егер
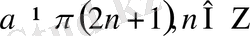 , онда
, онда
 ,
,
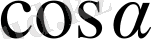 және
және
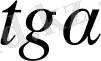 ,
,
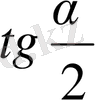 арқылы рационалды өрнектеледі, яғни
арқылы рационалды өрнектеледі, яғни
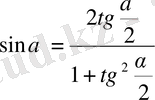 ,
,
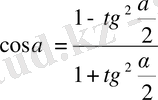 және
және
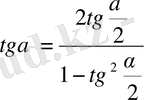 . Рационалдау әдісі мыналардан қорытылады: алмастырудан кейін рационалды теңдеу белгісіз көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
. Рационалдау әдісі мыналардан қорытылады: алмастырудан кейін рационалды теңдеу белгісіз көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз.
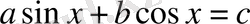 теңдеуін қарастырамыз, бұдан
теңдеуін қарастырамыз, бұдан
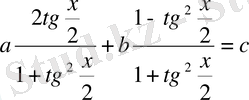 теңдеуін аламыз.
теңдеуін аламыз.
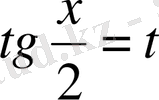 деп алсақ, онда
деп алсақ, онда
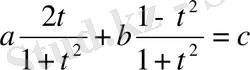 аламыз. Бұл теңдеу- рационалды салыстырмалы
аламыз. Бұл теңдеу- рационалды салыстырмалы
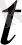 .
.
Теңдеудің екі бөлігін
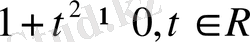 көбейтеміз, сонда
көбейтеміз, сонда
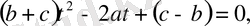
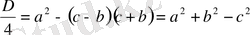 болады.
болады.
 немесе
немесе
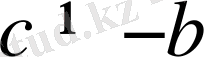 деп көрсек,
деп көрсек,
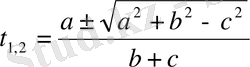 болады.
болады.
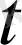 мәні -нақты, егер
мәні -нақты, егер
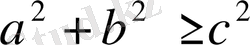 . Егер
. Егер
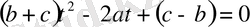 теңдеуінде
теңдеуінде
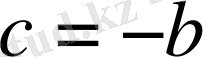 деп алсақ, ендеше ол бірінші дәрежелі теңдеуге айналады:
деп алсақ, ендеше ол бірінші дәрежелі теңдеуге айналады:
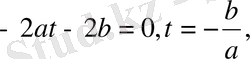 яғни
яғни
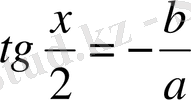 ,
,
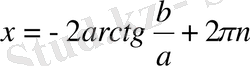 .
.
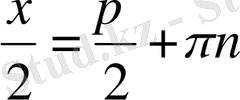 болғанда,
болғанда,
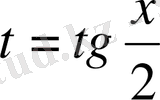 өрнегі көмекші белгісізге мәнін жоғалтады, яғни
өрнегі көмекші белгісізге мәнін жоғалтады, яғни
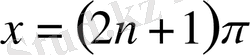 .
.
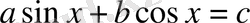 теңдеудің шешімі
теңдеудің шешімі
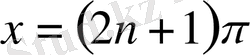 жоғалуы мүмкін.
жоғалуы мүмкін.
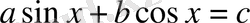 теңдеуді
теңдеуді
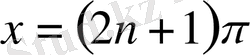 алмастыру арқылы:
алмастыру арқылы:
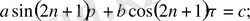
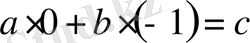 ;
;
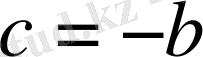 .
.
Мұндай жағдайда
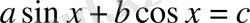 теңдеу
теңдеу
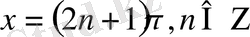 түріндегі шешімдер жиыны көп болады.
түріндегі шешімдер жиыны көп болады.
- Егерболса, ондатеңдеудің шешімі болмайды, теңдеудің нақты түбірлері болмағандықтан.
- Егержәнеболса, ондатеңдеудентабамыз.
- Егер, ондатеңдеудің 2 шешімі бар:және.
1-мысал. Теңдеуді шешіңдер.
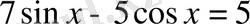
Бұл теңдеуді көмекші бұрыш ендіру арқылы шешуге де болады.
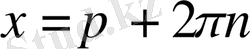 деп алып, төмендегі
деп алып, төмендегі
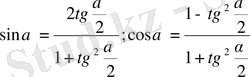 формулалардың көмегімен түрлендірсек,
формулалардың көмегімен түрлендірсек,
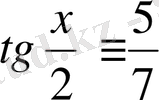 . Бұл арадан
. Бұл арадан
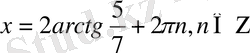 . Енді
. Енді
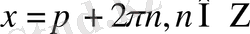 мәні берілген теңдеуді қанағаттандыратынын тексерелік.
мәні берілген теңдеуді қанағаттандыратынын тексерелік.
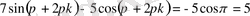
Сонымен теңдеудің шешімі:
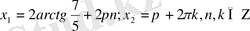
3-тәсіл:
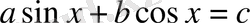 теңдеуін шешу әдісі. Теңдеудің екі бөлігін де квадраттау тәсілімен, біртекті теңдеуін аламыз. Бөгде түбір шығатындықтан, бұл әдіс ең жиі қолданылатын әдіс.
теңдеуін шешу әдісі. Теңдеудің екі бөлігін де квадраттау тәсілімен, біртекті теңдеуін аламыз. Бөгде түбір шығатындықтан, бұл әдіс ең жиі қолданылатын әдіс.
1-мысал. Теңдеуді шешіңдер.
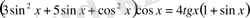
Теңдеуді анықталу облысына
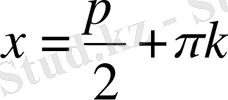 мәні енбейді. Берілген теңдеу тек
мәні енбейді. Берілген теңдеу тек
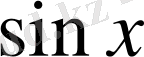 -ке тәуелді, өйткені оны түрлендірсек,
-ке тәуелді, өйткені оны түрлендірсек,
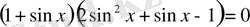 түріндегі теңдеуді аламыз. Анықталу облысын ескерсек,
түріндегі теңдеуді аламыз. Анықталу облысын ескерсек,
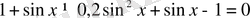 . Теңдеуді
. Теңдеуді
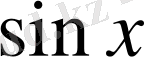 -ке қатысты шешсек, бірінші түбір теңдеудің анықталу облысына енбейді, ал екіншісінен
-ке қатысты шешсек, бірінші түбір теңдеудің анықталу облысына енбейді, ал екіншісінен
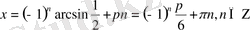 .
.
Барлық тригонометриялық функциялар қатысатын теңдеулерді көбінесе
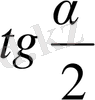 арқылы өрнектеуге болады. Теңдеулерді бұл метод пен шешкенде көбінесе
арқылы өрнектеуге болады. Теңдеулерді бұл метод пен шешкенде көбінесе
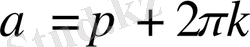 түбірді жоғалтуымыз мүмкін. Сондықтан шешімді тексеру қажет. Бұл методты Эйлер методына алмастыруы деп атайды.
түбірді жоғалтуымыз мүмкін. Сондықтан шешімді тексеру қажет. Бұл методты Эйлер методына алмастыруы деп атайды.
4-тәсіл:
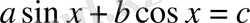 теңдеуін шешу әдісі.
теңдеуін шешу әдісі.
Теңдеуді мына түрде жазып аламыз:
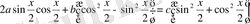 , яғн
, яғн
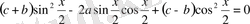 және т. б. түріндегі біртекті теңдеуін аламыз.
және т. б. түріндегі біртекті теңдеуін аламыз.
1. 3 Теңбе-тең түрлендірулер арқылы қарапайым түрге келтірілетін тригонометриялық теңдеулер.
Тигонометриялық теңдеудің сипаты оның құрамындағы тригонометриялық өрнектің қабылдайтын мәндеріне немесе анықталу облысына байланысты. Алгебралық өрнектер сияқты тригонометриялық теңбе-теңдікті құрайтын өрнектерде түрлендіру есептер шешуде аса маңызды роль атқарады. Әсіресе теңдеулер шешуде тригонометриялық теңбе-теңдіктер аклғашқы немесе негізгі ұғым болып саналады. Теңдеулер шешуге өте көп теңбе-теңдіктерден ең қажеттісін таңдап алу-есептің тиімді тәсілдер көмегімен оңай шешілуіне мүмкіндік береді.
Бірнеше мысалдар қарастырайық:
1-мысал. Теңдеуді шешіңдер.
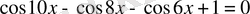
Теңдеуді
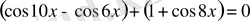 түрінде жазалық. Қосындыға түрлендіріп,
түрінде жазалық. Қосындыға түрлендіріп,
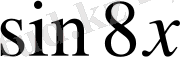 өрнегін қос бұрыштың формуласы бойынша жазсақ, теңдеуді
өрнегін қос бұрыштың формуласы бойынша жазсақ, теңдеуді
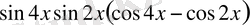 деп жазуға болады. Бұдан
деп жазуға болады. Бұдан
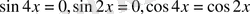 қарапайым теңдеулерге келеді. Бұл арада
қарапайым теңдеулерге келеді. Бұл арада
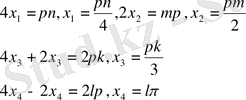
Түбірлерді салыстыра келіп,
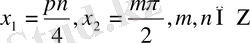 түбірлерінің жалпы түбір екенін байқаймыз.
түбірлерінің жалпы түбір екенін байқаймыз.
2-мысал.
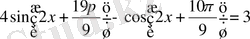 теңдеуді көмекші бұрыш енгізу арқылы шешіңдер. Келтіру формуласының көмегімен
теңдеуді көмекші бұрыш енгізу арқылы шешіңдер. Келтіру формуласының көмегімен
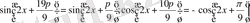 теңдіктерін жазамыз. Бұл арада
теңдіктерін жазамыз. Бұл арада
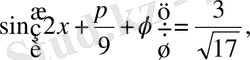 мұндағы
мұндағы
 қарапайым теңдеуін алдық.
қарапайым теңдеуін алдық.

3-мысал.
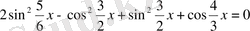 теңдеуді шешіңдер. Дәрежесін төмендету формуласының көмегімен
теңдеуді шешіңдер. Дәрежесін төмендету формуласының көмегімен
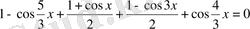
теңдеуді ықшамдаған соң, қосылғыштарды бірге топтап, көбейтіндіге түрлендірсек,
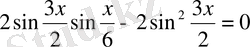 . Бұл арада
. Бұл арада
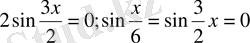 Немесе
Немесе
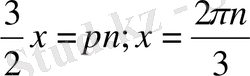 . Екінші теңдеуден
. Екінші теңдеуден
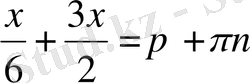 ; Бұл теңдеулерден
; Бұл теңдеулерден
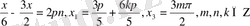 .
.
4-мысал.
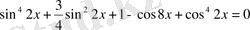 теңдеуін шешіңдер.
теңдеуін шешіңдер.
Бірінші және соңғы қосылғыштарды пайдаланып, толық квадрат алсақ және дәрежесін жоғарылату формуласын пайдалансақ, теңдеу
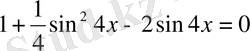 түрге келеді.
түрге келеді.
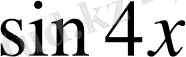 -ке қатысты квадрат теңдеудің түбірлерінен
-ке қатысты квадрат теңдеудің түбірлерінен
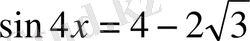 теңдеуін таңдап аламыз. Бұл арадан
теңдеуін таңдап аламыз. Бұл арадан
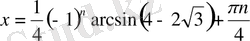 .
.
5- мысал.
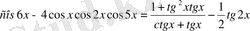 теңдеуді шешіңдер.
теңдеуді шешіңдер.
Теңдеудің шешімі
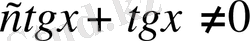 мәндерінде болады.
мәндерінде болады.
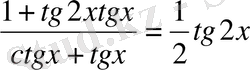 болатынын ескерсек, теңдеу
болатынын ескерсек, теңдеу
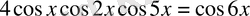 сол жағын қосындыға түрлендірсек, ұқсас мүшелерін біріктіргеннен соң
сол жағын қосындыға түрлендірсек, ұқсас мүшелерін біріктіргеннен соң
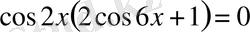 шығады.
шығады.
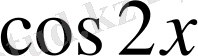 өрнегінің мәні теңдеудің анықталу облысына енбейтіндіктен
өрнегінің мәні теңдеудің анықталу облысына енбейтіндіктен
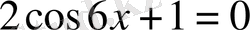 немесе
немесе
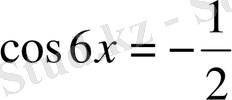 ;
;
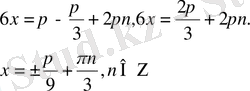
6-мысал.
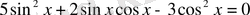 теңдеуді шешіңдер.
теңдеуді шешіңдер.
1-тәсіл. Егер
 , онда
, онда
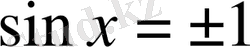 , теңдеу
, теңдеу
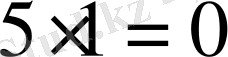 дұрыс емес теңдікке айналады. Ендеше
дұрыс емес теңдікке айналады. Ендеше
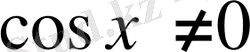 деп аламыз. Теңдеудің екі жағын да
деп аламыз. Теңдеудің екі жағын да
 -ке бөліп,
-ке бөліп,
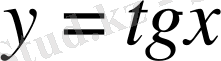 айнымалысын енгіземіз. Онда
айнымалысын енгіземіз. Онда
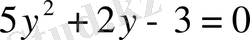 , ал
, ал
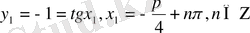 және
және
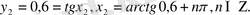
Жауабы:
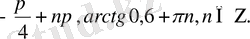
2-тәсіл. Дәрежені төмендету формуласын қолданып, теңдеуді мына түрге келтіреміз
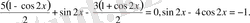
Теңдеудің екі жағын да
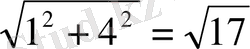 бөліп және қосымша
бөліп және қосымша
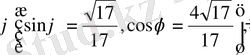 бұрыш енгізу арқылы
бұрыш енгізу арқылы
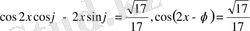 аламыз. Бұдан
аламыз. Бұдан
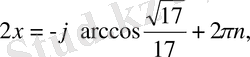
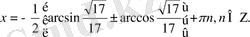
Жауабы:
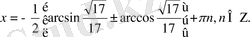
3-тәсіл. Теңдеуді мына түрде жазамыз
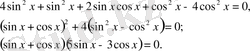
Қалғандары анық.
4-тәсіл. Теңдеуді
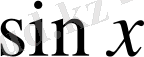 -ке қатысты шешеміз
-ке қатысты шешеміз
 ;
;
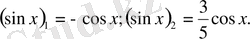
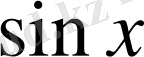 және
және
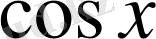 -ты
-ты
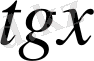 -тың жарты бұрышы арқылы өрнектеу оның ММЖ кішірейтеді және кейбір түбірлерін жойып алады. Қорыта келгенде
-тың жарты бұрышы арқылы өрнектеу оның ММЖ кішірейтеді және кейбір түбірлерін жойып алады. Қорыта келгенде
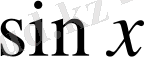 ,
,
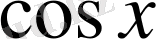 -ты
-ты
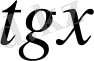 -ң жоғалтады.
-ң жоғалтады.
II бөлім. Элементар тригонометриялық функциялар және олардың графиктері
2. 1 Кері тригонометриялық функцияға тәуелді теңдеулер
Бұл түрге жататын теңдеулердің шешімдерінің саны шектеулі болады. Сондықтан ба оның шешімдерін талдаудың ерекше қиындығы болмайды.
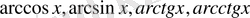 функцияларға тәуелді теңдеу берілсін делік. Ол
функцияларға тәуелді теңдеу берілсін делік. Ол
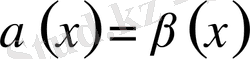 болсын. Мұндағы
болсын. Мұндағы
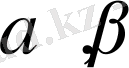 кері тригонометриялық функциялар.
кері тригонометриялық функциялар.
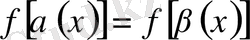 теңдігін жазалық. Соңғы теңдіктен алгебралық теңдеу шығу керек. Бұл теңдеу алғашқы мәндес болмайды. Алгебралық теңдеудің табылған түбірін
x
-тің анықталу облысымен салыстырамыз, қалған түбірлерін берілген теңдеуге қойып тексереміз.
теңдігін жазалық. Соңғы теңдіктен алгебралық теңдеу шығу керек. Бұл теңдеу алғашқы мәндес болмайды. Алгебралық теңдеудің табылған түбірін
x
-тің анықталу облысымен салыстырамыз, қалған түбірлерін берілген теңдеуге қойып тексереміз.
1-мысал.
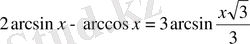 теңдеуді шешіңдер.
теңдеуді шешіңдер.
x -тің анықталу облысын қарастыралық.
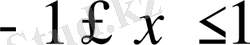 және
және
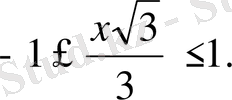 Бұл арадан жалпы алғанда
Бұл арадан жалпы алғанда
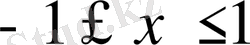 .
.
Теңдеудің екі жағын синустың аргументі деп қараймыз.
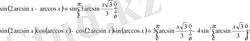
Бұдан әрі
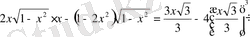
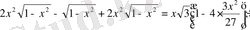
екі жағын квадраттасақ,
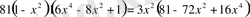 . Түрлендірсек,
. Түрлендірсек,
 бұдан
бұдан
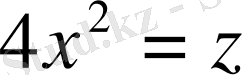 десек, теңдеу
десек, теңдеу
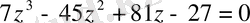 . Осы теңдеуді шешеміз:
. Осы теңдеуді шешеміз:
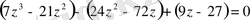
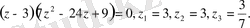 Ал
Ал
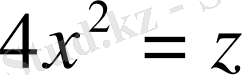 , онда
, онда
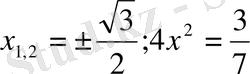 осыдан
осыдан
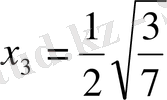 және
және
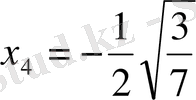 .
x
-тің табылған мәндерінің бәрі оның анықталу облысында жатады. Табылған мәндерді тексерсек,
.
x
-тің табылған мәндерінің бәрі оның анықталу облысында жатады. Табылған мәндерді тексерсек,
1)
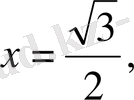 онда
онда
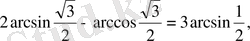 яғни
яғни
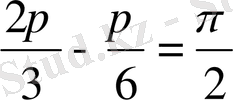 олай болса,
олай болса,
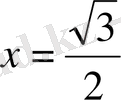 түбір.
түбір.
Тексере келіп, қалған түбірлердің теңдеуді қанағаттандырмайтынын байқаймыз.
2-мысал.
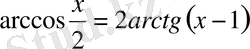 теңдеуді шешіңдер.
теңдеуді шешіңдер.
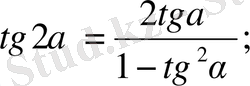
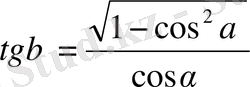 формулаларын пайдаланып, берілген теңдеудің екі жағын тангенс функциясының аргументі ретінде қарастырсақ, берілген теңдеу
формулаларын пайдаланып, берілген теңдеудің екі жағын тангенс функциясының аргументі ретінде қарастырсақ, берілген теңдеу
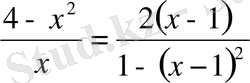 түрінде жазылады.
түрінде жазылады.
Бұдан
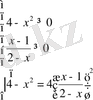
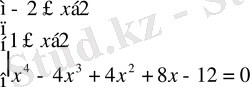 немесе
немесе
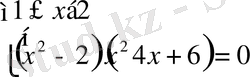 немесе
немесе
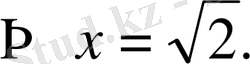
3-мысал.
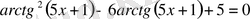 теңдеуді шешіңдер:
теңдеуді шешіңдер:
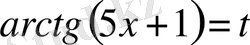 деп белгілесек, онда
деп белгілесек, онда
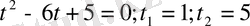
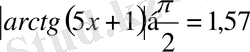 болғандықтан
болғандықтан
1)
 шешім бола алмайды.
шешім бола алмайды.
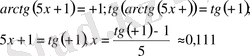 2)
2)
4-мысал. Теңдеуді шешіңдер:
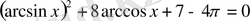
Кері тригонометриялық функциялардың қосындысы туралы теоремаға
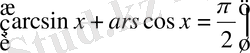 сүйеніп,
сүйеніп,
 -ті
-ті
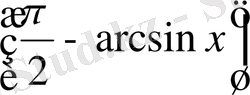 -пен алмастырамыз. Сонда берілген теңдеу
-пен алмастырамыз. Сонда берілген теңдеу
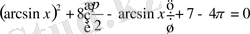 немесе
немесе
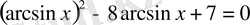 болады. Осыдан
болады. Осыдан
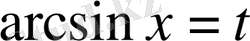 десек
десек
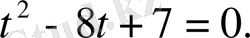
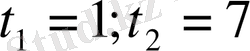
1)
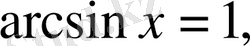
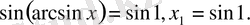
2)
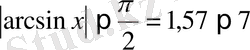 . Олай болса, 7 шешім бола алмайды.
. Олай болса, 7 шешім бола алмайды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz