Сфералық геометрия

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3
I.БӨЛІМ. СФЕРАЛЫҚ ГЕОМЕТРИЯ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .4
1. Сфералық геометрияның пайда болуы ... ... ... ... ... ... ... ... ... ... ... ...4
2. Сфералық геометрияның негізгі ұғымдары ... ... ... ... ... ... ... ... ... ... ...6
2.1. Сфера, үлкен және кіші шеңберлер. ... ... ... ... ... ... ... ... ... ... ... ... ...6
2.2. Сферадағы бұрыш ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .8
2.3. Полюс және полярлар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..8
2.4. Нүктелердің арақашықтығы ... ... ... ... ... ... ... ... ... ... ... ... ... ... .12
2.5. Сфералық геометрия пәні ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 13
II.БӨЛІМ. ҚАШЫҚТЫҚТАН ОҚЫТУ ... ... ... ... ... ... ... ... ... ... ... ... ...15
1. Қашықтықтан оқыту түсінігі және анықтамасы ... ... ... ... ... ... ... ..15
2. Қашықтықтан оқытудың принциптері мен ерекшеліктері ... ... ... ... 17
3. Сфералық геометриядан қашықтықтан оқыту курсы ... ... ... ... ... ... ...20
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 21
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ...22
ҚОСЫМША ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .24

КІРІСПЕ

Менің курстық жұмысымның тақырыбы «Сфералық геометрияны зерттегенде ақпараттық технологияларды қолдану». Индустриалды деп аталған XX ғасырдың орнына ақпараттық деген атаумен XXI ғасыр келгендіктен, менің ойымша, білім беру саласын нығайту қажеттілігі артып келе жатыр. Білім берудің қолданыстағы жүйелері заманауи қоғамның қажеттіліктерін қаншалықты қанағаттандыра алатындығын есепке алу, сонымен қатар жаңа технологиялармен білім алу үшін ұсынылатын баламаларды қарастыру керек. Қазіргі уақытта оқыту жүйесіне электронды оқулықтар мен қашықтықтан оқыту курстары енгізілуде. Міне, осыған байланысты, менің таңдауым да осы тақырып: «Сфералық геометрияны зерттегенде ақпараттық технологияларды қолдану» болды. Жоғарғы оқу орындарындағы геометрияның негізгі курсында сферадағы геометрияға аса назар аударылмайтын болғандықтан, осы курстық жұмысым мен үшін жаңа тақырыппен ұштасады.
Курстық жұмысым екі бөлімнен тұрады. Бірінші бөлімде «сфералық геометрияның» пайда болуы, негізгі түсініктерін қарастырдым.
Ал, екінші бөлім қашықтықтан оқытуға арналды. Оның мазмұны қашықтықтан оқыту түсінігіне, сонымен қатар қашықтықтан оқыту курстарын құрудың мақсаттары мен ерекшеліктерін, олардың артықшылықтары мен кемшіліктерін және негізгі моделдерін қарастырады.
Бұл курстық жұмыстың негізгі мақсаттары:
1. «Сфералық геометрия» тақырыбын оқып-үйрену.
2. «Сфералық геометрияны» оқытатын қашықтықтан оқыту курсын ұйымдастыру.

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Адамар Ж. Элементарная геометрия. Ч.2. М., Учпедгиз, 1958.
2. Андреев А.А. Введение в дистанционное обучение. – М., 1997.
3. Атанасян Л.С. Геометрия. Ч.2. – М.:Просвещение,1987. – 352с.
4. Базылев В.Т. Геометрия. М.:Просвещение,1975.
5. Базылев В.Т. Сборник задач по геометрии. М.:Просвещение,1980. -240с.
6. Десятов Д. К проблеме внедрения дистанционных форм обучения/ Д. Десятов, Б. Преображенский, Т. Толстых // Альма матер: Вестн. высш. шк.. - 2003. - № 4. - С. 13-16.
7. Егоров И.П. Геометрия. – М.:Просвещение,1979. – 256с.
8. Егоров И.П. Основания геометрии. – М.:Просвещение,1984. – 144с.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ..3

I-БӨЛІМ. СФЕРАЛЫҚ
ГЕОМЕТРИЯ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... 4

1. Сфералық геометрияның пайда болуы ... ... ... ... ... ... ... ... ... ... ... ...4

2. Сфералық геометрияның негізгі ұғымдары ... ... ... ... ... ... ... ... ... . ... ..6

2.1. Сфера, үлкен және кіші шеңберлер. ... ... ... ... ... ... ... ... ... ... ... ... ...6

2.2. Сферадағы бұрыш ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .8

2.3. Полюс және полярлар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...8

2.4. Нүктелердің арақашықтығы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..12

2.5. Сфералық геометрия пәні ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 13

II-БӨЛІМ. ҚАШЫҚТЫҚТАН ОҚЫТУ ... ... ... ... ... ... ... ... ... ... .. ... ... .15

1. Қашықтықтан оқыту түсінігі және анықтамасы ... ... ... ... ... ... ... ..15

2. Қашықтықтан оқытудың принциптері мен ерекшеліктері ... ... ... ... 17

3. Сфералық геометриядан қашықтықтан оқыту
курсы ... ... ... ... ... ... ...20

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... .21

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ..22

ҚОСЫМША ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... .24

КІРІСПЕ

Менің курстық жұмысымның тақырыбы Сфералық геометрияны зерттегенде
ақпараттық технологияларды қолдану. Индустриалды деп аталған XX ғасырдың
орнына ақпараттық деген атаумен XXI ғасыр келгендіктен, менің ойымша, білім
беру саласын нығайту қажеттілігі артып келе жатыр. Білім берудің
қолданыстағы жүйелері заманауи қоғамның қажеттіліктерін қаншалықты
қанағаттандыра алатындығын есепке алу, сонымен қатар жаңа технологиялармен
білім алу үшін ұсынылатын баламаларды қарастыру керек. Қазіргі уақытта
оқыту жүйесіне электронды оқулықтар мен қашықтықтан оқыту курстары
енгізілуде. Міне, осыған байланысты, менің таңдауым да осы тақырып:
Сфералық геометрияны зерттегенде ақпараттық технологияларды қолдану
болды. Жоғарғы оқу орындарындағы геометрияның негізгі курсында сферадағы
геометрияға аса назар аударылмайтын болғандықтан, осы курстық жұмысым мен
үшін жаңа тақырыппен ұштасады.
Курстық жұмысым екі бөлімнен тұрады. Бірінші бөлімде сфералық
геометрияның пайда болуы, негізгі түсініктерін қарастырдым.
Ал, екінші бөлім қашықтықтан оқытуға арналды. Оның мазмұны қашықтықтан
оқыту түсінігіне, сонымен қатар қашықтықтан оқыту курстарын құрудың
мақсаттары мен ерекшеліктерін, олардың артықшылықтары мен кемшіліктерін
және негізгі моделдерін қарастырады.
Бұл курстық жұмыстың негізгі мақсаттары:
1. Сфералық геометрия тақырыбын оқып-үйрену.
2. Сфералық геометрияны оқытатын қашықтықтан оқыту курсын
ұйымдастыру.

I -БӨЛІМ. СФЕРАЛЫҚ ГЕОМЕТРИЯ

Сфералық геометрияның пайда болуы

Евклидтік геометриядан ерекшеленетін алғашқы геометрия саласы сфералық
геометрия немесе сферика болды. Сфералық геометрия евклидтің жазықтық пен
кеңістік геометриясына қарағанда кейінірек пайда болған. Жазықтық пен
кеңістік геометриясының пайда болуына жазықтардың, жазық фигуралардың
ауданын өлшеу және формасы әр түрлі үлкен ыдыстар мен қамбалардың
сыйымдылығын, яғни түрлі денелердің көлемдерін өлшеу қажеттілігі түрткі
болады. Ал сфериканың туындауы үшін ең негізгі себеп
жұлдызды аспанды зерттеу болды.
Аспан шырақтарын бақылау ең алғаш рет Ежелгі Египет пен Вавилонда
күнтізбені белгілеу мақсатында жүргізілген. Ал біз египеттікерге
(мысырлықтар) тәулікті 24 сағатқа бөлгендері үшін қарыздармыз.
Вавилондықтардың астрономияны дамытуға қосқан үлестері аса маңызды, әсіресе
олардың күннің тұтылуын анықтауы және VIII ғасырда басталған Набонасар
эрасының алғашқы ғасырларындағы жұлдыздарды бақылаудағы еңбектері. Ежелгі
гректер вавилон астрономиясымен б. ғ. дейінгі IV ғасырда, яғни
планеталардың бастапқы атаулары вавилон үлгісіндегі планета атауларымен
өзгертілген кезде танысқан, бұл планеталардың латынша аудармасы бүгінде
жалпы қабылданған атаулар болып табылады. Птоломейдің Альмагестінде
баяндалған астрономия вавилон астрономдарының, сондай-ақ грек
геометрлерінің дәстүрлерін сіңіріп, бірнеше жылдарға созылған ғылымның даму
нәтижесі болды.
Автолик сферикасы. Осы күнге дейін сақталып қалған ең алғашқы ежелгі
математикалық шығарма, б. ғ. дейінгі IV ғасырдың соңында өмір сүрген
Автоликтің Қозғалып тұрған сфера туралы кітабы. Бұл кітаптың зерттеу
нысаны сол кездерде абстрактілі түрде қарастырылған аспан сферасы болды.
Феодосия сферикасы. Осы күнге дейін ең алғаш болып жеткен сфералық
геометрияның жүйелік шығармасы, б. ғ. дейінгі II-I ғасырларда өмір сүрген
Феодосияның Сферикасы. Феодосия Сферикасы үш кітаптан тұрады, олардың
біріншісі алты анықтама мен 23 сөйлемнен, ал екіншісі бір анықтама мен 23
сөйлемнен, үшіншісі 14 сөйлемнен тұрады.
Феодосияның 1-анықтамасында: Сфера бұл фигураның ішіндегі бір нүктеден
құлайтын барлық түзулер өзара тең болатын бір кеңістік ішіндегі дене
(телесная) фигуралары.
Менелай сферикасы. Анағұрлым жақсы дамыған сфералық геометрияны б.
ғ. дейінгі I ғасырдың соңында өмір сүрген Менелайдың Сфера туралы
трактатынан табуға болады. Менелай шығармасының араб тіліндегі аудармасы
бірнеше нұсқада сақталынып қалынған, олардың ішінде Әбу Наср ибн Ирак пен
Насир әд-Дин ат-Тусидің нұсқалары ең жақсы аударма деп есептеледі. Менелай
сферикасы 39, 21 және 25 сөйлемдерден құралған үш кітаптан тұрады. бірінші
кітаптың кіріспесінде Менелай сфералық үшбұрышқа (үш қабырғалы
фигураға), яғни үлкен дөңгелектердің үш доғасымен, кішкене жарты шеңбермен
дөңгелектермен шектелген беттің бөлігіне және сфералық үшбұрыштың
бұрыштарына сипаттама береді. Егер Феодосия Сферикасының сөйлемдерінің
көбі стереометрияға бағытталған болса, Менелайдың шығармасы Евклид
планиметриясына ұқсас түсіндірілетін сфера бетіндегі геометрияға арналған.
Менелай теоремалары: Сфералық геометрия мен тригонометрияның тарихында
Менелай шығармасының үшінші кітабының 1-сөйлемі ерекше: бұл сөйлемде
бүгінгі күні Менелай теоремасы немесе толық төрттөбелік туралы теорема
деп аталатын теоремасы жазықтық үшін де, сфера үшін де дәлелденеді. Толық
төрт қабырға деп қарама қарсы қабырғаларының жұбы қиылысқанға дейін
жалғасатын жазық немесе сфералық төртбұрыш аталады.
Жирардың сфералық үшбұрыштары пен көпбұрыштарының ауданы. Сфералық
үшбұрыш пен көпбұрыш аудандарының, олардың сфералық үшбұрыштың дефектісі
арқылы өрнектелуі алғаш рет фламанд математигі Альберт Жирардың (1595-1632)
Алгебрадағы жаңалығына қосымша түрінде жарияланған Қайта ашылған
сфералық үшбұрыштар мен көпбұрыштар өлшемі туралы мақалада жарық көрді.
Сфералық тригонометрияның негізгі теоремаларын орта ғасырда Шығыс
ғалымдары ашқан. Косинустар теоремасын IX ғасырдағы Сирия математигі және
астрономы әл-Баттани дәлелдеген. Синустардың сфералық теоремасын Х ғасырдың
орталық азия математиктері мен астрономдары Хорезмнен Ибн Ирак, Хорасандық
Әбу-л-Вафа және Ходженттік әл-Ходжанди бір мезгілде ашқан. Косинустардың
аусымды (екіжақты) теоремасын XIII ғасырда, сфералық тригонометрияның
барлық жүйесіне алғаш рет толығымен түсініктеме берген, Әзірбайжандық
Насир-әд-дин ат-Туси дәлелдеген.

2. Сфералық геометрияның негізгі ұғымдары

2.1. Сфера, үлкен және кіші шеңберлер

Сфера дегеніміз центрі деп аталатын О нүктесінен ρ(О,М)=R қашықтықта
орналасқан кеңістік нүктелерінің геометриялық орны (жиыны). Сфера центрін
оның қандай да бір нүктесімен қосатын кесінді сфераның радиусы деп аталады.
Сфераның екі нүктесін қосатын және де оның центрінен өтетін кесінді
диаметр деп аталады. Бұл анықтамадан барлық радиустар тең және диаметр екі
еселенген радиусқа тең болатыны шығады. Сфераның центрінен өтетін жазықтық
диаметрлік жазықтық деп аталады.
Центрі О, радиусы R болатын сфераны S әріпімен белгілейміз. О
нүктесінен R-ден кем қашықтықта жататын ( жазықтығын алайық. Сонда (
жазықтығы мен S сферасының қиылысуы шеңбер болады. Осы шеңбердің радиусы r
тікбұрышты үшбұрыштың катеті (1-сурет), ол оның гипотенузасы сфераның R
радиусы, ал екінші катеті – сфера центрінен жазықтыққа түсірілген
перпендикуляр h болып табылады. Сондықтан Пифагор теоремасы бойынша r
=.

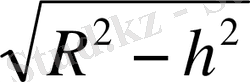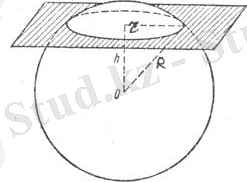
1-сурет

Бұл формула r мәнінің h=0 болғанда r=R теңдігі орындалып r мәні
максималды мәнін қабылдайтындығын көрсетеді, яғни диаметрлік жазықтық болып
табылады. Бұл жағдайда сферадағы шеңбер үлкен шеңбер деп аталады.
Геометриядағы сфералық үлкен шеңберлер жазықтықтағы түзулер рөлін атқарады.
0h, rR болғанда, сферадағы шеңбер кіші шеңбер деп аталады.
Бір түзудің бойында жатпайтын кеңістіктің кез келген үш нүктесінен
жалғыз жазықтық өтеді, онда сфераның диаметралды қарсы болатын екі нүктесі
арқылы жалғыз диаметралды жазықтық жүргізуге болады. Сондықтан, сфераның
диаметралды қарсы болатын екі нүктесі арқылы тек бір ғана үлкен шеңбер
жүргізуге болады (2-сурет). Бұл дерек жазықтықта кез келген екі нүкте
арқылы жалғыз ғана түзу өтеді деген сөйлемнің аналогі. Сфераның диаметралды
қарсы нүктелері арқылы көптеген үлкен шеңберлер жүргізуге болады (3-сурет).
Сфераның кез келген екі диаметрлік жазықтығы оның диаметрі бойынша
қиылысатын болғандықтан, кез келген үлкен шеңбер де сфераның екі
диаметралды қарсы нүктелерінде қиылысады (4-сурет). Осы қасиеттен сфералық
геометрияның жазықтық геометриясындағы екі түзу тек бір ғана нүктеде
қиылысады деген заңдылығына қайшылығын байқаймыз.

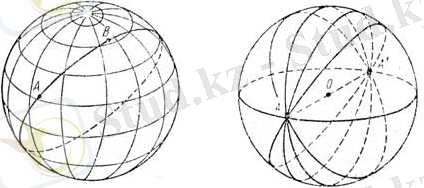
2-сурет
3-сурет

Жазықтық кеңістікті екі облысқа бөлетін болғандықтан, үлкен шеңбер де
сфераны екі облысқа бөледі (2-сурет), бұл облыстар жарты сфера, ал
шеңбердің өзі осы жарты сфералардың жиегі (шеті) деп аталады. Ал,
қиылысатын екі жазықтық кеңістікті төрт облысқа бөлетін болғандықтан, екі
үлкен шеңбер сфераны төрт облысқа бөледі (4-сурет). Соңында, бір нүктеде
қиылысатын үш жазықтық кеңістікті сегіз облысқа бөлетін болғандықтан, бір
нүктеде қиылыспайтын үш үлкен шеңбер сфераны сегіз облысқа бөледі (5-
суретте AB, AC және BC үлкен шеңберлері сфераны бөлетін ABC, ABC(, AB(C,
A(BC, AB(C(, A(BC(, A(B(C, A(B(C( сегіз облыс көрсетілген, бұл ретте
A(,B(,C( нүктелері A,B,C нүктелеріне диаметралды бойынша қарсы нүктелер.
Сол сияқты, ABC және A(B(C(, ABC( және A(B(C, AB(C және A(BC(, A(BC және
AB(C( облыстары жұп-жұбымен диаметрлады қарсы сфералық үшбұрыштар.

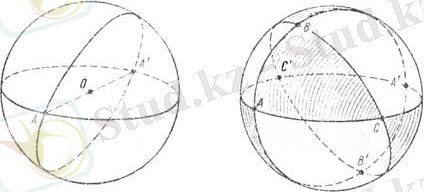
4-сурет
5-сурет

Егер осы қасиеттердің алғашқы екеуі түзу жазықтықты екі облысқа және
қиылысатын екі түзу жазықтықты төрт облысқа бөлетін жазықтықтағы түзулердің
қасиеттеріне ұқсас болса, онда аталған қасиеттердің үшіншісі жазықтықтағы
түзулердің қасиетіне айтарлықтай ұқсас емес, бір нүктеден өтпейтін жұп-
жұбымен қиылысатын үш түзу жазықтықты сегіз емес, жеті бөлікке бөледі (6-
сурет).

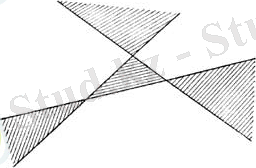
6-сурет

2.2. Сферадағы бұрыш

Кеңістікте қиылысатын екі түзудің арасындағы бұрыш деп олардың қиылысу
нүктесінде осы түзулерге жүргізілген жанамалардың арасындағы бұрышты
айтады. Екі түзу арасындағы бұрыш жалпы жағдайда сферадағы екі үлкен
шеңберлердің арасындағы бұрыш болып табылады. 7-суретте сферадағы үлкен АВ
және АС шеңберлерінің арасындағы BAC бұрышы және осы үлкен шеңберлерге
жүргізілген AX және AY жанамаларының арасындағы XAY бұрышы көрсетілген.

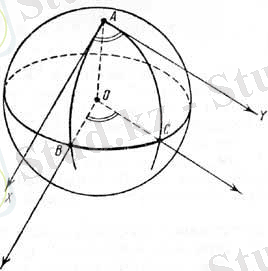
7-сурет.

Сферадағы бұрыштың А төбесінің поляры болып табылатын және осы бұрыштың
қабырғаларын В және С нүктелерінде қиятын үлкен шеңбер жүргізсек, онда ОВ
және ОС сәулелері, сәйкесінше, бұрыштың қабырғаларына жанама болатын АХ
және АҮ сәулелеріне параллель болады (7-сурет). Сондықтан, ВС үлкен
шеңберінің бұрышының ұзындығы (ВАС мен сфера радиусының көбейтіндісіне тең,
яғни сферадағы бұрыш оның қабырғаларында жатқан, сфера радиусына бөлінген
бұрыш төбесімен полярлы түйіндес нүктелерінің арасындағы үлкен шеңбердің
доғасының ұзындығына тең.
Екі жарты шеңбердің әр түрлі ұштарымен түзілген ВАС және ВА'С бұрыштары
бір ВОС бұрышына тең болғандықтан, осы бұрыштар өзара тең және оларды
әрқайсысының аумағы екі үлкен жарты шеңберлер арасындағы бұрыш деп
аталады. Екі үлкен шеңбер екі жарты шеңберлер арасындағы жұп-жұбымен бір
біріне тең төрт бұрышты анықтайды. Қабырғалары басқа бұрыштың
қабырғаларының жалғасы болып табылатын бұрыштар тең және вертикальды
бұрыштар деп аталады (8.а-сурет); ортақ бір қабырғалары бар және қосындысы
жазық бұрышты құрайтын бұрыштар іргелес бұрыштар деп аталады (8.б-сурет).

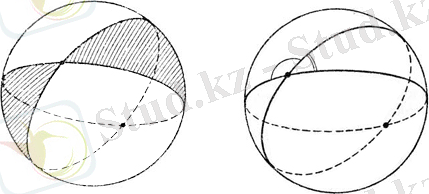
а) б)
8-сурет.

АВ және АС үлкен шеңберлерінің D және Е полюстері АА' айналасында тік
бұрышқа бұрылу арқылы В және С нүктелерінен алынған ВС үлкен шеңберінің
нүктелері болып табылатындықтан, ВС доғасы DE доғасына тең және ВАС бұрышы
сфера радиусына бөлінген DE доғасының ұзындығына тең. D немесе Е
нүктелерінің бірін диаметралды қарсы жатқан D' немесе E' нүктелеріне
алмастыра отырып (9-сурет), ВАС бұрышына іргелес бұрыш аламыз. Осылайша,
екі үлкен шеңберлер арасындағы бұрыш олардың полюстерін жалғастырып тұратын
сфера радиусына бөлінген доғаның ұзындығына тең.

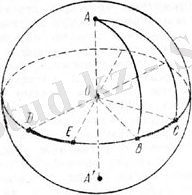
9-сурет.

Диаметрлік жазықтыққа қатысты симметрияда (шағылысуда), осы сферада
жазықтықпен бөлінетін үлкен шеңбердің полюстері бір біріне бейнеленеді,
демек осы жазықтыққа қатысты симметриялы. Осы полюстер арқылы өтетін үлкен
шеңберлер де өздеріне бейнеленеді (10-сурет). Сондықтан, осы үлкен
шеңберлермен және жазықтықпен жасалған үлкен шеңберден құралған бұрыштар
өздерімен іргелес бұрыштарға тең және тік бұрыштар болып табылады.
Осылайша, бірі екіншісінің полюсі арқылы өтетін екі үлкен шеңберлер бір
бірімен тік бұрыш жасап қиылысады. Мұндай үлкен шеңберлерді өзара
перпендикулярлы деп атайды.

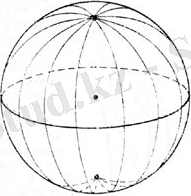
10-сурет.

Керісінше, перпендикуляр екі үлкен шеңбердің бірінде қиылысу нүктесіне
полярлы түрде түйіндес нүктелерді белгілей отырып, бір нүктені аламыз, ол
нүктеге жүргізілген сфера радиусы сферадан екінші үлкен шеңбер жасайтын
диаметрлік жазықтыққа перпендикуляр болады (11-сурет), яғни осы шеңбердің
полюсі болып табылатын нүктені аламыз. Сондықтан, екі перпендикуляр екі
үлкен шеңбердің әрқайсысы екіншісінің полюсі арқылы өтеді.

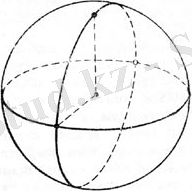
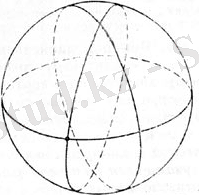
11-сурет 12-сурет.

Осыдан белгілі, екі үлкен шеңбердің қиылысу нүктесінің поляры болып
табылатын үлкен шеңбер екі үлкен шеңберге де перпендикуляр болады, яғни екі
үлкен шеңбердің екеуіне де перпендикуляр болатын тек бір үлкен шеңбер бар
(12-сурет). Салыстыру үшін, жазықтыққа перпендикуляр түзулер параллель
болады, оның үстіне екі параллель түзуге тек бір емес, шексіз көп
перпендикуляр түзулер жүргіуге болатынын ескереміз.

2.3. Полюс және полярлар

Үлкен шеңбер жазықтығына перпендикуляр диаметр сфераны екі диаметрлік
қарсы нүктелерде қияды (13-сурет). Осы екі нүкте үлкен шеңбердің полюстері
деп, ал үлкен шеңбер диаметралды қарсы А және В нүктелерінің поляры деп
аталады. Дербес жағдайда Солтүстік және Оңтүстік полюстер Жер экваторына
сай полюстер болады. Полярдың әрбір нүктесі (демек, үлкен шеңбердің
нүктесі) оның полюстерінің әрқайсысымен полярлы түйіндес полюс деп аталады.
Полярдың барлық нүктелері өз полюсінен 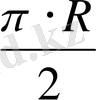(немесе квадрантқа) тең
қашықтыққа орналасатыны түсінікті.

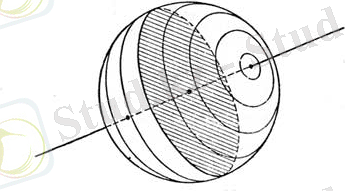
13-сурет

2.4. Нүктелердің арақашықтығы

Екі A,B(S нүктесін алайық және Q осы нүктелерден өтетін үлкен шеңбер
болсын (14-сурет). Q шеңбері, ұштары А және В нүктелерінде жататын өзінің
AMB және ANB доғаларының бірігуі болып табылады. Екі доғаның
ұзындықтарының жарты шеңбердің ұзындығынан қысқасы, А және В нүктелерінің
сфералық арақашықтығы деп аталады және d(A,B) арқылы белгіленеді. Демек,
сфераның S кез келген екі нүктесі үшін d(A,B)≤(r.

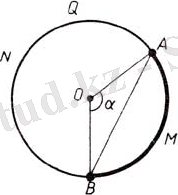
14-сурет.

Егер AMB(Q доғасы жарты шеңберден кем болса, онда d(A,B) осы доғаның
ұзындығы. АМВ доғасын керетін АОВ центрлік бұрыштың шамасын (, ал AB
кесіндісінің ұзындығын ((A,B) деп белгілейік.
d(A,B)=(r
(1)
AOB үшбұрышынан (14-сурет) мынаны табамыз:
((A,B)=2rsin()
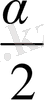(2)
1) , (2) формулалардан келесі формула шығады:
((A,B)=2r sin()
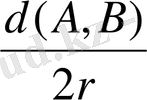(3)

2.5. Сфералық геометрия пәні

Сфералық геометрия сферадағы фигураның кез келген сфералық
қозғалысында сақталып қалатын (өзгермейтін) қасиеттерін зерттейді. Сфераның
қозғалыстарында бір біріне бейнелейтін фигуралар тең фигуралар деп аталады,
тең фигуралардың геометриялық қасиеттері бірдей.

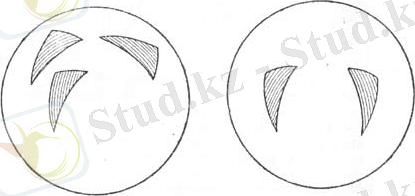
а) б)
15-сурет.
Кейде сфералық геометрия пәніне басқаша анықтама беріледі. Жоғарыда
анықталған қозғалыстардың орнына тек сфераның бұрылыстары (бұру
түрлендіруі) ғана қарастырылады және фигуралардың бұрудағы сақталатын
қасиеттері зерттеледі. Бұруда бір біріне айналатын фигуралар тең деп
айтылады. Ал қозғалыс кезінде бір біріне айналатын, бірақ бұрылыс кезінде
бірікпейтін фигураларды тең деп есептемейді, мұндай фигураларды
симметриялық фигуралар деп атайды. Сонымен, 15.а-суретте тең фигуралар, ал
15.б-суретте симметриялы фигуралар келтірілген.

II-БӨЛІМ. ҚАШЫҚТЫҚТАН ОҚЫТУ

1. Қашықтықтан оқыту түсінігі және анықтамасы

Қашықтықтан оқыту күндізгі және сырттай бөлімдермен қатар, білім
беру процесінде алдыңғы қатарлы дәстүрлі және инновациялық әдістер
негізделген білім беру түрі болып табылады.
Қашықтықтан оқытуда білім ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.