Буль алгебрасы: жалған және елеулі айнымалыларды анықтау теориясы мен бағдарламалық жүзеге асыру


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:
«Астана Медициналық Университеті»АҚ
Медбиофизика курсы мен математика, информатика
Тақырыбы: Буль алгебрасы
Орындаған:
Қабылдаған:
Астана 2012
Мазмұны
1. Математикалық логика . . . 4
2. Математикалық логиканың негізгі функциялары және
Логикалық функцияларының кестесінің мәндері . . . 5
3. Буль функцияларының жалған және елеулі айнымалылары . . . 8
4. Қорытынды . . . 9
5. Пйдаланылған әдебиет . . . 10
Кіріспе
Буль алгебрасы - ішінара реттелген жиынның арнаулы түрі. Жалпы алғанда буль функцияларының жалған және елеулі айнымалыларының дискреттік математикада ойнайтын рөлі өте зор. Бірінші оларды теориялық тұрғыдан қарастырайық. Буль функцияларының жалған және елеулі айнымалылары деп атайды.
Бұл айнымалылардың маңызы өте зор. Мысалы, функция көп айнымалы болса, кейбір айнымалыларын (жалған айнымалыларды) алып тастауға болады. Ол бізге барлық параметрлер бойынша үнемдеуге мүмкіндік береді. Сондықтан осы үнемдеуді жүзеге асыратын программдық пакет құру актуалды мәселе. Бұл жұмыста қойылған мақсат бойынша бірінші теориялық, одан кейін программалық жүзеге асыру жүргізілді. . Буль алгебрасы ағылшын математигі Дж. Бульдің (1815 - 1864) еңбектерінде (1847, 1854) символикалық логиканың аппараты ретінде пайда болды. Кейіннен ол математиканың әр түрлі саласында (ықтималдық теориясы, топология, функционалдық талдау, т. б. ) кеңінен қолданылды.
1. Математикалық логика
Айталық U-{u
1
, и
2
, . . . , и
m
, . . . }
-
айнымалылардың бастапқы алфавиті болсын. Аргументтері E
2
={О, 1} жиынында анықталған және а
i
∈Е
2
(і = 1, 2, . . . , n)
,
егер а
i
∈Е
2
(і = 1, 2, . . . , п) шартын қанағаттандыратын ƒ(u
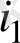 , u
, u
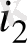 , …, u
, …, u
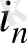 ) функциялары қарастырылады.
) функциялары қарастырылады.
Бұл функциялар логика алгебрасыныц функциялары немесе буль фунщиялары деп аталады. Р 2 арқылы U алфавитінде берілген, сондай-ақ 0 және 1 тұрақтыларын қамтитын барлық логика алгебрасының функциялар жүйесін белгілейміз.
Теорема . х 1 , х 2 , . . . , х n п айнымалыға тәуелді Р 2 жиынындағы барлық
функциялар саны
P
2
(n) -
2
2
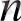 Equation. 3
-
ге тең.
Equation. 3
-
ге тең.
Математикалық логика функцияларының мысалдары:
- ƒ1(x) =0 -тұрақты 0
- ƒ2(x) =1-тұрақты 1;
- ƒ3(x) =x -тепе-тең функция;
- ƒ4(x) =- х -ті жоққа шығару;
- ƒ5(x1, x2) = (x1&x2) - x1мен x2-нің конъюнкциясы (логикалық көбейту) ;
- ƒ6(x1, x2) = (x1∨x2) - x1мен x2-нің дизъюнкциясы (логикальщ қосу) ;
- ƒ6(x1, x2) =Бұл функциялардың мәні.
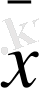
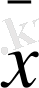
0 0
0 1
0
0
0
1
1
1
0
1
1
1
1
0
1
0
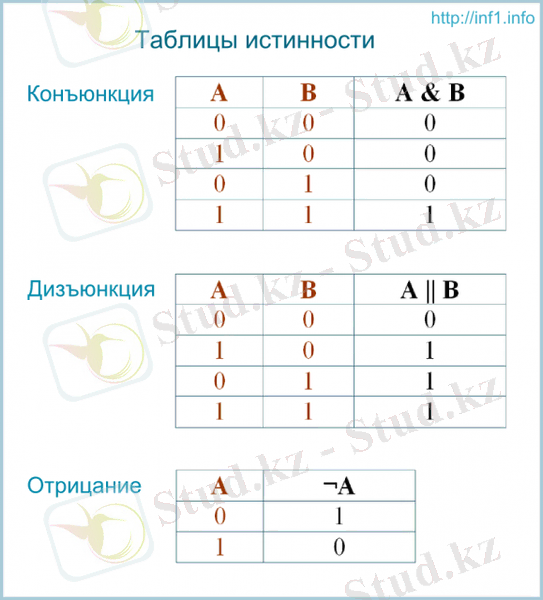
2. Математикалық логиканың негізгі функциялары және
Логикалық функцияларының кестесінің мәндері.
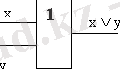
1) ДИЗЪЮНКЦИЯ (Disjunction) -
1) тек екі аргументінің мәні бір мезгілде «жалған» болған кезде ғана мәні «жалған болатын екі айнымалының бүл функциясы. Логикалық «қосу» операциясьша барабар;
2) «немесе»

Кемел дизъюнктивті нормаль қалып
х
 =хσ∨хσ белгілеуін енгізейік, мұндағы σ - нөлге немесе бірге тең параметр.
=хσ∨хσ белгілеуін енгізейік, мұндағы σ - нөлге немесе бірге тең параметр.
x
σ
=
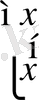
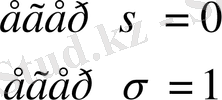
х σ = 1 тек сол жағдайда, егер х = σ болса екендігіне оңай көз жеткізуге болады.
Теорема
(Буль функцияларын айнымалыларға жіктеу туралы) . Әрбір ƒ(х
1
, . . . , x
n
) логика алгебрасының функциясын кез-келген
т(1
 т
т
 п)
үшін келесі түрде беруге болады :
п)
үшін келесі түрде беруге болады :
ƒ (х
1
, . . . , x
m
, x
m+1
, …, x
n
) =
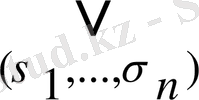 x
1
σ
1
&…& x
m
σ
m
ƒ(σ
1
, …, σ
m
, x
m+1
, …, x
n
),
x
1
σ
1
&…& x
m
σ
m
ƒ(σ
1
, …, σ
m
, x
m+1
, …, x
n
),
(*)
мұнда дизъюнкция х 1 , . . . , х m айньмалыларының барлық мүмкін болатын мәндері бойынша алынады.
Бұл көрініс функцияның х 1 , . . . , х m айнымалылары бойынша жіктелінуі деп аталады.
Салдар ретінде жіктеудің арнайы екі түрін аламыз.
Айнымалы бойынша жіктелу:
ƒ (х
1
, . . . , х
n-1
, х
n
) = х
n
& ƒ (x
1
, …, x
n-1
, 1)
v
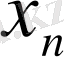 & ƒ(x
1
, …, x
n-1
, 0) .
& ƒ(x
1
, …, x
n-1
, 0) .
ƒ (х 1 , . ., х n-1 , 0) және ƒ(х 1 , . . . , x n-1 , 1) функциялары жіктеудің құрамдас бөліктері деп аталады.
- Барлық айньмалылар бойынша жіктеу:
ƒ (х 1 , . . . , x n ) =
x 1 σ 1 &…& x n σ n ƒ(σ 1 , …, σ n ) .
ƒ (х 1 , . . . , x n ) ≡0 орындалғанда жіктеу келесі түрге айналады
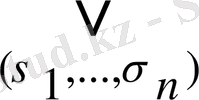 x
1
σ
1
&…& x
n
σ
n
ƒ(σ
1
, …, σ
n
) =
x
1
σ
1
&…& x
n
σ
n
ƒ(σ
1
, …, σ
n
) =
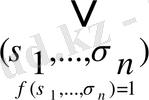 x
1
σ
1
&…& x
n
σ
n
x
1
σ
1
&…& x
n
σ
n
Нәтижесінде
ƒ (х
1
, . . . , x
n
) =
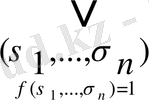 x
1
σ
1
&…& x
n
σ
n
x
1
σ
1
&…& x
n
σ
n
(**)
екендігін аламыз.
Мұндай жіктелу кемел дизъюнктивті нормалъ қалып деп аталады (кемел д. н. ф. ) .
2) КОНЪЮНКЦИЯ (лат. conjunctіo - одақ, байланыс) - логикалық байланымдар, екі пікірдің бірігуінен логикалық “және” жалғауы арқылы пікір құратын логикалық операция (символдық жазылуы: ALB) . Осылай құрылған күрделі пікір оған енетін барлық пікірлер ақиқат болғанда және тек сол жағдайда ақиқат, ал қалған жағдайлардың бәрінде жалған болады.
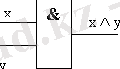
3) ИНВЕРСИЯ - цифрлық сигналдар үшін логикалық терістеу амалын (“емес”) орындайтын электрондық элемент. Сонымен қатар инвертор мәлімет өңдейтін және тасымалдайтын компьютер құрылғыларында электр сигналдарын қалыптастырып күшейтеді. Әдетте, интегралдық сұлбалар құрамында болып, транзисторлық элементтерден тұрады. Потенциалдық және импульстік инверторлар болып ажыратылады. Потенциалдық инверторде кірісіндегі кернеудің жоғары деңгейі шығысында төменгі деңгейге түрленеді және керісінше. Оның кіріс сигналы мен шығыс сигналының арасындағы байланыс логикалық “емес” функциясына сәйкес келеді. Импульстік инверторде кірісіне сигнал келген сәтте оның шығысында полярлығы кірісіндегіге қарама-қарсы сигнал қалыптасады. Инвертор компьютерлердің логикалық элементтерінің негізгілерінің бірі болып табылады. Интегралдық сұлбаларда инвертор өзіндік тәуелсіз міндет атқармай, күрделі логикалық сұлбалардың құрамына кіретін қарапайым элемент қызметін атқарады.
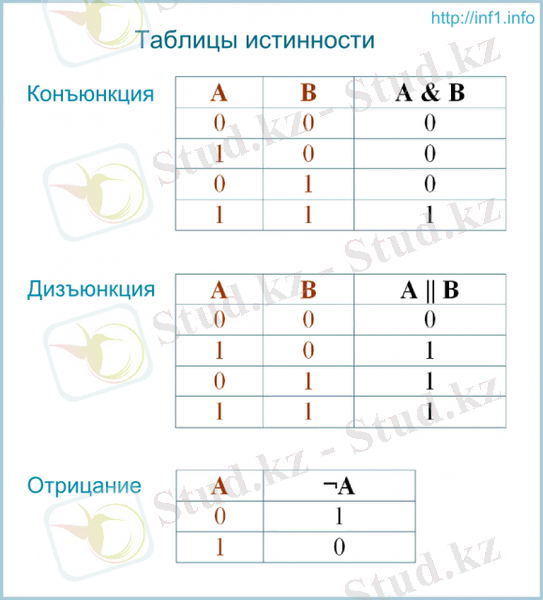
Ұғыну үшін:
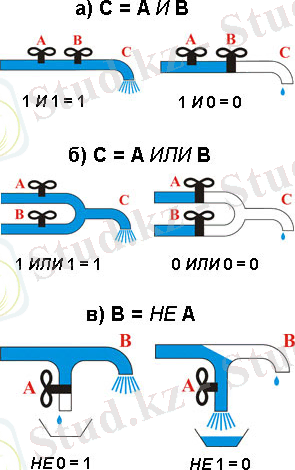
Математикалық логиканың функциялары:
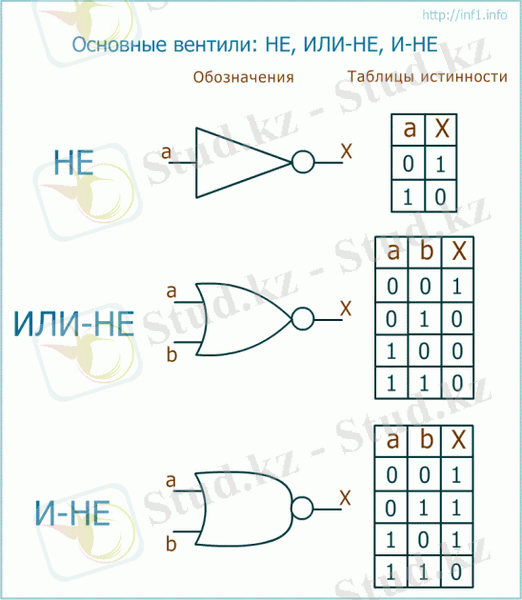
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz