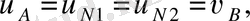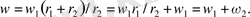Тісті берілістер теориясы және жобалау негіздері: эвольвентті ілініс, күштердің өзгерісі және дәлдік


МАЗМҰНЫ
Кіріспе
- Тісті берілістер
- Тісті берілістер теориясының негіздері
- Эвольвентті іліністің қасиеттері
- Үстемелеу коэффициенті және тістің профилі бойымен күштің өзгеруі
- Тісті берілістің дәлдігі.
- Тістердің істен шығуы және олардың жұмыс істеу қабілеттілігі
Пайдаланылған әдебиеттер
КІРІСПЕ
Тісті беріліс деп, екі қозғалмалы тісті буындары қозғалмайтын буынымен айналмалы немесе ілгерлемелі жұп құратын, үш буынды механизмді айтамыз (тісті беріліс деп қозғалысты, қозғалыс моментін біліктер арасында беру үшін қозғалыстың бір түрін екінші түрге өзгертетін тісті ілінісуді айтады) . Берілістің тісті буыны дөңгелек, сектор немесе рейка болуы мүмкін. Тісті берілістер аыналмалы қозғалыстарды немесе айналмалы қозғалысты ілгерлемелі қозғалысқа түрлендіру үшін қолданылады.
Тісті іліністер жоғарғы кинематикалық жұптарды құрайды, өйткені теория бойынша тістер сызықтың бойымен немесе нүктелермен жанасады. Жұптағы тісті дөңгелектердің кішісін шестерня деп, ал үлкенін - дөңгелек деп атайды. Диаметрі шексіз үлкен тісті доңғалақтың секторын тісті рейка деп атайды.
Тісті берілістер механикалық берілістердің ең көптараған түрлерінің бірі және ол машина жасаудың барлық салаларында, дербес жағдайда металл кесуші білдектерде, автомобильдерде, тракторлерде, ауылшаруашылық машиналарда және т. б. ; аспаптар жасауда, сағаттық өндірісте және б. Тісті берілістердің мұндай кең таралуы жобалау және тісті дөңгелектерді дайындау технологиясы бағыттарында үлкен ғылыми-зерттеу жұмыстарын жүргізуді және бұл мәселеде жан-жақты стандарттауды талап етеді.
- Тісті берілістер
Тісті беріліс деп, екі қозғалмалы тісті буындары қозғалмайтын буынымен айналмалы немесе ілгерлемелі жұп құратын, үш буынды механизмді айтамыз ( тісті беріліс деп қозғалысты, қозғалыс моментін біліктер арасында беру үшін қозғалыстың бір түрін екінші түрге өзгертетін тісті ілінісуді айтады) . Берілістің тісті буыны дөңгелек, сектор немесе рейка болуы мүмкін. Тісті берілістер аыналмалы қозғалыстарды немесе айналмалы қозғалысты ілгерлемелі қозғалысқа түрлендіру үшін қолданылады.
Осы жерде және мұнан да кейін, тісті берілістерге қатысты, терминдер, анықтамалар, белгідеулер 16530-83 МЕСТ «Тісті берілістер», 16531-83 МЕСТ «Цилиндірлі тісті берілістер» және 19325-73 МЕСТ «Конусты тісті берілістер» стандарттарына сәйкес келеді.
Тісті іліністер жоғарғы кинематикалық жұптарды құрайды, өйткені теория бойынша тістер сызықтың бойымен немесе нүктелермен жанасады. Жұптағы тісті дөңгелектердің кішісін шестерня деп, ал үлкенін - дөңгелек деп атайды. Диаметрі шексіз үлкен тісті доңғалақтың секторын тісті рейка деп атайды.
Тісті берілістерді көптеген белгілеріне қатысты сұрыптауға болады: білік өстерінің орналасуына (параллель, қиылысатын, айқасатын және өстері сәйкес келетін) ; жұмыс істеу жағдайларына (жабық - майлы ваннада жұмыс істейтін және ашық - құрғақ жұмыс істейтін немесе оқтын-оқтын майланып тұратын) ; сатысына (бір сатылы, көп сатылы), дөңгелектердің өз-ара орналасуларына (ішкі және сыртқы іліністі) ; біліктердің айналу жіліктерінің өзгеруіне (төмендететін, жоғарлататын) ; тіс кесілетін беттерінің пішіндеріне (целиндрлі, конусты) ; доңғалақтардың шеңберлік жылдамдықтарына (баяу жүргіш - жылдамдығы 3 м/с дейінгі, орташа жылдамдықты - жылдамдығы 15 м/с дейінгі, жылдамжүргіш - жылдамдығы 15 м/с жоғары) ; доңғалақ бетіне тістердің орналасуларына (түзу тістілер, қиғаш тістілер, қисық сызықты шеврон тістілер) ; тістердің профильдерінің формасына (эвольвентті, шеңбер доғасымен шектелген, циклоидты) байланысты жіктеледі.
Сонымен қатар иілгіш тісті доңғалақты берілістер де бар, оларды толқынды деп атайды.
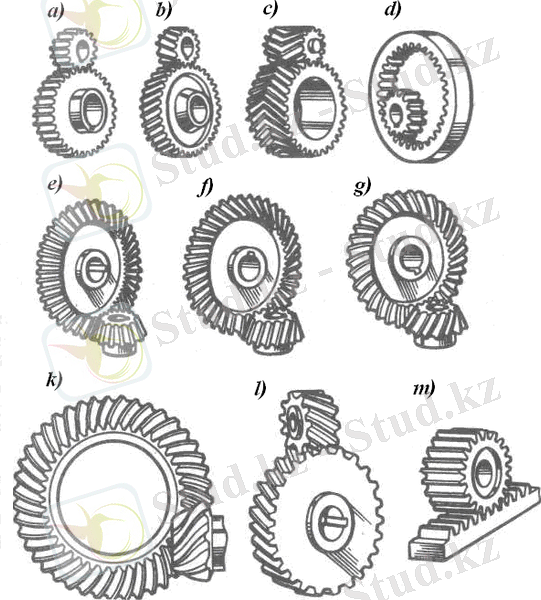
Тісті берілістердің негізгі түрлері (1 - сурет) : өстері параллель: а - цилиндрлі түзу тісті, b - цилиндрлі қиғаш тісті, c - шевронды, d - ішкі ілініспен; өстері қиылысқан: e - конусты түзу тісті; f - конусты тангенсалды тісті, g - конусты қиғаш тісті; өстері айқасқан: h -гипоидті, k - винтті, l - тісті-рейкалы түзу тісті.
Өстері
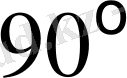 бұрышпен орналасқан тісті берілістер
ортогоналды
деп аталады.
бұрышпен орналасқан тісті берілістер
ортогоналды
деп аталады.
Тісті берілістердің артықшылықтары: тісті берілістер көмегімен өте үлкен қуат беруге болады (ондаған мың кВт) және басқа берілістерге қарағанда ықшамды, габариті шағын келеді, басқа берілістерге қарағанда біліктерге және тіректерге аз күш түседі, тісті берілістер өте шыдамды келеді, пайдалы әсер коэффициенті жоғары (бір сатылы редукторлар үшін 0, 97…0, 98), жылдамдығы үлкен (150 м/с-ке дейін) және беріліс санының диапозоны кеңірек (бірнеше жүздеген) .
Тісті берілістердің кемшіліктеріне мыналар жатады: жоғары дәлдікті берілісті дайындаудың күрделігі; дойындау мен жинаудың дәлдіктерінің жеткіліксіздігінен жұмыс барысында шудың көбейуі, жетектегі біліктің айналу жиілігін сатысыз реттеудің мүмкін еместігі және қатаңдығы өте жоғары болғандықтан динамикалық күштерді қабылдау қабілеттілігінің нашарлығы.
Тісті берілістер механикалық берілістердің ең көптараған түрлерінің бірі және ол машина жасаудың барлық салаларында, дербес жағдайда металл кесуші білдектерде, автомобильдерде, тракторлерде, ауылшаруашылық машиналарда және т. б. ; аспаптар жасауда, сағаттық өндірісте және б. Тісті берілістердің мұндай кең таралуы жобалау және тісті дөңгелектерді дайындау технологиясы бағыттарында үлкен ғылыми-зерттеу жұмыстарын жүргізуді және бұл мәселеде жан-жақты стандарттауды талап етеді. Қазіргі уақытта терминдер, анықтамалар, белгілеулер, тісті доңғалақтың элементтері мен іліністері, берілістің негізгі параметрлері, геометриясын есептеу, цилиндрлі эвольвентті берілістерді беріктікке есептеу, тістерді кесуге арналған құралдар және басқа да көпшіліктері стандартталған.
Кез-келген тісті берілістің негізгі кинематикалық сипаттамасы -
беріліс саны
. Стандарт бойынша ол
 дөңгелек тістерінің санының
дөңгелек тістерінің санының
 шестерня тістерінің санына қатынасымен анықталады және
шестерня тістерінің санына қатынасымен анықталады және
 деп белгіленеді, сонымен
деп белгіленеді, сонымен
 (1)
(1)
Берілістік қатынас басқада механикалық берілістердегі сияқты анықталады:
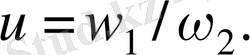 (2)
(2)
Тісті берілістердегі энергияның жоғалуы берілістің түріне, оны жасау дәлдігіне, майлауына байланысты және іліністердегі, білік тіректеріндегі үйкелістерге және (жабық берілістердегі) майды шашырату мен араластыруға кететін энергиялардан құралады. Жоғалатын механикалық энергия жылу энергиясына ауысып, кейбір жағдайларда тісті берілістерге жылулық есептеу жүргізу жүргізуге мәжбүрлік етеді.
Іліністердегі энергияның жоғалуы
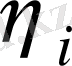 коэффициентімен, бір жұп подшипниктегі -
коэффициентімен, бір жұп подшипниктегі -
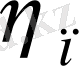 коэффициентімен, ал майды шашырату мен араластыруға кететін -
коэффициентімен, ал майды шашырату мен араластыруға кететін -
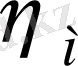 коэффициентімен сипатталады. Жабық бір сатылы берілістің жалпы ПӘК
коэффициентімен сипатталады. Жабық бір сатылы берілістің жалпы ПӘК
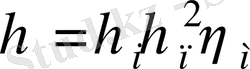 (3)
(3)
өрнегімен есептеледі.
Меже бойынша
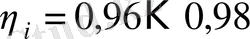 (жабық берілістер),
(жабық берілістер),
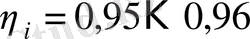 (ашық берілістер),
(ашық берілістер),
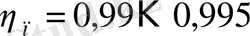 (домалау подшипниктерінде),
(домалау подшипниктерінде),
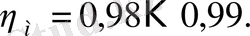
Берілген беріліс қатынасын қамтамасыз ететін доңғалақтардың өзара әсер ететін тістерінің беттерін жанасу беттері деп аталады. Тісті доңғалақтардан құралған кинематикалық жұптағы қозғалыстың берілу процессін тісті ілініс деп атайды.
- Тісті берілістер теориясының негіздері
Екі дененің тұрақты беріліс қатынасымен үздіксіз ілінісін қамтамасыз ету үшін олардың жанасу беттері, негізгі ілінісу заңдылығын қанағаттандыратын, қисықтармен сызылуы тиіс. Ол заң былайша тұжырымдалады: жанасқан профильдердің түйісу нүктесінен, оларға түсірілген ортақ нормаль, өс аралық қашықтықты бұрыштық жылдамдықтарының кері пропорционал қатынасындай бөліктерге бөледі.
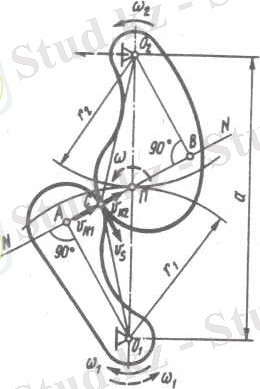 Келтірілген теорема тұжы-рымдамасын дәлелдеу үшін қозғалмайтын
Келтірілген теорема тұжы-рымдамасын дәлелдеу үшін қозғалмайтын
 және
және
 өстердің төңірегінде тұрақты
өстердің төңірегінде тұрақты
 және
және
 бұрыштық жылдамдық-тармен айналатын екі ілініскен денелерді қарастырайық (2 - сурет) .
бұрыштық жылдамдық-тармен айналатын екі ілініскен денелерді қарастырайық (2 - сурет) .
Бір дененің екіңші денеге күш қысымын беру үшін олардың түйісу
 нүктесінде, басқасына
нүктесінде, басқасына
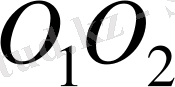 центрлік сызықты кесіп өтетін, жанасу профильдерінің ортақ нормалі
центрлік сызықты кесіп өтетін, жанасу профильдерінің ортақ нормалі
 болуы тиіс. Айналу центрлерінен
болуы тиіс. Айналу центрлерінен
 нормаліне
нормаліне
 және
және
 перпендикулярларын түсіреміз, ал
перпендикулярларын түсіреміз, ал
 нүктесінен радиустері
нүктесінен радиустері
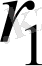 және
және
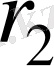 шеңберлердің екі доғасын жүргіземіз. Айналмалы қозғалыстың заңдылығына сәйкес, екі дененің түйісу
шеңберлердің екі доғасын жүргіземіз. Айналмалы қозғалыстың заңдылығына сәйкес, екі дененің түйісу
 нүктесінің жылдамдық векторлары, айналу центрлерінен түйісу нүктесіне жүргізілген радиустерге перпендикуляр және олардың модульдері
нүктесінің жылдамдық векторлары, айналу центрлерінен түйісу нүктесіне жүргізілген радиустерге перпендикуляр және олардың модульдері
және
.
Ойша екі дененің түйісу
 нүктесінің жылдамдық векторларын профильдің нормалі мен жанамасының бағыттарына жіктейміз; стандарт бойынша, нормальдық құраушыларын
нүктесінің жылдамдық векторларын профильдің нормалі мен жанамасының бағыттарына жіктейміз; стандарт бойынша, нормальдық құраушыларын
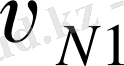 және
және
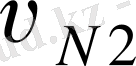 деп белгілеп
нормаль түйісу жылдамдығы
деп атаймыз, ал жанама құрамасын
деп белгілеп
нормаль түйісу жылдамдығы
деп атаймыз, ал жанама құрамасын
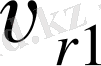 және
және
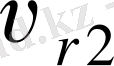 деп белгілеп
жанама түйісу жылдамдығы
деп атаймыз (олар 2 - суретте көрсетілмеген) .
деп белгілеп
жанама түйісу жылдамдығы
деп атаймыз (олар 2 - суретте көрсетілмеген) .
Әрейне, екі дененің үздіксіз іліністе болулары үшін
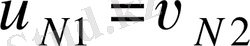
болулары тиіс, өйткені кері жағдайда бірінші дене екіншісіне еніп кетуі керек немесе одан қалып қоюы керек. Тағыда айқын жәйт,
 және
және
 тнүктелерінің абсолюттік жылдамдықтары
тнүктелерінің абсолюттік жылдамдықтары
 нормалі бойымен бағытталған және бұл жылдамдықтар нормаль түйісу жылдамдықтарымен тең болулары керек, яғни
нормалі бойымен бағытталған және бұл жылдамдықтар нормаль түйісу жылдамдықтарымен тең болулары керек, яғни
кері жағдайда түйісуші денелердің өлшемдерінде өзгерістер болар еді.
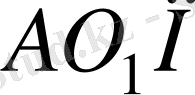 және
және
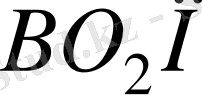 үшбұрыштарының ұқсастығын және
үшбұрыштарының ұқсастығын және
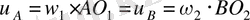 екендіктерін еске ала отырып,
екендіктерін еске ала отырып,

теңдігін аламыз, олай болса
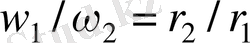 немесе
немесе
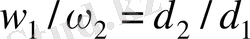 .
.
Сонымен,
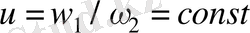 тұрақты беріліс қатынасын сақтау үшін,
ілініс полюсі
деп аталатын,
тұрақты беріліс қатынасын сақтау үшін,
ілініс полюсі
деп аталатын,
 нүктесі центрлер сызығында тұрақты орынды сақтауы және өсаралық
нүктесі центрлер сызығында тұрақты орынды сақтауы және өсаралық
 қашықтығын
қашықтығын
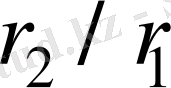 қатынасында бөлуге тиіс. Теорема дәлелденді.
қатынасында бөлуге тиіс. Теорема дәлелденді.
Негізгі ілініс заңдылығының жалпылама сипаттмалық мәні бар және ол беріліс қатынасы уақыт өте өзгеретін, яғни
 жағдайға да қолдануға болады. Бұл жәйтте ілініс полюсі тұрақты болып қалмайды, центрлер сызығы бойымен қозғалатын болады, ал осы сияқты қозғалыс жасайтын механизмдердің тісті доңғалақтары дөңгелек болмайды.
жағдайға да қолдануға болады. Бұл жәйтте ілініс полюсі тұрақты болып қалмайды, центрлер сызығы бойымен қозғалатын болады, ал осы сияқты қозғалыс жасайтын механизмдердің тісті доңғалақтары дөңгелек болмайды.
Радиустары
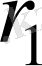 және
және
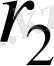 полюстен өтетін шеңберлерді
бастапқы
немесе
алғашқы шеңберлер
деп аталады. Осы шеңберлерде жататын нүктелердің шеңберлік жылдамдақтары бірдей болады
полюстен өтетін шеңберлерді
бастапқы
немесе
алғашқы шеңберлер
деп аталады. Осы шеңберлерде жататын нүктелердің шеңберлік жылдамдақтары бірдей болады
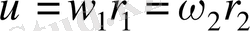 . (4)
. (4)
Дененің салыстырмалы қозғалысын қарастыру үшін механизмдер мен ашиналар теориясында пайдаланатын
қозғалысты ұстау әдісін
(қозғалысты тоқтату әдісін) қолданайық, яғни барлық жүйеге
 нүктесінің төңірегінде
нүктесінің төңірегінде
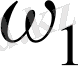 бұрыштық жылдамдықпен, алғашқы бағытына қарама-қарсы, айналуына жағдай жасалық (3,
а
- сурет) . Онда бірінші дене тоқтайды, екіншісі
бұрыштық жылдамдықпен, алғашқы бағытына қарама-қарсы, айналуына жағдай жасалық (3,
а
- сурет) . Онда бірінші дене тоқтайды, екіншісі
 және
және
 өстерінің төңірегінде бірмезгілде айналатын, күрделі жазық параллель қозғалыс жасайды, ал оның бірінші қозғалмайтын денеге қарағандағы қозғалысын, теориялық механикадан белгілі жылдамдықтың лездік центрі әдісін пайдаланып, қарастыруымызға болады.
өстерінің төңірегінде бірмезгілде айналатын, күрделі жазық параллель қозғалыс жасайды, ал оның бірінші қозғалмайтын денеге қарағандағы қозғалысын, теориялық механикадан белгілі жылдамдықтың лездік центрі әдісін пайдаланып, қарастыруымызға болады.
Жоғарыда радиустары
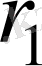 және
және
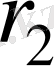 алғашқы шеңберлерде жататын нүктелердің шеңберлік жылдамдақтары бірдей болатындығын атап өткенбіз, олай болса, егер бірінші шеңбер тоқтатылған болса, онда екіншісі біріншісінің үстімен тайғанаусыз айналады, ал
алғашқы шеңберлерде жататын нүктелердің шеңберлік жылдамдақтары бірдей болатындығын атап өткенбіз, олай болса, егер бірінші шеңбер тоқтатылған болса, онда екіншісі біріншісінің үстімен тайғанаусыз айналады, ал
 нүктесі екінші дененің жылдамдығының лездік центірі болады.
нүктесі екінші дененің жылдамдығының лездік центірі болады.
 лездік бұрыштық жылдамдықты анықтау үшін
лездік бұрыштық жылдамдықты анықтау үшін
 өстінің жылдамдығын келесі теңдеу түрінде жазайық
өстінің жылдамдығын келесі теңдеу түрінде жазайық
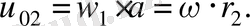
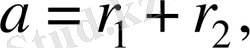 ал
ал
 болғандықтан,
болғандықтан,
Сонымен, бірінші денені тоқтатқаннан кейін екінші дене полюстің төңірегінде
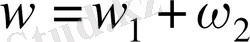 лездік бұрыштық жылдамдықпен айналады. Мұнан екінші дененің түйісу
лездік бұрыштық жылдамдықпен айналады. Мұнан екінші дененің түйісу
 нүктесі бірінші дененің бетімен
нүктесі бірінші дененің бетімен
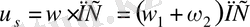 (5)
(5)
немесе
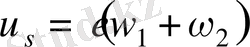 (6)
(6)
жылдамдығымен тайғанайтынын байқаймыз
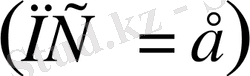 . Бұл жылдамдықты
түйісу нүктелерінің тайғанау жылдамдығы
деп атайды. Тайғау жылдамдығы түйісу нүктелерінің полюстен қашықтығына тура пропорционал. Түйісу нүктелерінің тайғанауы
үйкеліспен
қабаттас болады (3,
b
- сурет) .
. Бұл жылдамдықты
түйісу нүктелерінің тайғанау жылдамдығы
деп атайды. Тайғау жылдамдығы түйісу нүктелерінің полюстен қашықтығына тура пропорционал. Түйісу нүктелерінің тайғанауы
үйкеліспен
қабаттас болады (3,
b
- сурет) .
Денелер полюсте ілініскенде тайғанау жылдамдығы нөлге тең болады, ал түйісу нүктесі полюстен өткеннен кейін тайғанау жылдамдығының векторы, үйкеліс күші сияқты, бағытын қарама-қарсыға өзгертетіні анық, яғни тайғанау жылдамдығы полюсте нөлге тең, ал полюстен өткен кезде таңбасын өзгертеді .
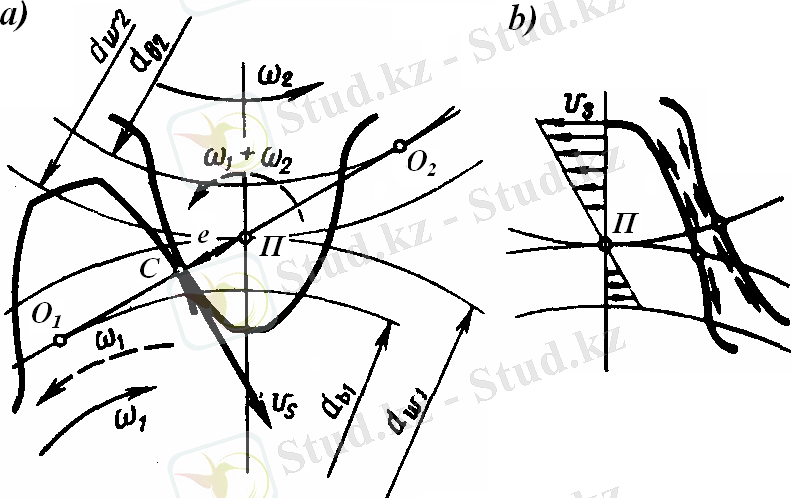 Ең үлкен тай-ғанау тістердің ба-сында және аяғында болады (3,
b
- сурет), бастапқы шеңберде нөлге тең және таңбасын өзгер-теді. Тайғанау үйке-ліспен болады. Үйке-ліс іліністегі шығын-ның және тістердің тозуының себебі болып табылады
.
Жетекші тістерде үйкеліс күштері бастапқы шеңбермен бағытталса, жетектегі тістерде керісінше бағытталады. Доңғалақтың диаметрі тұрақты болғанда, тістің биіктігі мен іліністің модулін өсіргенде,
Ең үлкен тай-ғанау тістердің ба-сында және аяғында болады (3,
b
- сурет), бастапқы шеңберде нөлге тең және таңбасын өзгер-теді. Тайғанау үйке-ліспен болады. Үйке-ліс іліністегі шығын-ның және тістердің тозуының себебі болып табылады
.
Жетекші тістерде үйкеліс күштері бастапқы шеңбермен бағытталса, жетектегі тістерде керісінше бағытталады. Доңғалақтың диаметрі тұрақты болғанда, тістің биіктігі мен іліністің модулін өсіргенде,
 қашықтығы өседі, демек, сырғанау өседі. Ірі модульді, тістері аз доңғалақтарға қарағанда уақ модульді, көп тісті доңғалақтарда тайғанау аз, ал ПӘК-і жоғары болады.
қашықтығы өседі, демек, сырғанау өседі. Ірі модульді, тістері аз доңғалақтарға қарағанда уақ модульді, көп тісті доңғалақтарда тайғанау аз, ал ПӘК-і жоғары болады.
Іліністің негізгі заңының талаптарын көптеген қисықтар қанағат ете алады, ал кеңінен пайдаланылатыны XVIII ғасырдың ортасында Л. Эйлер ұсынған эвольвентті ілініс. Сонымен қатар, машина жасауда 1954 ж. М. Л. Новиков ұсынған дөңгелек ілініс те, ал аспап жасауда - циклоидты және тағыда басқа іліністер де қолданылады.
- Эвольвентті іліністің қасиеттері
Эвольвента
немесе
шеңбердің жазбасы
деп, қозғалмайтын шеңбердің бетімен тайғанаусыз сырғанайтын
 түзуінің кезкелген нүктесінің сызатын жазық қисығын айтады (4 - сурет) .
түзуінің кезкелген нүктесінің сызатын жазық қисығын айтады (4 - сурет) .
 түзуін
туындататын түзу
деп, ал осы түзудің сырғанайтын диаметрі
түзуін
туындататын түзу
деп, ал осы түзудің сырғанайтын диаметрі
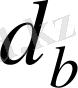 шеңберін
негізгі шеңбер
деп атайды. Туындататын түзудің негізгі шеңбердің бетімен тайғанаусыз сырға-найтыны олардың әрбір мезетте түйісетін нүктелері жылдамдықтың лездік центрі және эвольвентаның қиссықтық центрі болып табылатынын көрсетеді. Сондықтан, туындататын түзу өзінің әрбір жағдайын-да эвольвентаның нормалі болады, басқаша айтқанда, эвольвентаның нормалі әрқашан негізгі жеңбердің жанамасы болып табылады.
шеңберін
негізгі шеңбер
деп атайды. Туындататын түзудің негізгі шеңбердің бетімен тайғанаусыз сырға-найтыны олардың әрбір мезетте түйісетін нүктелері жылдамдықтың лездік центрі және эвольвентаның қиссықтық центрі болып табылатынын көрсетеді. Сондықтан, туындататын түзу өзінің әрбір жағдайын-да эвольвентаның нормалі болады, басқаша айтқанда, эвольвентаның нормалі әрқашан негізгі жеңбердің жанамасы болып табылады.
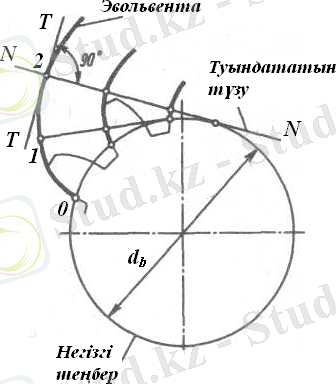 Эвольвентаның құрылу тәсілінен, бұл қисықтың шеңбердің ішінде болуы мүмкін еместігі шығады. Егер туындататын түзуді қарама қарсы бағытта сырғанайтын болса, онда эвольвентаның басқа - солжақ тармағын аламыз. Әрбір эвольвентті іліністі доңғалақтың тістері эвольвенттің оң және сол бөліктерімен сызылады. Тістің негізгі шеңбер ішіндегі формасы тіс кесетін құралдың профилімен анықталады. Екі бір текті (оң және сол жақтағы) эвольвенттер
эквидистантты
(тең арақашықты)
қисықтар
, яғни эвольвенттердің бастапқы нүктелерінің арасы негізгі шеңбердің доғасына тең аралықпен, кезкелген жалпы нормальда өзара бірдей қашықтықта жатады.
Эвольвентаның құрылу тәсілінен, бұл қисықтың шеңбердің ішінде болуы мүмкін еместігі шығады. Егер туындататын түзуді қарама қарсы бағытта сырғанайтын болса, онда эвольвентаның басқа - солжақ тармағын аламыз. Әрбір эвольвентті іліністі доңғалақтың тістері эвольвенттің оң және сол бөліктерімен сызылады. Тістің негізгі шеңбер ішіндегі формасы тіс кесетін құралдың профилімен анықталады. Екі бір текті (оң және сол жақтағы) эвольвенттер
эквидистантты
(тең арақашықты)
қисықтар
, яғни эвольвенттердің бастапқы нүктелерінің арасы негізгі шеңбердің доғасына тең аралықпен, кезкелген жалпы нормальда өзара бірдей қашықтықта жатады.
Негізгі шеңбердің
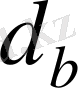 диаметрін үлкейткен сайын эвольвентаның қисықтық радиусы өсе бастайды, ал шектік
диаметрін үлкейткен сайын эвольвентаның қисықтық радиусы өсе бастайды, ал шектік
 жағдайында эвольвента түзуге айналатына айқын. Демек, эвольвентті іліністі рейканың тістерінің профилі түзу сызықты болулары тиіс. Сондықтан да эвольвентті іліністі цилиндірлі және конусты тісті доңғалақтарды жобалау негізіне тістері түзу сызықты профильді рейканың контуры болып табылатын (4 - сурет),
стандартты алғашқы контурлар
қабылданған.
жағдайында эвольвента түзуге айналатына айқын. Демек, эвольвентті іліністі рейканың тістерінің профилі түзу сызықты болулары тиіс. Сондықтан да эвольвентті іліністі цилиндірлі және конусты тісті доңғалақтарды жобалау негізіне тістері түзу сызықты профильді рейканың контуры болып табылатын (4 - сурет),
стандартты алғашқы контурлар
қабылданған.
 және
және
 өстерінің төңірегінде
өстерінің төңірегінде
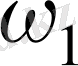 және
және
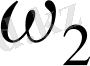 бұрыштық жылдамдықпен айналатын доңғалақтардың екі тісінің эвольвентті ілініс сызбасын (5 - сурет) қарастырайық.
бұрыштық жылдамдықпен айналатын доңғалақтардың екі тісінің эвольвентті ілініс сызбасын (5 - сурет) қарастырайық.
Тісті доңғалақтар жұбының кішісін
шестерня
деп, ал үлкенін
доңғалақ
деп атайды. «Тісті доңғалақ» деген термин ортақ болып табылады. Шестерняның параметрлеріне
1
, ал доңғалақтың параметрлеріне
2
индексін қосымша жазады (5 - сурет) . Мұнымен қатар тісті берілісте мынадай индикстер де пайдаланылады: алғашқы бетке немесе шеңберге қатысты
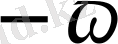 ; негізгі бетке немесе шеңберге қатысты
; негізгі бетке немесе шеңберге қатысты
 ; тістердің бастары мен төбелерінің беттеріне немесе шеңберлеріне қатысты
; тістердің бастары мен төбелерінің беттеріне немесе шеңберлеріне қатысты
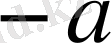 ; тістердің табандары мен ойыстарының беттеріне немесе шеңберлеріне қатысты
; тістердің табандары мен ойыстарының беттеріне немесе шеңберлеріне қатысты
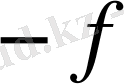 . Бөлгіш бетке немесе шеңберге қатысты параметрлерге қосымша индикс қолданылмайды.
. Бөлгіш бетке немесе шеңберге қатысты параметрлерге қосымша индикс қолданылмайды.
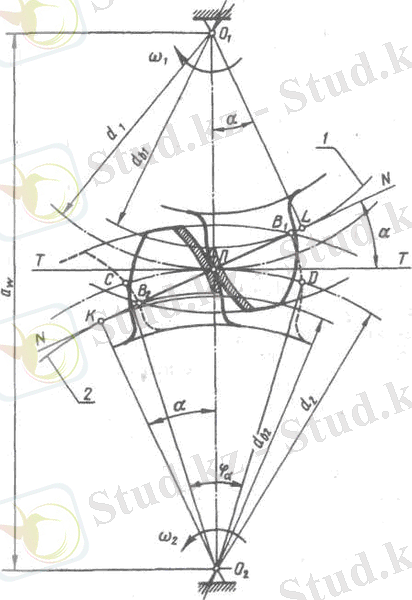 Тісті доңғалақтар жұбының параметрлері жөніндегі негізгі ұғым-дарды және олардың өзара байланыстарын түзу тісті доңғалақтерды қарастырып ұғыну жеңілдеу болады. Бұл жағдайда қиғаш доңға-лақтардың ерекшіліктері қосымша қарастырыла-ды.
Тісті доңғалақтар жұбының параметрлері жөніндегі негізгі ұғым-дарды және олардың өзара байланыстарын түзу тісті доңғалақтерды қарастырып ұғыну жеңілдеу болады. Бұл жағдайда қиғаш доңға-лақтардың ерекшіліктері қосымша қарастырыла-ды.
 және
және
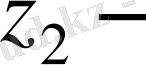 шестерня және доңғалақ тістерінің саны;
шестерня және доңғалақ тістерінің саны;
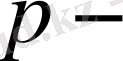 тістердің бөлгіш шеңбер-лік адымы (алғашқы тісті рейканың адымына тең) ;
тістердің бөлгіш шеңбер-лік адымы (алғашқы тісті рейканың адымына тең) ;
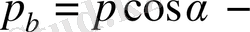 тістердің негізгі шеңберлік адымы;
тістердің негізгі шеңберлік адымы;
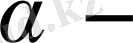 профильдің бөлгіш бұрышы (берілген контур профилінің бұрышына тең), 13755-81 МЕСТ бойынша
профильдің бөлгіш бұрышы (берілген контур профилінің бұрышына тең), 13755-81 МЕСТ бойынша
 ;
;
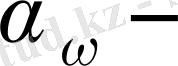 ілінісу бұрышы немесе профильдің бастапқы бұрышы,
ілінісу бұрышы немесе профильдің бастапқы бұрышы,
; (7)
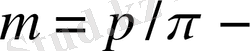 тістердің шенберлік бөлгіш модулі (
тістердің модулі
- тіс өлшемдерінің негізгі сипаттамасы) . Іліністегі доңғалақ жұптарының модульдері бірдей болуы тиіс. Цилиндрлік және конусты берілістердің тістер модулі МЕСТ-пен реттелген 1-ден 14 мм дейінгі стандартталған модульдердің мәндері 1. 1 - кестеде келтірілген;
тістердің шенберлік бөлгіш модулі (
тістердің модулі
- тіс өлшемдерінің негізгі сипаттамасы) . Іліністегі доңғалақ жұптарының модульдері бірдей болуы тиіс. Цилиндрлік және конусты берілістердің тістер модулі МЕСТ-пен реттелген 1-ден 14 мм дейінгі стандартталған модульдердің мәндері 1. 1 - кестеде келтірілген;
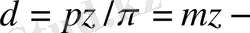 бөлгіш диаметрі (кескіш құрал кесу кезінде жылжитын шеңбердің диаметрі) ;
бөлгіш диаметрі (кескіш құрал кесу кезінде жылжитын шеңбердің диаметрі) ;
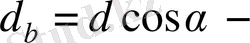 негізгі диаметр (жаймасы тістердің эвольвентасы болатын шеңбердің диаметрі) ;
негізгі диаметр (жаймасы тістердің эвольвентасы болатын шеңбердің диаметрі) ;
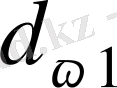 және
және
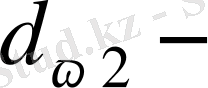 бастапқы диаметрлер (тісті доңғалақтар жұбының бірімен-бірі сырғанаусыз жанасып айналатын шеңберлердің диаметрлері, бұларды бастапқы беттер немесе шеңберлер деп атайды) :
бастапқы диаметрлер (тісті доңғалақтар жұбының бірімен-бірі сырғанаусыз жанасып айналатын шеңберлердің диаметрлері, бұларды бастапқы беттер немесе шеңберлер деп атайды) :
;
. (8)
1. 1 - кесте
Бастапқы және бөлгіш шеңберлердің диаметрлері, ығыспайтын берілістерде және қосынды ығысу шамасы (төменнен қара)
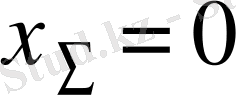 болғанда, сәйкес болады:
болғанда, сәйкес болады:
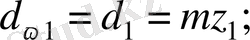
(9)
Доңғалақтарды жылжытып кескенде (төменнен қара) :
- өсаралық қашықтық;
,
мұндағы
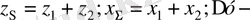
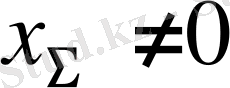 болған кездегі теңдестіріп жылжыту коэффициенті. Түзетілмеген берілістер үшін және
болған кездегі теңдестіріп жылжыту коэффициенті. Түзетілмеген берілістер үшін және
 немесе
немесе
 ,
,
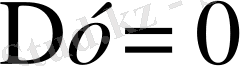 болған кезде
болған кезде
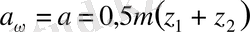 ,
,
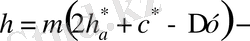 тістің биіктігі;
тістің биіктігі;
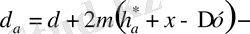 тіс дөңестер шеңберінің диаметрі;
тіс дөңестер шеңберінің диаметрі;
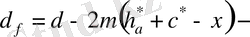 тіс ойығы шеңберінің диаметрі;
тіс ойығы шеңберінің диаметрі;
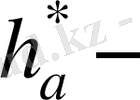 тістің басының биіктік коэффициенті (13755-81 МЕСТ бойынша
тістің басының биіктік коэффициенті (13755-81 МЕСТ бойынша
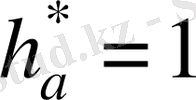 ) ;
) ;
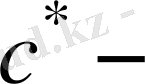 радиалдық саңылау коэффициенті (13755-81 МЕСТ бойынша
радиалдық саңылау коэффициенті (13755-81 МЕСТ бойынша
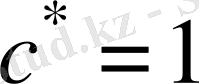 ) .
) .
Түзетілмеген дөңгелектер үшін
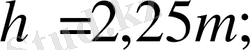
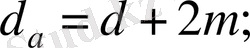
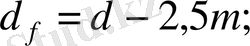
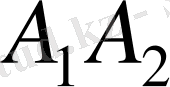 - ілінісу сызығы;
- ілінісу сызығы;
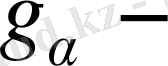 активті ілінісу сызығының ұзындығы;
активті ілінісу сызығының ұзындығы;
 - ілінісу полюсі.
- ілінісу полюсі.
- Үстемелеу коэффициенті және тістің профилі бойымен күштің өзгеруі
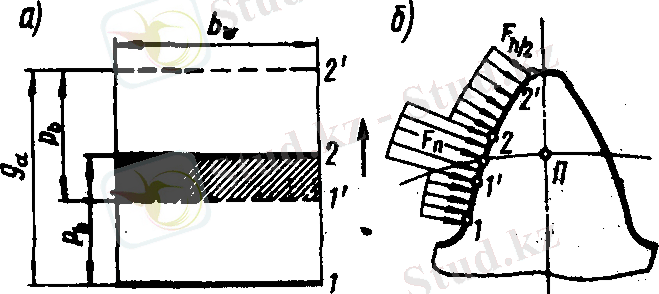
Дөңгелектер айналғанда (5-сурет) тістердің жанасу сызығы ілініс аймағында (в поле) орын ауыстырады (6, а-сурет) .
6 - сурет
Бірінші жұп тістердің жанасу сызығы
1
ілініс аймағының басында тұрғанда,
 болған кезде, ілініс аймағында екінші жұп тістердің жанасу сызығы
2
тұрады. Дөңгелектер айналған кезде
1
және
2
сызықтар стрелкамен көрсетілген бағытта орын ауыстырады. Екінші жұп аймақ шетіне келгенде
2
/
, бірінші жұп
1
/
орынға келеді. Одан әрі қозғалған кезде
1
/
…
2
аралығында тістердің тек бір жұбы ілініседі.
1
жұбы
2
-орынға келгенге дейін біржұпты ілініс жалғаса береді. Осы кезде ілініске тістердің келесі жұбы түседі де, екіжұпты ілініс жаңадан басталады.
болған кезде, ілініс аймағында екінші жұп тістердің жанасу сызығы
2
тұрады. Дөңгелектер айналған кезде
1
және
2
сызықтар стрелкамен көрсетілген бағытта орын ауыстырады. Екінші жұп аймақ шетіне келгенде
2
/
, бірінші жұп
1
/
орынға келеді. Одан әрі қозғалған кезде
1
/
…
2
аралығында тістердің тек бір жұбы ілініседі.
1
жұбы
2
-орынға келгенге дейін біржұпты ілініс жалғаса береді. Осы кезде ілініске тістердің келесі жұбы түседі де, екіжұпты ілініс жаңадан басталады.
Ілініс аймағынан тістің профиліне келсек (6, б - сурет), мыналарды байқаймыз: біржұпты ілініс
1
/
…2
аймағы тістің ортасында орналасады. Біржұпты ілініс аймағында тіс толық
 күшін, ал екіжұпты ілініс аймағында (шамамен) тек күштің жартысын береді. Біржұпты ілініс аймағының өлшемі үстемелеу коэффициентінің шамасына байланысты:
күшін, ал екіжұпты ілініс аймағында (шамамен) тек күштің жартысын береді. Біржұпты ілініс аймағының өлшемі үстемелеу коэффициентінің шамасына байланысты:
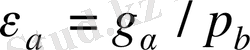 . Іліністің үздіксіздігі және жүрістің ырғақтылығы шарты бойынша
. Іліністің үздіксіздігі және жүрістің ырғақтылығы шарты бойынша
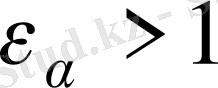 болуы керек (есептелуі төменде келтіріледі) .
болуы керек (есептелуі төменде келтіріледі) .
- Тісті берілістің дәлдігі.
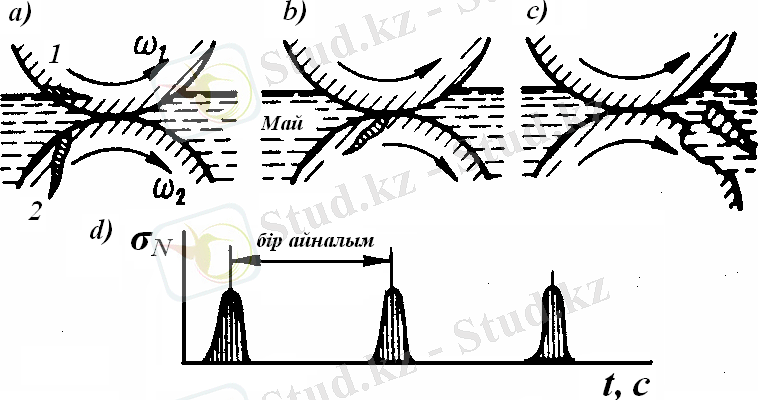
Тісті берілістер белгілі бір дәлдікке сәйкес жасалуы керек. Ал ондай дәлдік төмендегі көрсеткіштермен анықталады:
- Кинематикалық дәлдік, яғни өзара ілініскен тісті дөңгелектердің бір айналым жасаған кездегі бұрылу бұрыштарының айырмашылығын көрсетеді.
- Берілістің бірқалыптылығы: дөңгелектің бір айналғандағы жылдамдығының өзгеруімен сипатталады. Егер беріліс бірқалыпты болмаса, онда ол зиянды дыбыстың пайда болуына, айнымалы күштердің және тербелістердің көбеюіне әкеп соғады. Бұл шапшаң айналатын берілістердің жұмыс істеу қабілетін азайтады. Осыдан барып беріліс бөлшектері тез істен шығады. Берілістің бірқалыптылығы арнаулы құралдармен өлшенеді.
- Тістің бүйір бетіндегі дақ арқылы анықталатын дәлдік. Бұл дәлдікті анықтау үшін тістің бүйір бетін майлайды (бояйды) . Содан кейін өзара ілініскен тісті дөңгелектерді айналдырады. Дөңгелектерді айналдырғанда, олардың тістерінің бүйірінде май дақтары пайда болады. Осы дақтардың орналасуына байланысты тісті берілістердің дәлдігін анықтайды. Бұл дәлдік көбінесе жинап, құрастыру кезіндегі қателіктерді көрсетеді.
4. Тістің еркін айналуына жағдай жасау үшін, оның жұмыс істемейтін бүйірінде аздаған саңылау қалдырады. Бұл тістер қызған кезде, олардың қысылып, бір -біріне жабысып қалмауы үшін жасалады.
Тісті дөңгелектерді дайындағанда 6, 7, 8 дәлдік дәрежелері көп қолданылады. Ілінісу кезінде тістердің жұмыс істемейтін бетіндегі саңылаулар стандартталған, МЕСТ 1643-81 бойынша олар саңылау өлшемі өсуіне байланысты төмендегіше орналасқан: Н- нөлдік саңылау; Е- кіші саңылау; С және Д-кішірейтілген саңылау; В-қалыпты саңылау; А-үлкен саңылау. Сондай-ақ, көрсетілген стандарт өсаралық қашықтығының ауытқуын да шектейді. Н, Е және Д саңылаулары дәл дайындауды қажет етеді және екі жаққа бірдей айналатын берілістерде қолданылады. Тісті берілістерде тістердің жұмыс істемейтін беттерінде қалыпты саңылау (В) кеңінен қолданылады. Тісті дөңгелек дәлдік дәрежесі және жұмыс істемейтін бүйірінің саңылауы белгінеді. Мысалы, 6-В МЕСТ 1643-81. Бұл 6-дәрежелі дәлдікті және қалыпты бүйір саңылаулы берілісті көрсетеді.
- Жанасу кернеулері және жанасу беріктігі.
Мәшиненің екі бөлшегі бірімен-бірі бетпе-бет жанасып жатса және жанасу ауданы өте аз болса (нүктелі - екі шардың қысылуы, шар мен жазықтықтың жанасуы немесе сызықтық - екі цилиндрдің жанасуы), сол жанасу бетінде едәуір күш кернеуі пайда болады (7 - сурет) .
Бұл кернеуді
жанасу кернеуі
деп атайды және
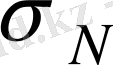 деп белгілейді. Егер жанасу кернеулерінің мәні мүмкіндік жанасу кер-неулерінің мәнінен үлкен болса, бөлшектер бетінде шетінеулер пайда болады. Мысалы. тісті, червякті және т. б. берілістерде, подшип-никтерде осындай бұзылулар байқалады.
деп белгілейді. Егер жанасу кернеулерінің мәні мүмкіндік жанасу кер-неулерінің мәнінен үлкен болса, бөлшектер бетінде шетінеулер пайда болады. Мысалы. тісті, червякті және т. б. берілістерде, подшип-никтерде осындай бұзылулар байқалады.
Жанасу кернеуінің шамасы
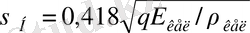 , (10)
, (10)
мұндағы
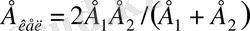 , (11)
, (11)
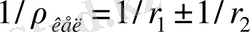 , (12)
, (12)
мұндағы
 және
және
 - келтірілген серпімділік модулі және келтірілген жанасу қисығының радиусы;
- келтірілген серпімділік модулі және келтірілген жанасу қисығының радиусы;
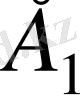 ,
,
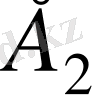 ,
,
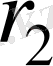 - серпімділік модульдері және жанасу қисықтарының радиустары. (11) -формуладағы «-» таңбасы іштей жанасқанда қолданылады.
- серпімділік модульдері және жанасу қисықтарының радиустары. (11) -формуладағы «-» таңбасы іштей жанасқанда қолданылады.
Тістер әлсіреген кезде олардың сыртқы қабаты үгіледі. Бұл жағдайда ең алдымен тістің бетінде өте кішкентай жарықша пайда болады, одан кейін ол жерге май кіріп, оның үлкеюіне себепші болады (8 - сурет) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz