Бастауыш сынып математикасында оқушылардың білім деңгейін арттыруда ойындық пәндік орта мен мұғалімнің іс-әрекеті


КІРІСПЕ
I. Ойын түрлері
II. Алгебралық өрнек
III. Бастауыш сыныпта математика сабақтарында оқушылардың білім деңгейін арттырудағы мұғалімні іс-әрекеті
ҚОЫТЫНДЫ
ӘДЕБИЕТТЕР ТІЗІМІ
КІРІСПЕ
Қоғамдағы саяси-экономикалық, мәдени өзгерістерге байланысты оқыту жүйесіне де өзгертулер енгізілді. Қоғам өмірі ең алдымен адамның (баланың) өздігінен дамуы мен жетілуін іске асыратын, педагогикалық теория мен практикаға ерекше мән бере бастады.
Оқушының дербестігін, шығармашылық ынтасын арттыруға бағытталған педагогикалық жүйе қазіргі білім берудің барабар талабы болып табылады.
Жеке бала - бұл күрделі бүтін жүйе және оның дамуын ашатын жүйеқұрағыш бөлігін табу өте маңызды. Сол бөлік ретінде ғалымдар өздігінен танымдылықты бөледі, ол жеке адамның дамуындағы бүтін интегралдық көрсеткіші, адамға жаңа жағдайда жеңіл жөн табуға, өзге жағдайда білім мен дағдысын қолдануға мүмкіндік береді. Сондықтан адамның өзіндік танымдылығын дамыту маңызды және мәнді мәселе.
Жеке баланың өздігінен танымдылығын дамыту үшін көптеген факторлар әсер етеді: стихиялық (апаттық) және арнайы ұйымшылдық, табиғи және әлеуметтік факторлар. Басқа факторлармен қатар ғалымдар мен педагог-практиканттар қоршаған ортаның әсерін көрсетеді. Ол ортада бала жеке адам ретінде дамиды, оған әсер етудің арқасында өзінің өздігін көрсетеді.
Ғалымдар білім ортасының құрылымдық бөлігі пәндік қоршауы деп көрсетеді. Пәндік қоршауды пәндік орта ретінде анықтап, қазіргі зерттеушілер оны іс-әрекеттің ұйымдасқан көзқарасында қарап (ұйымдасқан және ұйымдаспаған орта), оны белгілі бір ортада (ойын, оқу, еңбек) қарастырады.
Барлық теориялық және практикалық маңызды зерттеулерге қарамастан ойын - пән ортасында әлі де жеткіліксіз өңделмеген құру аспектілері кездеседі. «Ойын - пән ортасы» деген ұғымның мағынасы, оның құрылымы оқу - пән ортасында оқушылардың өзіндік танымдылығын дамытуды іске асыру механизмі.
I. Зерттеу жұмысының өзектілігі: келесі факторлармен көрсетуге болады:
- әлеуметке өздігінен танымды және өзін дамытуға жағдайы бар еркін адамның қажеттілігі;
- төменгі сынып оқушыларының өздігінен танымдылығын дамытуды зерттейтін, оның ғылыми негізін талдайтын оқу орындарының қажеттілігі;
- әр түрлі жастағы балалардың оқу - пән ортасында қолданылатын технологияларды зерттеу.
II. Зерттеудің мақсаты мен міндеттері :
Тәжірибелі зерттеудің барысында оқу - пән ортасының тиімділігін анықтау.
III. Зерттеудің әдісі:
Бала әрекетінің өнімін талдау, педагогикалық эксперимент, анкета, сұхбаттасу, бақылау; математикалық және статисталық материалдарды зерттеу әдістері.
IV. Зерттеудің жаңашылдығы мен практикалық маңыздылығы:
Ойын - пән ортасында субъекттің әрекетін ұйымдастыру технологиясы жоспарланды және қабылданды, ол келесі кезеңдермен беріледі: дайындық, репродуктивті іздеу, шығармашылық ізденіс, талдау. Пән қоршауы ретіндегі оқу - пән ортасы, ол баланы ойын әрекетіне әкеледі және оның жеке потенциалын дамытады.
V. Зерттеудің негізі:
- жеке әрекет жасауы жеке адамның өздігінен танылуына жағдай жасайды;
- жүйелі жағдай жасау, бұл педагогикалық құбылысты бір - бірімен байланысты және бір - бірімен келіскен бүтін жүйені құрастыратын диалектикалы жинақты қарастырады;
- әлеуметтік қатынастағы теорияны қарастырады.
I. Ойын түрлері
Математиканы оқытудың негізі болып ойын саналады. «Ойын» сөзі курс ұғымына кездейсоқ енген жоқ. Психологтардың дәлелдеулері бойынша 6-10 жастағы балалардың негізгі әрекеті ойын болып саналады.
дылық ДЫЛЫҚТЫ ДАМЫТУДЫҢ ҚАЗІРГІ ҚОҒАМНЫҢ КЕЛЕЛІ МӘСЕЛЕСІОқыту - күрделі және көпжақты процесс.
Әр ойынның басты мақсаты - материалды түсініп, бекітуге көмектесу.
Мысал ретінде 1, 2, 3-сыныптарда өтілетін ойындарды қарастырайық.
«Балық, құс, аң, . . . » ойыны
Сыныпта жүргізуші «балық, құс, аң . . . » деген сөздерді айтып өтеді. Кенет бір сөзде тоқтап оқушыны көрсетеді. Оқушы не балықты, не құсты, не аңды атайды (ол жүргізушінің қай сөзде тоқтағанына байланысты) . Ойынның мақсаты:
- балалар өздеріне таныс жануарларды атауға үйренеді;
- таныс емес жануарларды таниды;
- сыныптастарын зейін қойып тыңдауға үйренеді;
- дұрыс жауапты тез тануға үйренеді;
- сыныптастардың жауабын дұрыс бағалауға үйренеді.
Бұл ойынды өзгертуге де болады. «Гүлдер, ағаштар, көкөністер, жемістер . . . » және тағы басқа.
«Қатарды жалғастыр» ойыны
Жүргізуші оқушыларға бір топтағы заттардың қатарын атайды (4-5түрін) .
Балалар бұл заттардың жалпы атауларын атап, қатарды жалғастырулары қажет. Мысалы, жүргізуші мынадай қатарды ұсынады: қаз, үйрек, торғай, қарға, . . немесе Астана, Москва, Лондон, . . .
«Күн-түн» ойыны
Балалар көзін жұмып, шынтақтарын үстел үстіне қояды. Жүргізуші он саны аясындағы сандарды алу және қосуға байланысты есептер айтады. Балалар көздерін ашпай саусақтарымен жауаптарын көрсету керек. Жүргізуші сыныпта жүріп балалардың қолдарын түртіп, жауаптың дұрыс не бұрыстығын айтады.
Ойынның мақсаты - балалардың көру аппаратын қоспай, есепті ауызша шығара білуге үйрету. Тәжірибе көрсеткендей, кейбір үлкен адамдар да саусақпен жауапты көрсетуге қиналады.
Алгебралық өрнекAlgebraic expression Саны шекті әріптермен сандардан құралған және бір-бірімен қосу, азайту, көбейту, бөлу бүтін санға дәрежелеу сондай ақ түбір табу амалдарының таңбалары арқылы біріктірілген өрнек. Еген өрнекке енетін әріптер түбір астында болмаса, онда алгебралық өрнек сол әріптерге қарағанда рационал алгебралық өрнек деп аталады. (мысалға өрнегі ға қарағанда рационал алгебралық өрнек) . Егер белгілі бір әріптер енетін өрнекте бөлу амалы болмаса, онда алгебралық өрнек сол әріптерге қарағанда бүтін алгебралық өрнек деп аталады. Егер кейбір әріптерді(не бәрін) айнымалы деп санасақ онда алгебралық өрнек алгебралық функцияға болады.
Анықталмаған теңдеуСандар теориясының аса маңызға ие, бай тарихы бар, мазмұны мол саласының бірі. Анықталмаған теңдеу деп белгісіздің саны теңдеудің санынан көп болатын теңдеулер жүйесін не теңдеуді айтамыз. Көне Гректің атақты математигі Диофант сонау Ⅲ ғысырдың басында-ақ осындай түрдегі теңдеулерді зеріттей бастаған, сондықтан кейде анықталмаған теңдеу Диофант теңдеуі деп те аталады. 1969 жылғы, Л. Ж. Модердің «Диофант теңдеуі » атты кітабы осы саладағы зеріттеулердің нәтижесін бір ретке келтіріп берді. Соңғы он жылда осы салада аса зор дамушылық байқалады. Дегенменен, жалпы жағдайға алып қарағанда, екінші дәрежеден жоғары анықталмаған теңдеулер туралы адамдардің білері шамалы. Енді бір жағынан, анықталмаған теңдеумен математиканың басқа салалары, мысалға, алгебралық сандар теориясы, алгебралық геометрия, терулер математикасы қатарлылармен тығыз байланысы бар, шекті топтар мен көркем модудауға да осы анықталмаған теңдеулерді қолдануға болады, осы себептен де математиканың осы бір көне саласы әлі де көптеген математиктердің назарын өзіне аударуда.
Архимед акциомасыArchimedes's axiom Ұзіндіқтарі әр тұрлі екі кесіндінің ұзінірағі мейлі қанша ұзын, қысқасы мейлі қанша қысқа болсада, ұзінірақ кесіндінің бойынан қысқарақ кесіндіге тең кесіндіні ұздіксіз қыйып алыуға болады, әрі мәлім рет кесіп алғаннан кейін мынадай жағдайдың : а-сурет не асып қалмайды, не қысқарақ кесіндіден де қысқа кесінді қалады. AB кесіндісі ұзінірақ кесінді, CD кесіндісі қысқарақ кесінді болсын, AB нің бойынан CD нің ұзіндіғіна тең болатын кесінділер қыйып алсақ, онда не AB=n CD (а -сурет), не nCD<AB<(n+1) CD ( b-сурет) келіп шығады.
Аполлониус теоремасы-1Үшбұрыштің қабырғалары мен орта сызықтары арасында мынадай тәулдіктер болады : △ABC нің үш қабырғасы жеке -жеке a, b, c, үш қабырғасының орта сызығы жеке -жеке ma, mb, mc десек онда
:
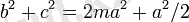
бұл теорема әдетте Аполлониус теоремасы деп аталады.
Аполлониус теоремасы-2Екі тұрақты нүктеден қашықтықтарының қатынасы бір тұрақты сан (1 ге тең емес сан) болатын нүктенің геометриялық орны шеңбер болады. Мысалы суреттегідей A, B екі тұрақті нүкте, P қозғалмалы нүкте, әрі M нүктесі AB-нің ішінде жатады, әрі, N нүктесі AB-нің сыртында жатады әрі, десек онда P нүктесінің геометриялық орны MN диаметрі болатын шеңбер болады. Бұл теорема Аполлониус теоремасы деп аталады, ал осы шеңбер Аполлониус шеңбері деп аталады.
Алгебралық функцияAlgebraic function қысқартылмайтын теңдеу
(1)
арқылы анықталған көп мәнді функция, мұндағы - z-тің көпмүшелігі. (1) теңдеу мен төменгі (2) теңдеуді
(2)
пайдаланып w жоғалытқаннан кейін алынған дискырминаныт D﹙z﹚-z тің 0 ге тең болмайтын көп мүшелігі. Егер D﹙z﹚ тің нөлдік нүктесі болмаса, онда нің анықталған дәл n дана түбірі болады. Егер тағыда ді тің нөлдік нүктесі емес деп жорысақ, онда Айқындалмаған функция туралы теорема бойынша, (1) теңдеуге тиісті n дана оң анықталған функциялық элеменіттер бар болады, яғыный центірі болған мәлім бір шеңберінің ішінде ді қанағаттандырады. , әрі . Егер D﹙z﹚тің нөлдік нүктесі болатын болса, онда дің қайталанбалы түбірі болады, қайталау дәрежесін деп жорамалдайық, әрі болсын. Бүл жағдайда нүктесі тескен кішкентай шеңбер дің бойындағы n дана функциялық элеменіттер дана цикіл ге бөлінедіб жәнеде дағы қыйсық айнала ашылғанда, ұқсас бір цикілде түрған функциялық элеменіттер өзара орын алмастырады. дің дегі ашылғанда алынған көп мәнді функция болсын, онда ол белгілі шеңбер тің ішінде жинақталатын бөлшек дәрежелі қатар бүл кездегі (1) теңдеуге тиісті алгебралық функцияның элементі. болатын болса, онда оны ке алмастырамыз; ал егер болатын болса, онда оны ға алмастырамыз. Енді қысқарылмайтын теңдеу (1) ге тиісті кез -келген функциялық элементтерді (оң анықталсын, мейлі алгебралық болсын) негізе ала отырып, аналиктикалық ашу жолын пайдаланып, бүкіл фунуцияны біріктірейік, яғыный (1) теңдеуге тиісті функциялық элемент пен аналиктикалық ашу жолын қолданғанда шыққан функциялық элемент жанеде (1) тиісті болады, әрі кез-келген (1) теңдеуге тисті екі функциялық элемент аналиктикалық ашу жолы арқылы өзара келтіріліп шығарыуға болады. Сондықтан алгебралық функция дегеніміз кеңейтілген компылекіс жазықтық да тек қана санаулы алгебралық тармақтык нүктесі мен шектік нүктесіне ие толық аналиктикалық функция. Керісіншеде жоғрдағыдай қасиетке ие толық аналиктикалық функция, әрі кез-келген бір түрақты нүкте үшін, . . . Риман әдісін пайдаланып бір жаңадан қыйсық бетін алып, z бетімен алмастырайық, яғыный осы беттегі алгебралық функция әдеттегі жалғыз мәнді функция болатындай болсын, бүл бет Риман беті деп аталады . алгебралық функцияға сәйкес риман беті тығыз болады, қыисықтың кемігі алгебралық функцияның кемігі(род) болып табылады. Мысалы, супер элипістік қыйсық тің кемігі, мүндағы P(z) -z тің m дәрежелі көпмүшелігі, - нің бұтін бөлігін білдіреді. (1) теңдеумен байланысып жатқан zпен дің рационалдық функциясы тің интегіралы
Абел интегіралы деп аталады . бүл интегіралдың бірнеше нормаль формасы үшін, олардың барлығын шамалы өзгертсек барлығын солардың ішіндегі бір формаға әклуге болады. Бүл интегірал көп мәнді функция, оның көп мәнділігі тек R дің қалдығы мен тің көп мәнділігінен ғана емес, оның үстіне сәйкес Риман бетінің топологиялық қасиетіне де тәуелді. Абел интегіралын зеріттеу алгебралық функциясын бір мәнділендіру маселесіне апарып соғады. Алгебралық функцияның бір мәнділену маселесі дегеніміз (1) теңдеуде анықталғанzпен дің көп мәндік қатынасы, бір параметір арқылы ні өрнектеу, мүндағы мен лар нің ішкі өрісіT дағы t нің бір мәнді функциясы. Алгебралық функцияның бір мәнділену маселесі адеттегі бір мәнділену маселесінің дамуына тұріткі болды. 19ғ дың соңғы жартысы мен 20ғ дың алдыңғы 10 жылына дейін, әлемнің үлы математиктері, мысалға Риман, Ф. Клейн(Felix. Klein 1849~ 1925 ), Пуанкаре, және П. Кеби т. б сынды математиктер өз үлестерін қосты, соңырақ Пойнкаре мен П. Кеби 1908жылы бір уақытта шешті. Алгебралық функцияның осы бір ерекше формасының шешілуі, кезінде топология мен ортак формалық бейнелеу назариясының бірігуне апарып соқты. Алгебыралық функцияның бір мәнділігі туралы регізгі назария мынау :кемігі p=0болғандағы алгебыралық функция рационал фунуция арқылы бір мәнділенеді, яғынй бүл екуі де t ға тәуелді рационал функция; кемігі p=1 болғанда қос периодты элипістік функция арқылы бір мәнділенеді; кемігі p≥2болғанда бірлік шеңбердің ішіндегі мәлім бір Фукес тобына бағынатын
Бастауыш сыныпта математика сабақтарында оқушылардың білім деңгейін арттырудағы мұғалімні іс-әрекеті
«Еңбек пен жаңалықтар ашудың байтақ және көз жеткіліксіз қиырларына апаратын кең жол мектеп берген математикалық білімдер арқылы өтеді» - деп мектеп математикасына баға берген әйгілі ғалым Маркушевич А. И.
Адамның жеке басын қалыптастыру негізі бастауышта қаланатыны бәрімізге белгілі. «Бастауыш мектептің негізгі міндеттері - баланың жеке басының алғашқы қалыптасуын қамтамассыз ету; олардың қабілеттерін ашып, дамыту, оқуға деген ынтымақтастық тәжірибесінің берік дағдыларын меңгерту», - делінген Қазақстан Республикасының Орта білімді дамыту тұжырымдамасында. Осы міндетті ойдағыдай орындау үшін, әрбір жас балаға, оқыту, тәрбиелеу, дамыту жұмыстарын ұштастыра жүргізіп, оқушыны жан-жақты қамтамасыз етуге дайын болуымыз керек, - дейді көптеген педагогтарымыз (С. Рахметова, Ж. Адамбаева) .
Оқушыларға математика білімінің қыр-сырын жетік таныту, қабілеттерін шыңдау, кез-келген ортада өзін еркін ұстауға, Қазақстан Республикасының азаматы деген атқа лайық болатындай етіп тәрбиелеу - біздің міндетіміз болмақ. Осы орайда оқушылардың білім деңгейін арттыру - маңызды іс. Бұл мәселе көптеген жылдар бойы қарастырылып келе жатыр. «Математика, оқыту әдісіне сан алуан жетілдірулері болатындығына қарамастан, шәкірттер үшін әрдайым қиын жұмыс болып қала береді» - деген атақты ғалым Писарев Д. И. Сондықтан, матеметиканың қиындығына, күрделілігіне қарамастан, болашақ ұрпақты осы пәнге қызықтыру, білім деңгейін көтеру біз үшін орасан зор жауапкершілікті қажет ететін оқыту әдісі болуы тиіс. Бұл бастауыш сыныпта оқытуда орындалады.
Бүгінгі бөбек - ертеңгі азамат - қоғам иесі. Балғын бөбектерге ең алғаш жол көрсетуші, бағыт беруші - бастауыш мектеп мұғалімдері. Ақ жүрек балғын бөбектерге білім мен тәрбие есігін ашу бастауыш мектеп мұғалімдеріне абыройлы да жауапты жұмыс жүктейді.
Ұстаздың әрбір қылығы оқушыға әсер қалдырып, оның ары қарай жетілуіне ықпал ететіні бәрімізге белгілі. Мұғалім - оқушы атаулыға үлгі болатын өмірінің сан алуан жолынан адаспай өтуде оған бағыт беріп, жөн сілтеуші, баланы адамгершілікке, еңбек сүйгіштікке, адалдыққа және басқа да сол сияқты ізгі қасиеттерге баулитын жан.
Қазіргі заманымызда оқушының білім деңгейін көтеру мәселесі ең басты мәселелердің бірі болып отыр. Оқушының білім деңгейін көтерудегі басты тұлға - ұстаз екені бәрімізге белгілі.
Оқушының білім деңгейін көтеру дегеніміз - оқушыны жан-жақты тәрбиелеп, ғылым негіздерінен берік білім беру, болашақ қоғамға пайдалы қызмет ететін азамат етіп шығару. Оқушының бойындағы білімін ары қарай тереңдетіп, жетілдіре түсу.
Оқушының білім деңгейін көтерудегі мұғалімнің іс-әрекеті деген не?- деген сұраққа жауап іздеп көрейік.
Ғылыми-педагогикалық және психологиялық әдебиеттерді зерттеу барысында біз ең алдымен «іс-әрекет» дегеніміз не деген сұраққа жауап іздедік. Адамның психикалық өмірінің жан-жақты дамуы белгілі әрекетпен айналысуына байланысты болады. Адам өмір сүру барысында өз психикасын түрлі жолмен жарыққа шығарады.
Психология ғылымының докторы, профессор Қ. Жарықпаевтың пікірінше: «Әрекет дегеніміз түрлі қасиеттерді өтеуге байланысты белгілі мақсатқа жетуге бағытталған процесс».
«Бір мақсатқа біріккен әрекеттердің жиынтығын ғана іс-әрекет деп», - анықтама берді психолог Ф. Н. Гоноболин. Ол белгілі бір ұзақ уақытқа созылуымен сипатталады. Педагогикалық іс-әрекет туралы айтқанда біз мұғалімнің бір рет жасаған әрекетін емес, ұзақ уақыт бойы педагогтік толып жатқан қылықтары мен әрекеттерінен тұратын оның мектепке жасаған күнделікті жүйелі еңбегін айтамыз.
Сонымен, оқушылардың білім деңгейін арттырудағы мұғалімнің іс-әрекеті дегеніміз - оқушының білімін жетілдірудегі, түрлі қажеттерді өтеуге байланысты белгілі мақсатқа жетуге бағытталған процессті айтамыз. Яғни мұғалімнің сабақ үстінде оқушыға білім беру мақсатымен жүргізілетін жұмыс түрлері. Оқушылардың білім деңгейін арттырудың жолдарына тоқтала кетейік.
Ауызша есептеуге үйрету тәсілдері.
Бастауыш сынып математикасын оқыту үрдісінде есепті шығара білу шеберлігін қалыптастыру, жетілдіру және дамытудың шешуші бағыттарына тоқталайық.
1. Есеп шығаруға үйрету - математиканы оқытудағы ең қиын әрі күрделі мәселелердің бірі. Бұл балалардың шама-шарқына, психологиялық жас ерекшелігіне сәйкес салыстыру, жан-жақты талдау жасау, қарама-қарсы қою. Жалпылау, түрлендіру, зерттеу, әр алуан категорияларға біріктіру, қорытындылау, абстрактциялау сияқты түрліше меңгеруіне байланысты бірдей дәрежеде орындала бермейді.
2. Балалардың топтық, өзіндік ерекшеліктері қабілет деңгейлерінің әр түрлілігіне байланысты, олардың бәрінен де бір тарақтың жүзінен шыққандай есепті шығара білуге біркелкі үйренеді деуге болмайды.
3. Есеп шығаруға үйрету алғашқы сабақтардың өзінде-ақ басталып, сынып ілгерілген сайын бірте-бірте сәйкес шеберлік те қалыптаса бастайды.
Ауызша есептеуге үйрету бастауыш сыныптан басталатыны бәрімізге мәлім. Ол уақыт үнемдеу тұрғысынан тиімді. Бір ғана мысалдың нәтижесін бірнеше тәсілмен есептегенде берілетін түсіндірмелер, аралық нәтижелердің қалай шығатыны, ақтық нәтижеде не болатыны ауызша айтылады да, оларды жазуға уақыт жұмсалмайды. Оған қоса қай тәсілді қолдану оқушының өз еркінде болғанымен, олардың барынша тиімдісін іріктеп алуды үйретуге де мүмкіндік мол.
Математика сабағында ауызша есептеу дағдыларын қалыптастыру жұмыстарын жүргізудің маңызы зор. Сабақта оқушылардың ойлау қабілетін дамыту үшін есеп шығарғанда орындайтын амалдарды ойша шешіп алуды дағдыландырған жөн.
Бастауыш сыныпта математиканы оқыту тек математикалық білімді берумен шектелмейді. Бұл пән оқушылардың логикалық ойлауын дамытуда маңызы өте зор. Оқушылардың ойлау процесінің нақтылығын, тереңдігін анықтау үшін олардың белсенді іс-әрекетімен бірге өз бетінше жұмысын ұйымдастыру керек.
Ауызша есептеуге үйретуде оқушылардың білімі мен дағдысын тексеру кезінде арифметикалық диктант ретінде қолдануды ескеру қажет. Диктанттан кейін тексеруді ауызша жүргізген қолайлы.
Бастауыш сыныптарда математиканы оқыту мектепке сабақ және сабақтан тыс жүргізілетін сабақтар формасында жүзеге асырылады. Сабақтарда балалардың математикаға деген ынтасын арттыруға, олардың өз бетінше жұмыс істей білу дағдысын тәрбиелеуге ерекше назар аударылады. Пәнге деген ынтасы мен өз бетінше ойлай білу өзара тығыз байланысты. Сабақ балалар үшін қызықты өткенде, олардың оқу жұмысында да белсенділігі артып, өз бетінше жұмыс жасап, белсенділігін арттырғандығынан олардың пәнге деген ынтасы өседі. Оқушыларды өз бетімен ойлауға тәрбиелеп, математикаға деген ынтасын арттыру үшін оқыту әдістерін дұрыс таңдап алудың маңызы зор. Оқудың белсенді әдістерінің бірі - оқушыларға өз бетімен жұмыс істете білу.
Барлық сабақтың елеулі бөлігінде өз бетімен жұмыс істегенде оқушы жұмыстың мақсатын айқын түсіне білуі, оны орындауы, тексеруі және қателіктерді түзетуі сияқты өз бетімен істелетін жұмыстың жалпы әдістерін бірте-бірте игеріп алуы тиіс.
Оқушылардың сабақта өздігінен орындайтын жұмыстарын тиімді ұйымдастыру үшін математика кабинеттерінде дидактикалық материалды, үлестірмелі материалдар, баспа негіздегі дәптерлер, тағы басқа оқу құралдары жинастырылуы қажет. Дегенмен оқушыларға оқулықпен жұмыс істеуді үйретудің орны ерекше. Барлық ғылыми-техникалық білімнің көзі - кітапқа, оның ішінде оқулыққа оқушылардың сүйіспеншілігі мен құрметін арттыру, олармен өздігінен жұмыс істеуді үйрету мұғалімнің басты міндетінің бірі. Әр сынып оқулықтары қажетіне орай орындалуға тиісті жаттығулармен, есептермен, практикалық тапсырмалармен, суреттермен қамтамассыз етілген. Өздігінен жұмыс істеуді оқушылардың сабақ үстіндегі қызметіне енгізу сабақтың құрылымына да, элементтеріне де әсерін тигізеді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz