Функцияның үздіксіздігі мен монотондылығы және күрделі функцияның туындысы


Мазмұны
Кіріспе
I. Функцияның үздіксіздігі, монотондылығы
II. Күрделі функцияның туындысы
Қорытынды
Пайдаланған әдебиеттер тізімі
Кіріспе
Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Математика (грекше: μάθημα - ғылым , білім , оқу ; μαθηματικός - білуге құштарлық ) - әлемнің сандық қатынастары мен кеңістік формалары, оның ішінде құрылымдар, өзгерістер, белгісіздік жөніндегі ғылым. Ол абстрактілендіру және логикалық қорыту, есептеу, санау, өлшеу және физикалық нәрселерді жүйелі түрде орнықтыру, бейнелеу мен өзгерістерді оқыту арқылы көрініс табады. Математиктер жаңа тұжырымдамаларды сипаттайтын осы түсініктерді ретімен таңдалып алынған аксиомалар мен анықтамаларды пайдалана отырып, қорыта зерттейді.
Бұл жұмыс алгебра курсында қарастырылатын функцияның монотондылығы мен туындысы және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.
«Функцияның монотондылығы мен туындысы» мектептегі алгебра және анализ бастамалары курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с. с. мазмұнды есептердің шығарылуы квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т. б. жағдайларда квадрат теңдеулерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.
Функцияның үздіксіздігі, монотондылығы
Теорема . Егер f`(x) функциясы белгілі бір шекті не шексіз аралықта анықталған үздіксіз монотонды функция болып, осы аралықта жатқан екі х=а және х=в нүктелерінде қабылдайтын мәндері әр түрлі f(а) =A, f(в) =B болса, онда осы мәндердің арасында жатқан кез келген С саны үшін, функцияның мәні -осы санға тең болатындай f(x) =С аралықтың ішінде жатқан тек бір ғана
нүктесі табылады.
Үздіксіз функцияның осы қасиеттерін пайдаланып f(x) =С, (мұндағы f анықталу облысында үздіксіз функция ) теңдеуінің нақты шешімдерінің санын анықтауға болады . Ол үшін біз мынандай амалдарды біртіндеп орындауымыз қажет.
1) f функциясының анықталу облысын табамыз.
Айталық D(f) =[a, b] болсын.
2) y=f(x) анықталу облысында үздіксіз және монотондылыққа зерттеп алғаннан кейін f функциясының мәндерінің облысы Е(f) =[A=f(x) ; B=f(x) ]
анықтаймыз.
3 ) Енді
орындалатындығын тексереміз. Сонда үздіксіз монотонды функцияның жоғарыдағы қасиетіне сәйкес берілген теңдеудің тек бір ғана шешімі болады . Бұл шешімді практикада «іріктеп алу»әдісімен тапқан қолайлы.
4) Ал егерде
шарты орындалатын болса, онда теңдеудің нақты шешімдері болмайды.
Сонымен мынандай қорытынды шығаруға болады. Егерде берілген теңдеулердің сол жағында тұрған сан осы теңдеудің мәндерінің облысында жататын болса, онда f функциясының мәндерінің облысында жататын болса, онда f үздіксіз. Монотонды функция болғанда, теңдеудің тек бір ғана нақты шешімі бар болады . Бұл шарт орындалмаған жағдайда теңдеудің нақты шешімі болмайды.
Демек, үздіксіз монотонды функцияның жоғарыдағы қасиетіне сүйеніп, берілген теңдеуді шешпестен бұрын бірден анықтауымызға болады.
1-мысал . Теңдеудің нақты шешімдерін анықтау керек .
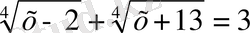
Шешуі : Теңдеуді Ньютон -биномы формуласын қолданып, дәрежелеу арқылы шығаратын болсақ, онда күрделі радикалы бар бес мүшесі бар теңдеу келіп шығады. Демек, берілген теңдеуді түбірден құтқару әдісімен шешу мүмкін емес.
Егерде берілген теңдеуді көмекші белгісіз енгізу әдісі арқылы шығаратын болсақ, онда төртінші дәрежелі мынадай рационал теңдеулер жүйесі келіп шығады:
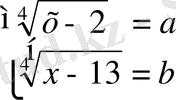
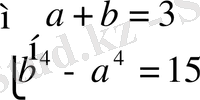
Демек, бұл теңдеуді бұл әдіспен шығару да қолайсыз.
Бұл теңдеуді функциялық әдіспен шығару әлдеқайда жеңілдеу.
Теңдеуді функциялық әдіспен шешу үшін
y=
+
функциясын қарастырамыз. Бұл функция
аралығында анықталған үздіксіз монотонды өспелі функция.
Бұл функция өзінің ең кіші мәнін аргументіннің х=2-ге тең болатын мәнінде қабылдайды:y min =y
=
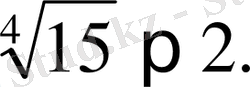
Сондықтан
Сонымен бірге, мұнда
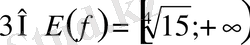
Демек, үздіксіз монотонды функцияның жоғарыдағы қасиетіне сәйкес
теңдеуінің бір ғана нақты шешімі бар болады.
Теңдеудің бір ғана шешімінің x=3екендігін байқау қиын емес, өйткені
1+2=3 Жауабы: x=3
2-мысал
. Теңдеуді шеш:
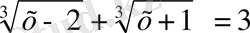
Теңдеуді функциялық әдіспен шешу үшін у=
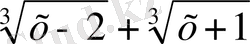 функциясын қарастырамыз . Бұл функция
функциясын қарастырамыз . Бұл функция
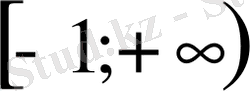 интервалында анықталған үздіксіз монотонды өспелі функция. у функциясы өзінің ең кіші мәнін аргументтің x=-1-ге тең болатын мәнінде қабылдайды :
интервалында анықталған үздіксіз монотонды өспелі функция. у функциясы өзінің ең кіші мәнін аргументтің x=-1-ге тең болатын мәнінде қабылдайды :
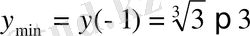 ;
;
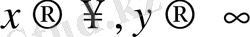 . Бұдан
. Бұдан
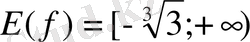 . Сонымен бірге, мұнда
. Сонымен бірге, мұнда
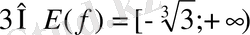 . Демек үздіксіз монотонды функцияның жоғарыдағы қасиетіне сәйкес
. Демек үздіксіз монотонды функцияның жоғарыдағы қасиетіне сәйкес
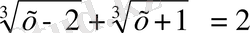 теңдеуінің бір ғана нақты шешімі x=3 бар болады
. Жауабы: x=3
теңдеуінің бір ғана нақты шешімі x=3 бар болады
. Жауабы: x=3
3-мысал .
Теңдеуді шеш:
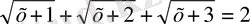
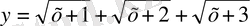 функциямыз [-1; +
функциямыз [-1; +
 арлығында үздіксіз және монотонды өспелі функция . бұл функция өзінің ең кіші мәнін аргументтің х=-1ге тең болатын мәнінде қабылдайды:
арлығында үздіксіз және монотонды өспелі функция . бұл функция өзінің ең кіші мәнін аргументтің х=-1ге тең болатын мәнінде қабылдайды:
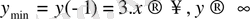 , бұдан
, бұдан
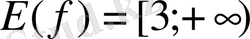 . Сонымен бірге, мұнда 2
. Сонымен бірге, мұнда 2
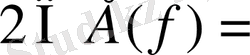 [3; +
[3; +
 Демек, үздіксіз монотонды функцияның қасиетіне сәйкес берілген теңдеудің нақты шешімдері болмайды.
Жауабы :
Демек, үздіксіз монотонды функцияның қасиетіне сәйкес берілген теңдеудің нақты шешімдері болмайды.
Жауабы :
 .
.
Тест .
1. Теңдеуді шешіңіз:
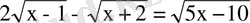 .
.
A) 1. B) 4. C) 6. D) 5. E) 2.
2.
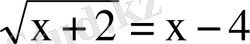 теңдеуінің шешімі жатқан аралық
теңдеуінің шешімі жатқан аралық
A) (3; 7] B) (-5; 5) C) [-7; 1) D) [-4; 2) E) [-3; 1)
3. Теңдеуді шешіңіз:
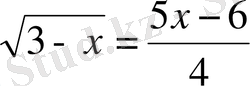 .
.
A) 2. B) 4. C) 0. D) 5. E) 1.
4 . Теңдеулер жүйесін шешіңіз:
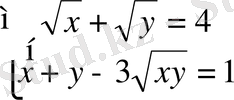
A) (-1; -9), (-9; -1) . B) (0; 1), (1; 0) . C) (16; 2), (2; 16) .
D) (1; 9), (9; 1) . E) (2; 8), (8; 4) .
5.
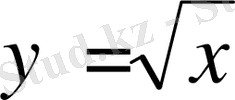 функциясының графигі мына нүкте арқылы өтеді:
функциясының графигі мына нүкте арқылы өтеді:
A) K (-400; 20) B) Q (-900; 30) C) M (121; 11)
D) P (25; -5) E) N (81; -9)
Оқушыларға тестпен бірге тексеру кестесі таратылады :
Дұрыс жауаптары
Тест жұмыстары инемен тесу әдісімен тексеріліп бірден жауабы айтылады.
КҮРДЕЛІ ФУНКЦИЯНЫҢ ТУЫНДЫСЫ
а) Туындының көмегімен күрделі теңдеулерді шешуге, физикада жылдамдық пен үдеуді есептеуге, геометрияда жанаманың теңдеуін анықтауға және де білімнің басқа салаларында да пайдаланылады .
Осы уақытқа дейін элементар функциялардан туынды алып үйрендік . Бүгінгі сабақта күрделі функция ұғымымен және оның туындысын есептеу формуласын пайдаланып есептер шығаруды үйренеміз.
б) Күрделі функция деп y=f(u) : u€U; y€Y u=g(x) x€X
y=f(g(x) ) функциясы аталады.
y= f(g(x) ) күрделі функцияның жалпы түрі
u=g(x) күрделі функцияның ішкі бөлігі, ал y=f(u) сыртқы бөлігі деуге болады.
Енді күрделі функцияның ішкі және сыртқы бөлігін ажыратуға бірнеше мысал келтірейік:
y=f(u) u=g(x)
1. u=
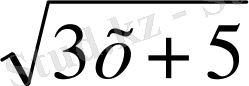 3х+5 функцияның ішкі бөлігі; y=
3х+5 функцияның ішкі бөлігі; y=
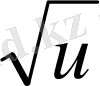 фунцияның сыртқы бөлігі
фунцияның сыртқы бөлігі
2. y=sin(3x-
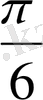 ) 3x-
) 3x-
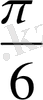 функцияның ішкі бөлігі; y=sinu фунцияның сыртқы бөлігі
функцияның ішкі бөлігі; y=sinu фунцияның сыртқы бөлігі
3. y=
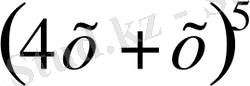
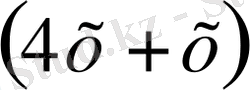 функцияның ішкі бөлігі; y=u
5
фунцияның сыртқы бөлігі
функцияның ішкі бөлігі; y=u
5
фунцияның сыртқы бөлігі
Күрделі функцияның туындысытабу ережесі:
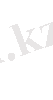
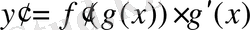
Осы формуланы пайдалануға мысал келтірейік:
y=(5+2x
3
)
7
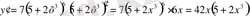
y
=
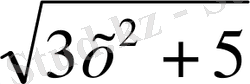
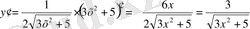
iV. Жаңа сабақты бекіту Күрделі функцияның туындысын табу жұмыртқаның бөліктері ретінде қарастырып,
сыртқы бөлігінен туынды алу, «қабығын ашу» ретінде қарастыру бірақ ақ уызы мен сары уызы өзгеріссіз қалады, яғни:
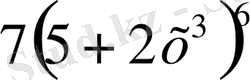
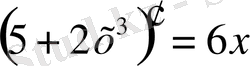
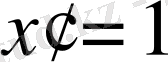
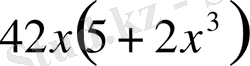
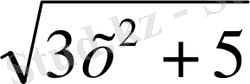
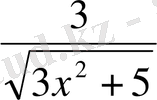
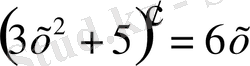
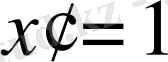
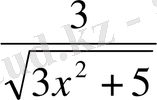
V . Жаттығу есептерін шығару
. №213(а, б) №214(а, б) №215(а, б)
№ 213 Күрделі функциясын құрайтын функцияларды анықта:
a) y=(x+3) 2 ; х+3 функцияның ішкі бөлігі; y=u 2 фунцияның сыртқы бөлігі
б) y=cos(x+
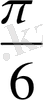 ) u=x+
) u=x+
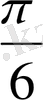 функцияның ішкі бөлігі; cosu фунцияның сыртқы бөлігі
функцияның ішкі бөлігі; cosu фунцияның сыртқы бөлігі
№214 Элементар функциялардан тұратын күрделі функция жазу керек:
а) f(x) =sinx ; g(x) = 5x y=sin 5x немесе y=5sinx
б ) f(x) =tgx ; g(x) = 7x+1 y=7tgx+1 немесе y=tg(7x+1)
№216 Функцияның туындысын тап:
а) y=
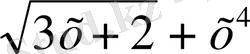 Equation. 3
Equation. 3
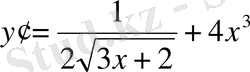 Equation. 3
Equation. 3
б)
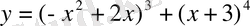 Equation. 3
Equation. 3
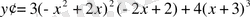 Equation. 3
Equation. 3
№217 Функцияның туындысын тап:
а)
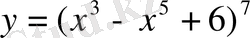
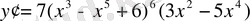 Equation. 3
Equation. 3
б)
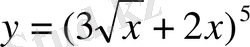
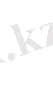
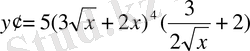
VI. Тест алу
1. Функцияның туындысын табыңыз: f(x) = x
5
- 2
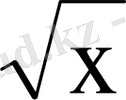 .
.
A) 5x 4 -
. B) 5x 4 -
. C) 5x 4 +
. D) 5x 4 -
. E) 5x 4 -
.
2. f(х) = 3х
2
+ 10
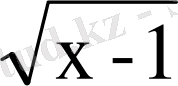 функциясы берілген. f′(х) табыңыз.
функциясы берілген. f′(х) табыңыз.
A) 6х -
. B) 6х -
. C) 6х +
. D) 6х -
. E) 6х +
.
3. f(x) = (x+2) 3 +
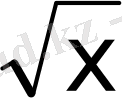 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
A) 3(x+2) 2 +
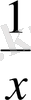 . B) x +
. B) x +
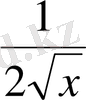 . C) 3(x+2) 2 +
. C) 3(x+2) 2 +
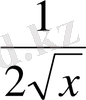 D) 3(x+2) + 2
D) 3(x+2) + 2
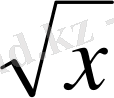 . E) 3x2 + 2
. E) 3x2 + 2
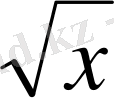 .
.
4. Функцияның туындысын табыңыз у = x 8 - 3x 6 + 2x 3 - 7.
A) 8x
7
+ 18x
5
- 6x. B) 8x
7
- 18x
5
+ 6x. C) x
9
- 3x
7
+ 2x
4
. D) 8x
7
- 18x
5
+ 6x
2
. E)
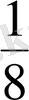 x
7
-
x
7
-
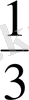 x
5
+
x
5
+
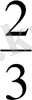 x
2
.
x
2
.
26. y = (x 2 + 1) 6 функциясының туындысын табыңыз.
A) (x 2 + 2х + 1) B)
. ь C) (x - 1) 5 D)
. E) 12х(x 2 +1) 5
Жауабы:А; В; С; Д; Е.
ҚОРЫТЫНДЫ
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz