Математикалық теңдеулер жүйесі

Мазмұны

Кіріспе

1. Көрсеткіштік теңдеулер
2. Қарапайым логарифмдік теңдеулер
3. Логарифдік теңдеулерді шешу әдістері

Қорытынды

Пайдаланған әдебиеттер тізімі

Кіріспе

Бірдей негізге келтіру арқылы шығарылатын теңдеу.

1. ax=b ( a>0, a≠1)

Егер b>0 болса, теңдеудің жалғыз ғана түбірі бар болады.

Егер b≤0 болса, теңдеудің түбірі жоқ болады.

2. af(x) =ag(x) мұндағы (a>0, a≠1) теңдеуінің сол және оң бөліктерінің

негіздері бірдей болғандықтан, a ^f(x) =a ^g(x) теңдеуі f(x) =g(x) теңдеуімен мәндес болады.

Мысал: 5 ^x =125

Шешуі:, 125>0, 125=5 ³ , 5 ^x =5 ³ , x=3 Жауабы: 3

Мысал: 2 ^x-1 =1

Шешуі: 2 ^x-1 =2 ⁰ , x-1=0, x=1 Жауабы:1

Мысал: $\frac{{0, 2}^{x - 0, 5}}{\sqrt{5}}\ \$ $\frac{{0, 2}^{x - 0, 5}}{\sqrt{5}}\ \$ = 5∙ ${0, 04}^{x - 1}$ ${0, 04}^{x - 1}$

Шешуі: барлық дәрежелерді бір ғана 5негізге келтіреміз.

Сонда 5 ^{0, 5-x} ∙5 ^{-0, 5} =5∙5 ^-2x+2 теңдеуін аламыз, оны 5 ^-x =5 ^-2x+3 түріне түрлендіреміз де, дәреже көрсеткіштерін теңестіріп, теңдеуді шешеміз:

-x= -2x+3, x=3 Жауабы: 3

Жаңа айнымалы енгізу арқылы жиі шығарылатын теңдеулер.

1. A∙a2x+B∙ax+C=0 a>0, a≠1

a ^x =y, y>0 деп белгілесек, у-ке қатысты квадрат теңдеуге келеді. Ay ² +By+C=0

Мысал: 5 ^2x -6∙5 ^x +5=0

Шешуі: 5 ^x =y, y>0 белгілесек у-ке байланысты y ² -6y+5=0 квадрат теңдеуіне келеміз. Бұдан y ₁ =1, y ₂ =5 екенін табамыз.

у-тің екі мәніне сәйкес екі көрсеткіштік теңдеу шығады.

1. 5x=1, x=0
2. 5x=5, x=1

Бұл теңдеулерден есептің екі жауабы шығады. Жауабы: 0; 1

2) A∙a ^x +B∙a ^-x +C=0 a ^x =y (y>0) деп белгілесек,

Ay ² +Cy+B=0 квадрат теңдеуге келеміз.

Мысал: 5 ^x -24=25∙5 ^-x

Шешуі: 5 ^x =y, y ² -24y-25=0 квадрат теңдеуге келеміз.

y>0

y ₁ = -1; y ₂ =25 у -тің таңбасын ескере отырып теңдеуді шешсек,

1. 5x= -1 (бұл теңдеудің нақты түбірі жоқ), өйткені кез келген х€R үшін 5x>0
2. 5x=25, 5x=52, x=2 Жауабы: 2
3. A∙a2x+B(a∙b) x+C∙b2x=0

Егер теңдеудің барлық мүшелерін b ^2x ≠0, өрнегіне бөлсек мынадай түрге келеміз: A∙ $\left( \frac{a}{b} \right) ^{2x} + \ B \bullet \left( \frac{a}{b} \right) ^{x} + \ C = 0, \$ $\left( \frac{a}{b} \right) ^{2x} + \ B \bullet \left( \frac{a}{b} \right) ^{x} + \ C = 0, \$ $\left( \frac{a}{b} \right) ^{x} = y, \ (y > 0)$ $\left( \frac{a}{b} \right) ^{x} = y, \ (y > 0)$ деп белгілесек, у-ке байланысты Ay ² +By+C=0 теңдеуге келеміз.

Мысал: 6∙3 ^2x -13∙6 ^x +6∙2 ^2x =0

Шешуі: 6∙3 ^2x -13∙(2∙3) ^x +6∙2 ^2x =0, 6 ^x =(2∙3) ^x =2 ^x ∙3 ^x теңдеуді шешу үшін екі жағын 2 ^2x ≠0 бөлеміз.

6∙ $\left( \frac{3}{2} \right) ^{2x}$ $\left( \frac{3}{2} \right) ^{2x}$ - 13∙ $\left( \frac{3}{2} \right) ^{x}$ $\left( \frac{3}{2} \right) ^{x}$ + 6 = 0; $\left( \frac{3}{2} \right) ^{x}$ $\left( \frac{3}{2} \right) ^{x}$ = y, (y>0) деп белгілесек у-ке байланысты квадрат теңдеу шығады.

6y ² -13y+6=0

y ₁ = $\frac{3}{2}$ $\frac{3}{2}$ ; y _{2 =} $\frac{2}{3}$ $\frac{2}{3}$

1. (32) x\left( \frac{3}{2} \right) ^{x}(32) x\left( \frac{3}{2} \right) ^{x}=32\ \frac{3}{2}32\ \frac{3}{2}, x=1
2. (32) x\left( \frac{3}{2} \right) ^{x}(32) x\left( \frac{3}{2} \right) ^{x}=32\ \frac{3}{2}32\ \frac{3}{2}, , x=-1

Жауабы: -1; 1

Кейде көрсеткіштік функцияны ортақ көбейткіш ретінде жақша сыртына шығару арқылы шешкен тиімді болады.

Мысал: 5 ^x +5 ^x+2 =26

Шешуі: 5 ^x (1+5 ² ) =26

5 ^x ∙26=26

5 ^x =1

x=0 Жауабы: 0

Графиктік тәсілмен шығарылатын теңдеулер.

a ^φ(x) =f(x) түріндегі теңдеулер

Ал мұндай теңдеулер түбірлерінің жуық мәндерін графиктік тәсілмен табуға болады.

a ^x =b a>0, a≠1, b>0

y=b түзуі y=a ^x функциясының графигін бір ғана нүктеде қиып өтеді. Қиылысу нүктесінің абсциссасы берілген көрсеткіштік теңдеудің түбірі болады.

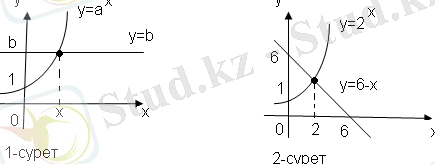
Мысал: 2 ^x =6-x

Шешуі: y=6-x түзуі y=2 ^x функциясының графиктерін сызып, олардың қиылысу нүктесінің абсциссасын табайық. Екі графиктің қиылысу нүктесінің абсциссасы x=2.

Жауабы: 2

Негіздері әр түрлі болып келген көрсеткіштік теңдеулерді шешу мысалдары.

Мысал: 2 ^x =3 ^x

Шешуі: 3 ^x >0, $\left( \frac{2}{3} \right) ^{x}$ $\left( \frac{2}{3} \right) ^{x}$ =1, $\left( \frac{2}{3} \right) ^{x}$ $\left( \frac{2}{3} \right) ^{x}$ = $\left( \frac{2}{3} \right) ^{0}$ $\left( \frac{2}{3} \right) ^{0}$ , x=0 Жауабы: 0

Мысал: $\left( \sqrt{2 + \sqrt{3}} \right) ^{x}$ $\left( \sqrt{2 + \sqrt{3}} \right) ^{x}$ + $\left( \sqrt{2 - \sqrt{3}} \right) ^{x}$ $\left( \sqrt{2 - \sqrt{3}} \right) ^{x}$ =4

$\sqrt{2 - \sqrt{3}}$ $\sqrt{2 - \sqrt{3}}$ = $\ \ \frac{\sqrt{\left( 2 - \sqrt{3} \right) }\ \ \ \ \sqrt{\left( 2 + \sqrt{3} \right) }\ \ \ }{\sqrt{2 + \sqrt{3}}}\$ $\ \ \frac{\sqrt{\left( 2 - \sqrt{3} \right) }\ \ \ \ \sqrt{\left( 2 + \sqrt{3} \right) }\ \ \ }{\sqrt{2 + \sqrt{3}}}\$ = $\frac{1}{\sqrt{2 + \sqrt{3}}}$ $\frac{1}{\sqrt{2 + \sqrt{3}}}$

$\left( \sqrt{\mathbf{2 +}\sqrt{\mathbf{3}\mathbf{\ }}} \right) ^{\mathbf{x}}$ $\left( \sqrt{\mathbf{2 +}\sqrt{\mathbf{3}\mathbf{\ }}} \right) ^{\mathbf{x}}$ + $\left( \frac{\mathbf{1}}{\mathbf{2 +}\sqrt{\mathbf{3}}} \right) ^{\mathbf{x}}$ $\left( \frac{\mathbf{1}}{\mathbf{2 +}\sqrt{\mathbf{3}}} \right) ^{\mathbf{x}}$ = 4, $\left( \sqrt{\mathbf{2}\mathbf{+}\sqrt{\mathbf{3}}} \right) ^{\mathbf{x}}\mathbf{\ }\mathbf{\ }$ $\left( \sqrt{\mathbf{2}\mathbf{+}\sqrt{\mathbf{3}}} \right) ^{\mathbf{x}}\mathbf{\ }\mathbf{\ }$ = y, (y>0) деп белгілесек

y + $\ \frac{1}{y}$ $\ \frac{1}{y}$ = 4, y ² - 4y + 1= 0, y _{1, 2} =2 ± $\ \sqrt{3}$ $\ \sqrt{3}$

1. (2+3) x\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}(2+3) x\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}= 2 +3\ \sqrt{3}3\ \sqrt{3}

$\frac{x}{2}$ $\frac{x}{2}$ = 1, x = 2

2. (2+3) x\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}(2+3) x\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}= 2−3- \ \sqrt{3}−3- \ \sqrt{3}

$\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}$ $\left( \sqrt{2 + \sqrt{3\ }} \right) ^{x}$ = $\frac{1}{2 + \sqrt{3}}$ $\frac{1}{2 + \sqrt{3}}$

$\frac{x}{2}$ $\frac{x}{2}$ = -1, x = -2

Жауабы: $\{ - 2; 2\}$ $\{ - 2; 2\}$

Мысал: 7 ^х-4 = 10 ^x-4 , Шешуі: теңдіктің екі жағын 10 ^х-4 -ке бөлеміз

$\left( \frac{7}{10} \right) ^{x - 4}$ $\left( \frac{7}{10} \right) ^{x - 4}$ = 1, $\left( \frac{7}{10} \right) ^{x - 4}$ $\left( \frac{7}{10} \right) ^{x - 4}$ = ${\ \left( \frac{7}{10} \right) }^{0}$ ${\ \left( \frac{7}{10} \right) }^{0}$ , x-4=0, x=4 Жауабы: 4

Оқулықпен жұмыс: № 168; № 176; № 177

Көрсеткіштік теңдеулерді шешу икемдіктерін тексеру / тест /

I топ

1. 9x- 4∙3x-45=0

1. 5 B) 2 C) -5 D) 9 E) 7

2. 5x+1+ 2∙5x= 175

1. 1 B) 15\frac{1}{5}15\frac{1}{5}C) 0 D) 4 E) 2

3. 4x- 10∙2x-1- 24 = 0

1. 3, 8 B) -3, 8 C) 8 D) -3; 3 E) 3

4. 8x-3= 9x-3

1. 4 B) 3 C) 2 D) 1

5. 3x\sqrt{3^{x}}3x\sqrt{3^{x}}∙4x\sqrt{4^{x}}4x\sqrt{4^{x}}= 36

1. 2 B) 4 C) 1 D) -1

6. 5x-1+ 5x-2+ 5x-3= 155

1. 0 B) 2 C) 625 D) 1, 24 E) 4

7. 125 ∙ 25x- 70 ∙10x+ 8∙4x=0

1. 1; 1 B) -2; -1 C) 2; 2 D) -3; 3 E) (-1; 1)

II топ

1. 121x-2∙11x+1 = 0

1. 2 B) 3 C) 1 D) 0 E) 6

2. 2x+4+ 3∙2x= 76

1. 2 B) 4 C) 3, 5 D) 4, 5 E) 3

3. 4x+ 2x+1- 24 = 0

1. -2; 6 B) 2 C) 2; -6 D) -4; 6 E) 4; -6

4. 2x-4= 5x-4

1. 4 B) 3 C) 2 D) 1

5. 2x3\sqrt[3] {2^{x}}2x3\sqrt[3] {2^{x}}∙3x3\sqrt[3] {3^{x}}3x3\sqrt[3] {3^{x}}= 216

1. 3 B) 9 C) 1 D) 0

6. 3x+ 3x+1+3x+2+3x+3= 360

1. 2 B) -2 C) 4 D) 1 E) 3

7. 7∙49x+ 5∙14x= 2∙4x

1. Ø B) -0, 5 C) -1 D) 1 E) 0, 5

Деңгейлік тапсырмалар (тақтада орындалады)

I топ

А деңгейі

9 ^x+1 + 9 ^2x-1 = 54 ∙ 27 ^x-1

Жауабы: х=2

В деңгейі

4 ^{2x - 3x +3} = 24 - 12 + 6 - 3 + …

Жауабы: $\ \frac{1}{2}$ $\ \frac{1}{2}$ ; 1

С деңгейі

8 ^x+1 + 8∙(0, 5) ^3x + 3∙2 ^x+3 = 125-24∙(0, 5) ^x

Жауабы: x ₁ = 1, x ₂ = -2

II топ

А деңгейі

2 ^x+2 -2 ^x+3 - 2 ^x+4 = 5 ^x+1 - 5 ^x+2

Жауабы: 0

В деңгейі

5 ^│4x-6│ = 25 ^3x-4

Жауабы: 1; 4

С деңгейі

12 ^x + 5 ^x = 13 ^x

Жауабы: 2

Қарапайым логарифмдік теңдеулер

Ең қарапайым логарифмдік теңдеуді қарастырайық

log _а х=в ; а>0, a=1, x>0.

Санның логарифмнің анықтамасынан а ^в саны сол шешімі екендігі бірден табылады, яғни х= а ^в

І-әдіс. Логарифмдік теңдеуді логарифмнің анықтамасы бойынша log _а х=в

түбірін табамыз х= а ^в .

Логарифмдік теңдеулерді шешуді анықталу облысынан бастау керек, өйткені

бөгде түбірлері пайда болу мүмкін.

1-мысал . Теңдеуді шеш.

log ₂ (х ² +4х+3) =3

Анықталу облысы: х ² +4х+3>0

х ₁ =-1, х ₂ = -3

Енді, х ² +4х+3=2 ³

х ² +4х+3-8 =0

х ² +4х-5=0

х ₁ =-5, х ₂ =1 Ж/ы: -5; 1.

ІІ-әдіс. Логарифмдік теңдеулерді log _а f(х) = log _a g(х) түріне келтіріп шешеді.

Бұл теңдеу f(х) = g(х) теңдеуіне мәндес болады, қосымша f(х) >0, g(х) >0.

Бұл әдісті потенцирлеу әдісі дейді.

2- мысал.

log ₅ (2х+3) = log ₅ (х+1)

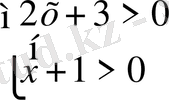
Анықталу облысы: Equation. 3 Equation. 3 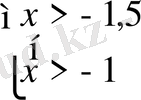Equation. 3 x >-1

Онда 2х+3=х+1

2х-х=1-3

х=-2

Тексеру: log ₅ (2(-2) +3) = log ₅ (-2+3)

log ₅ (-1) = log ₅ (-1) - мағынасы жоқ( анықтамасы бойынша х>0)

және анықталу облысы бойынша x >-1, ал бізде х= -2 <-17

Сондықтан шешімі жоқ.

ІІІ-әдіс.

3- мысал.

Log ² ₅ х- log 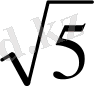х - 3=0 Анықталу облысы: х>0

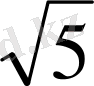=5 ^1/2 ,

Log ² ₅ х- log ₅ ^1/2 х - 3=0

Логарифмнің қаситі бойынша

Log ² ₅ х- 2 log ₅ х-3=0 log ₅ х=-1 log ₅ х=3

Жаңа шама енгіземіз log ₅ х=у х=5 ^-1 х=5 ³

у ² -2у-3=0 х=1/5 х=125

у ₁ =- 1, у ₂ =3 Ж/ы: 1/5; 125

Бұл жағдайда, жаңа айнымалы енгізу арқылы, квадраттық теңдеуге келтіріп шештік.

Сонымен қатар, логарифмдік теңдеулерді түрлендіру барысында олардың тең шамалылығын қадағалай отырып, логарифмнің қасиеттерін де қолдану керек.

4-мысал.

Log ₃ (х+3) + log ₃ (х+1) =1

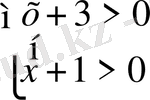
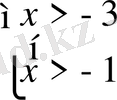
Анықталу облысы: x > -1

Log ₃ (х+3) (х+1) = 1

Log ₃ (х ² +4х+3) =1

x ² +4x +3 =3 ¹

x ² +4x =0

x ₁ =1, x ₂ = -4 Ж/ы : 1.

4. Тест тапсырмалары .

А деңгейі.

1. Log ₂ х =4

А) 14 ; в) 4 с) 16 д) 2

2. Log ₅ (2х-1) =2

А) 15 ; в) 13 с) 26 д) 14

В деңгейі.

1. Log ₇ (4х-6) = Log ₇ (2х-4)

А) 1 ; в) шешімі жоқ; с) -1 д) -2

2. . Log _1/2 (2х+6) = -3

А) -1; в) 1 с) -2 д) 3

С деңгейі .

... жалғасы

Алгебралық теңдеулер жүйесінің анықтамасы

Функцияларды енгізу терезесі

Орта мектепте алгебралык тендеулер мен тенсіздіктер такырыптарын окыту әдістемесі

Зерттеу процессі кезіндегі экспериментті жоспарлау әдістері

Мектеп математика курсындағы теңдеулер мен теңсіздіктерді оқыту әдістемесі

Мектепте алгебралық және геометриялық материалдарды қабылдау мен меңгеру ерекшеліктері

“Алгебралық сызықтық теңдеулер жүйесін шешу” тақырыптары бойынша дәрістік, зертханалық сабақтарды жүргізуде қолданылатын әдістемелік құрал жасау

Математиканы оқыту әдістемесінің жалпы мәселелерімен таныстыру

Математикалық модельдеу бойынша дәрістер

Сызықтық программалау есептерінің тәжірибелік есептерінің математикалық моделі

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс