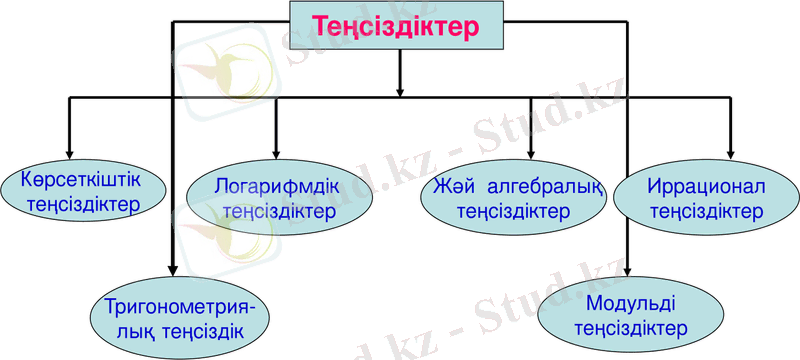
Теңсіздіктер: ұғымы, түрлері және шешу әдістері


Мазмұны
Кіріспе
- Теңсіздіктер ұғымы
- Теңсіздіктер қасиеттері
- Күрделі теңсіздіктерді шешу әдістері
Қорытынды
Пайдаланылған әдебитеттер тізімі
Кіріспе
Теңсіздіктер ұғымы
Анықтама.
«>», «<», «
 », «
», «
 » белгілерімен байланысқан өрнектер теңсіздіктер деп аталады.
Теңсіздіктерді шешу дегеніміз
-теңсіздікті қанағаттандыратын және оған кіретін белгісіздердің мәндер жиынын табу.
» белгілерімен байланысқан өрнектер теңсіздіктер деп аталады.
Теңсіздіктерді шешу дегеніміз
-теңсіздікті қанағаттандыратын және оған кіретін белгісіздердің мәндер жиынын табу.
Бір айнымалысы бар теңсіздіктерді қарастырамыз:
ƒ(х) <
 (x) (1)
(x) (1)
Егер D(ƒ) жиыны ƒ(х) функциясының, ал D(
 ) жиыны
) жиыны
 (x) функция-
(x) функция-
сының анықталу облысы болса, онда D=D(ƒ)
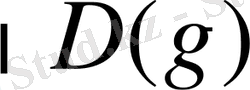
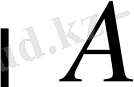 жиынын (1) теңсіздіктің
мүмкін мәндер жиыны
(ММЖ) деп атаймыз. Мұнда А жиынының құрамына (1) теңсіздіктің мағынасы болатындай х-тің барлық мәндері жиыны енеді.
жиынын (1) теңсіздіктің
мүмкін мәндер жиыны
(ММЖ) деп атаймыз. Мұнда А жиынының құрамына (1) теңсіздіктің мағынасы болатындай х-тің барлық мәндері жиыны енеді.
Шешімдер жиындары бірдей екі теңсіздікті тең шамалы теңсіздіктер деп атайды.
Мысал: х-2<4-x және х-2+х 2 <4-x+x 2 теңсіздіктері тең шамалы. Себебі, бұл теңсіздіктердің екеуінің де шешімдер жиыны (-∞; 3) болады.
Модульмен берілген теңсіздіктер:
1.
 түрінде берілсе, онда:
түрінде берілсе, онда:
а) егер
 болса, онда теңсіздіктің шешімі жоқ;
болса, онда теңсіздіктің шешімі жоқ;
б) егер
 онда теңсіздіктің шешімі
онда теңсіздіктің шешімі
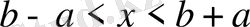 .
.
2.
 түрінде берілсе, онда:
түрінде берілсе, онда:
а) егер
 болса, онда
болса, онда
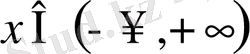 кез келген нақты сан;
кез келген нақты сан;
б) егер
 болса, онда
болса, онда
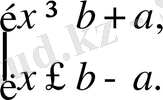
3.
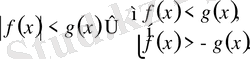
4.
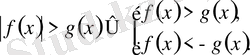
5.
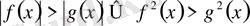 .
.
Иррационал теңсіздіктер:
1.
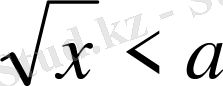 түрінде берілсе, онда шешім :
түрінде берілсе, онда шешім :
а) егер
 болса, онда теңсіздіктің шешімі жоқ;
болса, онда теңсіздіктің шешімі жоқ;
б) егер
 онда шешім
онда шешім
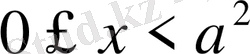 болады;
болады;
2.
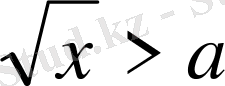 түрінде берілсе, онда шешім :
түрінде берілсе, онда шешім :
а) егер
 онда шешім
онда шешім
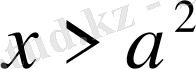 болады;
болады;
б) егер
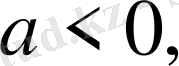 онда шешім
онда шешім
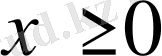 болады;
болады;
в) егер
 онда шешім
онда шешім
 болады;
болады;
3.
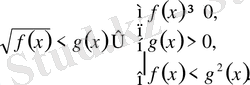 4.
4.
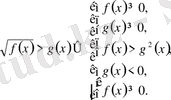
5.
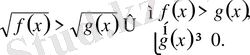
Белгісіздері радикал таңбасы астында болып келетін теңсіздіктерді иррационал теңсіздіктер деп атайды.
1.
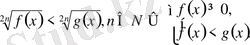
2.
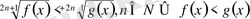 .
.
3.
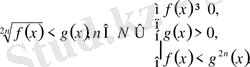
4.
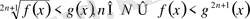 .
.
5.
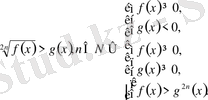
(5 екі теңсіздіктер жүйесіне эквивалентті) .
6.
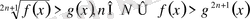 .
.
Көрсеткіштік теңсіздіктер:
1.
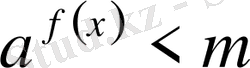 түрінде берілсе:
түрінде берілсе:
а) егер
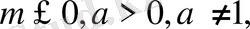 онда шешім жоқ;
онда шешім жоқ;
б) егер
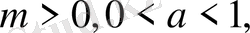 онда шешім
онда шешім
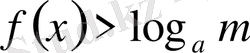 ;
;
в) егер
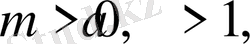 онда шешім
онда шешім
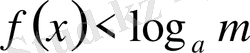 болады.
болады.
2.
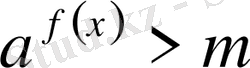 түрінде берілсе:
түрінде берілсе:
а) егер
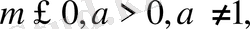 онда шешімі
онда шешімі
 , яғни
, яғни
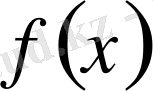 функциясының анықталу облысы ;
функциясының анықталу облысы ;
б) егер
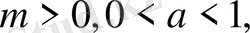 онда шешімі
онда шешімі
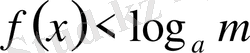 болады ;
болады ;
в) егер
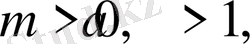 онда шешімі
онда шешімі
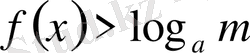 болады;
болады;
3.
 түрінде берілсе:
түрінде берілсе:
а) егер
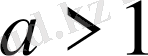 , онда шешімі
, онда шешімі
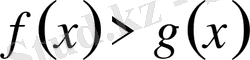 болады;
болады;
б) егер
 , онда шешімі
, онда шешімі
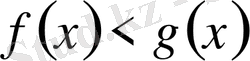 болады.
болады.
Логарифмдік теңсіздіктер:
1.
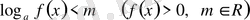 болса:
болса:
а) егер
 болса, онда шешім
болса, онда шешім
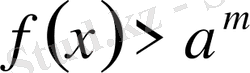 болады;
болады;
б) егер
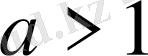 болса, онда шешім
болса, онда шешім
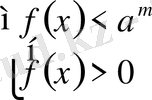 болады.
болады.
2.
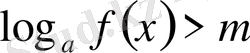 түрінде берілсе:
түрінде берілсе:
а) егер
 болса, онда шешім
болса, онда шешім
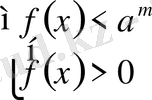 болады;
болады;
б) егер
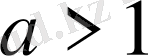 болса, онда шешім
болса, онда шешім
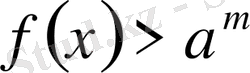 болады.
болады.
3.
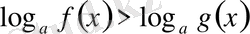 түрінде берілсе:
түрінде берілсе:
а) егер
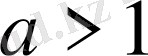 , онда шешім
, онда шешім
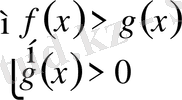 болады;
болады;
б) егер
 , онда шешім
, онда шешім
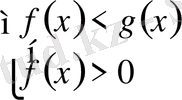 болады.
болады.
Теңсіздіктерге байланысты есептер шығару
Мысал 1.
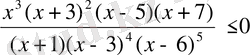 теңсіздігін шешейік.
теңсіздігін шешейік.
1) Берілген өрнектің барлық нөлдері мен үзіліс нүктелерін сандық осьте белгілейік.
2)
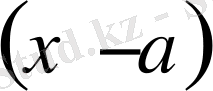 дәрежесі жұп болатын нүктелерді белгілейік.
дәрежесі жұп болатын нүктелерді белгілейік.

3) Таңба аралықтарын белгілеп функцияның таңбасын анықтаймыз.
Жауабы:
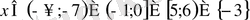 .
.
Мысал 2.
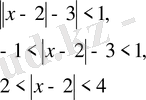
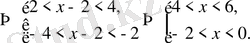
Жауабы:

Мысал 3.
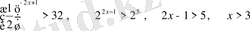
Жауабы:
 немесе
немесе
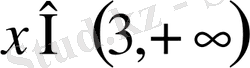
Мысал 4.
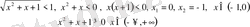
Жауабы:
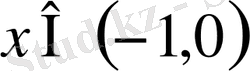
Мысал 5.
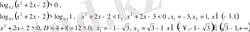
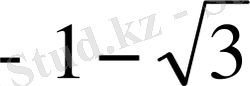
Жауабы:
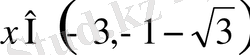
Мысал 6. sinx≥
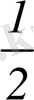
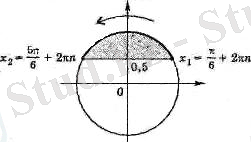 Шешуі: Теңсіздік бірлік шеңбердің барлық нүктелерін қанағаттандырады және ординатасы
Шешуі: Теңсіздік бірлік шеңбердің барлық нүктелерін қанағаттандырады және ординатасы
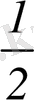 -ден үлкен немесе тең. Бұл нүктелер жиыны төмендегі суретте доға түрімен бейнеленген. Шектелген, штрихталған сегмент. Доғаның шекарасын анықтап, теңдеуді шешеміз
-ден үлкен немесе тең. Бұл нүктелер жиыны төмендегі суретте доға түрімен бейнеленген. Шектелген, штрихталған сегмент. Доғаның шекарасын анықтап, теңдеуді шешеміз
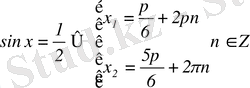
Шеңбер бойымен оң бағытта қозғалғанда қозғалыс сағат тіліне қарсы болады. Яғни біз х
1
=
 +2
+2
 n нүктесімен х
2
=
n нүктесімен х
2
=
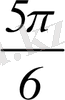 +2
+2
 n нүктесіне бөлік доға бойымен жүреміз, бұдан х
1
<х
2
Сондықтан мынандай жауап аламыз:
n нүктесіне бөлік доға бойымен жүреміз, бұдан х
1
<х
2
Сондықтан мынандай жауап аламыз:
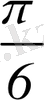 +2
+2
 n≤х≤
n≤х≤
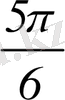 +2
+2
 n, n
n, n
 Z.
Z.
Жауабы: [
 +2
+2
 n;
n;
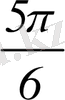 +2
+2
 n], n
n], n
 Z.
Z.
Есептер интерактивті тақтадағы ұяшықтар арқылы таңдалады.
1.
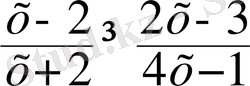 6.
6.
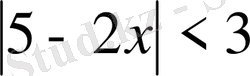
2.
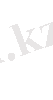
7.
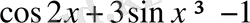
3.
8.
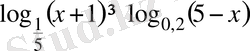
4.
9.
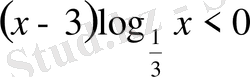
- 10.
Кестені толтырыңдар:
Қос теңсіздік
Бағалау
керек
Өткен сабакты еске түсіру үшін мына тактаға караймыз.
Сандарды салыстыру, санды теңсіздіктердің қасиеттерін тұжырымда.
І кезең
Қандай теңдеуді бір айнымалысы бар сызықтық теңдеу деп атайды?
ах=b түріндегі теңдеуді бір айнымалысы бар сызықтық теңдеу деп атайды.
Мұндағы: х - айнымалы а және b - қандай да бір сандар
2. Қандай теңдеулер мәндес теңдеулер деп аталады?
Түбірлері бірдей теңдеулерді мәндес теңдеулер деп атайды.
«Білу
Тапсырмалары Кім? Не? Қалай? Қашан? Қандай?»
ІІ кезең
Бос орынға қажетті сөзді жаз
- a мен b сандарын салыстырғанда, а - b айырмасы оң сан болса, онда а>b болады.
Мысалы: а= 7, b= 2 болса, а - b ≥ 0 болады.
- > немесе < белгілері қарама-қарсы теісіздік белгілері деп, ал > және > немесе < және < белгілері бірдей теңсіздік белгілері деп аталады.
Мысалы, 6 > 0 және 2<4 - қарама-қарсы теңсіздік белгілері бар санды теңсіздіктер, ал 7> 5 және 9 >2 - бірдей теңсіздік белгілері бар санды теңсіздіктер.
Бос орынға қажет сөзді жаз:
- а және b сандарының қайсысы үлкен, қайсысы кіші екенін \қалай білеміз?
Егер а - b айырмасы оң сан болса, онда а > b болады.
Егер а - b айырмасы теріс болса, онда а < b болады.
- Координаталық түзуде үлкен сан кіші санның қай жағында кескінделеді?
Координаталық түзуде үлкен сан кіші санның оң жағында кескінделеді.
Айырмашылықты тап:
Қатаң теңсіздіктер мен қатаң емес теңсіздіктердің айырмашылығы неде?
Қатаң теңсіздіктер < және > белгілерімен, ал қатаң емес теңсіздіктер ≤ және ≥ белгілерімен беріледі.
Блок - схеманы толтыр:
ІІІ.


2) Үй жұмысы тақтада №133
а) Бегайдаров. (х-2) (х-5) (х-12) > 0

Ж/бы: (2; 5) U(12; +∞)
б) Бисингалиев (х+7) (х+1) (х-4) < 0

Ж/бы: (-∞; -7) U(-1; 4)
в) Кармысов х(х+1) (х+5) (х-8) > 0

Ж/бы: (-∞; -5) U(-1; 0) U(8; +∞)
3) Қазір топпен есеп шығаруға көшеміз. Бүгін 4 топ жұмыс атқарады. Әрбір топ 5 есептен тұратын карточка алады. Әр топтан 1 оқушыдан тақтаға шығып (есепті шығарып болуына қарай) кезек-кезек тапсырмаларды орындау керек. 3-4 есеп мұқияттылықты қажет етеді. Соңғы тапсырмаға топ жетекшісінің өзі шығады.
4) Гүлжан тобы: Бегайдарова 5
- (х+9) (х+1) (х-11) >0 Наришев 3
 Төлемісова 4
Төлемісова 4
Бисингалиев 5
Кенжебекова 4
Ж/бы: (-9; -1) U(11; +∞)
 2) (х
2
-1) (х+5) ≥ 0
2) (х
2
-1) (х+5) ≥ 0
-1; 1 -5
Ж/бы: [-5; -1] U[1; +∞)
3. (4-х 2 ) (10х+35) <0 7х
(х-2) (х+2) (х+3, 5) >0 4. 4х-10 ≤ 0
 2 -2 -3, 5 7(х) (4х-10) ≤0
2 -2 -3, 5 7(х) (4х-10) ≤0
х(х-2, 5) ≤0

Ж/бы: (-3, 5; -2) U(2; +∞)
Ж/бы: [0; 2, 5)
5. х+3
х 2 +4х-5 ≥ 0
 (х+3) (х+5) (х-1) ≥0
(х+3) (х+5) (х-1) ≥0
Ж/бы: [-5; -3) U(1; + ∞)
Гүлдәурен тобы:
 1. х(х+9) (х-13) ≤0 Бекмуханбетова 5
1. х(х+9) (х-13) ≤0 Бекмуханбетова 5
Төлегенова 4
Лұқпанов 3
Ж/бы: (-∞; -9] [0; 13] Бегайдаров 4
Оспанова
3. -(х-1) (х-5) (х+20) >0 2. (2х-1) (х+9) <0
 (х-1) (х-5) (х+20) >0 (х-0, 5) (х+9) <0
(х-1) (х-5) (х+20) >0 (х-0, 5) (х+9) <0

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz