Арифметикалық және геометриялық прогрессиялар мен логарифмдер: теория, формулалар және есептер


Мазмұны
Кіріспе
- Тірек сызба
- Логарифм анықтамасы
- Логарифмдік өрнектерді есептеу әдістері
Қорытынды
Пайдаланған әдебиеттер
Кіріспе
Логарифмді ойлап тапқан және логарифмдік кесте құрастырған ғалым туралы қысқаша айта кетейік. Джон Непер - шотландияда туған. 16 жасында континентке кетіп, 5 жыл Европаның әртүрлі университеттерінде оқып, математиканы игерген. Кейін астрономия және математикамен терең айналысқан. Логарифмдік есептеулер идеясына Непер 16-ғасырдың 80-жылдарында келген, дегенмен өзінің кестесін 25 жыл есептеулерден кейін 1614 жылы ғана жариялаған. Ол «Логарифмдік керемет кестелер сипаты» деген атпен шыққан. «Логарифм» деген терминнің өзін де Непер ұсынған, ол оны «қолдан жасалған сан» деп аударған. Непердің кестелері мен идеялары тез таралып, қолданықа түскен. «Непер ережесін» және «Непер аналогияларын» сфералық тригонометрияда кездестіруге болады.
Тірек сызба

1. Анықтамасы
2. Тану
Арифметикалық прогрессия Геометриялық прогрессия
2. 1. а 1 , а 2 , а 3 , . . . , а n
Мысалы
1, 4, 7, . . .
а 2 - а 1 = а 3 - а 2 = …= a n-1 - a n =d
2. 2. (a n ) - арифметикалық
прогрессия
а 1 - бірінші мүше
d - айырымы
n - мүшелерінің саны
а n - n-ші мүшесі
S n - алғашқы n мүшесінің
қосындысы
b 1 , b 2 , b 3 , . . . , b n
Мысалы
2, 4, 8, 16 . . .
b 2 : b 1 = b 3 : b 2 = …= b n+1 : b n =q
(b n ) - геометриялық
прогрессия
b 1 - бірінші мүше
q - еселік
n - мүшелерінің саны
b n - n-ші мүшесі
S n - алғашқы n мүшесінің
қосындысы
2. 3. Арифметикалық және геометриялық прогрессиялар -
тізбектер. Тізбектер бірнеше тәсілдермен берілетінін еске түсіре кетейік:
2. 4. Математикалық белгі
Арифметикалық Геометриялық
прогрессия прогрессия
3. Қасиеті

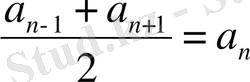
Мысалы
1, 3, 5, 7, . . .
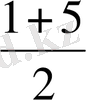
= 3;
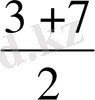
= 5
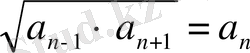
Мысалы
2, 2 2 , 2 3 , 2 4 , . . .
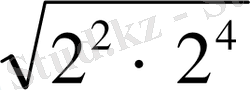
= 2 2
= 2 3
4. Маңызды түйін
4. 1. Рекурренттік формуласы
a
n+1
= a
n
+ d, n
 N b
n+1
= b
n
N b
n+1
= b
n
 q, n
q, n
 N
N
4. 2. Қабылдай алатын мәндері
a
1
 d -
d -
 сандар b
1
сандар b
1
 0, q
0, q
 0
0
d - айырымы q - еселігі
4. 3. Жалпы мүшесінің формуласы
a
n
= a
1
+ (n-1) d b
n
= b
1
 q
n-1
q
n-1
Айырымын табу: Еселікті табу:
d = a
n+1
- a
n
q =
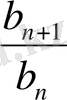 Equation. 3
Equation. 3
4. 4. Алғашқы n мүшесінің қосындысының формуласы
S
n
=
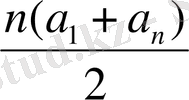 Equation. 3 S
n
=
Equation. 3 S
n
=
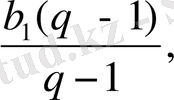 Equation. 3 (q
Equation. 3 (q
 Equation. 3 1)
Equation. 3 1)
4. 5. Шексіз кемімелі
геометриялық
прогрессияның
қосындысы
S =
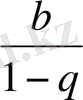 Equation. 3 ;
Equation. 3 ;
 < 1
< 1
5. Түрге айыру
5. 1. Арифметикалық прогрессия
d>0, өспелі
айырымы арифметикалық прогрессия
d<0, кемімелі
5. 2. Мүшелері тұрақты бір ғана сан болатын тізбек тұрақты
геометриялық прогрессия деп аталады.
Мысалы: 4, 4, 4, . . . тізбегі q = 1 болғанда тұрақты
геометриялық прогрессия болады.
6. Түрлену
Арифметикалық прогрессия Геометриялық прогрессия
6. 1.
Equation. 3 мүшесін табу
a 1 = 2 b 1 = 3
d = 5 q = 2
a 7 - ? b 5 - ?
а
7
=a
1
+6d=2+30=32 b
5
=b
1
 q
4
=3
q
4
=3
 2
4
=3
2
4
=3
 16=48
16=48
6. 2. Айырымын табу 6. 3. Еселігін табу
a 1 =5 b 1 = 3
a 2 =7 b 2 = 9
d - ? q - ?
a
2
= a
1
+ d b
2
= b
1
 q
q
d = a
2
-a
1
q =
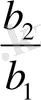 =
=
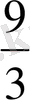 = 3
= 3
d = 2 q = 3
6. 4.
мүшелерінің қосындысын есептеу
a 1 = 9 b 1 = 1
a
2
= 13 q =
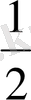
S 5 - ? S 4 - ?
d = a
2
- a
1
= 13 - 9 = 4 b
4
= b
1
 q
3
= 1
q
3
= 1
 (
(
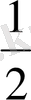 )
3
=
)
3
=

a 5 = a 1 +4d = 9+16=25
S
5
=
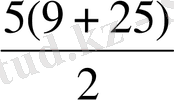 =
=
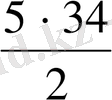 = 85 S
4
=
= 85 S
4
=
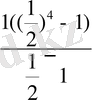 =
=
 = =
= =
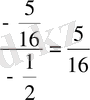
 2 =
2 =
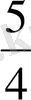 =1
=1
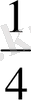
3. Есептер шығару
№1. Арифметикалық прогрессияның бірінші мүшесі 5-ке тең, айырымы
7-ге тең, оның он екінші мүшесі неге тең екенін бізден сұрайды.
Берілгені: а 1 =5
d=7
a 12 =?
Шешуі:
a
12
= a
1
+ 11d=5+11
 Equation. 3 7=82
Equation. 3 7=82
Жауабы: 82
№3. Арифметикалық прогрессияның бірінші мүшесі 25-ке, айырымы 4-ке тең, оның алғашқы он мүщесінің осындысын табыңдар.
Берілгені: a 1 = 25
d=4
S 10 - ?
Шешуі:
a
10
= a
1
+ 9d=25+9
 4=61
4=61
S
10
=
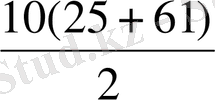 = 5
= 5
 86 = 430
86 = 430
Жауабы: 430
№5. Берілгені: a 10 = 120
d = 12
a 1 - ?
Шешуі:
a 10 = a 1 + 9d
a 1 =a 10 -9d=120-108=12
a 1 =12
Жауабы: 12
№2.
Геометриялық прогрессияның бірінші мүшесі 3-ке, еселігі
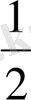 - ге тең, оның үшінші мүшесі неге тең екені бізден сұрайды.
- ге тең, оның үшінші мүшесі неге тең екені бізден сұрайды.
Берілгені: b 1 =3
q=
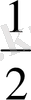
b 3 =?
Шешуі:
b
3
= b
1
 Equation. 3 q
2
=3
Equation. 3 q
2
=3
 Equation. 3
Equation. 3
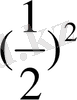 Equation. 3 = 3
Equation. 3 = 3
 Equation. 3
Equation. 3
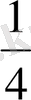 Equation. 3 =
Equation. 3 =
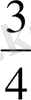 Equation. 3
Equation. 3
Жауабы:
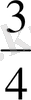 Equation. 3
Equation. 3
№4. Геометриялық прогрессияның бірінші мүшесі мен үшінші мүшесінің қосындысы 60-қа тең, еселігі 3-ке тең. Оның алғашқы төрт мүшесінің қосындысын табыңдар.
Берілгені: b 1 +b 3 = 60
q = 3
S 4 - ?
Шешуі:
b
3
= b
1
 q
2
q
2
b 1 + b 1 q 2 = 60
b 1 (1+q 2 ) = 60
b 1 (1+9) = 60
10b 1 =60
b 1 =6
S
4
=
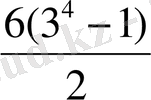 = 3
= 3
 80 = 240
80 = 240
Жауабы: 240
№6. Берілгені: b 1 =5
b 5 =3125
q - ?
Шешуі:
b 5 =b 1 q 4 ;
q
4
=
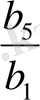 Equation. 3 =
Equation. 3 =
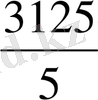 Equation. 3 =625
Equation. 3 =625
q 4 = 625
q 4 = 5 4
q = 5
Жауабы: q = 5
4. Деңгейлік тапсырмалар бойынша тест алу
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz