Кіші кешенді мектептерде математиканы оқыту әдістемесі: квадрат теңдеулерді шешу жолдары және компьютерлік есептеу технологиялары арқылы математикалық біліктілікті дамыту


МАЗМҰНЫ
КІРІСПЕ
I. КІШІ КЕШЕНДІ МЕКТЕПТЕРДЕ МАТЕМАТИКАНЫ ОҚЫТУ ӘДІСТЕМЕСІ
II. КОМПЬЮТЕРДЕ ЕСЕП ШЫҒАРУ ТЕХНОЛОГИЯСЫН МАТЕМАТИКАЛЫҚ БІЛІКТІЛІКТІ ТЕРЕҢДЕТУДЕ ЖӘНЕ ДАМЫТУДА ПАЙДАЛАНУ
III. КВАДРАТ ТЕҢДЕУЛЕРДІ ШЕШУ ЖОЛДАРЫНЫҢ ӘР ТҮРЛІ ӘДІСТЕРІ
ҚОРЫТЫНДЫ
КІРІСПЕ
Мектептерде математика пәнін оқытудың алдында жалпы мақсаттармен қатар осы ғылымның ерекшеліктеріне сүйенетін спецификалық мақсаттар да тұр. Олардың бірі - математикалық ойлауды қалыптастыру және дамыту. Бұл оқушылардың математикалық жетістіктерінің пайда болуына және нәтижелі дамуына себеп болады.
Баланың интелектуалдық ойлау қабілетін үш бағытта жылдамдатуға болады: ойлаудың түсінікті құрылуы, сөйлеу интелектісі және жоспар құру.
Жақсы білімді қалыптастыру белгілі бір мақсатқа бағытталған ойлаусыз жүзеге аспайды, сондықтан ол қазіргі уақытта мектептегі оқытудың негізгі мақсаттарының бірі болып табылады.
Балалардың қарапайым есептеуді үйренуі жайлы алғашқы ақпараттар Ежелгі Шығыс елдерінің тарихи жазбаларында кездеседі. Мектептегі математикалық білім берудің дамуына Ежелгі Грециядағы математикалық мәдениет үлкен септігін тигізді, мұнда б. э. д. 5 ғасырда сауданың және теңізде жүзудің дамуына байланысты бастауыш мектептерде есеп және практикалық геометрия оқытылды.
Уақыт өте келе білім берудің мақсаттарының көбеюіне, мектептегі дайындауда жаңа шарттардың пайда болуына, білім беру стандартының өзгеруіне байланысты бұл оқу пәнінің мазмұны өзгеруде.
Сонымен қатар, ғылымның үздіксіз дамуы, оның жаңа бөлімдері мен бағыттарының пайда болуы математика пәнінің мазмұнының өзгеруін талап етеді: тәжірибелік құндылығы жоқ бөлімдер қысқартылады, жаңа актуальді және перспективті тақырыптар кірістірілуде. Осы айтылғандардың барлығымен қатар педогогикалық білім де өз орнында тұрған жоқ.
Кіші кешенді мектептерде математиканы оқыту әдістемесі
Математиканың оқу курсы үнемі математика - дамушы ғылым мен математика - оқу пәні арасындағы келіспеушіліктерді жеңіп отыруы тиіс. Ғылымның дамуы математикалық білім берудің мазмұнының үздіксіз жаңаруын, оқу пәнінің ғылыммен ұштастырылуын, мазмұнының қоғамдағы әлеуметтік қажеттіліктерге сай болуын талап етеді. Математиканы оқытудың әдістемесі - бұл математиканы оқытудағы тапсырмалар, мазмұн және әдістер жайлы педогогикалық ғылым. Ол пәннің нәтижелігі мен құндылығын арттыру мақсақсатында математикалық білім беру процесін оқытады және зерттейді. Математиканы оқытудың әдістемесі математиканы қалай беру керек жайлы сұрақты қарастырады.
Математитканы оқыту әдістемесінің мақсаты мектептегі математиканы оқыту жүйесінің негізгі компоненттері мен олардың арасындағы байланысты зерттеу болып табылады. Мұның негізгі компоненттері деп математиканы оқытудың мақсатын, мазмұнын, әдістерін, формалары мен құралдарын түсіну керек.
Математитканы оқыту әдістемесінің пәні өзінің қиындығымен ерекшеленеді. Математитканы оқыту әдістемесінің пәні математикалық білім беру болып табылады. Ол математиканы игерудегі мақсаттар мен мазмұннан, әдістерден, құралдардан және формалардан тұрады.
Математиканы оқыту әдістемесі қазіргі кезде үлкен қиыншылықтарды бастан өткізуде. Бұл ең алдымен мектеп қабырғасындағы математика мен математикалық ғылымды бір-бірімен біріктіру қиынға түскендіктен, сонымен қатар ол философия, математика, логика, психология, биология, кибернетика және өнермен байланыста болатын педогогиканың шекарасы болғандықтан.
Математиканы оқыту әдістемесінің негізгі қызметтері:
- Сынып бойынша, сабақ тақырыбы бойынша математиканы оқытудың нақты мақсаттарын анықтау;
- Оқу құралының мазмұны мақсаттарға және оқушылардың танымдық қабілеттеріне сәйкес келуін қадағалау;
- Қойылған мақсаттардың жүзеге асуына бағытталған сабақ берудегі жаңа ұтымды әдістер мен ұйымдастырушылық формаларды құру;
- Оқытуға қажетті құралдарды қарастыру және мұғалімнің жұмыс тәжірибесінде оларды қолдануға арналған көрсеткіштер шығару.
Математиканы оқыту әдістемесінің көмегімен келесі үш сұраққа жауап алуға болады: Математиканы не үшін оқу керек? Нені оқу керек? Математиканы қалай оқыту керек?
Бағдарламада қарастырылған мектептегі математиканың мазмұны ондағы болып жатқан өзгерістерге қарамастан ұзақ уақыт бойы өзінің негізгі мағынасын жоғалтқан жоқ. Бағдарламаның негізгі мазмұнының мұндай тұрақтылығы мынамен түсіндіріледі: математика өзінің дамуында көптеген жаңалықтарды аша отырып, оның алдында жиналған білімдерді де ескірген және керексіз деп тастамай, сақтап отырады. Бұл бөлімдерге кіргендердің әрбіреуінде орта мектепте оқытылатын пән ретінде өздерінің даму тарихы бар. Оларды оқыту жайлы сұрақтар арнайы математикадан сабақ беру әдістемесінде көрсетілген.
Оқыту әдісі - дидактикалық құралдар мен тәсілдердің кешені, олардың көмегімен оқыту мен тәрбие берудің мақсаттары жүзеге асады. Оқыту әдісі - бұл мұғалім мен оқушылардың мақсатқа бағытталған әрекеттерінің байланысқан түрі. Оқыту әдісі деп мұғалім мен оқушылардың белгілі бір дидактикалық мақсатты жүзеге асыруға арналған кезектесіп отыратын әрекет ету тәсілдерін айтады.
Сабақ беру әдісі - оқушылардың танымдық қабілеттерін басқаруға және бақылауға арналған құралдар мен тәсілдер, ақпарат алмасу жолдары.
Оқу әдісі - оқу материалын қабылдаудың жолдары, құралдары мен тәсілдер, оқу мен өзін-өзі бақылаудың репродуктивті және продуктивті әдістері.
Математикалық зерттеудің басты әдістеріне жатады: бақылау және тәжірибе, анализ және синтез, салыстыру, жалпылау және специализация, абстрактілеу және конкретизация.
Математиканы оқытуда қолданылатын қазіргі замандағы әдістер: проблемалы (перспективті) әдіс; зертханалық әдіс; бағдарламаланған оқыту әдісі; эвристикалық әдіс; математикалық модельдерді құру әдісі; аксиоматикалық әдіс және т. б.
Оқытудың ақпараттық дамушы әдістері екі класқа жіктеледі:
- Ақпаратты дайын түрінде беру (дәріс, түсіндіру, оқуға арналған кинофильмдер мен видеофильмдерді демонстрациялау және т. б. ) ;
- білімді өз бетінше табу (оқулықпен өз бетінше жұмыс, оқу бағдарламасымен өз бетінше жұмыс, берілгендердің ақпараттық базасымен жұмыс - ақпараттық технологияларды қолдану) .
Проблемалық-іздеуші әдістерге мыналар жатады: Оқу материалын проблемалы талқылау (эвристикалық әңгімелесу), оқу дискуссиясы, зертханалық іздеуші жұмыс, кіші топтармен жұмыс істеген кезде ұжымдық ойлау қабілеттерін (ҰОҚ) ұйымдастыру, зерттеуші жұмыс, ұйымдастырушылық-әрекет етуші ойын.
Репродуктивті әдістер: оқу материалын мазмұндау, мысал бойынша жаттығуларды орындау, инструкция бойынша зертханалық жұмыс.
Мәдени-репродуктивті әдістер: шығарма, вариациялық жаттығулар, өндірістік жағдайларды анализдеу, әртүрлі ойындарды ұйымдастыру және мамандандырылған әрекеттерді имитациялаудың басқа түрлері.
Мұғалім мен оқушылардың әрекеттерінің тәсілдері оқыту әдістерінің құраушы бөлігі болып табылады (М. И. Махмутов) . Тәсілдер - белгілі бір тапсырманы орындауға бағытталған әрекеттер, қызмет ету түрлері. Оқу жұмысының тәсілдері ойлау әрекетінің тәсілдеріне тәуелді (анализ және синтез, салыстыру және жалпылау, дәлелдеу, абстрактілеу, конкретизация, қорытынды шығару, көз алдына елестету және еске сақтау тәсілдері) .
Оқытудың арнайы әдістері - математиканың өзінде қолданылатын оқуға адаптацияланған танымның негізгі әдістері, нақтыны оқуда математикаға тән әдістер (математикалық модельдерді құру, осындай модельдерді құруда қолданылатын абстрагтілеу тәсілдері, аксиоматикалық әдіс) .
Мұның нәтижесінде математика курсына бірнеше әдістемелік көрсеткіштерді ұсынуға болады:
Математиканы оқытуды жақсарту мақсатында стандартты емес есептерді пайдалануға арналған жаңа әдістерді ары қарай шығарған жөн.
Сабақта үнемі оқушылардың өз бетімен жұмыс жасау қабілеттері мен танымдық қызығушылықтарының қалыптасуына көмектесетін тапсырмаларды пайдалану керек.
Арнайы таңдап алынған жаттығулардың көмегімен оқушыларды берілген тапсырмаларды орындауға үйрету, оларды бақылауға үйрету, аналогияны, индукцияны, салыстыруды қолдану және қорытынды шығару.
Сабақ кезінде жылдам ойлануға арналған тапсырмаларды, математикалық ребустарды, софизмдерді, күлкілі есептерді пайдаланған дұрыс.
Оқушылардың индивидуалді қасиеттерін есте ұстау, әртүрлі типті тапсырмаларды қолданып олардың әрбіреуіндегі танымдық әрекеттерді дифференциялау.
Оқыту процесі кезінде мұғалімнің оқушылардың танымдық қызығушылықтарын қоздыруы, жақсартуы және дамытуы оның өз пәнінің мазмұнын бай, терең, қызықты етіп және оқушылардың танымдық әрекеттерінің тәсілдерін әртүрлі, шығармашылық, продуктивті етіп жасай білуінде.
КВАДРАТ ТЕҢДЕУЛЕРДІ ШЕШУ ЖОЛДАРЫНЫҢ ӘР ТҮРЛІ ӘДІСТЕРІ
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.
Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Бұл жұмыс алгебра курсында қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.
«Квадрат теңдеулер» мектептегі алгебра курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с. с. мазмұнды есептердің шығарылуы квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т. б. жағдайларда квадрат теңдеулерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.
Зерттеу барысында мектеп оқушыларына «квадрат теңдеулерді» шешу жолдарының тоғыз түрлі әдісімен таныстыруға мүмкіндік бар екендігін анықтадық. Атап айтқанда, олар төмендегідей болып табылады:
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу
Мысал: х 2 +4х+3 =0 теңдеуін шешейік.
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х 2 +х+3х+3 =х(х+1) +3 (х+1) =(х+1) (х+3)
Демек, теңдеуді былай жазуға болады: (х+1) (х+3) =0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х
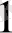 =-1 және
=-1 және
 сандары х
2
+4х+3=0 теңдеуінің түбірлері болып табылады.
сандары х
2
+4х+3=0 теңдеуінің түбірлері болып табылады.
2-әдіс. Толық квадратқа келтіру әдісі
Мысал: х 2 +8х-9=0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х 2 +8х өрнегін төмендегідей жазып аламыз: х 2 + 8х=х 2 +2х4
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 4-тің екі еселенгені. Толық квадрат алу үшін 4 2 -ын қосу керек. Сонда х 2 +2х4+4 2 =(х+4) 2
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 4
2
-ын қосып, алып тастаймыз. Сонда шығатыны: х
2
+8х-9=х
2
+2х4+4
2
-9-4
 =(х+4)
2
-25
=(х+4)
2
-25
Сонымен, берілген теңдеуді былайша жазуға болады: (х+4) 2 -25=0, яғни (х+4) 2 =25.
Бұдан х+4=5, х
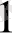 =1 немесе х+4=-5, х
=1 немесе х+4=-5, х
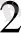 = -9. Жауабы: 1; -9
= -9. Жауабы: 1; -9
3-әдіс. Квадраттық теңдеулерді формула арқылы шешу
ах 2 +вх+с=0, а≠0 теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:
4а 2 х 2 +4ахв+4ас=0
((2ах) 2 +4ахв+в 2 ) -в 2 +4ас=0, (2ах+в) 2 =в 2 -4ас
2ах+в=
Equation. 3
, 2ах = -в
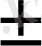
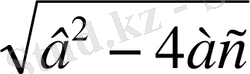
х
=
(1)
Оған келесідегідей мысалдар келтіруге болады:
1) 3 х 2 - 7 х+ 4=0 теңдеуін шешейік.
а=3, в=-7, с=4. Д=в 2 -4ас=(-7) 2 -4·4·3=49-48=1.
Д>0 болғандықтан, екі әр түрлі түбір болады: х
1
=1, х
2
=
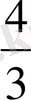
Сонымен, дискриминант оң болғанда, яғни в 2 -4ас>0, ах 2 +вх+с=0 теңдеуінің екі түрлі түбірі болады.
2) 9х 2 +6х+1=0 теңдеуін шешейік.
а=9, в=6, с=1. Д=в 2 -4ас=6 2 -4·9·1=0.
Д=0 болғандықтан, бір ғана түбір бар болады: х=
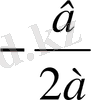 , х=
, х=
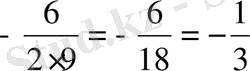
Сонымен, егер дискриминант нөлге тең болса, яғни в 2 -4ас=0, ах 2 +вх+с=0 теңдеуінің жалғыз
түбірі бар болады: х=
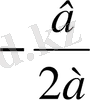
3) х 2 +2х+3=0 теңдеуін шешейік.
а=1, в=2, с=3. Д=в 2 -4ас=4-4·3·1= -8.
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды.
Сонымен, егер дискриминант теріс болса, яғни в 2 -4ас<0, онда ах 2 +вх+с=0 теңдеуінің түбірі болмайды.
4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу
Келтірілген түбірлері Виет теоремасын қанағаттандырады.
Ол былай беріледі: а=1 болғанда,
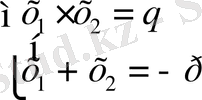
Бұдан келесі тұжырымдарды шығаруға болады:
а) Егер q (1) теңдеудің бос мүшесі оң болса (q
 0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.
0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.
Мысал, 1) х 2 -9х+20=0, х 1 =4, х 2 =5, мұнда q=20 >0, р=-9 <0;
2) х 2 +5х+6 =0, х 1 =-2, х 2 =-3, мұнда q =6 >0, р =5 >0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0. Мысал, 1) х 2 +3х-4 =0; х 1 =-4, х 2 =1 мұнда q =-4 <0, р=-3 >0
2) х 2 -7х-8 =0; х 1 =8, х 2 =-1 мұнда q =-8 <0, р =-7 <0
5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу
ах
2
+вх+с =0, а ≠0 квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз: а
2
х
2
+авх+ас=0. ах =у деп белгілесек, х =
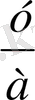 . Олай болса у
2
+ву+ас =0 теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у
1
, у
2
-ні Виет теоремасы арқылы табамыз. Соңында х
1
=
. Олай болса у
2
+ву+ас =0 теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у
1
, у
2
-ні Виет теоремасы арқылы табамыз. Соңында х
1
=
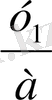 , х
2
=
, х
2
=
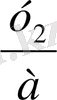 -ны аламыз. Бұл жағдайда
-ны аламыз. Бұл жағдайда
а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды [1, 13бет] . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
Мысал: 2х 2 -9х+9=0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде
у 2 -9у+18=0 теңдеуін аламыз. Виет теоремасы бойынша
Жауабы: 3; 1, 5.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану
ах 2 +вх+с=0, а≠0 квадрат теңдеуі берілген.
Егер а+в+с=0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х
1
=1, х
2
=

Мысал: 7+2-9=0 қосындысы 0-ге тең. Осы үш сан үшін квадрат теңдеу құрастырып, оны шешейік:
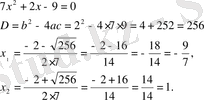
7-әдіс. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу
ах
2
+вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен шешу әдісін ұсынамыз (1-сурет) . Ізделінді шеңбер абцисса өсінде В(х
 ; 0) және Д (х
2
; 0) нүктелерінде қиылыссын делік. Мұндағы х
1
, х
2
- ах
2
+ вх + с=0 теңдеуінің түбірлері және ординат осінен А(0; 1) және С(0;
; 0) және Д (х
2
; 0) нүктелерінде қиылыссын делік. Мұндағы х
1
, х
2
- ах
2
+ вх + с=0 теңдеуінің түбірлері және ординат осінен А(0; 1) және С(0;
 ) нүктелері арқылы өтеді делік. Олай болса, қима туралы теорема бойынша мынаны аламы
) нүктелері арқылы өтеді делік. Олай болса, қима туралы теорема бойынша мынаны аламы
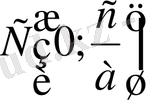
ОВ·ОД=ОА·ОС,
бұдан ОС=
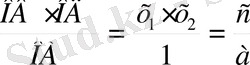
1-сурет
Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен SК-ның
қиылысу нүктелері болып табылады, сондықтан
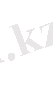 SК=
SК=
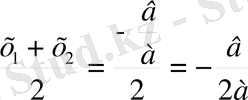 ;
;
SF =
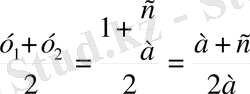
Сонымен,
1) S
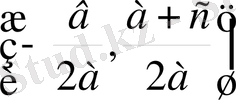 (шеңбер центрі) және А (0; 1) нүктелерін тұрғызамыз;
(шеңбер центрі) және А (0; 1) нүктелерін тұрғызамыз;
2) SА радиусты шеңбер жүргіземіз;
3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат теңдеудің түбірі болады.
Сонымен үш түрлі жағдай болуы мүмкін:
1-ші жағдай. Шеңбер радиусы ордината центрінен артық (АS > SК, немесе,
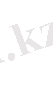
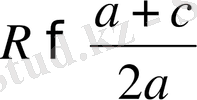 шеңбер Ох осін екі нүктеде (2а-сурет) В (х
шеңбер Ох осін екі нүктеде (2а-сурет) В (х
 ; 0) және Д (х
2
; 0) нүктелерде қияды. Мұндағы х
1
және х
2
-ах
2
+вх+с =0 квадрат теңдеуінің түбірлері) .
; 0) және Д (х
2
; 0) нүктелерде қияды. Мұндағы х
1
және х
2
-ах
2
+вх+с =0 квадрат теңдеуінің түбірлері) .
2-ші жағдай. Шеңбер радиусы ордината центрінде (АS= SК; немесе
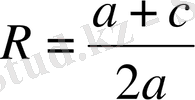 тең, шеңбер Ох осін В (х
1
; 0) нүктесінде (2б) -сурет) жанап өтеді, мұндағы х
1
- квадрат теңдеудің түбірі) .
тең, шеңбер Ох осін В (х
1
; 0) нүктесінде (2б) -сурет) жанап өтеді, мұндағы х
1
- квадрат теңдеудің түбірі) .
3-ші жағдай. Шеңбер радиусы ордината центрінен кіші (А S < SК, немесе
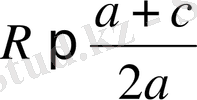 ) кем, щеңбердің абцисса осімен қиылысатын нүктесі жоқ (2в - сурет), бұл жағдайда теңдеудің шешімі болмайды.
) кем, щеңбердің абцисса осімен қиылысатын нүктесі жоқ (2в - сурет), бұл жағдайда теңдеудің шешімі болмайды.
у у у
2-сурет
а) АS>SВ,
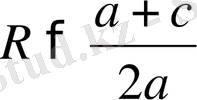 екі шешімі бар: х
1
және х
2
екі шешімі бар: х
1
және х
2
б) АS=SВ,
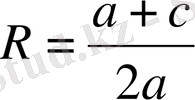 бір шешімі бар: х
1
бір шешімі бар: х
1
в) АS<SВ,
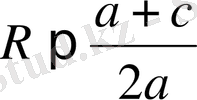 шешім жоқ.
шешім жоқ.
8-әдіс. Квадрат теңдеуді номограмма көмегімен шешу
O B E y 3
F D
y y
 3y
3y
H A
C
3 3y 9
p q 3-сурет 4- сурет
Бұл квадрат теңдеуді шешудің бұрынғы және жөнсіз ұмыт болған әдісі [2, 83бет] .
Брадис таблицасында z 2 +pz+q=0 теңдеуін шешуге арналған номограмманы қарастырайық. Бұл номограмма квадрат теңдеудідің түбірлерін анықтауға мүмкіндік береді. Номограмманың қисық сызықты шкаласы төменгі формулалар бойынша тұрғызылған (жоғарыдағы 3-суретте бейнеленген) .
ОВ=
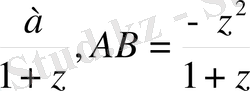 ОС=р, ЕД=q, ОЕ=а десек, мұндағы САН және СДF үшбұрыштарының ұқсастығына мынадай пропорция аламыз:
ОС=р, ЕД=q, ОЕ=а десек, мұндағы САН және СДF үшбұрыштарының ұқсастығына мынадай пропорция аламыз:
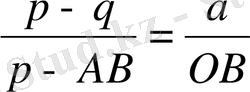 Мұнда z
2
+pz+q=0 теңдеуді ауыстыру жасағаннан және жеңілдеткеннен шығады, бұл жердегі z әрпі қисық сызықты шкала нүктесінің кез-келген белгісін білдіреді.
Мұнда z
2
+pz+q=0 теңдеуді ауыстыру жасағаннан және жеңілдеткеннен шығады, бұл жердегі z әрпі қисық сызықты шкала нүктесінің кез-келген белгісін білдіреді.
9-әдіс. Квадрат теңдеулерді геометриялық әдіспен шешу
Көне заманда алгебраға қарағанда геометрия көбірек жетілген кезде, квадрат теңдеулерді алгебралық жолмен емес геометриялық жолмен шеше білген. Ежелгі гректер мына у 2 + 6у-16=0 теңдеуін қалай шешкендігіне тоқталып өтейік.
Шешуі: жоғарыдағы 4-суретте көрсетілген, мұндағы у 2 +6у=16 немесе у 2 +6у+9=16+9
у 2 +6у+9 және 16+9 өрнекті геометриялық тұрғыда сол квадраттың өзін береді, ал
у
2
+6у-16+9-9=0 бастапқы теңдеу де сол теңдеу. Бұдан алатынымыз у+3=
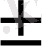 5 немесе у
1
=2, у
2
=-8.
5 немесе у
1
=2, у
2
=-8.
Мақалада қарастырылған 9 әдіс те оқушылардың «Квадрат теңдеулер» тақырыбын терең меңгеруіне жол ашады. Сонымен қоса, квадрат теңдеулерді шешудің барлық тоғыз әдісі де қолданыс тапқанда оқушылардың пәнге деген қызығушылығы мен логикалық ойлау қабілеті артады.
КОМПЬЮТЕРДЕ ЕСЕП ШЫҒАРУ ТЕХНОЛОГИЯСЫН МАТЕМАТИКАЛЫҚ
БІЛІКТІЛІКТІ ТЕРЕҢДЕТУДЕ ЖӘНЕ ДАМЫТУДА ПАЙДАЛАНУ
Практикалық және өмірлік, ғылыми есептерді шешуді компьютер көмегімен есепті шыға руға дайындау және шығару технологиясын пайдалана отырып, тиімді ұйымдастыру ға болатынын практика дәлелдеп отыр. Осы технологияны математика пәнін оқытуда, оқу шылар/студенттер білімін бекітуде, толықтыруда, пәнаралық байланыстарды мазмұнды іске асыруда, тереңдетуде және дамытуда да тиімді пайдалануға болады. Бұл технология ны пайдалану оқушылардың/студенттердің бойында жеке өз бетінше шығармашылық тұрғыда жұмыс істеу, іздену, ойлана білу, талдаушылық, шешім қабылдау, оқулық мате риалды саналы түсінуге тырысу қасиеттерін қалыптастырады. Нәтижесінде оқушының білімі, біліктілігі мазмұнды тереңдейді, танымдық деңгейі кеңейеді және дами түседі.
Мысал карастырайық. Наурыз айының бір декадасындағы ауа температурасы және жауған жауын-шашын мөлшерлері туралы мәлімет берілген. Осы декадада жауын түрінде және қар түрінде түскен күндеріне сәйкес олардың жалпы мөлшерлерін анықтаңыздар.
Мысалы, мұндай есептерді циклдық структуралы және массивтермен жұмыс істеу алгоритмдері туралы тақырыптарды (9-11 сыныптарда, ЖОО-ның 1-2 курстарында) теориялық тұрғыда оқып-үйренгеннен кейін барып немесе осы тақырыптарды қорытындылау барысында ұсынуға болады. Сонда оқушылар теориялық (абстракциялық) тұрғыда білгендерін практикада қолдануға машықтана бастайды. Есепті шешу барысында оқушылар теориялық білімдерін бекітеді, теорияның практикалық қолданысын түсіне бастайды, пәнаралық (мысалы, осы есепте географиямен, метеорологиямен) байланыс мазмұнын көреді, кейбір сирек еститін ұғымдарды естеріне түсіреді, практикалық мәнін түсінеді, олардың танымдық деңгейі кеңейеді және өседі. Есеп мазмұнын талдау барысында өз бетінше шығармашылық тұрғыда ойлана алу, іздену, шешім қабылдау, оқулық материалды саналы түсінуге назар аудару қасиеттері оқушы/студент бойында қалыптасатын болады.
Компьютер көмегімен есепті шығару технологиясының дайындық кезеңдеріне мына мәселелердің кіретіндігі белгілі: есептің қойылуы; есептің моделін құру; есепті шығарудың тиімді әдісін (тәсілін, жолын) таңдау; есепті шығару алгоритмін жазу; есепті шығару программасын жазу.
Біздің қарастырып отырған мысал жағдайында осы кезеңдердің (мәселелердің) мазмұндарына назар аударатын болсақ, мына жағдайларды байқаймыз: бірінші кезеңде есеп мазмұнына талдау жүргізу - өмірмен, математика және география пәндерімен байланысты іске асырады, негізгі қажетті математикалық және географиялық ұғымдар мазмұны еске түсіріледі, қайталанады; екінші кезең - география мен математикалық біліктілікпен байланыстырылады; үшінші кезеңде таза математикалық мәселе қарастырылады; ал төртінші және бесінші кезеңдерде оқушының информатикадан алған білімі, біліктілігі жұмыс істей бастайды. Яғни, осы есепті компьютерде саналы түрде түсініп шығаруы үшін оқушының географиядан, математикадан және информатикадан белгілі бір деңгейдегі білімі және біліктілігі талап етіледі.
Енді, осы кезеңдердің сәйкес мақсаттары және міндеттеріне назар аударайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz