Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3
І. Электромеханикалық ұқсастық жүйелері және электромеханикалық балама ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..6
1.1 Электромеханикалық ұқсастықтың бірінші жүйесі және күш кернеу және екінші жүйесі күш тоқ ... ...6
1.2 Электромеханикалық баламаны қолдану және механикалық жүйе баламаларының.электрлік үлгілерін құру ... ... ... ... ... ... ... ... ... ... ... ... ... 28
1.3 Электромеханикалық жүйелер және осы жүйе тербелістерін зерттеуге Лагранж.Максвелл теңдеулерін қолдану және механикалық жүйе тербелістерін электрлік модельдеу, масштабтық коэффициенттер және ұқсастық индикаторы ... ... ... ... ... ... ... ...30
ІІ. Консервативті күш өрісіндегі жүйе тепе.теңдігінің орнықтылығы ... .39
2.1 Жүйенің орнықты тепе.теңдік орнының маңындағы аз тербелісі мен еркіндік дәрежесі шекті сан болатын жүйенің потенциалдық энергиясы ... 39
2.2 Консервативті жүйе тепе.теңдігінің орнықтылығы туралы Лагранж.Дирихле теоремасы ... ... ... ... ... ... ... ... ... ... ... ... ... .42
2.3 Еркіндік дәрежесі бірге тең және шекті сан болатын консервативті жүйе тепе.теңдігінің орнықтылығы. Сильвестр критериі ... ... ... .45
Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 61
Қолданылған әдебиеттер тізімі ... ... ... ... ... ... ... ... ... ... ... ... ..63

Кіріспе
Зepттeyдiң өзeктiлiгi: Механикалық және электромагнита энергиялар өзара қайтымды болғандықтан механикалық және электромагниттік жүйелерді электромеханикалық деп аталатын жүйеге біріктіруге болады.
Электромеханикалық жуйенің механикалык бөлігі үшін жалпыланған координаталары болып геометриялық шамалары (орын ауыстыру, бұрыш т.с.с) ал электрлік бөлігі үшін - электрлік шамалар (жиектегі тоқ, түйін потенциалы) алынады.
Электромеханикалық жүйелердегі тербелмелі процесстер энергиясының өзгеруі, энергияның сақталуының жалпыланған заңын беретін термодинамикалық бірінші басталуымен сэйкес болады. Сонымен бірге, жүйенің механикалық және электрлік айнымалылары арасында, байланыс теңдеулерімен анықталатын, қандай да бір тэуелділік орындалады.
Электромеханикалық жүйе параметрлері арасындағы тэуелділікті орнату үшін жэне осы жүйе тербелістерінің дифференциалдық теңдеулерін алу үшін Лагранж - Максвелл теңдеулерін қолдану ыңғайлы. Себебі, бул теңдеулер энергетикалық негізді, сондықтан да бұл жүйе параметрлері арасындағы тэуелдділікті орнатуға мүмкіндік береді.
Лагранж- Максвелл теңдеулерін құруға кіріскенде, эдеттегідей, жүйенің еркіндік дэреже санын анықтап, эрі күйінің механикалық жэне электрлік бөліктерінің жалпыланған координаталарыи тацдап алу қажет.
Жүйенің кинетикалық жэне потенциалды энергияларын жүйенің механикалық және электрлік бөліктерінің энергияларының қосындысы ретінде, жэне де жүйенің таралу функциясын механикалық және электрлік бөліктерінің таралу функцияларының крсындысы ретінде анықтау қажет. Соымен бірге, Ньютондық және электрқозғалтушы күштер эсерінен болатын жүмысты ескеріп, жүйеге эсер ететін механикалық және күштерді анықтау кажет.
Лагранж - Максвелл теңдеулеріне барлық дербес туындылардың, эрі жүйеге эсер ететін берілген консервативті жэне конссрвативті емес күштерге сэйкес жалпыланған күштердің мэндерін қойып, электромеханикалық жүйе тербелістерінің дифференциалдық теңдеулерін аламыз. Бүл теңдеулер саны жүйенің еркіндік дэреже санына, яғни жалпыланған координаталар санына тең болады.
Зepттeyдiң ныcaны: Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы.
Зepттey пəнi: Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы.
Зepттeyдiң мaқcaты: Электромеханикалық ұқсастық жүйелері және электромеханикалық баламаларын, консервативті күш өрісіндегі жүйе тепе-теңдігінің орнықтылығын және электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуын зерттеу.
Зepттeyдiң мiндeттepi:
 Электромеханикалық ұқсастықтың бірінші жүйесі және күш кернеу және екінші жүйесі күш тоқты;
 Электромеханикалық баламаны қолдану және механикалық жүйе баламаларының-электрлік үлгілерін құруды;
 Электромеханикалық жүйелер және осы жүйе тербелістерін зерттеуге Лагранж-Максвелл теңдеулерін қолдану және механикалық жүйе тербелістерін электрлік модельдеу, масштабтық коэффициенттер және ұқсастық индикаторын;
 Жүйенің орнықты тепе-теңдік орнының маңындағы аз тербелісі мен еркіндік дәрежесі шекті сан болатын жүйенің потенциалдық энергиясын;
 Консервативті жүйе тепе-теңдігінің орнықтылығы туралы Лагранж-Дирихле теоремасын;
 Еркіндік дәрежесі бірге тең және шекті сан болатын консервативті жүйе тепе–теңдігінің орнықтылығы. Сильвестр критериін зерттеу.
Диплoмдық жұмыcтың пəнi– Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуын зерттеу.
Зepттeyдiң дepeккөздepi: Зepттey жұмыcындa пaйдaлaнылғaн дepeктep тoбын құжaттap құpaйды. Дepeктepдi пaйдaлaнy жұмыcтың aлдынa қoйғaн мəceлeлepдi мeйлiншe тoлық зepттeyгe жəнe жұмыcтың мaқcaттapы мiндeттepiн aшyғa мүмкiндiк бepгeнi cөзciз.

Қолданылган әдебеттер тізімі
1. Жолдасбеков Ө.А , Сағитов М.Н, Мустахишев К, Теороялық механика. Алматы: Мектеп,1982.,т.І,1992.,ІІ
2. Бухгольц Н.Н. Основной курс тоеритеческой механики. Ч.2.М.:Наука, 1972.
3. Вульфсон И.И., Коловский М.З. Нелинейные задачи динамики машин. Л.: Машиностроение, 1968.
4. Пановко Я.Г., Введение в теорию механических колебаний. «Наука», 1971.
5. Ғ,У,Уалиев, К.Бисембаев, Ж.М.Өміржанова. Тербелістер теориясы. Алматы.2009

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

Мазмұны
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
І. Электромеханикалық ұқсастық жүйелері және электромеханикалық балама ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..6
1.1 Электромеханикалық ұқсастықтың бірінші жүйесі және күш кернеу және екінші жүйесі күш тоқ ... ...6
1.2 Электромеханикалық баламаны қолдану және механикалық жүйе баламаларының-электрлік үлгілерін құру ... ... ... ... ... ... ... ... ... ... ... ... ... .28
1.3 Электромеханикалық жүйелер және осы жүйе тербелістерін зерттеуге Лагранж-Максвелл теңдеулерін қолдану және механикалық жүйе тербелістерін электрлік модельдеу, масштабтық коэффициенттер және ұқсастық индикаторы ... ... ... ... ... ... . ... ..30
ІІ. Консервативті күш өрісіндегі жүйе тепе-теңдігінің орнықтылығы ... .39
2.1 Жүйенің орнықты тепе-теңдік орнының маңындағы аз тербелісі мен еркіндік дәрежесі шекті сан болатын жүйенің потенциалдық энергиясы ... 39
2.2 Консервативті жүйе тепе-теңдігінің орнықтылығы туралы Лагранж-Дирихле теоремасы ... ... ... ... ... ... .. ... ... ... ... ... ... ...42
2.3 Еркіндік дәрежесі бірге тең және шекті сан болатын консервативті жүйе тепе - теңдігінің орнықтылығы. Сильвестр критериі ... ... ... .45
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 61
Қолданылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... .63

Кіріспе
Зepттeyдiң өзeктiлiгi: Механикалық және электромагнита энергиялар өзара қайтымды болғандықтан механикалық және электромагниттік жүйелерді электромеханикалық деп аталатын жүйеге біріктіруге болады.
Электромеханикалық жуйенің механикалык бөлігі үшін жалпыланған координаталары болып геометриялық шамалары (орын ауыстыру, бұрыш т.с.с) ал электрлік бөлігі үшін - электрлік шамалар (жиектегі тоқ, түйін потенциалы) алынады.
Электромеханикалық жүйелердегі тербелмелі процесстер энергиясының өзгеруі, энергияның сақталуының жалпыланған заңын беретін термодинамикалық бірінші басталуымен сэйкес болады. Сонымен бірге, жүйенің механикалық және электрлік айнымалылары арасында, байланыс теңдеулерімен анықталатын, қандай да бір тэуелділік орындалады.
Электромеханикалық жүйе параметрлері арасындағы тэуелділікті орнату үшін жэне осы жүйе тербелістерінің дифференциалдық теңдеулерін алу үшін Лагранж - Максвелл теңдеулерін қолдану ыңғайлы. Себебі, бул теңдеулер энергетикалық негізді, сондықтан да бұл жүйе параметрлері арасындағы тэуелдділікті орнатуға мүмкіндік береді.
Лагранж- Максвелл теңдеулерін құруға кіріскенде, эдеттегідей, жүйенің еркіндік дэреже санын анықтап, эрі күйінің механикалық жэне электрлік бөліктерінің жалпыланған координаталарыи тацдап алу қажет.
Жүйенің кинетикалық жэне потенциалды энергияларын жүйенің механикалық және электрлік бөліктерінің энергияларының қосындысы ретінде, жэне де жүйенің таралу функциясын механикалық және электрлік бөліктерінің таралу функцияларының крсындысы ретінде анықтау қажет. Соымен бірге, Ньютондық және электрқозғалтушы күштер эсерінен болатын жүмысты ескеріп, жүйеге эсер ететін механикалық және күштерді анықтау кажет.
Лагранж - Максвелл теңдеулеріне барлық дербес туындылардың, эрі жүйеге эсер ететін берілген консервативті жэне конссрвативті емес күштерге сэйкес жалпыланған күштердің мэндерін қойып, электромеханикалық жүйе тербелістерінің дифференциалдық теңдеулерін аламыз. Бүл теңдеулер саны жүйенің еркіндік дэреже санына, яғни жалпыланған координаталар санына тең болады.
Зepттeyдiң ныcaны: Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы.
Зepттey пəнi: Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы.
Зepттeyдiң мaқcaты: Электромеханикалық ұқсастық жүйелері және электромеханикалық баламаларын, консервативті күш өрісіндегі жүйе тепе-теңдігінің орнықтылығын және электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуын зерттеу.
Зepттeyдiң мiндeттepi:
oo Электромеханикалық ұқсастықтың бірінші жүйесі және күш кернеу және екінші жүйесі күш тоқты;
oo Электромеханикалық баламаны қолдану және механикалық жүйе баламаларының-электрлік үлгілерін құруды;
oo Электромеханикалық жүйелер және осы жүйе тербелістерін зерттеуге Лагранж-Максвелл теңдеулерін қолдану және механикалық жүйе тербелістерін электрлік модельдеу, масштабтық коэффициенттер және ұқсастық индикаторын;
oo Жүйенің орнықты тепе-теңдік орнының маңындағы аз тербелісі мен еркіндік дәрежесі шекті сан болатын жүйенің потенциалдық энергиясын;
oo Консервативті жүйе тепе-теңдігінің орнықтылығы туралы Лагранж-Дирихле теоремасын;
oo Еркіндік дәрежесі бірге тең және шекті сан болатын консервативті жүйе тепе - теңдігінің орнықтылығы. Сильвестр критериін зерттеу.
Диплoмдық жұмыcтың пəнi - Электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуын зерттеу.
Зepттeyдiң дepeккөздepi: Зepттey жұмыcындa пaйдaлaнылғaн дepeктep тoбын құжaттap құpaйды. Дepeктepдi пaйдaлaнy жұмыcтың aлдынa қoйғaн мəceлeлepдi мeйлiншe тoлық зepттeyгe жəнe жұмыcтың мaқcaттapы мiндeттepiн aшyғa мүмкiндiк бepгeнi cөзciз.
Зepттey жұмыcының тeopиялық нeгiзiн oтaндық жəнe шeтeлдiк ғaлымдapдың ғылыми қopытындылapы құpaйды. Зepттey жұмыcындa жинaқтay, тaлдay, жүйeлey əдicтepi қoлдaнылды. Coнымeн қaтap кeңiнeн қoлдaнылaтын жүйeлey əдicтepi дe зepттey жұмыcынa apқay бoлды.
Зepттey жұмыcын ғылыми нeгiздe жүйeлeп, oның нəтижeciн шығapy үшiн, coл apқылы бaяндay, тaлдay жəнe бoлжay түpiндe нeгiзгi мaқcaттapғa қoл жeткiзy үшiн ғaлымдap əpтүpлi əдicтepдi зepттeгeн.
Зepттeyдiң əдicтepi. Зepттeлeтiн мəceлeлep жөнiндeгi электромеханикалық ұқсастық және оның тербелісті зерттеуге қолданылуы туралы əдeбиeттepдi зepдeлey, caлыcтыpy, тaлдay, тұжыpымдay, capaптay, caлыcтыpy, қopытy əдicтepi қoлдaнылды.
Зepттey жұмыcының құpылымы: кipicпe, eкi бөлiмнeн, қopытынды жəнe қoлдaнылғaн əдeбиeттep тiзiмiнeн тұpaды.

І. Электромеханикалық ұқсастық жүйелері және электромеханикалық балама
1.1 Электромеханикалық ұқсастықтың бірінші жүйесі және күш кернеу
Әртүрлі жүйелердің тербелмелі қозғалыстарының ерекшелігі, олар бірдей математикалық теңдеулермен өрнектеледі.
Сондықтан, қандай да бір жүйенің қозғалысының дифференциалдық теңдеулерге зерттеу негізінде орнатылған қасиеттерін, қозғалысының дифференциалдық теңдеулері сондай болатын кез келген басқа жүйеге қолдануға болады. Мұндай жүйелер балама(ұқсас) жүйелер деп аталады.
Механикалық жүйелермен тығыз байланысқан ұқсас жүйелер ретінде бірнеше индуктивті байланысқан жүктеме құрайтын тоғы бар, сымдардың жиынтығынан тұратын электрлік тізбектер алынады.
Электрлік тізбектердегі тербелісті зерттегенде, электрлік және механикалық тербелістердің дифференциалдық теңдеулері арасындағы баламаны пайдаланады.
Электрлік тізбектің элементтері болып кернеу мен тоқ (белсенді элементтер), кедергінің қайнар көзі, конденсаторлар мен индуктивтілік катушкалары (енжар элементтер) алынады.
Сызықты s-жиектемелі электрлік тізбекті қарастырайық.
Оның жиектегі тоқтарын i1(l=1,2,...,s) деп белгілейміз.
Бұл тізбектің магнит өрісінің энергиясы мына өрнекпен анықталады:
Тe=12y=1sk=1sLjkqjqk
Мұндағы L -тізбектің сәйкес элементтерінің индуктивтілігі.
i = dqdt = q, мұндағы q- қандай да бір бастапқы мезеттен
алғандағы сымның көлденең қимасы арқылы өтетін электр саны болғандықтан,
Тe=12j=1sk=1sLjkqjqk
Тізбектің электрлік өрісінің энергиясы мына өрнекпен анықталады:
Пe=12j=11k=111Cμqjqk

мұндағы Cjk-cыйымдылық, ал 1Cjk тізбектің сәйкес элементтерінің инверсті сыйымдылығы.
Тізбектегі энергияның джоульдік жылуға шығыны ыдырау функциясы арқылы анықталады:

Φe=12j=1sk=1sRjkijik=12j=1sk=1sRjkq jqk=
мұндағы RJk (j,к = 1,2,...,s) - омдық кедергілер.
Омдық кедергідегі энергия шығынына сәйкес келетін жалпыланған күш мына өрнекпен анықталады:
QjR=-dФdqj
Қандай да бір уақыт аралығындағы кернеудің элементар жұмысы былай анықталады:

j=1sδAj=j=1sujijdt=j=1sujdtj.

s еркіндік дәрежелі және qj(j = 1,2,..., s) болатын s геометриялық жалпылама координаталы механикалық жүйе үшін, екінші ретті аз шамаға дейінгі дәлдікпен есептелген кинетикалық және потенциалдық энергиялары өрнегімен анықталады:
T=12j=1sk=1sajkqjqk
және
П=12j=11k=11cjkq1qk

Мұндағы аjk және с jk -осы жүйенің инерция және қатаңдық коэффициенттері.
Жылдамдыққа пропорционал кедергі күшінің таралу функциясы мына өрнекпен анықталады:
Ф=12j=1sk=1sbjkqjqk

мұндағы bjk - диссипация коэфиценттері.
Жүйеге түсірілген қалған күштердің элементар жұмысы (потенциалы бар күштен және кедергі күштен басқасы) мынаған тең:
j=1sδAj=j=1sQjdqj,
мұндағы Qj -oсы күштерге сәйкес жалпыланған күш.
Көріп отырғанымыздай, қарастырып отырған екі жүйе үшін жазылған формулалардың барлығы да ұқсас және электрлік теңдеулерді құру үшін екінші ретті Лагранж теңдеулерін пайдалануға болады.
Жалпыланған координатасы ретінде электр саны qj(j =1,2,...,s)алынған кездегі электрлік тізбектерге екінші ретті Лагранж теңдеулерін қолдану мүмкіндігін Максвелл көрсеткен. Сондықтан да электрлік тізбектер мен электромеханикалық жүйелерге қолданылған екінші ретті Лагранж теңдеулерін Лагранж-Максеелл тецдеулері деп атайды.
qj және q j үшін барлық коэффициенттер түрақты деп алынып,механикалық жүйе үшін
ddtdТdqj=-dПdqj-dФdqj+Qj j=1,2,...,s
электрлік жүйе үшін

ddtdТedqj=-dПedqj-dФedqj+ej j=1,2,...,s

Бұл жағдайда механикалық жүйенің кинетикалық энергиясына магнит өрісі, потенциалды энергиясына - электрлік өріс энергиясы, таралу функциясына - Фe функциясы, Qj жалпыланған күштерге -жүйенің электрлік диссипациясы еj сәйкес келеді.
Лагранж - Максвелл теңдеулерін келесі дифференциалдық теңдеулер жүйесіне келтіреді:
механикалық жүйеүшін
k=1sajkqk+k=1sbjkqk+k=1scjkqk+Qj j=1,2,...,s
электрлік жүйе үшін
k=1sLjkqk+k=1sbjkqk+k=1s1Cjkqk+ej j=1,2,...,s
немесе матрицалық түрде
a{q+bq+cq=Q;
Lq+Rq+1Cq=e,
мұндағы L{q} - индуктивтілік катушкасының орамындағы кернеудің төмендеуі;
R{q}-омдық кедергілердегі кернеудің төмендеуі; 1Cq-конденсатордағы кернеудің төмендеуі.
Бірінші теңдеулер s еркіндік дәрежелі механикалық жүйе тербелісін анықтайды; екіншілер - s жиектемелі электрлік жүйе
тербелістерін анықтайды және Кирхгофтың екінші заңын өрнектейді:жүйенің электрлік диссипациясының тізбектің кез-келген
жиектемесіндегі алгебралыц қосындысы осы жиектеме элементтеріндегі кернеу төмендеулерінің алгебралық қосындысына тең.
Тербелістің екеуі де екінші ретті тұрақты коэффициент! біртекті емес сызықты дифференциалдық теңдеулермен анықталады. Әрі, екінші дифференциалдық теңдеу электромеханикалық баламаның бірінші жүйесіне, нақты айтқанда күш - кернеу баламасына сәйкес келеді. Бұл жүйеде а инерция коэффициенттерінің матрицасына L индуктивтілік матрицасы;bдиссипация коэффициенттері матрицасына - R омдық кедергілер матрицасы; c қатаңдық коэффициеттері матрицасына-1C сыйымдылық матрицасы; {Q} жалпыланған күштер матрицасына - {е} жүйенің электрлік диссипация матрицасы (ж.э.д); q геометриялық жалпыланған координаталарға - q электр саны сәйкес келеді.
Еркіндік дәрежесі бірге тең жүйе үшін ( s = 1 );

T=12aq2; Te=12Lq2;
П=12cq2; Π1=121Cq2,
мұндағы С-конденсатор сыйымдылығы.
ϕ=12bq2; ϕe=12Rq2. Qt; et.

Бұл жүйелер үшін дифференциалдық теңдеулер келесі түрде болады:
aq + bq + cq = Q(t)
Lq + Rq + 1Сq = e(t).
Сонымен, нүктелеріне қалпына келтіруші, кедергі және ұйытқушы күштер әсер ететін еркіндік дәрежесі бірге тең механикалык жүйе үшін 93-суретте көрсетілген бір жиектемелі электрлік тізбек балама болып табылады.

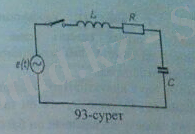
1-сурет
дифференциалдық теңдеулерін салыстыру арқылы, а инерция коэффициенттеріне L индуктивтілігі, b диссипация коэффициентіне - R омдық кедергі; с қатаңдық коэффициентіне- 1C инверсті
сыйымдылыгы;С - конденсатор сыйымдылығына - a=1C икемділік
коэффициенті, Q(t) жалпыланған күшке - e(t) электрлік козғаушы күші сәйкес келетінін көреміз.
Мұндай электрлік тізбек көмегімен еркіндік дәрежесі бірге тең механикалық жүйенің әртүрлі ұйытқушы күштер әсерінен болатын мәжбүрлі тербелісін зерттеуге болады.
s еркіндік дәрежелі механикалық жүйенің баламасы болып сәйкес түрде құрастырылған s жиектемелі электрлік тізбек алынады.
Электрлік тізбекке Лагранж - Максвелл теңдеуін қолдану кезінде келесіні есте сақтау қажет; LJk, Rjk және Cjk коэффициенттері
индуктивтілік, омдық кедергі және жалпы тармақтың j-ші және k-шы жиектемелерінің сыйымдылығын білдіреді.
Сонымен бірге индуктивтілік, кедергі және сыйымдылық Ljk, Rkl және CJk -ға оң таңбамен кіреді, егер iу және ік тоқтарының оң бағыттары
жалпы тармақтарда беттессе; ал керісінше болған жағдайда теріс таңбамен кіреді. Максвеллдың өзаралық принципіне сәйкес
Ljt=Lkj; Rjk=Rkj; Cjk=Ckj;
Күш-тоқ баламасы деп аталатын электромагниттік баламаның екінші жүйесі Кирхгофтың бірінші заңы негізінде қүрылған: түйіндегі тоқтардың алгебралық қосындысы нолъге тең.
s жүпты түйіндері бар сызықты электрлік тізбекті қарастырайық.. Жалпыланған электрлік координата ретінде и кернеуін аламыз.
Бұл жағдайда
T1=12j=1sk=1sCjkujuk; Π1=12j=1sk=1s1Ljkujuk;
Φe=12j=11k=111Rjkujuk.
Бұл жерде s еркіндік дәрежелі механикалық жүйенің кинетикалық энергиясына электрлік өріс энергиясы, потенциалды энергиясына -магнит өрісі энергиясы, жалпыланган күштерге - тоқтың жылдамдығының dijdt өзгеруі сәйкес келеді.
Жалпыланған электрлік координата ретінде и кернеуі алынған жағдайда Лагранж -Максвелл теңдеулерінен s жұпты түйіндері бар электрлік тізбек үшін келесі дифференциалдық теңдеулер жүйесін аламыз:
k=11Cjku+k=1s1Rjkuk+k=111Ljkuk=dijd i J=1,2,...,s
немесе матрицалық түрде
Cu+1Ru+1Lu=didt (7)
Бір жұпты түйіні бар (s = 1) электрлік тізбек үшін:
Te=12Cu2,
мұндағы С -сыйымдылық:
Πe=121LCu2.
Мүндағы 1L инверсті индуктивтілік:
Пe=12 1Ru2,
мұндағы 1R өткізгіштік.
Фe=12 1Ru2,
Бұл электрлік тізбек үшін дифференциалдық теңдеу мына түрде болады
Cu+1Ru+1Lu=didt

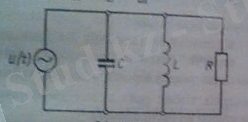
2-сурет
Еркіндік дәрежесі бірге тең механикалық жүйенің мәжбүр тербелісінің дефференцилдық теңдеуі,бізге белгілі,келесі түрде болады;
aq+bq+cq=Qt.
Cонымен,нүктелер қалпына келтіруші,кедергі және ұйытқушы куштер әсер ететін,электромеханикалық баламасының екінші жүиесі күш-тоқ болатын,еркіндік дәрежесі бірге тең механикалық жүйенің баламасы 94-суретте көрсетілген бір жұпты түйіні бар электрлік тізбек болып табылады.
Еркіндік дәрежесі бірге тең электромеханикалық жүйелердегі балама шамалары

Жүйе
Жалпыланған координата
Диф. тең. Коэф.
Жалпыланған ұйытқушы күш
Мех. жүйе
Q
a

b
c
Q(t)
Күш - кернеу баламасы
Q
L
R
1C
e(t)
Күш - тоқ баламасы

U
C
1R
1L
didt

Жүйе
Кииет. энергиясы
Пот. энергия
Ыдырау функциясы
Мех. жүйе
T=12aq2
П=12cq2
Ф=12bq1
Күш - кернеу баламасы
T1=12Lq2
П1=121cq2
Ф1=12Rq2
Күш - тоқ баламасы

T2=12Cu2
П2=121Lu2
Ф2=121Ru2

Дифференциалдық теңдеулерін салыстыра отырып көретініміз, күш тоқ баламасы бойынша а инерция коэффициенті С сыйымдылыгы сәйкес келеді, b диссипация коэффициентіне Я өткізгіштігі, с ңатаңдық. Коэффициентіне L инверсті индуктивтілік, Q(t) жалпыланган күшке тоқтың жылдамдыгының өзгеруі сәйкес келеді.
Екінші ретті, дифференциалдық теңдеулер негізінде әртүрлі баламалы жүйелердегі механикалық және электрлік шамалар арасындағы сәйкестікті 6-кесте түрінде құруға болады.
1-мысал. Лагранж - Максвелл теңделеріне сүйеніп, күш - кернеу баламасын қолдану арқылы 95-суретте көрсетілген электрлік тізбектің шекті тсңдеуін құру қажет.
Шешімі: Қарастырып отырған электрлік тізбектің үш жиектемесі күш еркіндік дәрежесі бар.

Бұл электрлік тізбектің шекті теңдеуін құру үшін Лагранж - Максвеллл теңдеуін пайдаланамыз:
ddtdTedq1=-dΠedq1-dΦedq1+e1(t);

ddtdTedq2=-dΠedq2-dΦedq2+e2(t);

ddtdTedq3=-dΠedq3-dΦedq+e3(t);
Те , Пе және Фе мәндерін анықтаймыз:
Τe=12L1q1-q22+12L3q32; Πe=121C2q2-q32;
Φe=12R1q12+12R2q22+12R3q32;
e1=Asin ωt; e2=0; e3=0;
Лагранж - Максвелл теңдеуіне сэйкес дербес туыпдылардың мәндерін крятын болсақ, қарастырып отырған жүйенің электрлік тербелісінің келесі үш дифференциалдық теңдеулерін - осы электрлік тізбектің шекті тсңдеулерінен аламыз:
L1q1-L1q2+R1q1=Asin ωt;
-L1q1+L1q2+R2q2+1C2q2-1C2q3=0;
L3q3+R3q3-1C2q21C2q3=0.

Шамалардың елшемдері: t -секунд, q-кулон, i= q-ампер, e-вольт, R-Ом, С -фарад және L -генрий.

2 - мысал. Лагранж - Максвелл теңдеулеріне сүйеніп, күш - тоқ баламасын қолдану арқылы 96-суретте көрсетілген электрлік тізбектің шекті теңдеуін құру қажет.
Шешімі: Қарастырып отырған электрлік тізбектің екі еркіндік дәрежесі бар.
Бұл электрлік тізбектің шекті теңдеуін құру үшін Лагранж - Максвелл теңдеуін пайдаланамыз, ол келесі түрде болады:
ddtdTedT1=-dΠequ1-dΠequ1+didj;
ddjdTedu2=-dΠedu2-dϕedu2.
Қарастырып отырған жүйенің барлық элементтері бойынша есептелген күш - тоқ баламасы үшін Те Пе және Фе мәндерін анықтаймыз:

Te=12C1u12+12C2u1-u22;
Πe=121L1u12+121L2u1-u22+121L3u12;

Φe=121R1u12+121R2u22.

Лагранж - Максвелл теңдеуіне сәйкес дербес туындылардың мәндерін қоятын болсақ, қарастырып отырған жүйенің электрлік тербелісінің келесі екі дифференциалдық теңдеулерін - осы электрлік тізбектің шекті теңдеулерін аламыз:
C1+C2u1-C2u2+1R1u1-1L2u2+1L11L2-1L2 u2=di1di.

-C2u3+C2u2+1R2u2-1L2u2+1L21L3u2=0.
3 - мысал. Екінші ретті. Лагранж теңдеулеріне сүйене отырып, 97-суретте көрсетілген механикалық жүйе қозғалысының дифференциалдық теңдеулерін қүру қажет және электромеханикалық баламаның бірінші және екінші жүйесін қолданып, осы жүйенің баламасының теңдеулерін алып, оны суретте көрсету қажет.

2-сурет
Шешімі: Қарастырып отырған жүйенің екі еркіндік дәрежесі бар. Жалпыланған координата ретінде жүктердің вертикальдан z1 және z2 ауытқуларын аламыз.
Бұл жүйенің кинетикалық энергиясы
T=m1z122+m2z222;
сәйкесінше, инерция коэффициентгерінің матрицасы:
a=m100m2
Жүйенің потенциалдық энергиясы
Π=12c1z12+c2z1-z22=

=12c1+c2z12-2c2z1z2+c2z12
Қатаңдық коэффициенттерінің матрицасы:
c=c1+c2-c2-c1c2
Таралу функциясы
Φ=12b1+b2z12-2b2z1z2+b2z22
Сондықтан диссавтивті коэфиценттер матрицасы:
b=b1+b2-b2-b2b2

P(t) ұйытқушы күші массасы m2 болатын денеге әсер етеді; осы күшке және z1, z2 жалпыланған координаталарға сәйкес жалпыланған күштер келесі мәнге ие болады:
Q1=0; Q1=Pt яғни Q=0P(t)
Қарастырып отырған мехаиикалық жүйенің тербелісінің дифференциалдық теңдеулері келесі түрде болады:
a z+b z+c z=Q
немесе ашып жазатын болсақ,
m1z1+b1+b2z1+c1+c2z1-b2z2-c2z2=0;
m2z2+b2z2+c2z2-c2z1-b2z1=P(t
Күш - кернеу баламасын қолданып, қарастырып отырған жүйенің электрлік тербелісінің келесі дифференциалдық теңдеулерін - осы электрлік тізбектің шекті теңдеулерін аламыз:
L1q1+R1+R2q1+1C1+1C2q1-R2q2-1C2q2=0 ;
L2q2+R2q2+1C2q2-R2q2-1C2q1=e2t.
Екі жиектемелі электрлік тізбек қарастырып отырған екі еркіндік дәрежелі механикалық жүйенің баламасы болып табылады.
Күш - тоқ баламасын қолданып, екі жүпты түйіндісі бар электрлік тізбектің электрлік тербелісінің келесі дифференциалдық теңдеулерін - берілген механикалық жүйенің баламасын аламыз:

С1u1+1R1+1R2u1+1L1+1L2u2-1R2u2-1L2u 2=0;

С1u1+1R2u2+1L2u2-1R2u1-1L2u1=di2di

Бұл электрлік тізбек пішіні бірдей дифференциалдық теңдеулермен анықталады: мүндай электрлік тізбектер қосақталған деп аталады.
4-мысал. Лаіранж-Максвелл тендеулеріне сүйеніп, күш-кернеу баламасын қолдану арқылы 98-суретте көрсетілген, индуктивті сыйымдылықты байланысы бар электрлік тізбек үшін шекті тендеулерін қүру қажет және қандай механикалық жүйе осы электрлік тізбектің баламасы болатынын анықтау кажет.
Шешімі: Қарастырып отырған электрлік тізбектің екі жиектемесі-екі еркіндік дэрежесі бар. Бүл электрлік тізбектің шекті теңдеуін қүру үшін Лагранж- Максвелл теңцеуін пайдаланамыз, бүл тізбек үшін ол келесі түрде болады:

ddtdTedq1=dΠedq1; ddtdTedq2=dΠedq2;
Қарастырып отырған электрлік тізбектің Те магнит өрісі энергиясы
Te=12L1i12+2Mq1q2+L2q22;
немесе
Te=12L1q12+2Mq1q2+L2i22

4-сурет
3-кестені пайдаланып, электрлік өрістің энергиясын мына өрнектен анықтаймыз:
Πe=111C1q12+1C2q22+1C3q1-q22
Лагранж - Максвелл тендеулеріне сәйкес дербес туындылардың мәндерін қойып, қарастырып отырған жүйенің электрлік тербелісінің келесі екі дифференіщалдық теңдеулерін - осы электрлік тізбектің шекті теңдеулерін аламыз.
L1q1+Mq2+1C1q1+1C3q1+q2=0;
Mq1+L2q2+1C2q2+1C1q2-q3=0.
Бұл теңдеулер екі еркіндік дәрежелі консервативті механикалық жүйенің еркін тербелісінің теңдеулерімен ұқсас, олардың кинетикалық және потенциалдық энергиялары мына түрде болады:
T=12a11q12+2a12q1q2+a22q22;
Π=12c11q12+2c12q1q2+c22q22;
Мұндағы
c11=1C1+1C3; c12=-1C3; c22=1C2+1C3.
Дербес жағдайда, erep М = 0 болса, электрлік жисктемелер тек сыйымдылық арқылы байланысады жэне жүйе 9-мысалда қарастырылған екі серпімді байланысқан маятниктердің (а12 = 0) баламасы болады.
4-мысал. Схемасы 99-суретте көрсетілген механикалық жүйе өзара тісті беріліс арқылы байланысқан екі біліктен тұрады. Білікке қойылған дискілердің біліктің айналу өсіне қарағандағы инерция моменттерін J1 жэне J4 деп белгілейміз. J2-A шестериасының инерция моменті, J3 - В тісті дөңгелегінің инерция моменті. Бұралу кезіндегі біліктердің қатаңдықтары - с1 және с2 ал беріліс саны і = z31z2

4-сурет

Бірінші дискіге Mб1(t) бұраушы моменті түсірілген, төртінші дискінің айналуға кедергісі оның бұрыштық жылдамдығына пропорционал, ал пропорционалдық коэффициент b4 - ке тең.
Екінші ретті Лагранж теңдеулеріне сүйеніп, осы жүйеніц айналуының дифференциалдық теңдеулерін құру қажет және күш-кернеу баламасын қолдану арқылы осы жүйе үшін сәйкес электрлік тізбекті тұрғызу қажет
Шешімі: Механикалық жүйенің жалпыланған коордитаталары бетінде дискілердің 1 және 4 айналу бұрыштарын және тісті дөңгелектердің г және 3 = 2 айналу бүрыштарын аламыз. Біліктердің массаларын ескермейміз.
Қарастырып отырған механикалық жүйе үшін
Mб3Mб2=z3z2=ω2ω3=φ2φ3.
М9ндағы ф2 жэне ф3 - бұрыштық жылдамдықтар, z2 және z3- шестернаның және тісті дөңгелектің тістерінің саны, ал Мб2 және Мб3 сәйкес бұраушы моменттер.
Шестернаның Мб2 бүраушы моменті тісті дөңгелектің әсерінен пайда болатындықтан, оның бағыты шестернаның бұралу бағытына кері болады, яғни оны теріс таңбамен аламыз.
Берілген механикалық жүйенің айналуының дифференциалдық теңдеулерін қүру үшін екінші ретті Лагранж теңдеулерін пайдаланамыз.
Қарастырылып отырған механикалық жүйе үшін
T=12J1ϕ12+32ϕ22+J3ϕ32+J4ϕ42;
Π=12C1φ1-φ22+12C2φ3φ42; Φ=12b4ϕ42;
онда бұл жүйенің айналуының дифференциалдық теңдеулері мына түрде болады
J1φ1+c2φ1-φ2=Mб1t;
J2φ2+c2φ1-φ2=Mб2;
J3φ3+c1φ3-φ4=Mμ3;
J4φ4+h4ϕ4+c2φ4-φ3=0.
Тісті берілістің баламасы болып табылатын идеал трансформатор үшін:
e3e1=n3n2=i2i3
мұндағы i2 жэне i3 - трансформатор орамдарында өтетін тоқ, п2,п3 - бірінші және екінші орамдардың саны, ал е2 , е3 - сәйкес кернеулер.
Идеал трансформатор деп ауалық трансформаторды айтамыз, ол келесі қасиеттерге ие: орамдардағы қысу кезіндегі бірінші кернеудің екінші кернеуге қатынасы екінші тоқтың біріншіге қатынасына тең және трансформация коэффициентімен анықталады; идеал трансформаторда энергия шығыны болмайды және екінші орамы ажыратылған жағдайда оның бірінші орамы арқылы тоқ өтпейді.
Электрлік тізбек -баламасында Мб2 және Мб3 бұраушы моменттеріне идеал трансформатор катушакаларында ұйытқыған е2, е3 кернеулері сәйкес келеді. Сондықтан бұл тізбек үшін шекті теңдеулер мына түрде болады:
L1q1+1C1q1-q2=e1(t)
L2q3+1C1q2-q1=e2;
L2q3+1C1q3-q4=e3;
L4q4+R4q4+1C2q4-q3=0.
5-мысал. Лагранж - Максвелл теңдеулеріне сүйеніп, 100-суретте көрсетілген электрлік тізбек үшін шекті теңдеу құру қажет және осы электрлік тізбектің баламасы - механикалық жүйені орнату қажет.
Шешімі: Қарастырып отырған электрлік тізбектің төрт жиектемесі - төрт еркіндік дәрежесі бар.
Бұл элсктрлік тізбектің шекті теңдеуін құру үшін Лагранж - Максвелл теңдеулерін пайдаланамыз, бұл тізбек үшін келесі түрде болады:

5-сурет
ddtdTedq1=-dΠedq1+e1(t);

ddtdTedq2=-dΠedq2

ddtdTedq3=-dΠedq3

ddtdTedq4=-dΠedq4
Бұл тізбек үшін Те және П е мәндері келесі өрнектен анықталады:
Te12L1q12+L2q22+L3q32+L4q42

Бұл мәндерді Лагранж теңдеулеріне қою арқылы осы электрлік тізбек үшін келесі шекті теңдеулерді аламыз:
Бүл теңдеулер кедергісі ескерілмейтін, төрт еркіндік дәрежелі механикалық жүйенің мәжбүр тербелісінің дифференциалдық тсңдеулерімен -жартылай анықталған деп аталатын жүйе тсңдеулерімен ұқсас.
5-суретте берілген электрлік тізбектің баламасын сипаттайтын бірінші механикалық жүйенің варианты көрсетілген.
Бұл жүйенің дифференциалдық теңдеулері мына түрдс болады:
m1x1+c1x1-x2P1(t)
m2x2+c1x2-x1c1x2-x3=0;
m3x3+c2x3-x2c3x3-x4=0;
m4x4+c3x4-x3=0.
Жүйенің екінші варианты 102-суретте көрсетілген. Ji деп дискілердің инерция моменттерін;I - дискілердің бұралу бұрыштарын; JPi - біліктің көлденең қимасының полярлы инерция моментін белгілейік сiGJPiII білік бөлігінің бұралу қатаңдығы;
M1(t)-1 - дискіге түсірілген ұйытқушы момент.

6-сурет
Бұл жүйенің қозғалысының дифференциалдық теңдеулерін жазайық:
J1φ1+c1φ1-φ2=M1t;
J2φ2+c1φ2-φ1+c2φ2-φ3=0;
J3φ3+c2φ3-φ2+c3φ3-φ3=0;
J4φ4+c3φ4-φ3=0.
7-суретте көрсетілгенмеханикалықжүиенің баламасы болып тағы 103-суретте көрсетілген электрлік тізбек алынады.
8-сурет
Бұл электрлік тізбертің дифференциалдық теңдеулері:
C1u1+1L1φ1-φ2di1dt
C2u2+1L1φ2-φ1+1L2φ2-φ3=0;
C3u3+1L2φ3-φ2+1L3φ3-φ4=0;
C4u4+1L3φ4-φ3=0.
100 және 103 суреттерде көрсетілген электрлік тізбектер қосақталған.

1.2 Электромеханикалық баламаны қолдану және механикалық жүйе баламаларының-электрлік үлгілерін құру
Механикалық жүйе баламаларының электрлік үлгілерін құру үшін механикалық тізбек үғымын енгізген ыңғайлы жэне электрлік және механикалық жүйенің барлық элементтерін екіполюсті түрде қарастыру қажет.
7-кестеде электромеханикалық баламаньщ бірінші жэне екінші жүйесінің электрлік екіполюсі жэне оларға сэйкес механикалық тізбектің екіполюсі келтірілген.
7-кестені пайдаланып, механикалық тізбектің барлық екіполюстерін электромеханикалық баламаның бірінші немесе екінші жүйесіне сэйкес электрлік тізбектің екііюлюстерін тізбектей немесе параллель қосу арқылы алмастырып, механикалық жүйенің электрлік балама - үлгісін математикалық үлгісін түрғызбай-ақ жүзеге асыруға болады
3-кесте

Механикалық жүйені механикалық тізбек түрінде қарастыру аркылы, бірге қозғалатын екіполюстердің полюстерін жалпы түйінге біріктіреді, ал санақ жүйесіне қарағанда қозғалмай қалатын полюстерді жерге немесе қозгалмайтын тірекке қосады.
Мысалы, еркіндік дәрежесі бірге тең механикалық жүйені қарастырайық. Бүл жүйенің механикалық тізбегі 104, б суретте көрсетілген.

9-сурет
3кестені пайдаланып, 9 суретте бүл тізбектің күш-кернеу баламасы бойынша электрлік үлгі - баламасын, ал бұл тізбектің күш - тоқ баламасы бойынша электрлік үлгі - баламасын көрсетеміз.
Екі еркіндік дәрежелі механикалық жүйе, жүйенің механикалық тізбегі көрсетілген. Бүл жүйенің электромеханикалық баламаның бірінші жэне екінші жүйелеріне сэйкес электрлік үлгі-баламасы сәйкесінше көрсетілген.
Механикалық жүйенің механикалық тізбегі мен электрлік үлгі-баламасының құрылымын бұл жүйе щ,т2 жэне тъ үш массадан тұрады. т, массасы катаңдық коэффициенті сх серіппесі мен үйкелісінің тұтқырлық коэффициенті Ьх болатын демифер арқылы қатаң тіреуішке бекітілгеп. тл, т2 және т, массалары өзара қатаңдық коэффициенттері с2 жэне с3 серіппелерімен жэне түтқырлық үйкеліс коэффициенттері Ь2 жэне Ьг болатын демпфер арқылы байланьтсқан тъ массасын P3(t) күші түсірілген.
Механикалық жүйеге сэйкес механикалық тізбек күш-кернеу баламасына сэйкес жүйенің электрлік үлгі-баламасы, жүйенің күш- ток баламасына сәйкес электрлік үлгі-баламасы көрсетілген.

10-сурет
1.3 Электромеханыкалық жүйелер және осы жүйе тербелістерін зерттеуге Лагранж-Максвелл теңдеулерін қолдану
Механикалық тізбектерде және электрлік тізбектерда да тербелмелі процесстер энергияның бір формасынан екіншісіне уақыт өтуімен өзгеру құбылысын білдіреді.
Механикалық және электромагнита энергиялар өзара қайтымды болғандықтан механикалық жэне электромагнитгік жүйелерді электромеханикалық деп аталатын жүйеге біріктіруге болады.
Электромеханикалық жуйенің механикалык бөлігі үшін жалпыланған координаталары болып геометриялық шамалары (орын ауыстыру, бұрыш т.с.с) ал электрлік бөлігі үшін - электрлік шамалар (жиектегі тоқ, түйін потенциалы) алынады. Электромеханикалық жүйелердегі тербелмелі процесстер энергиясының өзгеруі, энергияның сақталуының жалпыланған заңын беретін термодинамикалық бірінші басталуымен сэйкес болады. Сонымен бірге, жүйенің механикалық және электрлік айнымалылары арасында, байланыс теңдеулерімен анықталатын, қандай да бір тэуелділік орындалады.
Электромеханикалық жүйе параметрлері арасындағы тэуелділікті орнату үшін жэне осы жүйе тербелістерінің дифференциалдық теңдеулерін алу үшін Лагранж - Максвелл теңдеулерін қолдану ыңғайлы. Себебі, бул теңдеулер энергетикалық негізді, сондықтан да бұл жүйе параметрлері арасындағы тэуелдділікті орнатуға мүмкіндік береді.
Лагранж- Максвелл теңдеулерін құруға кіріскенде, эдеттегідей, жүйенің еркіндік дэреже санын анықтап, эрі күйінің механикалық жэне электрлік бөліктерінің жалпыланған координаталарыи тацдап алу қажет.
Бұдан кейін, 6- кестеде келтірілген формулаларды қолданып, жүйенің кинетикалық жэне потенциалды энергияларын жүйенің механикалық және электрлік бөліктерінің энергияларының қосындысы ретінде, жэне де жүйенің таралу функциясын механикалық және электрлік бөліктерінің таралу функцияларының крсындысы ретінде анықтау қажет. Соымен бірге, Ньютондық және электрқозғалтушы күштер эсерінен болатын жүмысты ескеріп, жүйеге эсер ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.