Санау жүйелерін оқыту әдістемесі: позициялық жүйелер, түрлендірулер және компьютерлік логика негіздері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:
Санау жүйелері тақырыбын оқыту әдістемесі
Мазмұны
Кіріспе
І. Тарау. Санау жүйелері туралы жалпы түсінік
1. 1. Санау жүйелері туралы түсінік, түрлері . . . 5
1. 2. Сандарды позициялық, ондық санау жүйесіне көшіру . . . 8
1. 3. Позициялық санау жүйелеріндегі арифметикалық амалдар . . . 10
1. 4. Логика негізі және компьютердің логикалық негізі логикалық негізгі түсініктері . . . 11
ІІ. Тарау. Мектеп курсында санау жүйелері тақырыбын оқыту әдістемесі
2. 1. Ақпаратты бір санау жүйесінен басқа санау жүйесіне ауыстыру . . . 15
2. 2. Оқушының ақпараттық мәдениетін анықтау, қалыптастыру, тексеру . . . 24
Қорытынды . . . 29
Пайдаланған әдебиеттер . . . 30
Кіріспе
Тақырыптың өзектілігі
Елбасы Н. А. Назарбаев «Болашақта еңбек етіп, өмір сүретіндер - бүгінгі мектеп оқушылары, мұғалім оларды қалай тәрбиелесе, Қазақстан елінің болашағы да сол деңгейде болады. Сондықтан ұстазға жүктелетін міндет ауыр, » - деген болатын.
Заман талабына сай, мұғалімнен өз пәнін терең білу ғана емес, одан тарихи- танымдық, педагогикалық-психологиялық сауаттылық, ақпараттық білімділік талап етіледі.
Білім беру жүйесін ақпараттандырудың негізгі мақсаты оқушылардың ақпараттық мәдениетін қалыптастыру. Қазақстан Республикасының «Білім туралы» Заңында білім беру жүйесін ақпараттандыру осы саладағы мемлекеттік саясат негізінде анықталып, бұл жүйедегі басты міндеттердің біріне айналып отыр.
Ел Президентінің Қазақстан халқына Жолдауында өткен ғасырдың отызыншы жылдарында сауатсыздықпен күрес жүргізілгендігі, компьютерлік сауаттану жөніндегі ауқымды іске азаматтарды бейімдеу, мемлекеттік қызметке жаңа қызметкерлерді қабылдау кезінде компьютерді, интернетті, электрондық поштаны қолдана білу тәсілдерін талап етеді. Заман ағымына қарай күнделікті сабаққа видео, компьютерді қолдану айтарлықтай нәтиже беруде.
Бұл курстық жұмыста компьютердің логикалық және арифметикалық негіздері турал айтылған. Мектеп оқушыларына санау жүйелері туралы түсінікті қалыптастыру, есептер шығару, кез келген ақпараттың түрлерін сандық ақпаратқа айналдыру жолдары қарастырылған. Санау жүйесіндегі екілік санау жүйесіне, ондық санау жүесіне, сегіздік санау жүесіне және он алтылық санау жүесіне толық тоқталып қарастырылған. Бұл курсытық жұмыс тек оқушылар ғана үшін емс сонымен қатар барлық болашақ мамандар иесіне де арналған. Кез келген мұғалім берілген ақпараттар бойынша кез келген уақытта қолдана отырып, сабағына керекті мәліметтер ала алады
Зерттеудік мақсаты: Оқушыларға компьютердің арифметикалық және логикалық негіздері туралы түсінік бере отырып, санау жүйелеріне есептер шығару жолдарын үйрету.
Зерттеудің міндеті:
- Компьютердің арифметикалық және логикалық негіздерін түсіндіру.
- Санау жүелері туралы түсінік қалыптастыру, есептер шығару әдіс-тәсілдерін түсіндіру.
- Компьютерлік мәдениеті қалыптастыру.
Зерттеудің нысаны: 8 «А» сыныбы
Зерттеу орны: Жамбыл облысы, Талас ауданы, Бостандық ауылы, Алғабас орта мектебі.
Зерттеудің әдісі: Деңгейлік тапсырмалар, есептер шығару, анықтау, қалыпқа келтіру, тексеру.
Зерттеудің негізгі кезеңдері:
- Тақырыпқа байланысты психологиялық, әдістемелік және т. б. ғылыми әдебиеттерді жинақтау, сұрыптау, теориялық талдаулар жасау.
- Педагогикалық тәжірибедегі оқушылардың салауаттылық қабілеттерін дамыту жолдарының әдістемелік негізін ұсыну.
- Іс-әрекеттерге талдау, озық үлгілерін пайдалану және жеке тәжірибедегі үлгілірде ұсыну.
Зерттеудің болжамы: Егер оқушылардың бойында санау жүелері туралы түсінік қалыптастырсақ, онда оқушылар компьюетрдің сандық ақпаратты ғана түсінетіне көзідері жетіп келешекте жақсы компьютерде жұмыс істейтін, аналогтық ақпараттарды сандық ақпараттарға еркін ауыстыра алатын еді.
І. Тарау. Санау жүйелері туралы жалпы түсінік
- Санау жүйелері туралы түсінік, түрлері
Обьектісінің саны туралы мәліметтерді жазу үшін сандар қолданылады. «Сан» түсінігі математика үшін де, информатика үшін де маңызды болып табылады. Сандардың практикалық іс - әрекеттегі маңызды орнына ерекше көңіл аудару үшін пифагоршылар (Пифагордың жолын қуушылар) : «Сан - бұл барлығы», - деген. Сан қандай да бір алфавиттің символымен немесе символдар тізбегімен өрнектеледі. Мұндай символдарды цифр деп атайды. Сан түсінігімен санау жүйелері туралы түсінік байланысты.
Санау жүйелері - сандарды өрнектеудің қандай да бір тәсілі және оған сәйкес сандармен әрекет жасау ережелері.
Бұрынғы және қазіргі қолданылып жүрген барлық санау жүйелері позициялық және позициялық емес санау жүйелері болып үлкен екі топқа бөлінеді. Позициялық санау жүйелерінде цифрдың мәні орналасу орнына тәуелді, ал позициялық емес санау жүйелерінде тәуелді емес.
Позициялық емес санау жүйелері
Адамдар санай бастағаннан бастап оларды жазу қажеттілігі туды. Археологтар алғашқы адамдардың туған жерлерін зерттеу нәтижесінде, олардың заттарды санау үшін қандай да бір белгілерді (таңба, таяқшалар, нүктелер) пайдаланғандарын анықтаған.
Соңынан санауды жеңілдету үшін бұл белгілеулерді үштен, бестен топтап пайдаланған. Мұндай санау жүйелері бірлік деп аталған, себебі кез келген сан бұл жүйеде бірлікті белгілейтін таңбаларды қайталау арқылы құрылған. Бірлік санау жүйелері қазір де кездеседі. Мысалы, курсанттың қай курста оқитынын білу үшін оның жеңіне қанша жолақ тігілгенін санау қажет. Кішкентай балалар қанша жаста екенін айту үшін саусақтарын көрсетеді, ал санау таяқшалары 1 - сынып оқушыларын санауға үйрету үшін қолданылады.
Бірлік жүйе сандарды жазудың ең ыңғайлы әдісі емес. Кейін уақыт өте келе басқа да ыңғайлы санау жүйелері пайда бола бастады. Позициялық емес санау жүйелерін ертедегі мысырлықтар, гректер, римдіктер және басқа да халықтар пайдаланды.
Мысалы, ежелгі мысырлықтар түйінді сандар үшін 1, 10, 100 және т. с. с. арнайы таңбаларды - иероглифтерді пайдаланған. Барлық басқа сандар осы түйінді сандарды қосу арқылы құрылған. Ежелгі мысырлықтардың санау жүйелері ондық, бірақ позициялық емес болып табылады.
Позициялық емес санау жүйелерінде әр цифрдың мәні оның тұрған орнына (позициясына) тәуелді емес.
Мысалы, 3252 санын өрнектеу үшін лотос гүлінің үш талы (үш мың), бүктелген екі пальма жапырағы (екі жүз), бес доға (бес ондық) және екі сырық (екі бірлік) бейнеленген. Санның шамасы оны құратын белгілердің қандай ретпен орналасқанына тәуелді емес, оларды жоғарыдан төмен, оңнан солға немесе кезекпен орналастыруға болады.
Позициялық емес санау жүйелерінің ішінде ең көп тарағаны - римдік санау жүйесі.
Римдік санау жүйесінің негізіне 1 саны үшін І белгісі (бір саусақ), 5 саны үшін V (ашылған алақан) белгісі, 10 саны үшін Х (айқасқан алақандар) белгісі, ал 100, 500 және 1000 сандарын өрнектеу үшінсәйкес латын сөздерінің (centum - жүз, demimille - мыңның жартысы, mille - мың) алғашқы әріптері қолданылады.
Римдік цифрлар
Римдік санды жазу үшін оны мыңдық, жартымыңдық, жүздік, жартыжүздік, ондық, бестік бірліктердің қосындщыларына жіктеген.
Мысалы, 27 санын былай жазған:
XXVII=10+10+5+1+1
Римдіктер аралық сандарды жазу үшін қосу ғана емес, азайту амалын да пайлдаланған. Бұл жағдайда мына ереже қоланылған: үлкен белгінің оң жағына қойылған әрбір кіші белгі санның мәніне қосылады, ал үлкен санның сол жағына қойылған әрбір кіші белгі санның мәніне алынады.
Мысалы, ХІ =10+1, ал IX = 10 - 1
Римдік санау жүйесі бүгінде, негізінен, маңызды тарихи күндерді, кітаптағы томдар, бөлімдер және тарауларды атау үшін қолданылады.
Позициялық емес санау жүйелерінің мынадай кемшіліктері бар: үлкен сандарды жазу үшін әрдайым жаңа таңбаларды енгізіп отыруы қажет;
- бөлшек және теріс таңбалы сандарды өрнектеу мүмкін емес;
- орындау алгоритмі болмағандықтан, арифметикалық амалдарды орындау қиын.
Позициялық санау жүелері
Вавилонда, б. з. д. 2 мың жыл бұрын, адамдар цифрларды басқаша жазған. Алпыстық вавилондық жүйе (яғни, онда алпыс цифр қолданылды) - позициялық принципке негізделген бірінші санау жүйесі. Вавилондық жүйе математика мен астраноммияның дамуына үлкен ықпал еткен, оның ізі осы күнге дейін сақталған. Мысалы, сағатты 60 мин - қа, ал минутты 60 с - қа бөлеміз. Біз вавилондықтар сияқты шеңберді 360 бөлікке (градусқа) бөлеміз.
Позициялық санау жүйелерінде әрбір цифрдың мәні, осы санның жазылуында тұрған орнына (позициясына) тәуелді.
Қазіргі кезде кең тараған позициялық санау жүйелеріне ондық, екілік, сегіздік және он алтылық жүйелер жатады. Санау жүйелерінің атаулары олардың негізіне сәйкес келеді.
Әрбір пазициялық жүйенің нақты анықталған цифрлар алфавиті мен негізі бар.
Позициялық санау жүйесінің негізі цифрлар санына тең және көрші позицияда тұрған бірдей цифрлардың мәндері неше есеге ерекшеленетінін анықтайды.
Сандардың бізге үйреншікті жазылу жүйесі ондық жүйе деп аталады, ол он араб цифрлары
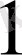 нан тұрады. Кез келген санды жазу үшін 0 - ден 10 - ға дейінгі 10 цифр қолданылады, оның негізі 10 - ға тең; екілік жүйеде тек 0 және 1 цифрларын қолдануға болады, негізі - 2; сегіздік жүйе сегіз цифрдан тұрады, негізі - 8; он алтылық жүйеде ондық санау жүйесінің он цифры және қалған 6 цифрдың орнына латын алфавитінің әріптері қолданылатын, барлығы он алты цифр бар, негізі - 16
нан тұрады. Кез келген санды жазу үшін 0 - ден 10 - ға дейінгі 10 цифр қолданылады, оның негізі 10 - ға тең; екілік жүйеде тек 0 және 1 цифрларын қолдануға болады, негізі - 2; сегіздік жүйе сегіз цифрдан тұрады, негізі - 8; он алтылық жүйеде ондық санау жүйесінің он цифры және қалған 6 цифрдың орнына латын алфавитінің әріптері қолданылатын, барлығы он алты цифр бар, негізі - 16
Позициялық санау жүйелері
Кез келген позициялық санау жүйесінің негізгі құндылығына арифметикалық амалдардың орындалуының қарапайымдылығы мен кез келген санды жазу үшін қажетті символдар санының шектелілігі жатады. Ондық санау жүйесі. Біз онға топтап санауды үйрендік. Он (10
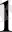 ) жүз (10
) жүз (10
 ), мың (10
), мың (10
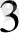 ), миллион (10
), миллион (10
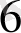 ) сандарын санауға қоллайлы он санының дәрежелері ретінде қабылдаймыз. Санаудың мұндай әдісі мен дөңгелек сандарды қабылдау тарихи қалыптасқан және олар адамның анатомикалық ерекшеліктерімен байланысты. Адамда он саусақ бар, ал ол алғашқы табиғи құрал болғандықтан, 10 саны санаудың негізі ретінде бекіді.
) сандарын санауға қоллайлы он санының дәрежелері ретінде қабылдаймыз. Санаудың мұндай әдісі мен дөңгелек сандарды қабылдау тарихи қалыптасқан және олар адамның анатомикалық ерекшеліктерімен байланысты. Адамда он саусақ бар, ал ол алғашқы табиғи құрал болғандықтан, 10 саны санаудың негізі ретінде бекіді.
Сандарды ондық жүйеде жазу ережелерін толық қарастырайық. Санды жазғанда біз оны санау жүйесінің негізі болатын 10 санының дәрежелерінің қосындысы ретінде өрнектейміз.
Мысалы, 777 саны жеті жүздіктің, жеті ондықтың және жеті бірліктің қосындысын білдіреді.
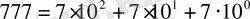
Яғни, бір ғана цифр санның жазылуындағы позициясына қатысты әр түрлі шаманы бейнелейді. Біз санды осылай жазуға үйренгеніміз соншалық, ойша санның цифрлары 10 санының әр түрлі дәрежесіне көбейтіліп, өзара қосылатынын байқамаймыз. Ондық бөлшектерді жазу үшін санның негізі ретінде дәреженің теріс мәні қолданылады. Мысалы, 777, 77 санының жазылуы
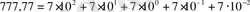
Екілік санау жүйесі . Америкалық ғалым Джон фон Нейман принципі бойынша ЭЕМ арифметикалық есептеулерді екілік санау жүйесінде орындайды, яғни кез келген мәлімет «0» және «1» - ге сәйкес сигналдардың 2 түрлі (магниттелген және магниттелмеген) тізбегімен қолданылады.
Дж. фон Нейман 1946 жылы қазіргі компьютерлердің архитектурасында бүгінге дейін сақталған ЭЕМ архитектурасының принциптерін құрды.
Екілік санау жүйесінің негізі 2 - ге тең, ал жазылуы екі цифрдан (0 және 1) тұрады.
Сандар екілік санау жүйесінде жаймаланған, негізі 2 болатын дәрежеленрдің қосындысы түрінде о немесе 1 коэфиценттерімен жазылады.
Мысалы, екілік санау жүйесінде:
А = 1*2+0*2+0*2+0*2+1*2
Түрінде (жаймасы) жазылғансанның ықшамдалып жазылуы мынадай:
А
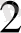
 = 100, 01
= 100, 01

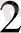
Санның жазылуындағы төменгі индекс, оның қай жүй»еге жататынын көрсетеді. Егер сан қолданылып жүрген ондық санау жүйесінде жазылса, онда төменгі 10 индексі жазылмайды.
Демек, екілік санау жүйесі нөлдер мен бірліктердің тізбегі болып табылады. Мұнымен қатар ол разрядтардың жеткілікті саннын қамтиды.
Екілік санау жүйесінің кемшілігі санды жазудың қолайсыз үлкендігі болып табылады. Мысалы, 277
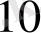
 саны екілік жүйеде былай жазылады:11100011.
саны екілік жүйеде былай жазылады:11100011.
 оған қарағанда сегіздік немесе он алтылық санау жүйелерін қолданған ыңғайлы.
оған қарағанда сегіздік немесе он алтылық санау жүйелерін қолданған ыңғайлы.
Сегіздік санау жүйесі. Сегіздік санау жүйесінің негізі 8 - ге тең, ал 0, 1, 2, 3, 4, 5, 6, 7 сандары алфавиттік сандар болып табылады.
1. 2. Сандарды позициялық, ондық санау жүйесіне көшіру
Екілік, сегізді, он алтылық санау жүйелерінде жазылған сандарды ондық жүйеге түрлендіруді орындау өте жеңіл. Бұл үшін санды жаймаланған түрде жазып, оның мәнін есептеу жеткілікті.
Сандарды екілік жүйеден ондыққа көшіру . Кез келген екілік жүйедегі санды, мысалы, 11, 01 аламыз. Оны жаймаланған түрде жазып, есептеулер жүргіземіз
Сандарды сегіздік жүйеден ондыққа көшіру . Кез келген сегіздік санды, мысалы, 17, 4 аламыз. Оны жаймаланған түрде жазып, есептеулер жүргіземіз:
Сандарды он алтылық жүйеден ондыққа көшіру. Кез келген он алтылық санды, мысалы, 51С аламыз. Оны жаймаланған түрде жазып есептеулер жүргіземіз: ондық жүйеден екілік, сегіздік, он алтылық жүйелерге көшіру. Сандарды ондық жүйеден екілік, сегіздік, он алтылық жүйелерге көшіру күрделілеу және әр түрлі тәсілдермен орындалады. Біз осы сандарды көшіру алгоритмдерінің бірін қарастырайық.
Бүтін санды көшіру алгоритмі
- Ондық санды санау жүйесінің негізіне бөлуіміз керек. Бұл процесс бөлінді бөлгіштен кіші болғанша жалғастырылады.
- Алынған қалдықтарды кері тізбекпен жазамыз.
- ондық жүйедегі 125 санын екілік, сегіздік және он алтылық жүйелерге көшіру мысалын қарастырайық:
Енді ондық бөлшектегі басқа санау жүйелеріне көшіру алгоритмін қарастырайық.
Ондық бөлшекті көшіру алгоритмі
- ондық бөлшек жүйе негізіне тізбектей көбейтіледі, ад алынған бөлшек бөлігі жүйе негізіне тағы да көбейтіледі. Бұл процесс нөлдік бөлшек бөлік алынғанша жалғастырылады.
- алынған бүтін бөліктерді тік бағанға жазамыз 0, 125 ондық санын екілік, сегіздік және он алтылық жүйелерге көшіру мысалын қарастырайық: тік сызық бүтін бөліктерден ажыратады. Сонымен санды екілік санау жүйесінен сегіздік және он алтылық жүйелерге көшіру. Екілік санау жүйесінде берілген санды сегіздікке көшіру үшін оны оңнан солға қарай үш цифрдан топтап бөлген соң, әрбір топты сегіздік цифрға түрлендіреміз. Егер соңғы сол жақтағы топ үш цифрдан аз болса, оны нөлдермен сол жақтан толтыру қажет.
Екілік санау жүйесіндегі 10 санын сегіздік жүйеге көшіру мысалын қарастырамыз:
Көшіруді тезірек орындау үшін екілік санау жүйесіндегі үш цифрдан тұратын топтарды сегіздік цифрларға көшіру кестесін пайдалануға болады.
Екілік санау жүйесіндегі үш цифрлық топтардың сегіздік цифрлармен сәйкестік кестесі
Екілік жүйедегі бүтін санды он алтылық санау жүйесіне көшіру үшін оны оңнан солға қарай топтап, төрт цифрдан бөлу қажет. әрбір топты он алтылық цифрға түрлендіреміз. Егер соңғы сол жақ топтағы цифрлардың саны төрттен аз болса, оны нөлдермен сол жақтан толықтыру қажет.
Екілік жүйедегі 0010111 санын он алтылық жүйеге көшіру: көшіруді тезірек орындау үшін төрт цифрлық екілік топтарды он алтылық цифрларға көшіру кестесін пайдалануға болады.
Екілік санау жүйесіндегі төрт цифрдан тұратын топтардың он алтылық цифрлармен сәйкестік кестесі
Санды сегіздік және он алтылық санау жүйелерінен екілік санау жүйесіне көшіріу. Санды сегіздік және он алтылық санау жүйелерінен екілік санау жүйесіне көшіру үшін санның цифрлары екілік цифрлар тобына түрлендіру қажет. Сегіздік жүйеден екілік жүйеге көшу үшін санның әрбір цифрын екілік санау жүйесіндегі үш цифрдан тұратын топқа, ал он алтылық санды түрлендіруде - төрт цифрлық топқа түрлендіру қажет.
1. 3. Позициялық санау жүйелеріндегі арифметикалық амалдар
Арифметикалық амалдарды екілік санау жүйесінде қарастырайық. Арифметикалық амалдар барлық позициялық санау жүйелерінде бізге таныс ережелермен орындалады. Екілік санау жүйесінің арифметикасы қосу және азайту кестелерін пайдалануға негізделген. Әрбір амалды тиянақты қарастырайық.
Қосу. Екілік жүйеде заңдарды қосу екілік жүйедегі сандарды қосу кестесіәне негізделген. Екілік жүйедегі қосу кестесі өте қарапайым. Тек 1+1 қосу амалын орындағанда ғана жоғарғы разрядқа көшіру орындалады.
Екілік қосу кестесі
0+0=0
0+1=1
1+0=1
1+1=10
Екілік жүйедегі сандарды қосуға бірнеше мысалдар қарастырайық:
1001 1101 1010011, 111
+ + + +
1010 1011 1 11001, 110
10011 11000 1 1101101, 101
Ондық санау жүйесін есептеуге (бірінші мысалға) тексеру жүргіземіз. Ол үшін екілік санау жүйесіндегі санды ондық санау жүйесіне көшіріп, оларды қосамыз. Нәтижелерді салыстыра отырып, қосудың дұрыс орындалғанына көз жеткіземіз.
Азайту . Екілік жүйеде азайту амалын орындау екілік жүйедегі сандарды азайту кестесіне негізделген. Азайту амалын орындау барысында әрдайым абсолют шамасы бойынша үлкенінен кішісі алынып, үлкен санның таңбасы қойылады.
Екілік санау жүйесіндегі азайту кестесі
0 - 0 = 0
0 - 1 = 1
1 - 0 = 1
1 - 1 = 1
Екілік сандарды азайтудың бірнеше мысалдарын қарастырайық:
10111001, 1 110101101
-
10001101, 1 1010
00101100, 0 001001110
1. 4. Логика негізі және компьютердің логикалық негізгі түсініктері
Біздің барлық сөзіміз пікірлерден, яғни сөздік өрнектердің мәндерінен тұрады. Пікірлер табиғи және формалды тілдердің көмегімен өрнектелуі мүмкін. Мысалы, пікір табиғи түрде «бес жердегі бес жиырма бес» сөзімен берілсе, ал формалды (математикалық өрнегі) тілде мына түрде жазылады: «5*5=25».
Пікір деп ақиқат немесе жалған екенін тұжырымдауға болатын, мағынасы бойынша аяқталған сөйлемді айтамыз.
Логика - пікірлер және олардың байланыстары туралы ғылым.
Ойлау, пайымдау әдістері туралы алғашқы ілімдер Ежелгі Шығыс елдерінде пайда болды, бірақ оның негізіне грек ойшылы Аристотель құрған ілім жатады. Неміс ғалымы Г. В. Лейбниц (1666 жылы) алғаш рет ойлау, пайымдау зандарындағы анықталмағандықтың ауызша төрелік етуін және пікірлер арасындағы байланысты математикалық қатынас түрінде анықталатын математика тіліне аударуға тырысты.
Жүз жылдан соң ағылшын математигі Джордж Буль математикалық заңдылықтарға бағынатын логикалық әмбебап тілді құру туралы Лейбниц идеясын дамытты. Ол өз алдына ерекше алгебраны - барлық обьектілерге, атап айтқанда, сандар, әріптерден бастап сөйлемдерге дейін қолдануға болатын белгілеулер мен ережелердің жүйесін ойлап тапты. Джордж Буль логикалық алгебраның атасы болып табылады.
ХХ ғасырдың басына дейін логика іс жүзінде дамыған жоқ, ол тек ЭЕМ теориясының пайда болуынан бастап қана өзінің қарқынды дамуын бастады.
Әрбір ғылым сияқты логика да бірнеше пәндерді қамтиды. Мысалы, формалды логика, математикалық логика ықтималдық логика, диалектикалық логика және т. с. с. пәндерді атауға болады.
Формалды логика сөйлесу тілімен берілген пікірлерді талдаумен байланысты.
Ықтималдық логика кездейсоқ параметрлермен жасалатын сынақтың бірнеше серияларын қолдануға негізделген. Алынған нәтиженің дәлдігі жасалған тәжірибелер санына тәуелді. Мысалы, тиынды лақтырғанда «елтаңба» немесе «жазу» жағының түсу ықтималдығы 1/2-ге тең, яғни тиынды лақтыру саны артқан сайын осы ықтималдық нақтылана түседі.
Математикалық логика дәлелдеулер техникасын зерттейді. Компьютерлер математика пәні сияқты анықтамалар мен дәлелдулерге нақтылықты және қатаң реттілікті талап етеді. Пікірлер алгебрасы математикалық логика аймағы болып табылады.
Пікірлер алгебрасы - идеал пікірлерге қатысты ақиқат немесе жалған пікір деп тұжырымдауға болатын пікірлерді зерттейтін логикалар алгебрасы. Логикалар алгебрасы пікірдің мағынасына назар аударып, терең қарастырмайды.
Сондықтан логикалар алгебрасы тек екі мағынаға ие болады, яғни пікірлердің кез келгені «ақиқат» немесе «жалған» пікірлерінің біреуін ғана сипаттайды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz