Имитатциялық модельдеу имитатциялық модельдеуді ұйымдастыру

1 ИМИТАЦИЯЛЫҚ МОДЕЛЬДЕУ

1.1 Имитациялык модельдеудің кезеңдері
Зерттелетін жүйелер мен объектілердің әр алуан болуына карамастан, оларды имитациялық модельдеу үшін көбінесе мына алты кезеңді бірінен соң бірін орындау қажет:
- мәселені қою;
- математикалық модельдер құру;
- компьютерге арналған программа жасау;
- модельдің түпнұсқаға сәйкестігін бағалау;
- эксперименттердің жоспарын жасау;
- модельдеудің нәтижелерін өңдеу.
Осы кезеңдердің әрқайсысына жеке тоқталайық.

1.2 Мәселені қою

Имитациялық модельдеу, басқа да зерттеу әдістері сияқты, мәселені қоюдан, яғни модельдеудің мақсатын және осы модельдерді құру кезінде ескеретін әр түрлі шектеулерді сипаттаудан басталады.
Имитациялық модельдеудің мақсаты ретінде жауабы ізделіп отырған маңызды сұрақ, әлде тексеруді қажет ететін жорамал немесе ықпалын бағалайтын әсер бола алады.
Мысалы, имитациялық модельдеуді мына сұрақтарға жауап іздеу үшін пайдалануға болады: датчиктерден жауап алатын жаңа алгоритм күрделі қондырғыштардың жұмысына қандай әсер тигізеді немесе оперативті жоспарлаудың нақтылы әдістері өндіріске жұмсалатын қаржыны қанша өнімдейді.Имитациялық модельдеудің мақсаты ретінде, жоғарыда айтылғандай, әр түрлі жорамалдардың ақиқаттығын тексеру де бола алады. Мысалы, кейбір күрделі жүйелердің болашақтағы жағдайы туралы жасалған жорамалды тексеру немесе автобус маршрутының өзгеруі, оның салонының толуын қамтамасыз етеді деген болжамды тексеру, әлде мемлекеттік қорыққа шеттен әкелген тауарлардың жаңа түрі оның экологиялық тепе-теңдігін бұзады деген жорамалдарды тексеру болуы мүмкін. Енді имитациялық модельдеудің мақсаты ретінде әр түрлі әсерлердің ықпалын тексерудің де бір мысалын келтіре кетейік.Металлургиялық пештерде металды қорыту процесінің нәтижесіне, осы пешке үрлеп тұратын ayaғa қосылатын таза оттегінің әсері зор. Сондықтан осы процесті имитациялық модельдеудің мақсаты ретінде байытылған ауадағы оттегі мөлшерінің металл шығымына әсерін анықтау бола алады . Енді осы имитациялық модельдеу кезінде ескеретін шектеулерді

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1. Баженов Л.Б., Гутчин И.Б., Интеллект и машина, изд."Знание", М., 1973.
2. Бердяев Н.А. Человек и машина, Вопросы философии, 1989, N2.
3. Вычислительные машины и мышление. М., "Мир",
4. 5. Кибернетика и философия. АН Латвийской ССР, изд. "Зинатне", 1977.
5. Клаус Г. Кибернетика и философия, М., "Иностранная литература", 1963.
6. 7. Моисеев Н.Н. Компьютеризация, ее социальные последствия, Вопросы философии, 1987, N9.
7. 8. Системно-кибернетические аспекты познания. АН Латв. ССР, изд."Зинатне", 1985.
8. Шалютин С. Искусственный интеллект. М., 1981.
9. Орысша – қазақша сөздік.
10. Ермеков, Ж.Қ

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

Мазмұны

1 Имитатциялық модельдеу имитатциялық модельдеуді
ұйымдастыру ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
1.1 Имитациялык модельдеудің кезеңдері ... ... ... ... ... ... ... ... ... ... ... 3
1.2Мәселені қою ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3
1.3 Матиматикалық модельді құрастыру ... ... ... ... ... ... ... ... ... ... ... .4
1.4 Программа жасау ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5
1.5 Модельдеудің сәйкестігін бағалау ... ... ... ... ... ... ... ... ... ... ... ...5
1.6 Эксперементтерді жоспарлау ... ... ... ... ... ... ... ... ... ... ... ... ... .6
1.7 Модельдеудің нәтижелерін өңдеу ... ... ... ... ... ... ... ... ... ... ... ... ..7
1.8 Модельдеуші алгоритм құру ... ... ... ... ... ... ... ... ... ... ... ... ... ... 7
1.9 Жетекпен өткізу принципі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..9
2.0 Математикалық үміт пен дисперсияның тұрақталған мәнін табуға
қажетті нақтылама саны ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...9
2.1 Чебышев теңсіздігі мына өрнекпен бейнеленеді ... ... ... ... ... ... ...11
2.2 Көпшілікке қызмет көрсету жүйелерін модельдеу ... ... ... ... ... ... .11
2.3 Бірканалды көпшілікке қызмет көрсету жүйесін модельдеу ... ... ... .12
2.4 Жұмысы сенімсіз элемментті көпшілікке қызмет көрсету жүйелерін
модельдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...13
2.5 Салыстырмалы приоритетті көпшілікке қызмет көрсету жүйелерін
модельдеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. ... ..14

1 ИМИТАЦИЯЛЫҚ МОДЕЛЬДЕУ

1.1 Имитациялык модельдеудің кезеңдері
Зерттелетін жүйелер мен объектілердің әр алуан болуына карамастан, оларды
имитациялық модельдеу үшін көбінесе мына алты кезеңді бірінен соң бірін
орындау қажет:
мәселені қою;
математикалық модельдер құру;
компьютерге арналған программа жасау;
модельдің түпнұсқаға сәйкестігін бағалау;
эксперименттердің жоспарын жасау;
модельдеудің нәтижелерін өңдеу.
Осы кезеңдердің әрқайсысына жеке тоқталайық.

1.2 Мәселені қою

Имитациялық модельдеу, басқа да зерттеу әдістері сияқты, мәселені қоюдан,
яғни модельдеудің мақсатын және осы модельдерді құру кезінде ескеретін әр
түрлі шектеулерді сипаттаудан басталады.
Имитациялық модельдеудің мақсаты ретінде жауабы ізделіп отырған маңызды
сұрақ, әлде тексеруді қажет ететін жорамал немесе ықпалын бағалайтын әсер
бола алады.
Мысалы, имитациялық модельдеуді мына сұрақтарға жауап іздеу үшін
пайдалануға болады: датчиктерден жауап алатын жаңа алгоритм күрделі
қондырғыштардың жұмысына қандай әсер тигізеді немесе оперативті
жоспарлаудың нақтылы әдістері өндіріске жұмсалатын қаржыны қанша
өнімдейді.Имитациялық модельдеудің мақсаты ретінде, жоғарыда айтылғандай,
әр түрлі жорамалдардың ақиқаттығын тексеру де бола алады. Мысалы, кейбір
күрделі жүйелердің болашақтағы жағдайы туралы жасалған жорамалды тексеру
немесе автобус маршрутының өзгеруі, оның салонының толуын қамтамасыз етеді
деген болжамды тексеру, әлде мемлекеттік қорыққа шеттен әкелген
тауарлардың жаңа түрі оның экологиялық тепе-теңдігін бұзады деген
жорамалдарды тексеру болуы мүмкін. Енді имитациялық модельдеудің мақсаты
ретінде әр түрлі әсерлердің ықпалын тексерудің де бір мысалын келтіре
кетейік.Металлургиялық пештерде металды қорыту процесінің нәтижесіне, осы
пешке үрлеп тұратын ayaғa қосылатын таза оттегінің әсері зор. Сондықтан
осы процесті имитациялық модельдеудің мақсаты ретінде байытылған ауадағы
оттегі мөлшерінің металл шығымына әсерін анықтау бола алады . Енді осы
имитациялық модельдеу кезінде ескеретін шектеулерді бейнелеу туралы бір-
екі сөз айту қажет. Бұл жұмыс зерттеліп отырған объектінің немесе жүйенің
сипаттамаларын анықтаудан басталады. Осы бағыттағы бірінші қадам қаралып
отырған объект қандай бөлшектерден тұратынын анықтауы керек. Келесі қадам,
осы объектінің елеулі параметрлері мен айнымалыларын айқындау және
солардың мөлшерлеріне қойылатын шектеулерді табу. Үшінші қадамда осы
елеулі параметрлер мен айнымалылардың біріне-бірінің әсерін талдай отырып,
олардың имитациялық модельдеу нәтижесіне ықпалын табу кажет.

1.3 Математикалық модельді құрастыру

Математикалық модель деп, зерттеліп отырған жүйелердегі процестердің
сипаттамалары мен осы жүйелердің елеулі параметрлерінің, бастапқы
шарттарының кіріс айнымалыларының арасындағы байланысты бейнелейтін
қатынастар жинағын айтамыз. Күрделі жүйелерді құрастыратын элементтердің
әртектілігі және олардың неше түрлі кездейсоқ факторлардың әсері ортасында
жұмыс істеуі осы жүйелерді және олардың элементтерін модельдеу үшін әр
түрлі математикалық сұлбаларды колдануға мәжбүр етеді. Солардың ішінен
имитациялық модельдеу кезінде жиі қолданатын келесі сұлбаларды атап кетуге
болады: дифференциалдық және айырымдық тендеулер, марков процестері,
көпшілікке қызмет көрсету жүйелері, динамикалық жүйелер, агрегаттық
жүйелер, ықтималдық автоматтар. Осы сұлбаларды зерттеудің математикалық
әдістерінің жақсы дамығанын ескерсек, оларды күрделі жүйелер элементтерінің
моделі ретінде пайдалануға болатынын дәлелдеу керек жоқ . Сондықтан бүл
сұлбалар имитациялық модельдеу әдісінің үлгілі сұлбалары деп аталады .
Математикалық модельдерді құрастыру кезінде назарға ұстайтын тағы бір
мәселе бар. Ол ешқандай математикалық модельдің зерттеліп отырған
процестерге дәл сәйкес бола алмайтыны, тек қана осы процестердің, алға
қойылған мәселелерге тән, ең елеулі сипаттамаларын бейнелей алатындығын
ұмытпау керек. Осыған байланысты математикалық модель қаншама күрделі болуы
қажет деген сұрақ туады. Бір жағынан қарағанда, іс жүзінде кездесетін
жүйелер өте күрделі, сондықтан оларды бейнелейтін модельдер де күрделі
болуы керек деген тұжырымға келуге болады. Бірақ бұл тұжырымның
дұрыстығының шегі болуы қажет. Себебі өте күрделі модельдерді құрастыру
мүмкін болғанмен, оларды пайдалану өте көп уақыт алады және осы модельдерді
бейнелейтін күрделі математикалық қатынастарды шешкен кезде көптеген
қателер жіберіледі де, алынған нәтижелердің пайдасы жоққа шығады. Сондықтан
жылдам жүзеге асырылатын және алға қойылған мәселелерді зерттеуге
жеткілікті дәлдікпен сипатталатын модельдерді кұрастыру қажет. Тағы бір
ескеретін жәй, күрделі жүйелерді имитациялық модельдеу кезінде олардың
математикалық моделін түрлендіру арқылы зерттеліп отырған процестердің әр
қадамын бірінен соң бірін бейнелеп отыратын модельдеуші алгоритм кұру
керек. Бұл алгоритм карастырылып отырған процестердің логикалық кұрылымы,
хал-күйі және кұрамы туралы ақпаратты сақтауы тиіс.

1.4 Программа жасау

Имитациялық модельдеудің бұл кезеңінде зерттеушінің алдында оны қай
алгоритмдік тілде жазу керек деген сұрақ туады. Соңғы жылдары компьютермен
модельдеудің тез дамуына байланысты имитациялық модельдеуге арналып
жасалған көптеген алгоритмдік тілдер пайда болды. Бірақ осы тілдердің
көбісі белгілі бір математикалық сұлбамен бейнеленген обьектілерді
модельдеуге ғана бағытталған. Мысалы, GPSS деген тіл көпшілікке қызмет
көрсету жүйелерінің жұмысын модельдеуге бейімделсе, SlMULA тілі арнайы көп
мөлшерлі теңдеулермен бейнеленетін экономика жүйелерін имитациялауға
арналған. Универсалды тілдерге қарағанда бұл арнайы тілдердің программасын
тезірек кұрастыруға болады және осы арнайы имитациялық тілдердің құрамында
программаны құрастырғанда жіберілетін қателерді тез табу амалдары
ескерілген . Дегенмен, имитациялық модельдеу кезінде универсалды тілдер де
(Паскаль, Си, Фортран, Бейсик) жиі қолданылады. Бұл тілдердің де
имитациялық модельдеуге тиімді біраз қасиеттері бар. Мысалы, біраз күрделі
жүйелерді (автоматтандырылған басқару жүйелерін, ақпаратты іздеу
жүйелерін) модельдеген кезде осы модельдеуден алған нәтижелерді көрсету
түрінің мағынасы зор. Ал программа арқылы алынған нәтижелерді әр түрлі
сұлбада басып шығару тәсілдеріне универсалды тілдер өте бай келеді.
Сондықтан зерттеушінің алдында программалау тілін таңдау мәселесі тұра
қалса, ол өзі жақсы меңгеретін тілге тоқтауы дұрыс деп есептейміз. Қанша
тиімді болғанымен, өзін дұрыс игермеген тілді пайдаланғанша, білетін
программалау тілін қолдану тез де және сенімді де болады.

1.5 Модельдеудің сәйкестігін бағалау

Өте күрделі жүйелерді зерттегенде кездесетін проблемалардын бірі, ол бұл
жүйелердің модельдерінің қандай болмасын, осы жүйеге тән процестерді толық
сипаттай алмайтындығы. Сондықтан жақсы модель деп, осы жүйедегі
өзгерістердің, оның негізгі көрсеткіштеріне әсерін дұрыс білдіретін
модельдерді айтады . Алынған модельмен осы модель бейнелейтін процестердің
сәйкестігін тексеру әлде, басқаша айтқанда, кұрастырылған модельді бағалау
қажет.
Математикалық модедьдерді бағалау көбінесе үш сатыдан тұрады.
Бірінші сатыда зерттелетін процесс пен оның моделінің тұрпайы сәйкестігі
тексеріледі. Тұрпайы модель мынандай сұраққа болымды жауап беруі керек.
Егер осы модельге, қарастырылып отырған жүйенің маңызды параметрлері мен
айнымалыларының шектік мағыналарын қойғанда, абсурдты нәтижелерге әкеліп
соқпай ма?
Тексерудің екінші сатысында модель жасау алдындағы бастапқы болжамдарды
тексеру керек. Яғни, модельденетін жүйенің қандай параметрлері мен
айнымалыларын маңызды деуге болады және құрылған модельде елеулі
параметрлердің бәрі ескерілген бе?
Елеулі айнымаларды анықтау үшін, олардың жүйе жұмысының баламасына әсерін
білу кажет. Ал модельде барлық елеулі параметрлер мен айнымалылардың
қамтылғанын анықтау үшін статистикалық анализ әдістерін, мысалы, тиімділік
көрсеткішінің дисперсиясын пайдалануға болады.
Модельдің сәйкестігін бағалаудың үшінші сатысында жүйенің кіріс
айнымалыларын түрлендіру тәсілдері тексеріледі. Осындай тексерудің негізі
ретінде дисперсиялық, регрессиялық, факторлық, спектральдық талдаулар,
автокорреляция, келісім баламасымен тексеру, статистикалық тандамалардың
математикалық үміті мен дисперсиясын бағалау әдістері қолданылады.
Жасалған модельдерді бағалағанда, олардың іс жүзінде қолданушыларға
қолайлылығын естен шығармау кажет. Осы айтылған жағдайларды қорыта келіп,
жасалған модельді жақсы модель деп санау үшін ол:
- іс жүзінде қолданушыға қолайлы және анық;
- басқаруға жеңіл;
- ол арқылы алынған нәтижелер дұрыс және толық;
- жаңа талаптар бойынша өзгертулер енгізуге бейімделген болуы қажет екенін
анықтаймыз.

1.6 Эксперименттерді жоспарлау

Жасалған модельдің зерттелетін жүйеге немесе объектіге сәйкес екенін
дәлелдегеннен кейін оны имитациялық модельдеуге кірісу керек. Яғни
зерттеліп отырған объектінің берілген уақыт аралығындағы жұмысын, осы
мерзімнің басынан аяғына дейін бейнелеп шығу қажет. Осындай бейнелеуді
келешекте имитациялық модельдеудің бір нақтыламасы деп атаймыз.
Осы бір нақтыламаның арқасында анықталған корсеткіштердің мәні, әрине,
қарастырылып отырған объектілердегі процестің объективті сипаттамасы бола
алмайды. Себебі имитациялық моделъдеу әдісі, іс жүзінде кездесетін әр
түрлі (станоктың сынып қалуы, жұмысшының жұмысқа кешігуі, шикізаттың
жетіспеуі және т.б.) кездейсоқтықтардың бұл процеске әсерін бейнелей
алатындығынан, осы көрсеткіштердің мәні де кездейсоқ шама болады.
Сондықтан имитациялық модельдеудің нәтижесінде анықталатын көрсеткіштердің
мағынасын бірнеше нақтыламалардың орта мәні ретінде ғана қарастыру керек.
Егер осы нақтыламалардың санын (n) жеткілікті мөлшерде тағайындасақ, үлкен
сандар заңына сәйкес, керсеткіштің мағынасы тұрақты болып, оның іс
жүзіндегі мәнін дәлірек сипаттайды. Кейде имитациялық модельдеудің бір
нақтыламасының нәтижесі де дәл сипаттама бере алады. Ол үшін модельденіп
отырған объектідегі процестер эргодикалық касиетке ие болуы керек.

1.7 Модельдеудің нәтижелерін өндеу

Имитациялық модельдеу нақтыламаларын жузеге асырғаннан кейін оның
нәтижелерін өңдеу қажет. Жоғарыда айтылғандай имитациялық модельдеу
көбінесе өте күрделі жүйелерді зерттеуге қолданылады және модельдеу
кезінде бір емес, бірнеше нақтыламалар алынады. Сондықтан осы жүйелердегі
процестерді толық сипаттау үшін модельдеу барысында көптеген параметрлер
мен айнымалылардың мағынасын қадағалап компьютердің жадында ұстау қажет.
Ал осы көп деректерді өңдеу үшін біраз уақыт және күш салу керек. Өте
күрделі жүйелерді модельдегенде осынша деректермен жұмыс істеу қазіргі
компьютерлердің де қольнан келмейтіні анық. Сондықтан имитациялық
модельдеу барысында осы көп деректерді компьютердің жадында сақтау және
өңдеу әдістерінің біраз ерекшеліктері болуы тиіс. Ең басты ерекшелік -
имитациялық модельдеудің нәтижелері ең аяғында ғана емес, осы модельдеудің
басынан бастап біртіндеп анықтала бастауы керек және әр көрсеткіш
компьютердің жадының бір ғана бөлшегін алып, оның жаңа мәні бұрынғы
мөлшерін түрлендіру арқылы қайтадан осы бөлшекте сақталуы тиісті.
Имитациялық модельдеу кезінде көптеген кездейсоқтықтардың әсерін
ескергендіктен, оның біраз көрсеткіштері де кездейсоқ шамалармен
бейнеленуі мүмкін. Сондықтан осы кездейсоқ шамалардың мағынасы ретінде
матиматикалық үміттер, дисперсиялар және тағы басқа ықтималдылық
сипаттамалары қолданылады. Осы алты саты, әрине, жалғыз имитациялық
модельдеу кезінде ғана емес, басқа да зерттеулерде кездеседі. Алайда,
имитациялық модельдеудің кейбір сатылары басқа зерттеулердің осындай
сатыларынан біраз айырмашылығымен танылады. Осындай сатыларға
математикалық модель құру, эксперименттерді жоспарлау және оның
нәтижелерін өндеу сатылары жатады. Сондықтан имитациялық модельдеудің осы
айырмашылықтарымен танысуды математикалық модель құру сатысының ең басты,
яғни бұл модельдерді түрлендіру арқылы модельдеуші алгоритмдерді кұру
ерекшелігінен бастайық.

1.8 Модельдеуші алгоритм құру принциптері

Күрделі жүйелерді имитациялық модельдеу кезінде оның математикалық моделін
түрлендіру арқылы модельдеуші алгоритм құрылады. Содан кейін осы алгоритм,
қарастырылып отырған процестердің әр қадамын компьютер арқылы қадағалап
бейнелеуге, яғни имитациялауға қолданылады. Имитациялау барысында осы
процесті сипаттайтын ақпараттың логикалық кұрылымы, түрі мен құрамы және
түрлену мезгіл тізбегі бұзылмауы қажет.
Енді осы модельдеуші алгоритмдерді құрудың негізгі принциптерімен
танысайық.
t принципі
Күрделі жүйелердің жұмыс барысын бейнелеу үшін мынадай сипаттамаларды
қолданайық
Z(t)={ Z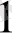(t),Z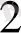(t),...,Z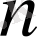(t)
Сонда, осы жүйелерде өтіп жатқан процестерді модельдеу үшін Z(t)
функциясын табу қажет және осы функция бойынша керекті көрсеткіштердің
мөлшерлерін есептеу керек. Ол үшін, ең бірінші, математикалық модельдің
қатынастарын Z() (t болсын) функциясы бойынша Z{t+t}
анықтауға ыңғайландырып түрлендіру керек. Детерминді процестерде Z(t)
функциясының t0,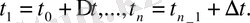. мезгілдердегі мәндерін рекуррентті қатынастар
арқылы табуға болады. Яғни 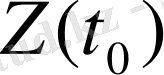бойынша 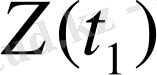функциясын, 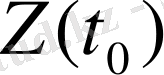және
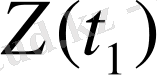бойынша 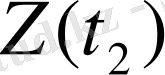функциясын табуға, ал жалпы алғанда

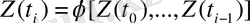
тәуелділігін қолдануға болады.
Кездейсоқ (стохастикалық) процестерді сипаттаудың сәл өзгешелігі бар. Бұл
жағдайда процестердің 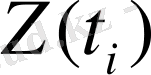сипаттамалары тікелей тәуелділігінен
табылмайды. Бұл тәуелділік тек қана осы 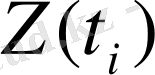кездейсоқ функциясының
үлестірім заңын анықтайды. Содан кейін осы заңға сәйкес кездейсоқ
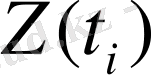функциясының бір мәні алынады. Осындай операцияны бірнеше рет қайталап,
модельденіп отырған процестің [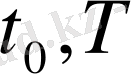] аралығындағы бір нақтыламасын
бейнелеуге болады.
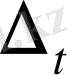принципі іс жүзінде кездесетін әр түрлі жүйелерді қамтитын көптеген
модельдеуші алгоритмдерді кұрастыруға негіз бола алатын уииверсалды
принцип. Алайда, бұл принцип компьютерді қолданғанда ең көп есептеуді
талап етеді.
Ерекше жағдай принципі
Әр түрлі күрделі жүйелерді зерттегенде олардың көбінесе екі күйде болатыны
анық байқалады: әдеттегі және ерекше күйлері. Жүйе көбінесе әдеттегі
күйінде болады, тек қана оған сырттан жаңа ақпарат, әлде әр түрлі әсер
келіп түссе немесе осы жүйенің кейбір көрсеткіштері өзінің шектік
мәндерінен асып кетсе, аз уакыт аралығында бұл жүйе ерекше күйде болады.
Осы ерекше жағдайға сәйкес уақыт мезгілдерінде жүйелерді бейнелейтін
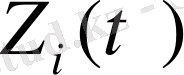функциялары өздерінің мәнін күрт өзгертеді. Сондықтан зерттеліп отырған
жүйелердің әр түрлі қасиеттері осы ерекше жағдай кезінде мәліметтермен
айқындалуы тиіс.
Осындай қасиеттермен сипатталатын жүйелердің модельдеуші алгоритмдерін
кұрастыру ерекше жағдай принципіне негізделген.
Осы принципті қолдану үшін, ең бірінші, математикалык модельдің
қатынастарын, бір әлде бірнеше бұрынғы ерекше жағдайлар арқылы жаңа ерекше
жағдайды табуға икемдей түрлендіру керек. Екіншіден, бұл принципті
пайдаланғанда ерекше жағдай туатын уақыт мезгілдерін алдын-ала анықтау
қажет. Сондықтан бұл принципті колданғанда принципі сияқты
алгоритмінің бос жүрісі болмайды.

1.9 Жетекпен өткізу принципі

Бұл принцип көбінесе көпшілікке қызмет көрсету жүйелерін модельдегенде
колданылады. Оның негізі жүйеге келіп түскен әрбір өтінішті басынан бастап
қызмет көрсетіп болғанша бақылап отыру болады. Яғни әрбір өтініштің қызмет
керсетудің барлық сатыларынан біртіндеп өтуі камтамасыз етіледі.
Басында ол кезекке тұруы немесе қызмет көрсетуге алынуы мүмкін. Қызмет
керсететін прибор жұмыстан шығып қалса, өтініш оның жөндеуден шығуын тосу
және тағы басқа кезеңдерден өтуі қажет. Яғни бұл өтінішке қызмет
көрсетіліп болғанша немесе әрі қарай қызмет көрсете алмайтын жағдайға
кездескенше таса болмауы тиіс.
"Жетектеп өткізу" принципі өте тиімді модельдеуші алгоритмдер құрастыруға
мүмкіншілік береді, бірақ олардың логикалық құрылымы өте күрделі және
кейде шиеленісті болуы мүмкін.
Айтып кететін тағы бір жәй, іс жүзінде модельдеуші алгоритмдерді
құрастырғанда бірнеше принцип қатар қолданылуы да мүмкін. Мысалы,
модельдеуші алгоритмнің жалпы құрылымы "ерекше жағдай" принципіне
негізделсе, ал осы ерекше жағдайлардың аралығында "жетектеп өткізу"
принципі тиімдірек болуы мүмкін.
Модельдеуші алгоритмнің жалпы құрылымы
Модельдеуші алгоритмнің жалпы кұрылымы имитациялық модельдеудің негізгі
мақсатын, яғни зерттелетін жүйенің жұмысын немесе маңызды көрсеткіштерін
жақсартуға себепкер болуы қажет. Ал осы мақсатты жүзеге асыру үшін, ең
бірінші қарастырылып отырған обьект әлде жүйедегі процестердің белгіленген
уақыт аралығындағы хал-күйін модельдей білу керек. Екіншіден, модельдеу
кезінде алынған көрсеткіштердің ақиқаттығын және дәлдігін қамтамасыз ету
қажет. Үшіншіден, модельдеу арқасында, зерттеліп отырған объектінің
жұмысын жақсарту бағыттарын айқындау керек. Ең кіші цикл зерттелетін
жүйенің жұмысын берілген уақыт аралығында модельдейді. Имитациялық
модельдің осы уақыт аралығындағы жұмысын болашақта модельдеудің бір
нақтыламасы деп атаймыз.Осы керсеткіштердің дұрыс мағынасын табуға қажетті
нақтыламалардың санын (N) немесе осы көрсеткіштердің алдын-ала
тағайындалған дәлдігін пайдалануға болады.

2 МАТЕМАТИКАЛЫҚ ҮМІТ ПӘН ДИСПЕРСИЯНЫҢ ТҰРАҚТАЛҒАН МӘНІН ТАБУҒА қажетті
нақтылама саны
Математикалық үміттің мәнін анықтау үшін іс жүзінде арифметикалық орташа
қолданылатыны белгілі

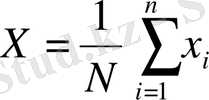
Осы формуламен табылған арифметикалық орташа мына тәуелділікке
қайшы келмеуі керек

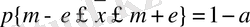
математикалық үміті т, дисперсиясы 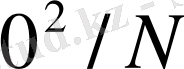, калыпты үлестірім заңына
ұқсас екендігі анық. Сондықтан осы көрсеткішті бағалау дәлдігі үшін мына
теңдікті келтіре аламыз

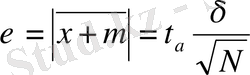
Яғни

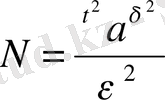
Бұл формуладағы a2 - арифметикалық орташаның дисперсиясы. Осы дисперсияның
мөлшері белгісіз болғандықтан, оның орнына

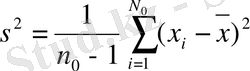
формуласымен есептелетін дисперсияның жуық шамасы алынады.
Енді әр түрлі көрсеткіштердің дисперсиясын керекті дәлдікпен, яғни

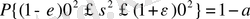
тәуелділігімен бағалауға мүмкіндік беретін N нақтыламасын анықтайық.
Дәлділіктің мөлшері, әрине, 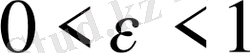аралығында болуы тиіс.
Бұл жолы да дисперсияның бағасы ретінде колданылатын 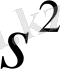шамасының,
математикалық үміті мен дисперсиясы

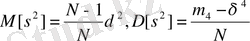
тең, қалыпты заңмен сипатталатынын ескере отырып, көрсеткіштің дәлдігін
мына теңдікпен бейнелейміз:

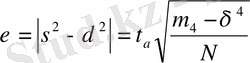
Осы өрнектен, белгілі үш сигма кағидасын ескере отырып, нақтылама санын
еселейтін формуланы шығаруға болады:

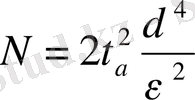
Белгісіз а бұл жерде де жоғарыда айтылған тәсілмен табылады.
Нақтылама санын анықтауға Чебышев теңсіздігін қолдану
Бұған дейін нақтыламалар санын анықтау үшін біз имитациялық модельдеу
кезінде пайдаланатын көрсеткіштер қалыпты үлестірім заңына бағынышты деп
есептедік. Енді бұл болжамнан бас тартайық, яғни көрсеткіштер басқа да
үлестірім заңдарымен сипаттала алатын болсын.
Осы жағдайда нақтылама санын табу үшін Чебышев теңсіздігін қолдануға
болатынын көрсетейік.

2.1 Чебышев теңсіздігі мына өрнекпен бейнеленеді:

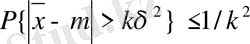
Бұл өрнек кез-келген көрсеткіштің арифметикалық орташасы мен математикалық
үмітінің айырмашылығы 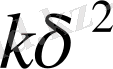мөлшерінен асып түсу ықтималдылығы
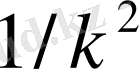санынан аспайтындығын көрсетеді.
Мысал [4]. Имитациялық модельдеу нәтижесінде алынатын х шамасы 0,95
ықтималдылығымен м ±4 аралығында жатуын қамтамасыз ету керек
болсын. Яғни мына теңсіздік

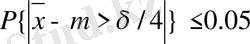
орындалуы тиіс. Ол үшін 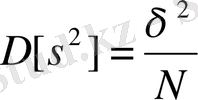екенін ескере отырып, Чебышев теңсіздігін
жазайық:

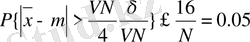
Яғни N = 320.
Табылған нақтылама саны, қалыпты үлестірім заңы қолданғанда қажетті саннан
көбірек болатынын ескеру керек.

2.2 Көпшілікке қызмет көрсету жүйелерін модельдеу

Іс жүзінде кездесетін әр түрлі күрделі жүйелерді зерттегенде, оларды
көпшілікке қызмет көрсету жүйелері (КККЖ) ретінде қарастыруға болады.
Өкінішке орай, көпшілікке қызмет көрсету теориясының математикалық
аппаратының долдану мүмкіншілігі өте шектеулі. Бұл аппарат тек қана
кірісіндегі талаптар қарапайым ағынын құратын, ал осы талаптарға қызмет
көрсету уақыты экспоненциалдық үлестірім заңымен бейнеленетін жүйелерді
ғана зерттей алады. Сондықтан көпшілікке қызмет көрсету жүйелерінің
сұлбасына келтіріле алатын көптеген күрделі жүйелерді зерттеу үшін
имитациялық модельдеу әдісі қолданылады.
Енді көпшілікке қызмет көрсету жүйелерін имитациялық модельдеу әдісімен
танысуды ең қарапайым бірканалды КҚКЖ -н модельдеуден бастайық.

2.3 Бірканалды көпшілікке қызмет көрсету жүйесін модельдеу

Осы жүйенің кірісіндегі талаптар Пальм кездейсоқ оқиғалар ағынын құратын
болсын және ол ағынның оқиғаларының аралық мәнінің үлестірім заңы
берілсін.
Бұл талаптар қызмет көрсету каналының алдына кезекке тұрып, әрқайсысы өз
кезегіне сәйкес бірінен соң бірі қызмет көрсетілуге алынсын.
Кезекте тұру мерзімі шектелулі дел есептейік. Жалпы жағдайда, бұл мерзім
үлестірім заңы белгілі кез-келген кездейсоқ шама бола алады. Талаптарға
қызмет көрсету мерзімі де үлестірім заңы белгілі кездейсоқ шама болсын.
Осы көпшілікке қызмет көрсету жүйесінің [O,T] аралығындағы жұмыс барысын
модельдейік. Демек, қызмет көрсетілуге 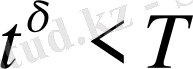уақытында алынған талаптан
каналдын босау мезгілі 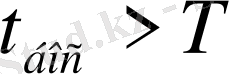теңсіздігімен сипатталса, ол талапқа кызмет
көрсетілмеуі тиіс.

1- ші оператордың көмегімен имитациялық модельдеуге қажетті бастапкы
деректер, яғни талаптар ағынының параметрлері, берілген үлестірім
заңдарырының сипаттамалары, модельдеу мерзімі және тағы басқалар
тағайындалады.
2 - ші оператор имитациялық модельдеудің неше рет қайталанғанын, яғни
нақтыламалар санын, есептейді.
- ші оператор жаңа нақтыламаны модельдей бастауға даярлық жасайды.
- ші және 5 - ші операторлардың көмегімен кезекті талаптың жүйеге келіп
түскен мезгілі
Табылады . Бұл формуладағы алдыңғы талаптың келіп түскен мезгілі, ал
- осы екі талаптың аралығы.
6 - шы оператордың көмегімен , j-шы талаптың келу уакыты модельдеу
интервалына ене ме, әлде енбей ме деген сұраққа жауап алынады, яғни шарты
тексеріледі. Осы шарт [0.T] интервалы толық модельденіп болғанда ғана
орындалмайтыны анық. Сондықтан болған жағдайда 6 - шы
оператордан тікелей 24-операторға өтіп, имитациялық модельдеудің бір
нақтыламасының нәтижелерін есептеу қажет.
Ал (10.1) шарты орьшдалған жағдайда 7-ші оператор келіп түскен талаптардың
санын өзгертеді.
8 - ші оператор кезекті талаптың келген уақытында кызмет көрсетуші
каналдың бостығын тексереді. Канал бос емес, яғни жағдайында бұл
талап кезекке койылады. Сондықтан 9 –шы оператор кезекте тұрған
талаптардың m санының жаңа мөлшерін есептейді және каналдың осы талапты
күтпегенін деп белгілейді.
10 - шы және 11 - ші операторлар осы талалтың кезекте кай мезгіліне дейін
тұра алатнын анықтайды:

2.4 Жұмысы сенімсіз элементті көпшілікке қызмет көрсету жүйелерін
модельдеу

Көпшілікке қызмет көрсету сұлбасымен бейнеленетін бірсыпыра нақтылы
жүйелерді зерттегенде, олардың қызмет көрсету каналдарының сенімсіздігін,
яғни анда-санда істен шығып қалатынын ескеру қажет.
Жоғарыда қаралған бірканалды көпшілікке қызмет көрсету жүйесін сенімсіздік
қасиетімен толықтырайық. Яғни, каналдың бұзылмай қызмет істеу уақыты
үлестірім заңы белгілі кездейсоқ шама болсын. Істен шығып қалған каналды
қалпына келтіру уақыты да әдетте үздіксіз кездейсоқ шама болатыны анық.
Бұл шаманың да үлестірім заңы белгілі деп есептейік. Егер канал кезекті
талапқа қызмет көрсетіп жатқан кезде бұзылса, ол талапқа қайтадан қызмет
кәрсетілмейді.
Енді каналдың істен шығып қалу мүмкіншілігін ескере алатын ішене
алгоритмді кұрастырайық .
Бұл шарт орындалмаған, яғни каналдын сенімсіздік сипаттамасы ескерілмеген
жағдайда, кезек негізгі алгоритмнің 22 - ші операторына тиеді. Сондықтан
ұсынылып отырған ішене алгоритм іске аспай қалады.
Ал R=1 шарты орындалған жағдайда көпшілікке қызмет көрсету жүйесі
каналының сенімсіздік сипаттамасын ескере отырып модельденеді. Сондықтан
21-ші оператордан кейін, осы ішене алгоритмнің 1-ші операторында L= 0
шарты тексеріледі.
Бұл шарттың мағынасы мынада. Қызмет көрсетуші каналдың жұмысын модельдеген
кезде ең маңызды дерек каналдың істен шығу мезгілі (tіш). Сондықтан кез-
келген уақыт үшін осы мезгіл алдын-ала модельденіп отыруы керек. Соны
қамтамасыз ету үшін L белгісін кіргізейік:

Егер каналдың істен шығу мезгілі ,анық талса ,анықталған.
өткен істен шығу мерзімі қолданылып,келесі істен шығу
- мезгілін табу қажет боолса.
Ең бастапқы шақта, әрине, L =О шарты орындалады да 2 мен 3-ші операторлар
каналдың бұзылмай жұмыс істеу мерзімін болжай отырып, келесі істен шығатын
мезгілін анықтайды. Сондықтан 3 -ші оператор L белгісінің мәнін
өзгертеді.
Ал бірінші оператордың шарты орындалмаған жағдайда кезек бірден 5 - ші
операторға беріледі. Ол осы ішене алгоритмнің ең маңызды шартын, яғни
кезекті талапқа қызмет аяғына дейін көрсетілуін, тексереді
Бұл шарт орындалған жағдайда кезекті талапқа қызмет көрсетілді деген
мәлімет негізгі модельдеуші алгоритмнің 22 - ші операторында санаққа
тіркеледі. Ал бұл шарт орындалмаса, канал кезекті талапқа қызмет көрсетіп
жатқан уақытында бұзылғаны мәлім болады да, бұл талап осы жүйеден толық
қызмет ала алмай кетуіне тура келеді.
Сондықтан 6 және 7 - ші операторлар каналды қайта қалпына келтіру мерзімін
модельдеп, келесі талапты қабылдауға даяр () мезгілін анықтайды.
Келесі 8 - ші оператор, каналды қалпына келтіру мерзімі модельдеу
интервалына кіре ме, кірмей ме деген сұраққа жауап береді. Осы оператордың
шарты орындалған жағдайда, 9, 10, 11-ші операторлардың көмегімен бірнеше
керсеткіштерді анықтай отырып, кезек 12 - ші операторға беріледі. Бұл
оператор каналды қалпына келтіруге жұмсалған уақыттың жаппы мөлшерін
есептеуге бейімделген.13-ші оператор арқылы каналдың қалпына келген
мезгіліне бұл канал бос деген сипаттама беріледі. Ал 14 - ші оператор
каналдың келесі істен шығатын мегілін жобалау үшін дайындық жасай
бастайды, және осы ішене алгоритмнің соңғы операторы болады. Енді кезек
негізгі модельдеуші алгоритмнің 23 -ші операторына беріледі.

2.5 Салыстырмалы приоритетті көпшілікке қызмет көрсету жүйелерін
модельдеу

Кірісінде бүрынғыдай бір ғана емес, бірнеше талаптар ағыны бар көп
каналды көпшілікке қызмет көрсету жүйелерін қарастырайық. Осы
ағындардың саны болсын және олардың әрқайсысы өзінің кездейсоқ
заңдылығымен сипатталсын. Бұл ағындардың әрқайсының маныздылығы да бір-
бірінен өзгеше болсын. Дәлірек айтқанда, q - номерлі ағынның талабы q+l -
номерлі ағынның талабынан маңызы жоғары болсын. Сол сияқты, q+l ағынньщ
талабы q+2 - ші ағынның талабынан жоғары болсын.
Ал бір ағынның ішіндегі талаптардың маңыздылығы біріне-бірі пара-пар деп
есептейік.
Осы жүйе келіп түскен талаптарды қызмет көрсетуге тек
маңыздылығына сәйкес қабылдайды. Яғни кезекте тұрған талаптардың ішінен
қызмет көрсетуге әрдайым ең маңызды ағьшның талабы ғана алынады. Бірақ
қызмет көрсетуге алынған талапқа, оның маңыздылығының мәніне қарамай және
осы мезгілде одан маңыздырақ талаптардың келуіне қарамай, толық қызмет
көрсетіледі. Бұл салыстырмалы приоритетке тән тәртіп екені мәлім.
Салыстырмалы приоритетті көпшілікке қызмет көрсету жүйелерінің модельдеуші
алгоритмінің құрылымы жоғарыда қаралған жүйелерден көп өзгеше болады. Оның
үш себебі бар. Біріншіден, бұл құрылым бір емес, бірнеше кездейсоқ ағынды
модельдеуге және соншама кезек үйымдастыруға икемделген болуы қажет.
Екіншіден, салыстырмалы приоритетке сәйкес қызмет көрсетуге алу ережесінің
күрделігін ескеру керек. Ал үшіншіден, имитациялық модельдеудің нәтижесін
шығарғанда маңыздылығы әртүрлі талап ағындарына сәйкес көрсеткіштерді жеке
қарастыруды қамтамасыз етуі қажет.
Осы айтылған ерекшеліктерді дұрыс жүзеге асыру үшін мына әдістермен
танысайық.
Ең бірінші, талаптар кезектерін модельдеу әдістерін қарастырайық.
Модельдеуші алгоритмнің жұмысы тиімді болу үшін имитациялық модельдеудің
бастапқы кезінде барлық Q кезектерде кем дегенде бір бірден талап болуын
қамтамасыз ету кажет. Ол үшін осы жүйенің модельдеуші алгоритмінін
сүлбасын әрбір кезекке бір талап қою әдісін [30] іске асыратын
операторлардан бастау керек. Ал осыдан кейін кезектегі бос орынды
толтыру әдісіне көшкен жөн болады.
Осы екі әдістің керегін колдану үшін L белгісін енгізейік:

Егер талаптар кезегінің оқиғалары модельдеуге әрбір кезекке бір талап
қою әдісі қолданылса ;
Егер талаптар кезегінің оқиғаларын модельдеуге кезекті бос орынды толтыру
әдісі қолданылса .
Бұл белгінің бастапқы мәні L=1 екені анық.
Енді қарастырылып отырған жүйе көп каналды болғандықтан осы каналдарды
жүмысқа қосу тәртібіне көңіл аудару жөн. Бұл тәртіп имитациялық
модельдеудің бас кезеңдерінде бір ережеге, ал басқа кезеңдерде екінші
ережеге бағынышты болатыны анық. Себебі бастапқы кезде барлық каналдардың
бірінен соң бірінін жұмысқа қатысуын қамтамасыз ету керек. Ал осыдан кейін
бірінші босаған канал жаңа жұмысқа алғашқы болып кірісуі қажет. Осы екі
ережені дұрыс қолдану үшін ф белгісін енгізейік:

eгep жұмысқа кіріспеген каналдар әлі бар болса;
егер каналдардың әрқайсысы кем дегенде бір талапқа қызмет L
көрсеткен болса.
Енді салыстырмалы приоритетті көпшілікке қызмет көрсету
жүйесінің
модельдеуші алгоритімін құрастыруға кірісейік.
Осы модельдеуші алгоритмнің сұлбасы керекті деректер мен бастапқы
шарттарды программаға енгізетін 1 - ші оператордан басталатыны анық. (10.4
- сурет).
Бұл деректер мен бастапқы шарттар мыналар:
модельдеу иитервалы[0, Тм];
осы жүйедегі каналдар саны k;
ағындар саны Q;
ағын талаптарының аралығын сипаттайтын кездейсоқ шамалардың
заңдылықтарының параметрлері;
қызмет көрсету уақытын белгілейтін үздіксіз кездейсоқ шамалардың
үлестірім заңының параметрлері;
барлық k каналдарының қызмет жасауға даярлық мерзімінің бастапқы мәні (tK
бос = 0);j
L және ф белгілерінің бастапқы мәндері (L = 1, ф = 1) жэне т.б.
Талаптар ағындары ең маңызды q=l номерлі (2-оператор) ағынның бірінші
талабын модельдеуден басталады (3, 4 - ші операторлар).
Ал 5,6,7- ші операторлар осы жүйені имитциялық модельдеудің аяқталу шартын
тексереді. Имитациялық модельдеудің аяқталуы үшін модельдеу барысында
шарты барлык Q ағындарға орындалуы қажет (5 - ші оператор). Яғни әр
ағынның соңғы талабының келу мерзімі модельдеу интервалынан асып кетуі
тиісті. Осы шарт орындалған ағындар саны 6-шы операторда есептеледі. Егер
бұл оператордыц мәні ағындар санына тең болса (7 - оператор) кезек
имитациялық модельдеудің нәтижелерін есептеу үшін 40 - шы операторға
беріледі. Бұл шарт орындалмаса, кезек 13 - ші операторға тиеді.
Енді 5 - ші оператордын шарты орындалмаған жағдайға оралайық.. Әрине,
имитациалық модельдеудің бас кезінде бұл шарт орындалмауы тиісті.
Сондықтан 8 - ші оператор имитациялық модельдеудің мына көрсеткіштерін
тіркейді:
- q ағынының жүйеге келіп түскен талаптарының саны ();
жүйеге келіп түскен барлық талаптар саны ;
әр кезекте тұрған талаптардың саны ( );
Келесі үш оператор (9, 10, 11) L=1 шарты орындалған жағдайда әр кезекке
бір талап қою әдісіне сәйкес,барлық Q кезекте бір-бір талап тұруын
камтамасыз етеді.
Ал L=1 және qQ шарттары орындалмаған жағдайда кезек 13 -ші операторға
беріледі және L белгісінің мәні (12-ші оператор) өзгертіледі (L=0).
Сондықтан алдағы уақытта талап кезектері бос орынды толтыру әдісімен
модельденуі тиіс.
13 - ші оператордан бастап модельдеуші алгоритмнің екінші кезеңі
басталады. Бұл кезекте тұрған талаптарды, олардың маңыздығына сәйкес,
қызмет көрсетуге алу тәртібі модельденеді. Салыстырмалы приоритет бойынша
қызмет көрсетілуге, қарастырылып отырған кезеңге дейін жүйеге келіп түскен
талаптардың ішінен ең приоритетті кезекте бірінші болып тұрған талап
алынуы тиіс. Соыдықтан қызмет көрсетуге лайықты талапты 1-ші кезектен
бастап іздеу жөн (13-ші оператор).
Келесі, 14-ші оператор осы кезекте тұрған талаптардың бар-жоқтығын
тексеріп, шарты орындалмаған, яғни бұл кезектің талаптары әлі
келмеген жағдайда, 15 және 16 операторлар арқылы маңызы бір саты төмен
келесі кезекті тексереді. Осы операциялар шарты әйтеуір бір кезекте
орындалғанша қайталана береді.
Бұл шарт орындалған жағдайда 17 - ші опратор осы кезектің бірінші
талабының келген мезгілінде бос каналдарының бар-жоқтығын анықтауға
кіріседі.
Егер осы талап келген мезгілде барлық каналдар бос болмаса бұл талап
бірінші босаған каналға кызмет көрсетілуге алынуы тиіс.
Ал қарама-қарсы жағдайда, яғни каналдардың босаған мезгілінде q кезегінде
бірде талап бомаса, каналды бос ұстамас үшін келесі маңыздығы төменірек
кезектерде талаптар бар-жоқтығы тексеріледі. Ол үшін кезек 18 - ші
операторға беріліп, q=Q орындалмаған жағдайда 16 - ші оператор арқылы
маңыздылығы төмен басқа кезектерде талаптар бар-жоқтығы анықталады.
Бұл тексеріс 14, 15, 16, 17, 18-ші операторлар тізбегі арқылы әйтеуір бір
кезекте шарты орындалғанша, немесе барлық Q кезекте мұндай шарт
орындалмағанша жүргізіледі.
Соңғы жағдайда 18-ші оператордан 19-шы операторға көшіп, маңыздылығына
қарамай, қызмет көрсетілуге ең бірінші келген талап алынуы тиіс.
20-шы оператор талаптың кезекте күткен уақытын, ал 21-ші оператор әр
нақтылы жағдайда талап пен каналдың кайсысының күткенін анықтайды. Канал
күткен жағдайда 22 - ші оператор каналдың бос тұрған уақытын есептейді:

Ал талап күтсе 23 - ші оператор

шартын тексереді. - q приоритетті талаптардың қызмет
көрсетуді күте алатын уақытының шекті мөлшері. (10.2)-шi шарт орындалмаса
бұл талапқа қызмет көрсетілмейді, сондықтан 24-ші оператор тиісті
парамегрлерге осы жағдайға сәйкес түзетулер енгізеді. Содан кейін кезек 25-
ші оператор арқылы, қызмет көрсетілмеген талаптардың санын есептейтін 38-
ші операторға беріледі.
(10.2) шарты орындалған жағдайда 26-ші оператор осы талаптың іс жүзінде
кезекте күткен уақытын есептейді. 27-ші оператор кезекті талапқа қызмет
көрсету уақытының мөлшерін модельдейді, ал 28-ші оператор осы қызмет
көрсетіліп болған, яғни каналдың қайтадан босаған, мезгілін анықтайды:

Модельдеуші алгоритімнің тағы бір кезеңі 29-32-ші операторларды қамтып,
талаптарға қызмет көрсетуге бастапқы кезде барлық k каналдарды бірінен соң
бірін қатыстырады. Бұл операторлар тобының жұмысы шарты орындалғанда
ғана басталып, барлық канал жұмысқа тартылып болғаннан кейін
белгісіне ноль мәнін тағайындаумен аяқталады. (32-ші оператор).
Ал 29-шы оператордың шарты орындалмаса, келесі талапқа қызмет көрсетуте ең
бірінші босаған канал (33, 34-ші операторлар) қатыстырылады. Дегенмен,
қызмет көрсетуге алынған келесі талапқа толық қызмет көрсетіледі деп
есептеу үшін (37 - оператор)

шарты орындалуы керек (36-шы оператор). Бұл шарт орындалмаған жағдайда ол
талапқа қызмет көрсетілмейді. (38-ші оператор).
37 және 38-ші операторлардан кейін кезек 39-шы оператор арқылы қайтадан 3-
ші операторға келесі талаптарды модельдеуге беріледі.
Ен соңғы операторлар тобы (40-47-ші операторлар) имитациялық модельдеудің
нәтижелерін өңдеуге бейімделген. Осы топтың ішіндегі бастапқы 5 оператор
әр приоритеттің көрсеткіштерін бөлек өңдеуге мүмкіншілік береді. Ал 45-ші
оператор жалпы көрсеткіштерді анықтайды.

3.2 Блок-схема моделирующего алгоритма

Рисунок 8 - Блок-схема многоканального СМО с ограниченной длиной
очереди

currentTime5:=0

Установка начальных
значений

Продолжение рисунка 8

exponen(oprNextZ(zF
orExponen[High(zFor
Exponen)],'Exponen'
)mForZByVichet,
LambdaForExponen)

TGamma(oprNextZ(zFo
rGamma[High(zForGam
ma)],'Gamma')mForZ
ByVichet,aF
orGamma)

Продолжение рисунка 8

exponen(oprNextZ(zForEx
ponen
[High(zForExponen)],'Ex
ponen')
mForZByVichet,LambdaFor
Exponen)

TGamma(oprNextZ(zForGam
ma
[High(zForGamma)],'Gamm
a')
mForZByVichet,aForGamma
)

Продолжение рисунка 8

Продолжение рисунка 8

Продолжение рисунка 8

Продолжение рисунка 8.

1:sOutput:='Рукопись #'+IntToStr(n)+'Время
прибытия:'+timer (vremya[1,2])+'
Интервал:'+timer(mashinistka1[n,0]) +' Время
Print:'+timer(mashinistka1[n,1])+'
Время:'+timer(currentTime1);
2:sOutput:='Рукопись #'+IntToStr(n)+'Время
прибытия:'+timer (vremya[2,2])+'
Интервал:'+timer(mashinistka2[n,0]) +' Время
Print:'+timer(mashinistka2[n,1])+'
Время:'+timer(currentTime2);
3:sOutput:='Рукопись #'+IntToStr(n)+'Время
прибытия:'+timer (vremya[3,2])+'
Интервал:'+timer(mashinistka3[n,0]) +' Время
Print:'+timer(mashinistka3[n,1])+'
Время:'+timer(currentTime3);
4:sOutput:='Рукопись #'+IntToStr(n)+'Время
прибытия:'+timer
(vremya[4,2])+Интервал:'+timer(mash inistka4[n,0
])+' Время Print:'+timer(mashinistka4[n,1])+'
Время:'+timer(currentTime4);

Продолжение рисунка 8

Продолжение рисунка 8

Продолжение рисунка 8

Продолжение рисунка 8

4.3 Описание логической структуры программы

Номер Описание
строки
1 Начало программы
2-5 Начальные установки
6-41 Описание типов
42-48 Описание процедур и функций
49-73 Описание своих типов данных
74-89 Функция(procedure) encode_time(), функция перевода цифр на
время
90-93 Функция exponen(), функция экспоненциального распределения
94-106 Функция Tgamma(), функция гамма распределения
107-124 Функция oprNextZ (), функция определения Z
125-162 Процедура PostroitOchered
163-253 Процедура записи данных в текстовый файл z.txt и result.txt
254-278 Функция summaVremeniOcheredi
279-306 Процедура printCurrientTime , запись в output
307-327 Процедура printOchered
328-444 Процедура TForm1.Nakonec
445-497 Процедура Начальные установки
498-515 Процедуры кнопок Button1, Button2,Button3

4.4 Вызов и загрузка
По необходимой директорий найти папку и запустить файл C:New
versionkurs.exe

4.5 Используемые технические средства
В процессе написания этой программы были использованы следующие

технические средства:

- процессор PentiumIV 2.8 МГц;
- ОЗУ 512 Мб;
- Видеокарта GeForceII 32Мб;
- HDD 40ГБ;
- Монитор SAMSUNG Sync Master 551S
- Microsoft Windows XP;
- DELPHI 7;
- Microsoft Office XP.

4.6 Входные данные
Входными данными являются строки ввода данных

1. Количество терминалов;
2. Альфа для гамма распределения;
3. Начальное значение Z0 для гамма распределения;
4. Лямда значение Z0 для экспоненциального распределения;
5. Начальное значение Z0 для экспоненциального распределения;

4.7 Выходные данные
1. Количество заявок;
2. Количество очереди;
3. Среднее время обслуживания заявок;
4. Средняя длинна очереди;
5. Средняя длинна пребывания заявок в очереди;
Результаты выполнения контрольной программы приведен в приложений Б

4.8 Ручной счет

z a для Gamma
z0=6
z1=25769802
z2=3436935910
z3=2891087210
z4=46181318
z5=1352129930
z6=3594089126
z7=3772282794
z8=2293608326
z9=721251274
z10=963330662

z a для Экспоненциального
z0=5
z1=21474835
z2=3579941141
z3=3840895107
z4=3617623845
z5=2558430707
z6=2279246389
z7=996085347
z8=1195512389
z9=1316870611
z10=2234431317

4.9 Контрольный пример

СПИСОК ЛИТЕРАТУРЫ

1. Бусиленко Н.П. Моделирование сложных систем.- М.: Наука, 1978.
2. Иванова В.М. Случайные числа и их применение.- М.: ФиС, 1984.
3. Шукаев Д.Н. Компьютерное моделирование.- Алматы: КазНТУ, 2004.
4. Шукаев Д.Н. Имитационное моделирование на ЭВМ: Учебное пособие.-
Алматы: КазНТУ, 1995. С.79.
5. Поляк Ю.Г. Вероятностное моделирование на ЭВМ.- М.: Сов. радио,
1971.
6. Пугачев В.С. Теория случайных чисел и их применение к задачам
автоматического управления.- М.: Физматгиз, 1969.
7. Шукаев Д.Н. Моделирование случайных закономерностей на ЭВМ.- Алма-
Ата: Кітап, 1991.
8. Лифщиц А.Л., Мальц Э.А. Статистическое моделирование систем
массового обслуживания.- М.: Сов. радио, 1978.
9. Шукаев Д.Н., Тусупова Б.Б. Моделирование систем массового
обслуживания: методическое указание по курсовому проекту.- Алматы:
КазНТУ, 2002.
10. Мартин Ф. Моделирование на вычислительных машинах. - М.:
Сов.Радио, 1972.
11. Нойлор Т. Машинные имитационные эксперименты с моделями
экономических систем. - М.: Мир, 1975.
12. Таха Х. Введение в исследование операций. В 2-х книгах. Кн. 2. М.:
Мир, 1985.
13. Советов Б.Я., Яковлев С.А. Моделирование систем. М.: Высшая школа,
2001.
14. Джейсул Н. Очереди с приоритетами. М.: Мир, 1973.

Приложение А
1. unit kurs;
2. interface
3. uses
4. Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,
5. Dialogs, StdCtrls, Spin, Math, ComCtrls, Buttons, ExtCtrls, jpeg;
6. type
7. TForm1 = class(TForm)
8. PageControl1: TPageControl;
9. TabSheet1: TTabSheet;
10. GroupBox2: TGroupBox;
11. GroupBox3: TGroupBox;
12. Label4: TLabel;
13. Label5: TLabel;
14. EditZ0ForGamma: TEdit;
15. GroupBox4: TGroupBox;
16. Label7: TLabel;
17. Label8: TLabel;
18. EditLambdaForExponen: TEdit;
19. EditZ0ForExponen: TEdit;
20. Button1: TButton;
21. TabSheet2: TTabSheet;
22. output1: TMemo;
23. TabSheet3: TTabSheet;
24. TabSheet4: TTabSheet;
25. TabSheet5: TTabSheet;
26. output2: TMemo;
27. output3: TMemo;
28. output4: TMemo;
29. TabSheet6: TTabSheet;
30. TabSheet7: TTabSheet;
31. TabSheet8: TTabSheet;
32. output5: TMemo;
33. Button2: TButton;
34. Button3: TButton;
35. EditAForGamma: TEdit;
36. Memo1: TMemo;
37. Image1: TImage;
38. Image2: TImage;
39. Memo2: TMemo;
40. Image3: TImage;
41. Memo3: TMemo;
42. procedure Button1Click(Sender: TObject);
43. procedure startSettings;
44. procedure nakonec;
45. procedure FilePrint;
46. procedure Button2Click(Sender: TObject);
47. procedure Button3Click(Sender: TObject);
48. private{ Private declarations }
49. public { Public declarations }
50. end;

Продолжение приложения А
51. var { MAIN}
52. Form1: TForm1;
53. zga:real;
{Cтруктура массива: mashinistka1[0,0]=содержит интервал (время)
прибывания 1-го рукописного материала для 1-ой машинистки;
mashinistka1[0,1]=содержит время набора текста первого рукописного
материала для 1-ой машинистки}
54. mashinistka1:array of array of real;
55. mashinistka2:array of array of real;
56. mashinistka3:array of array of real;
57. mashinistka4:array of array of real;
58. mashinistka5:array of array of real;
{Cтруктура массива ochered1[0,0]=интервал (время) прибывания для 1-го
рукописного материала который стоял в очереди для 1-ой машинистки
ochered1[0,1]=время набора текста для 1-го рукописного материала который
стоял в очереди для 1-ой машинистки в очереди всегда будут 25-35
рукописей.}
59. ochered1:array of array of real;
60. ochered2:array of array of real;
61. ochered3:array of array of real;
62. ochered4:array of array of real;
63. ochered5:array of array of real;
{ukazatelOcheredi[1,1]-ukazatel na nachalo ocheredi dlya 1-oi mashinistki
ukazatelOcheredi[1,2]-ukazatel na konec ocheredi dlya 1-oi mashinistki}
64. ukazatelOcheredi: array[1..5,1..2] of integer;
{vremya-massiv dlya ucheta vremeni,
vremya[1,1]=esli 1-ya mashinistka rabotaet to ravno 1, esli net to 0.
Zavisit ot vremeni
vremya[1,2]=pokazivaet skolko vremeni rabotaet 1-ya mashinistka}
65. vremya:array[1..5,1..2] of real;
{zForExponen массив истории зетов (случайных чисел) для нахождения
интервал (время) прибывания по Exponencialnomu, zForGamma массив истории
зетов (случайных чисел) для нахождения времени обработки по Равномерному}
66. zForExponen,zForGamma: array of cardinal;
{workTime -время работы машинисток в минутах}
67. LambdaForExponen:real;
{aForGamma -параметр Альфа для нахождения времени обдумывания по Гамма}
68. aForGamma:real;
69. kolOcheredi,dlinaOcheredi:cardinal;
{м и а параметры для нахождения случайных цичел по методу вычета}
70.
aForZByVichet,mForZByVichet,pozicia 1,pozicia2,pozicia3,pozicia4,pozici a5
:cardinal;
{currentTime1 -условная переменная, для учета текущего времени для первой
машинистки}
71.
nacaloRaboti,konecRaboti,nacaloObed a,konecObeda,workTime,currentTime1, cu
rrentTime, currentTime3,currentTime4,currentTi me5:real;
72. implementation
73. {$R *.dfm}

74. function timer(minsec:real):string;
75. var
76. s1,s2,s3,ss:integer;
77. secund,minute,hour:string;
78. begin
79. ss:=round(minsec);
80. s2:=ss mod 60;

Продолжение приложения А

81. ss:=ss div 60;
82. s1:=ss mod 60;
83. ss:=ss div 60;
84. s3:=ss div 60;
85. hour:=inttostr(s3);
86. minute:=inttostr(s1);
87. secund:=inttostr(s2);
88. timer:=concat(hour,' : ',minute,' : ',secund);
89. end;

общая формула экспоненциального -1lambda*ln(z)
90. function exponen(z,lambda:real):real;
91. begin
92. exponen:=-1lambda*ln(z);
93. end;

общая формула Gamma
94. function TGamma(oprNextZ:real;zga:real):real ;
95. var
96. zg:real;
97. tgam:real;
98. fs:real;
99. begin
100. fs:=1;
101. zg:=oprNextZ;
102. fs:=fs*zg;
103. if(fs=0) then fs:=1;
104. tgam:=abs((-ln(fs)zga));
105. TGamma:=tgam;
106. end;

{Функция для нахождения случайных чисел по методу вычетов общая формула
z(n+1)=a*zn(mod m), zn -текущее число a(aForZByVichet) -положительное число
м(mForZByVichet) -число, которое больше чем количество итерации }
107. function oprNextZ(z0:cardinal;s:string):card inal;
108. var a,zNext:cardinal;
109. begin
110. zNext:=(aForZByVichet*z0)mod mForZByVichet;
111. if s='Exponen' then
112. begin
113. a:=High(zForExponen)+2;
114. SetLength(zForExponen,a);
115. zForExponen[a-1]:=zNext;
116. end
117. else
118. begin
119. a:=High(zForGamma)+2;
120. SetLength(zForGamma,a);
121. zForGamma[a-1]:=zNext;
122. end;

Продолжение приложения А

123. oprNextZ:=zNext;
124. end;

125. procedure postroitOchered;
126. var i:integer;
127. begin
128. for i:=pozicia1 to 35+pozicia1 do
129. begin
130. SetLength(ochered1,High(ochered1)+2 );{SetLength -выделяет для
динамического массива место в памяти}
131. SetLength(ochered1[High(ochered1)], 2);
132.
ochered1[High(ochered1),0]:=exponen (oprNextZ(zForExponen[High(zForExpo ne
n)],'Exponen')mForZByVichet,Lambda ForExponen);
133.
ochered1[High(ochered1),1]:=TGamma( oprNextZ(zForGamma[High(zForGamma)] ,'
Gamma')mForZByVichet,aForGamma);
134. end;
135. for i:=pozicia2 to 35+pozicia2 do
136. begin
137. SetLength(ochered2,High(ochered2)+2 );{sozdalaem element dlya massivov
ocheredi}
138. SetLength(ochered2[High(ochered2)], 2);
139.
ochered2[High(ochered2),0]:=exponen (oprNextZ(zForExponen[High(zForExpo ne
n)],'Exponen')mForZByVichet,Lambda ForExponen);
140.
ochered2[High(ochered2),1]:=TGamma( oprNextZ(zForGamma[High(zForGamma)] ,'
Gamma')mForZByVichet,aForGamma);
141. end;
142. for i:=pozicia3 to 35+pozicia3 do
143. begin
144. SetLength(ochered3,High(ochered3)+2 );
145. SetLength(ochered3[High(ochered3)], 2);
146.
ochered3[High(ochered3),0]:=exponen (oprNextZ(zForExponen[High(zForExpo ne
n)],'Exponen')mForZByVichet,Lambda ForExponen);
147.
ochered3[High(ochered3),1]:=TGamma( oprNextZ(zForGamma[High(zForGamma)] ,'
Gamma')mForZByVichet,aForGamma);
148. end;
149. for i:=pozicia4 to 35+pozicia4 do
150. begin
151. SetLength(ochered4,High(ochered4)+2 );
152. SetLength(ochered4[High(ochered4)], 2);
153.
ochered4[High(ochered4),0]:=exponen (oprNextZ(zForExponen[High(zForExpo ne
n)],'Exponen')mForZByVichet,Lambda ForExponen);
154.
ochered4[High(ochered4),1]:=TGamma( oprNextZ(zForGamma[High(zForGamma)] ,'
Gamma')mForZByVichet,aForGamma);
155. end;
156. for i:=pozicia5 to 35+pozicia5 do
157. begin
158. SetLength(ochered5,High(ochered5)+2 );
159. SetLength(ochered5[High(ochered5)], 2);
160.
ochered5[High(ochered5),0]:=exponen (oprNextZ(zForExponen[High(zForExpo ne
n)],'Exponen')mForZByVichet,Lambda ForExponen);

Продолжение приложения А
161.
ochered5[High(ochered5),1]:=TGamma( oprNextZ(zForGamma[High(zForGam
ma)],'Gamma')mForZByVichet,aForGam ma);
161. end;
162. end;

163. procedure TForm1.FilePrint;
164. var f,f1:textfile;
165. i:integer;
166. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.