Логикалық есептер және оны шығару жолдары

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

эмблема Қазақстан Республикасы Білім және ғылым министрлігі

Қарағанды облысының Білім басқармасы

Облыстық мамандандырылған дарынды балаларға арналған

«Мұрагер» мектеп-интернаты

Математика пәнінен курстық жұмыс

Логикалық есептер және оны шешу әдістері

Орындаған : Хасенова Амина

Аккисева Шадияр

8 «С» - сынып оқушылары

Жетекшісі :

Есимжанова Г. Ш.

Математика пәні мұғалімі

Қарағанды 2014

Мазмұны

Кіріспе . . . 3

Негізгі бөлім . . . 4-13

1. 1. Диофант әдісі . . . 4-6

1. 2. Есептерді ребус түрінде шешу . . . 7

1. 3. Таблицалық тәсілмен шешілетін логикалық есептер . . . 8

1. 4. Сандардың бөлінгіштігіне есептер . . . 9

1. 5. Граф арқылы дәлелдеу . . . 10-13

Қорытынды . . . 14

Қолданылған әдебиеттер тізімі . . . 15

Кіріспе

Мақсаты: Логикалық есептерді шығару және қолдану жолдарын зерттей отырып, өмірде жүйені қолдана білуге дағдыландыру.

Міндеттері:

1) Бүтін сандар өрісінде сандардың қасиетін қолдану:

а) диофант әдісі;

б) ребустар:

в) таблицалық тәсіл;

2) Санның бөлінгіштік қасиетін қолдану;

3) Граф арқылы дәлелдеу;

4) Сіріңкені қолданып есептер шығару;

5) Әр түрлі есептер.

Анықтама. Арнайы формула қолдануға келмейтін, әрқайсысына өзінше талдау жасауды қажетсінетін есептерді логикалық есептер дейміз.

Өзектілігі. Логикалық есептерді шығару, өз бетімен есептер құру, ғаламтор жүйесін қарау, баспасөз беттерінен материалдар жинау арқылы логикалық есепті шеше білу қызығушылықты арттыра отырып, өз бетімен жұмыстана білуге үйретеді. Логикалық есептер шығаруда өзінің білім деңгейі көтеріліп, кең ауқымды есептерді зерттеу, ойлау қабілетін дамытып, жаңа іс-қимылға жетелейді. Пәндік икемділігі қалыптасады.

Диофант әдісі

Диофант теңдеулерін III ғасырларда өмір сүрген Диофант Александрийский ойлап тапқан еді.

Прах Диофанта гробница скрывает: вглядись - и камень

Мудрым искусством раскроет покойного возраст:

По воле богов шестую часть жизни он был ребенок,

А еще половину шестой - встретил с пушком на щеках.

Только прошла седьмая на любимой он женился.

С ней пять лет прожив, сына дождался мудрец.

Но полжизни своей тешился отец лишь сыном:

Рано могила ребенка у отца забрала.

Лет двое по два отец оплакивал сына.

А по годам этим и сам встретил он конец свой печальный …

Математикада әр түрлі теңдеулер мен теңсіздіктер тек бүтін сандар жиынында қарастырылады. Мысалы, оған анықталмаған теңдеулер әдісі бойынша шешілетін қарапайым диофант теңдеулерін жатқызуға болады.

Есептер:

№31 есеп. Бір товар 23 сом тұрады. Сатып алушыда тек 3 сомдықтар, ал кассирде 5 сомдықтар бар. Ешбір сомды ұсақтамай-ақ кассирмен сатып алушы қалай есептеседі?

Ш е ш у і : х, у - керекті 3 және 5 сомдықтар саны болсын. Есеп шарты бойынша 3 x -5 y =23 болуы керек. Біз екі белгісізі бар бір теңдеу алдық. Бұл түрдегі теңдеулерді анықталмаған теңдеу деп атаймыз, оның сансыз көп шешуі бар. Біз көбінесе белгісіздердің теңдеуді қанағаттандыратын шектеулі мәндерін ғана іздейміз. Жоғарыда айтылғандай тек бүтін сандар жиынында ғана қарастырсақ,

x= $\frac{23 + 5y}{3}$ не y= $\frac{3x - 23}{5}$ .

Бірінші теңдеудегі у -ке 0, 1, 2, . . . мәндерін берсек, у - тің кейбір мәндері үшін х шамасының мәндері бүтін болады, мысалы, y=2 десек, x=11. Демек, сатып алушы 11 үш сом бергенде де, 2 бес сомдық қайтарып алған. Есеп шартына байланысты құрылған теңдеудің сансыз көп шешуі бар. Олар: 1) y=5, x=16; 2) y=8, x=21; 3) y=11, x=26 т. с. с.

Күнделікті өмірде мұндай есептер жиі кездеседі.

Бұл теңдеулерді

ax+by=c (1)

деп жалпы түрде жазуға болады, мұндағы a, b, c- нольден өзгеше бүтін оң сандар.

$\alpha, \beta\ қос\ саны\ ($ 1) теңдеудің түбірлері делік, олай болса, оны

a $\alpha + b\beta = c$ (2)

деуге болады, (1) теңдеуден (2) теңдеуді мүшелеп шегерсек, a(x - $\alpha) + b(y - \beta) = 0$ Жауабы: Бұл құрылған теңдеудің сансыз көп шешуі бар.

Есептерді ребус түрінде шешу.

Бұл түрге арифметикалық ребус, әріпті, жұмбақ суретті ребустар т. б. жатады.

Кейбір цифрлары жұлдызшалармен, дөңгелектермен немесе әріптермен алмастырылған арифметикалық амалдар қолданылатын есептеулерді арифметикалық ребустар деп атаймыз. Басқаша айтқанда, әр түрлі таңбалармен не әріптермен, не суреттермен көрсетілген жұмбақтар ребустар делінеді. Мұндағы жұлдызшалар, дөңгелектер, әріптер анықталған белгілі бір цифр бірнеше рет қайталануы немесе тіпті мүлдем қолданылмай қалуы мүмкін.

№34 Есеп. Жұлдызшалардың орындарына жазылатын цифрларды табыңыздар:

$\mathbf{\times}\frac{\begin{array}{r} \mathbf{6*} \\ \mathbf{**} \end{array}}{\begin{array}{r} \mathbf{**} \\ \mathbf{**}\mathbf{*} \end{array}}$

**6

Ш е ш у і : Көбейтуден екі көбейткіштіңде екі таңбалы сан екенін және олардың 1 не 6 цифрымен аяқталатының байқаймыз. Бұл тек 11 болған жағдайда ғана жүзеге асады, ендеше, көбейтіндінің соңғы цифры 6. Олай болса, ізделінді көбейтінді: 66 $\bullet$ 11=726

Жауабы: 66*11=726

Таблицалық тәсілмен шешілетін логикалық есептер.

5^{x} + 2

17^{y}

n: 0

x: 0

y: 0

5x+25^{x} + 2: 3

17y17^{y}: 1

n: 1

x: 1

y: 1

5x+25^{x} + 2: 7

17y17^{y}: 17

n: 2

x: 2

y: 2

5x+25^{x} + 2: 27

17y17^{y}: 289

n: 3

x: 3

y: 3

5x+25^{x} + 2: 127

17y17^{y}: 4913

n: 4

x: 4

y: 4

5x+25^{x} + 2: 627

17y17^{y}: 83491

n: 5

x: 5

y: 5

5x+25^{x} + 2: 3127

17y17^{y}: 1419347

n: 6

x: 6

y: 6

5x+25^{x} + 2: 15627

17y17^{y}: 241288929

Бірнеше белгісізі бар теңдеудің бүтін оң түбірлерін іздеу керек болса, ондағы теңдеуге қатынасатын өрнектерді зерттеп, олар анықталатын жиындардан белгісіздерге біртіндеп сан мән береміз. Теңдеуді қанағаттандыратын бүтін сандарды таңдап аламыз.

Сандардың бөлінгіштігіне есептер

Бір санды екінші санға бөлу математикалық есептеулерде өте маңызды роль атқарады. Сандардың бөлінгіштігі кез келген натурал санды жай сандардың көбейтіндісі түрінде жіктеп жазуға болады деген теоремаға және қатар тұрған сандардың қасиетіне сүйенеді. Безу теоремасының салдары ретінде қалдықпен бөлу, қысқаша көбейту формулалары, Ньютон биномы формуласы және индукция методтары көмегімен сандарды бір біріне бөледі.

№47 Есеп. Айырманың 5-ке бөлінетінін дәлелдеңдер:

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3}^{2000}$ $7^{2000}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3$ $7^{3}$

Ш е ш у і : Бөлшектер айырмасынан $3^{1999}$ - $7^{1997}$ айырмасы шығады. Мұны төмендегіше түрлендіреміз: ( $3^{1999} + 7^{1999}$ ) $-$ ( $7^{1997}$ - $7^{1997}$ ) $-$ ( $7^{1997} + 7^{1999}$ ) . Санның негізі бөлінетін санға, оның дәрежесі де бөлінеді деген тұжырым бойынша:

3+7= $10^{6}$ , $10^{6} \div 5;$

7-7=0, 0 : 5;

$7^{1997} + 7^{1999}$ = $7^{1997}\left( 1 + 7^{2} \right) = 7^{1997} \bullet 50$

яғни, $7^{1997} \bullet 50\ :5$

Дәлелденді

[ Г. ] 3. 2

а саны 3-ке еселік. Ал b саны 8-ге еселік. а*b саны 24-ке еселік екенін дәлелдеу керек.

Дәлелдеу:

а=3n, b=8n, олай болса

а • b =3n • 8n=24n ²

Көбейткіштердің біреуі 24, ол 24-ке еселік. Ендеше а·b саны 24-ке еселік болады, яғни бөлінеді.

Граф арқылы дәлелдеу

Граф арқылы есептеуді Леонард Эйлер ойлап тапқан еді.

Леонард Эйлер(1707-1783) математик, механик, физик және астроном. Граф деп бірнеше нүктелерден не сандардан тұратын әр түрлі жиындарды не фигураларды айтады. Әдетте әр түрлі жиындығы бар элементтер өзара үзік не тұтас сызықтармен қосылады. Сонымен, граф деп берілген жиындардағы нүктелерді қосатын сызықтар тобын айтады. Граф арқылы объектілер арасындағы байланыстарды айқын көрсетуге болады.

№57 Есеп.

Дүйсенбі күнгі сабақ кестесін құру кезінде үш мұғалім мынадай өтініш айтты: 1) математика не бірінші не екінші, 2) тарих не бірінші не үшінші, 3) әдебиет не екінші не үшінші болсын.

Қанша тәсілмен мұғалім өтінішін орындауға болады?

Ш е ш у і :

Математика, тарих, әдебиеттің бас әріптерін бір жиын, сабақтардың 1, 2, 3 деген ретінен екінші жиын құралық. Мұғалімдердің өтініштеріне қарай екі түрлі жағдайды қарастырамыз.

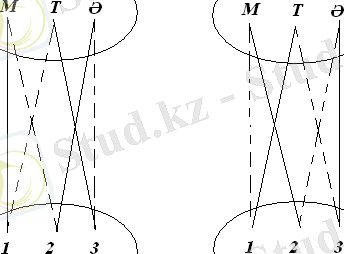
Математиканы 1 сабаққа қойсақ, онда тарих тек үшінші ғана болады; тарих 1 қойылмайды, онда әдебиет 2 сабаққа қойылған болады; ол 3 сабаққа қойылмайды. Сонымен математика бірінші, әдебиет екінші тарих үшінші болады.

Жауабы: 1-математика, 2-әдебиет, 3-тарих

2- есеп : Бірнеше ұл балалар вокзалдың алдында кездесті. Олар бір-бірімен қол ұстасып амандасты. Егер 10 қол амандасып ұстасса, онда қанша ұл бала қалаға кетті?

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.