Ассерция негізіндегі HDL модельдерін верификациялау инфрақұрылымының аналитикалық моделі


МАЗМҰНЫ
- КІРІСПЕ3
- НЕГІЗГІ БӨЛІМ
Верификация инфрақұрылымының аналитикалық моделі . . . 4
- ҚОРЫТЫНДЫ . . . 11
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ. . . 12
КІРІСПЕ
Жүйені жобалаудың әр түрлі аспектілері үшін әр түрлі тілдер жүзеге асырылды. C/C++ кірістірілген жүйелердің бағдарламалық қамсыздандыруын жүргізуде айрықша басымдылықпен қолданылды.
HDL - тілдері аппаратураны сипатту үшін, VUDL және Verilog сандық сұлбаларды жобалау мен синтездеуде пайдаланылды. Vera верификациялау тілі- ASIC- жобаларының ішкі верификациясы үшін қолданылатын, Sun Micro System бірлестігінің тудырған өнімі. Кейін VERA компиляторымен VERA тілі System Science фирмасына сатылып, соның салдарынан Synopsys бірлестігіне көшеді. Қазіргі таңда, Synopsys бірлестігісVCS компиляторымен қолданатын, Vera тілінің жаңа нұсқасын - Open Vera -ны шығарды. Верификация, валидация, ассерция сияқты басты ұғымдар арасындағы қатынастарды түсіну үшін келесі анықтамалар енгізіледі.
Верификациялау - жобалаудың әрбір кезеңінде кіріс суреттелуінің шығысқа формальды түрденуінің дұрыстығын анықтау үшін компоненттер немесе жүйе анализінің процесі.
Валидация - әрбір кезеңдегі жобалау орындалғаннан кейін, спецификацияның басты талаптарына сәйкестігін тексеру жолымен, жүйенің және оның компоненттерінің жұмыс істеу қабілетін анықтау процесі.
Сертификаттау - спецификацияның оның тағайындалуы бойынша қолданылуы кезіндегі, талаптарына жүйе анықтылығының экспертті кепілдігі.
Ассерция - синтезді орындауға дейін және кейін тестті әрекетте жобаны модельдеу кезінде, спецификация талаптарына қатысты жобалау қателерін ерте анықтау үшін арналған жүйелік деңгейдің инверсты HDL-пікірі.
Верификация инфрақұрылымының аналитикалық моделі
HDL моделінің жалпыланған күйін идентификациялау үшін эталонды реакциялар критикалық нүктеде уақыт бойынша және ортада жасалады. Содан кейін HDL моделі үшін оны салыстыру жолымен эталонды және экспериментальды реакцияларды тексеріп, ассерционды векторды жасауға керек, яғни уақыт бойынша және ортада обьекттердің компоненттерін салыстыру күйін бейнелейді. Ассерционды векторды HDL моделінің жобалауынан тәуелсіз етіп жасау. Ассерционды және функционалды модельдерді паралельді және бір-біріне тәуелсіз модельдеу ортасында жүзеге асырады.
Ассерционды модель эталонды құрылымның кеңістік-уақыттық бірнеше маңызды нүктелердің обьекттерде тәртібінің ауытқуын анықтайды. Верификация инфрақұрылымының аналитикалық моделі келесі түрде көрсетілген (P - жоба спецификациясы, S - soft-модель, A - ассерционды модель, T - Testbench, F - фукнционалды жабулардың себеті, d - қателерді диагностикадан өткізу модулі және C - қателерді диагностикадан өткізу шарты) . Ассерция форматы HDL жобалау моделінің форматымен сәйкес келуі қажет. Ассерциялар Testbench және MUV қолдану арқылы HDL моделінің семантикалық қателіктерін тексеруге арналған. Верификация инфрақұрылымының аналитикалық моделі келесі түрде болады:
Мұнда P- жобалау спецификациясы; S- программалық модель,
F- функционалды жапқыштың кәрзеңкесі,
T- Testbench,
А- ассерционды модель,
және С- қателіктерді тексеретін шарттар мен модульдер,
Мұнда
(2)
(3)
(1) формула спецификацияға қатысты функционалдығын тексеретін тесттің (testbench) толық шартын анықтайды. (2) теңдеу верификациялық инфрақұрылымның атрибуттарын қолдану арқылы жүйеліктен регистрлеуге өткенде жобалау қателігін есептейтін функция. (3) теңдік сандық кристалдағы жүйені экслуатациясы кезінде ақауын табуға реттелген.
Ассерцияның қасиеттері мен типтері. 1) Ассерцияның шекаралық мәні жобаның диверсиялық моделі, іс жүзінде ассерциялық операторлардың саны - жоба кодының 5%-ы. 2) Лездік және біртактілік ассерциялар жоба моделіне жатады, инверсты if-операторлар нысанында бағдарлама мәтініне қойылады. 3) Параллельді ассерциялар (циклдық немесе көп тактілі) - орындалатын жоба моделіне тәуелсіз және параллельді модельденеді.
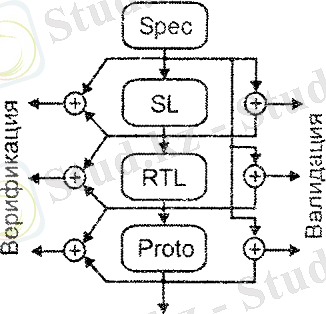
1-сурет. Валидация және верификация процесстерінің әрекеттестігі
Ассерционды артықтық спецификациямен анықталған функционалды компоненттердің уақыттық фреймдерінің саны шектік санға тең болатын HDL моделінің критикалық нүктесінің функциясы болып табылады. Априорлы координаттарға ассерция векторы Х мәнін біріктіреді. Содан кейін критикалық координатасы анықталады, яғни сандары берілген тексеру тереңдігімен программалық блоктартардың қателіктерін іздеу кезіндегі верификациялық эксперимент жүргізгенде ғана жеткілікті болады. Мұндай координаталар бірліктерде сәйкестенеді. А векторының Әрбір координатасына сәйкесінше бағдарламалық кодтың транзакциялық кескінінің барлық жоғарыдағы бастамашылардың тізімі қойылады. Вектор координаталарына кез келген басқа пішінде берілген ұлы бастамашылардың тізімі немесе транзакциялық кескіннің қол жеткізу матрицасы сәйкес келеді. Нақты А векторы элементтерінің екілік күйі келесі теңдеумен анықталатын, L ақаулы бағдарламалық блоктар d(A) тізімін сөзсіз диагностикадан өткізу рәсімін жүрзізеді.
(4), (5) теңдеулер жүйесі ассерционды күйдегі векторларды қолданып, жалғыз және еселі қателіктерді іздеуге арналған. Ассерционды вектордың ұзындығы графтағы биіктік санына немесе HDL кодының функционалды-логикалық құрылымындағы программалық блок санына тең. Верификация ортасындағы векторлық модель келесі түрге ие:
(6)
Модельдеу үдерісінде Testbench және HDL модельдерінің реакцияларын салыстырады, яғни ассерционды вектордың координата күйін жасайды:
Содан кейін маңызды {0, 1} ассерция векторының координатасына конъюнкция операциясын (4), (5) анықталған тәртіптердің біреуін қолдана отырып, программалық блоктардың тізімін алу үшін қолданады.
Келесі мысалда ақаулы блоктарды диагностика технологиясын қарастырамыз. HDL моделінің функционалды-логикалық графы берілсін
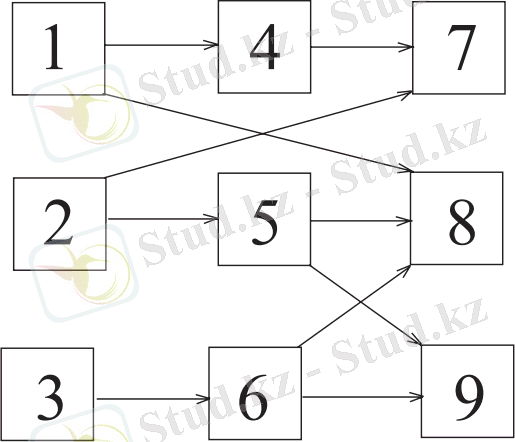
Өзара байланысқан граф құрылымын келесі қол жетімді матрицадан көреміз:

Диагностикалаудың векторлық моделі (6) теңдікте берілген, қолжетісді матрицадан алынған кез келген граф биіктігін блоктар-бастамасының тізімін қамтиды. Кез келген граф биіктігінде ассерцияға байланысты қойылады, яғни модельдеу процесі {0, 1} мәндері арқылы алдын-ала анықталуы мүмкін. Қазіргі жағдайда векторлық модель қателікті программалық блоктар (6) теңдей (7) граф түріне өзгереді:

Келесі мысалда алғашқы екі вектордан ассерционды вектордың координатасының негізгі анализінен ақаулы блоктардың тізімінен мардымсыз процесті өңдеуді шығарамыз. Жалғыз дефекттің тізімінің есептелу процедурасы келесі түрге ие:

Көптеген ақаулы блоктар үшін осындай ассерция векторы дефектті модульдің көп сандарын қамтиды.

Верификация және тестілеу стратегияларының, time-to-market параметрін қысқартуға бағдарланған, технология қосымшалары үшін әртүрлі модельдері бар. Верификацияның итеративті процесі өнім спецификациясынан алынған HDL-жүйелік деңгей моделінің қателерін жөндеуге бағдарланған.
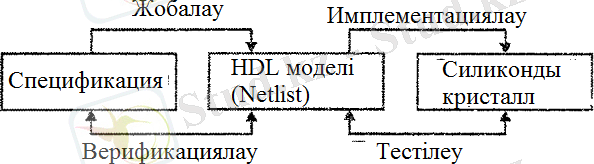
2-сурет. Жобаны жасау стратегиясы
HDL-моделді верификациялау және тестілеу инфрақұрылымы 3-суретте келтірілген. Онда жоғарғы деңгейдің формалды тілінде суреттелген жоба спецификациясы функционалдық жабу түріндегі тест сапасын бағалау метрикасын құру, жобаның HDL-модельдері, эталонды реакциялы - Testbench, басты модельге қосымша болатын, жоба дұрыстығы мен тексеруін тездету үшін қажетті, ассерционды құрылым үшін бастапқы ақпарат болып табылады.
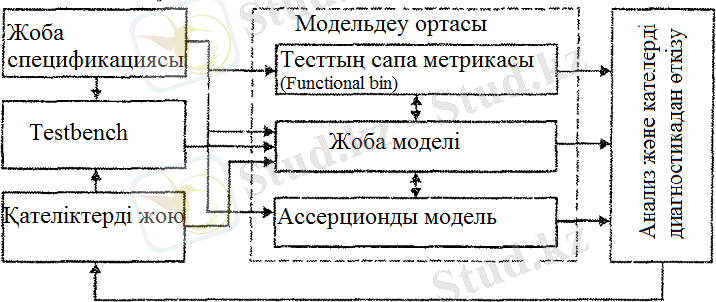
3-сурет. Жобаны верификациялау ортасы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz