Фурье қатары мен интегралының сигналдардың спектрлік талдаудағы қолданылуы және сызықтық электр тізбектерінің жиіліктік сипаттамалары


МАЗМҰНЫ
- КІРІСПЕ
- НЕГІЗІГІ БӨЛІМ
- Фурье қатары
- Фурье интегралы түріндегі сигнал энергиясының таралуы
- Сигналды спектралдық талдауда Фурье қатарының қолданылуы
- ҚОРЫТЫНДЫ
- ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
КІРІСПЕ
Фурье қатары - [а, b] кесіндісінде ортонормаланған φ1(х), φ2(х), . . . , φn(х), . . . функциялар жүйесі бойынша f(x) функциясының Фурье қатары деп
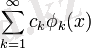
қатарын айтады. Мұндағы сk Фурье коэффициенттері:
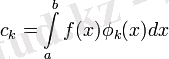
1, cosnx, sinnx, n=1, 2, . . . , тригонометриялық жүйесіндегі Фурье қатары:
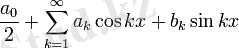
мұндағы a0, ak, bk - Фурье коэффициенттері.
Әртүрлі техникалық мақсаттарға арналған әрбір электротехникалық құрылғыларда небір энергетикалық өзгерулер пайда болады. Олардың көбісінде электр энергиясы бұл құрылғының жеке бөлшектері арасына қайта бөлінеді. Электр тізбегі есебінің тәжірибелік қолданысы өте қажет. Бұл курстық жұмыста сызықты тармақты электр тізбегін талдауды спектрлі әдіспен жүргізу керек.
Спектральдық талдау жасау үшін Фурье қатары қолданылатыны белгілі. Талдаудың математикалық әдісіне қысқаша шолу жасайық.
1. Фурье интегралы түріндегі сигнал энергиясының таралуы
Периодтық емес кернеу u ( t ) Фурье интегралы түрінде берілсін:
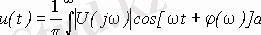
Берілген кернеу қосылған R =1 Ом резистивтік кедергіде белгіленетін W энергиясын анықтайық. Сонда мынаны аламыз:
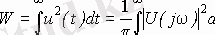 (1. 1)
(1. 1)
(1. 1) -да математикадан белгілі Рэле теоремасы қолданылған. Алынған байланыстан U(jω) 2 функциясы ағымдағы жиілікте ω жиілік жолағына 1 рад/с келетін сигнал құраушыларының энергиясын сипаттайтындығы белгілі. Бұл функцияны сигнал энергиясының спектральдық тығыздығы деп атайды.
Қорыта келгенде U(jω) 2 функциясы бойынша периодтық емес сигналдың энергетикалық манызды бөліктері жайлы сөз қозғауға болады. 1. 1- суретте тікбұрыш пішінді видеоимпульс энергиясының спектральды тығыздығының графигі келтірілген. Ол мына формула бойынша есептелінген:
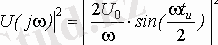
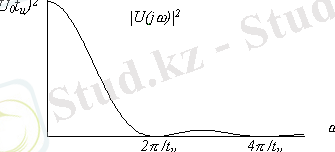
1. 1-сурет
Импульс энергиясының негізгі бөлігі төменгі жиіліктер облысында тұрақтанған. Импульс энергиясының 90%нан көбі негізгі жолаққа келеді деп айтуға болады, яғни ω = 0ден ω = 2 π / t и ға дейінгі жиілік жолағына. Көбінесе практикалық қосымшаларда бұл жиіліктер жолағы импульс спектрінің ені ретінде қабылданады. Импульс ұзақтығы неғұрлым аз болса, оның спектрінің ені соғұрлым көп болады .
2. Сигналды спектралдық талдауда Фурье қатарының қолданылуы
Берілген әдістің негізі ретінде Фурьенің кері түрлендіруі алынады. Кіріс дабылдың спектральді тығыздығы және сызықтық буынның тарату коэффициенті белгілі болған жағдайда, шығыс дабылының спектральді тығыздығы
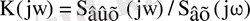 (2. 1)
(2. 1)
өрнегіне сәйкес келесідей жазылады:
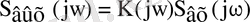 (2. 2)
(2. 2)
Әрі қарай Фурьенің кері түрлендіруіне сәйкес,
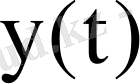 шығыс дабылы есептеледі. Ескеретін жайт, Фурье түрлендіруін қолданылу шарты - интеграл астындағы функцияның абсолютті интегралдануы. Бұл шарт берілген әдісте қолданылатын дабылдар класын азайтады.
шығыс дабылы есептеледі. Ескеретін жайт, Фурье түрлендіруін қолданылу шарты - интеграл астындағы функцияның абсолютті интегралдануы. Бұл шарт берілген әдісте қолданылатын дабылдар класын азайтады.
3. Фурье түрлендіруінің Лаплас түрлендіруімен байланысы
Талдаудың екі түрі мен сипаттамалардың екі типі. Талдаудың екі түрі - уақыттық және спектральді (басқаша атауы - жиіліктік) - сызықтық динамикалық жүйелерді зерттеуде қолданылады. Сәйкесінше, сипаттамалардың екі типі сызықтық құралдың жұмысын анықтайды, олар: уақыттық және жиіліктік.
Уақыттық зерттеудің негізі болып Лапластың кері және тура түрлендіруі алынсса, ал спектральді зерттеу үшін Фурьенің кері және тура түрлендіруі алынады.
Лапластың түрлендіруіне сәйкес, құрылғының уақыттық сипаттамаларды табуға мүмкіндік беретін беріліс функциясы
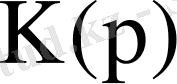 анықталса, Фурье түрлендіруіне сәйкес, объектінің жиіліктік қасиеттерін анықтайтын тарату коэффициентін
анықталса, Фурье түрлендіруіне сәйкес, объектінің жиіліктік қасиеттерін анықтайтын тарату коэффициентін
 табады. Фурье интегралдары Лаплас түрлендіріуінің жеке жағдайы болып саналғандықтан,
табады. Фурье интегралдары Лаплас түрлендіріуінің жеке жағдайы болып саналғандықтан,
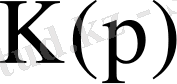 мен
мен
 арасында уақыттық сипаттамалардан жиіліктікке және керісінше көшуге мүмкіндік беретін тура байланыс бар.
арасында уақыттық сипаттамалардан жиіліктікке және керісінше көшуге мүмкіндік беретін тура байланыс бар.
Сызықтық жүйенің қарапайым буынын - төртұштықты қарастырайық.
Жоғарыда айтылған сипаттамаларды дәл осы төртұштыққа үш тестілік
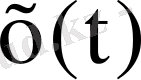 кіріс дабылы барысында анықтайық: синусоидалы, бірлік секіріске және бірлік импульске ие.
кіріс дабылы барысында анықтайық: синусоидалы, бірлік секіріске және бірлік импульске ие.
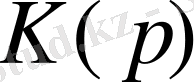 беріліс функциясы. Сызықтық төртұштықтың қасиетін n-ші дәрежелі сызықтық дифференциалды теңдеудің көмегімен анықтауға болады.
беріліс функциясы. Сызықтық төртұштықтың қасиетін n-ші дәрежелі сызықтық дифференциалды теңдеудің көмегімен анықтауға болады.
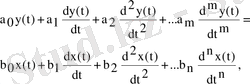 (3. 1)
(3. 1)
Мұндағы,
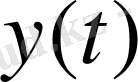 - шығыс дабылы;
- шығыс дабылы;
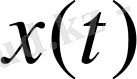 - кіріс.
- кіріс.
Сызықтық буындарды операциялық әдіспен талдау барысында Лаплас-Карсон түрлендіруі қолданылады.
Оған сәйкес (3. 1) теңдігі операциялық формада келесі түрге ие болады:
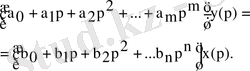 (3. 2)
(3. 2)
Шығыс дабыл бейнесінің кіріс дабыл бейнесіне қатынасына тең болатын құрылғының беріліс функциясы үшін (3. 2) теңдігі келесі түрге ие болады:
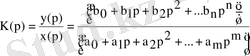 (3. 3)
(3. 3)
Немесе алымы мен мен бөлімін көбейткіштерге жіктесек (
 )
)
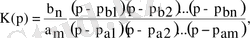 (3. 4)
(3. 4)
мұндағы
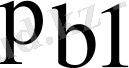 ,
,
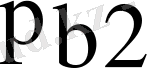 ,
,
 ,
,
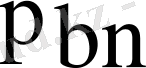 -
-
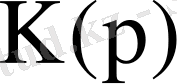 беріліс функциясының нөлдері деп аталатын
беріліс функциясының нөлдері деп аталатын
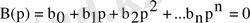 теңдеуінің түбірлері;
теңдеуінің түбірлері;
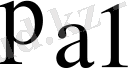 ,
,
 ,
,
 ,
,
 -
-
 беріліс функциясының полюстері деп аталатын
беріліс функциясының полюстері деп аталатын
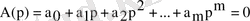 теңдеудің түбірлері.
теңдеудің түбірлері.
Орнықты жүйеде, яғни автотербеліс режиміне өтпейтін жүйеде,
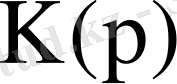 операторының барлық полюстері
операторының барлық полюстері
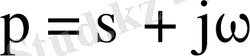 комплексті айнымалының жартыжазықтығының сол жағында орналасады, яғни барлық полюстердің нақты бөлігі
комплексті айнымалының жартыжазықтығының сол жағында орналасады, яғни барлық полюстердің нақты бөлігі
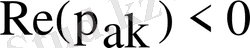 , мұнда
, мұнда
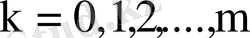 .
.
3. 3
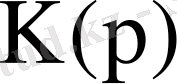 тарату коэффициенті. Фурьенің тура түрлендіруіне сәйкес кіріс
тарату коэффициенті. Фурьенің тура түрлендіруіне сәйкес кіріс
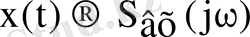 және шығыс
және шығыс
 дабылдарының спектральді тығыздықтарын анықтайық.
дабылдарының спектральді тығыздықтарын анықтайық.
Бұл спектральді тығыздықтардың қатынасы буынның тарату коэффициентінің дәл өзі
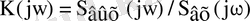 (3. 5)
(3. 5)
 шамасын Фурье интегралы Лаплас түрлендіруінің жеке жағдайы екендігін негізге ала отырып,
шамасын Фурье интегралы Лаплас түрлендіруінің жеке жағдайы екендігін негізге ала отырып,
 барысында қарапайымырақ жолмен табуға болады.
барысында қарапайымырақ жолмен табуға болады.
Сондықтан
 алмастыру арқылы беріліс функциясы (3. 5) арқылы буынды тарату коэффициентінің комплексті шамасын аламыз
алмастыру арқылы беріліс функциясы (3. 5) арқылы буынды тарату коэффициентінің комплексті шамасын аламыз
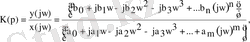 (3. 6)
(3. 6)
(3. 6) өрнегін келесі түрге келтірейік:
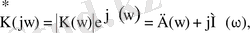 (3. 7)
(3. 7)
мұндағы тарату коэффициентінің модулі келесі формула бойынша анықталады
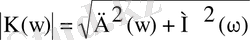 (3. 8)
(3. 8)
тарарту коэффициентінің фазасы
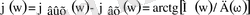 (3. 9)
(3. 9)
мұндағы
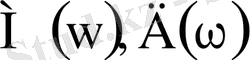 - тарату коэффициентінің нақты және жорамал бөліктері.
- тарату коэффициентінің нақты және жорамал бөліктері.
Тарату коэффициентінің көмегімен сызықтық буынның жиіліктік және уақыттық сипаттамаларын анықтауға болады.
3. 4 Амплитудалы-жиіліктік сипаттама (АЖС) дегеніміз шығыс дабыл амплитудасының тұрақты амлитуда мәніне ие кіріс дабылының жиілігіне тәуелділігі. АЖС (3. 6) өрнегіне сәйкес анықталған тарату коэффициентінің комплексті шамасының модулі болып табылады.
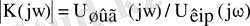 (3. 10)
(3. 10)
3. 5 Фаза-жиіліктік сипаттама (ФЖС) дегеніміз шығыс дабыл фазасының тұрақты амплитудаға ие кіріс дабыл фазасына тәуелділігі. ФЖС - бұл (3. 9) өрнегіне сәйкес анықталған тарату коэффициентінің комплексті шамасының аргументі.
Тәжірибе жүзінде АЖС мен ФЖС анықтау кезінде
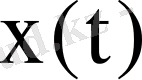 кіріс дабылы гармоникалық дабыл ретінде алынады.
кіріс дабылы гармоникалық дабыл ретінде алынады.
3. 6 Ауысу сипаттамасы
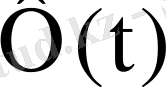 дегеніміз
дегеніміз
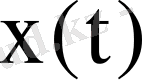 кіріс дабылы бірлік функция - кернеу секірісі - ретінде берілгендегі
кіріс дабылы бірлік функция - кернеу секірісі - ретінде берілгендегі
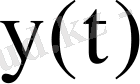 шығыс дабылының тәуелділігі:
шығыс дабылының тәуелділігі:
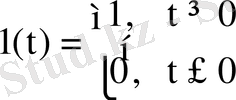 (3. 11)
(3. 11)
3. 7 Бірлік функцияның бейнесі
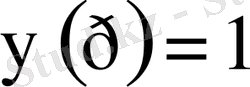 .
.
 басқа, барлық жиіліктері үшін спектральді функция
басқа, барлық жиіліктері үшін спектральді функция
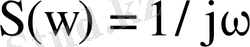 . Ал
. Ал
 болғанда,
болғанда,
 , яғни дельта-функциясына тең.
, яғни дельта-функциясына тең.
Уақыттық сипаттама үшін тәуелділікті табуды
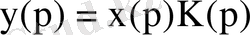 шығыс дабылдың бейнесі арқылы жүзеге асыруға болады. Лаплас-карсон түрлендіруіне сәйкес, бірлік функцияның бейнесі
шығыс дабылдың бейнесі арқылы жүзеге асыруға болады. Лаплас-карсон түрлендіруіне сәйкес, бірлік функцияның бейнесі
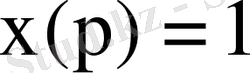 болғандықтан, ауысу сипаттамасы - беріліс функциясының түпнұсқасы:
болғандықтан, ауысу сипаттамасы - беріліс функциясының түпнұсқасы:
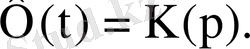 функцияның бейнесі арқылы түпнұсқаны табу жіктеу формуласымен операциялық есептеулер жүргізу арқылы жүзеге асады. Ол үшін беріліс функциясының полюстерін, (3. 4) өрнегіне сәйкес теңдеудің нақты және комплексті түбірлерін табу қажет.
функцияның бейнесі арқылы түпнұсқаны табу жіктеу формуласымен операциялық есептеулер жүргізу арқылы жүзеге асады. Ол үшін беріліс функциясының полюстерін, (3. 4) өрнегіне сәйкес теңдеудің нақты және комплексті түбірлерін табу қажет.
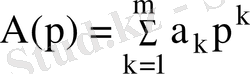 (3. 12)
(3. 12)
Нақты коэффициенттері бар полиномның (3. 12) нақты және комплексті түбірлерін табудың бірнеше сандық әдістері белгілі. Олардың бірі Ньютон-Рафсон әдісі. Осы тәріздес есептерді Mathcad бағдарламасының математикалық пакеті арқылы жүзеге асыруға болады.
Ауысу сипаттамасын есептеудің басқа әдісі беріліс функциясының (3. 3) өрнегінен шығады және полиномның (3. 12) түбірлерін алдын-ала табуды талап етпейді.
Тізбектің орнықтылық шарттарын
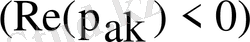 жүргізу барысында және
жүргізу барысында және
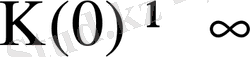 болғандағы Фурье интегралының Лаплас түрлендіруімен байланысына және интеграл асты функциясының интегралдану шарттарына қайта негізделе отырып, тізбектің ауыспалы сипаттамасы үшін дәл сол объектінің
болғандағы Фурье интегралының Лаплас түрлендіруімен байланысына және интеграл асты функциясының интегралдану шарттарына қайта негізделе отырып, тізбектің ауыспалы сипаттамасы үшін дәл сол объектінің
 (3. 7) тарату коэффициентінің
(3. 7) тарату коэффициентінің
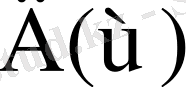 нақты бөлігі арқылы берілген келесі өрнекке қол жетуізуге болады.
нақты бөлігі арқылы берілген келесі өрнекке қол жетуізуге болады.
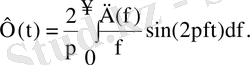 (3. 13)
(3. 13)
3. 8 Импульсті сипаттама дегеніміз
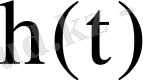 бірлік импульс немесе бірлік функциясының (3. 11) туындысы - дельта-функция
бірлік импульс немесе бірлік функциясының (3. 11) туындысы - дельта-функция
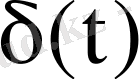 түріндегі
түріндегі
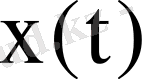 кіріс әсеріне объектінің үндеуі
кіріс әсеріне объектінің үндеуі
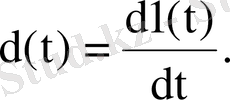 (3. 14)
(3. 14)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz