Эль-гамаль цифрлық қолтаңба программалық өнімін құрастыру

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 50 бет
Таңдаулыға:

Кіріспе

Криптография ғылымы ежелгі заманғы ғылым. Криптографияны құпияны сақтау үшін қолданады. Қазіргі заманғы ақпараттық технологиялардың қарқынды дамуына байланысты, сонымен қатар өмірлік циклдің барлық салаларында электронды ақпараттардың көптеп қолданылуымен бірге оларды қорғау мәселесі туындайды. Криптографиялық қорғау құралдары дегеніміз - мәліметтерді шифрлау әдісі, яғни арнаулы мәліметтерді қолдану арқылы мәліметтерді қорғау әдісі, яғни электронды есептеуіш машинасында сақталған мәліметтерді заңсыз пайдаланудан шифрлау әдісін қолданып қорғау. Заман талабына сай қазіргі барлық ірі және кіші кәсіпорындардың ішкі ақпараттарының барлық түрі автоматтандырылған құжаттандыру жүйесіне көшуіне байланысты цифрлық қолтаңбалардың қажеттігі туындап отыр. Криптологияның негізгі әдістерінің бірі электронды цифрлы қолтаңба болып табылады. Электронды цифрлы қолтаңбаны іске асыру алгоритмдерінде қолданылатын математикалық кестелер біржақты функцияларға негізделеді.

Дипломдық жобаның мақсаты - құжаттың нақты екендігін және алушының-жіберушінің өздері екендігін анықтау, яғни құжаттарды аудентификациялау.

Бұл дипломдық жобаның құрылымы кіріспеден, негізгі бөлім, арнаулы бөлім, бағдарламаны сипаттау, экономикалық тиімділік, еңбекті қорғау, қорытынды және қосымшадан тұрады.

Бірінші бөлімде ашықкілтті криптожүйелер туралы кірісті ақпараттар беріледі.

Екінші бөлімде электроды цифрлы қолтаңбаны қолданудың компьютерлік технологиясы туралы жазылған.

Ал үшінші бөлімде бағдарлама жұмысына түсінік берілген

Төртінші, бесінші бөлімдерде экономикалық тиімділік, техникалық қауіпсіздік және еңбек қорғау туралы жазылған.

1. Ашықкілтті криптожүйелер

1. 1. Біржақты функциялар

Шеннонның жұмысынан, біріншіден, тұрақты құпия жүйелерде қолайсыз үлкен көлемдегі кілттердің қорғалған каналы бойынша берілуі талап етіледі. Екіншіден, тәжірибелі тұрақтылық сұрағына шешімнің жаңадан пайда болуынан гөрі, криптологиялық тәсілдері бар жылдам жетілдіру сәйкес келеді. Бірақ, «жақсы шифр құру проблемасы болып, белгілі бір жағдайды қанағаттандыратын, көп аса қиын тапсырмаларды табу проблемасы табылады … Шифрды мынадай жолмен ашуға болады, кейбір проблемалардың шешімі болатындай, шифрды ашу эквиваленті болсын, ал оның шешілуі үшін үлкен көлемді жұмыс қажет», -деген Шеннонның ескертпесі, стэндфордалық оқымыстылар У. Диффи мен М. Е. Хеллманның толғаныстарында пікір тапты. Олардың баптары 1975 жылы жарияланған, құпия кілттің табысталуын талап етпейтін тұрақты құпия жүйесін құруы мүмкін деген хабарламамен мазмұндалған.

Олардың шешуші жинақтары екі өте қысқа анықтамамен қорытыланған: «Біржақты функция» және жаңа «жасырын жүрісті біржақты функция».

Біржақты функция дегеніміз - бұл анықтама бойынша, кейбір 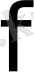функциясы кез-келген үшін, оның анықталу облысынан 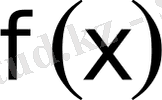есептелінген; бірақ барлық үшін мәндер облысынан табылуы, 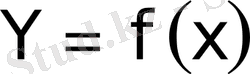үшін, есептеу жүзеге аспайды. Бұл анықтама математикалық дәлдік болмайды.

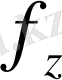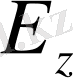Жасырын жүрісті біржақты функция бар, ол, параметрімен анықтама бойынша қайтымды функция; берілгенімен және 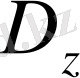алгоритмдерін табуға болады, анықьалу облысынан барлық X үшін Fz(X) және мәндер облысынан барлық Y үшін 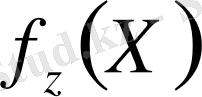қатыстарын жеңіл есептеуге болады; бірақ барлық Z үшін және мәндер облысынан барлық Y үшін 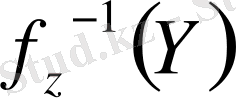табылуында есептелінеді. Осы анықтама математикалық дәлдік болмайды, бірақ оны криптографияда қолданылатындығы айқын.

1. 2. Кілттердің ашық таратылуы

Диффи мен Хеллман біржақты функцияның мүмкін болатын сапасында дискретті тұрғызу функциясын мына деңгейде ұсынды:

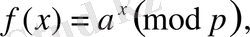
мұнда, X- 1-ден p-1-ге дейінгі бүтін сан, ал есептеу p модулі бойынша жүреді, мұндағы, p-өте үлкен қарапайым сан;

а- бүтін сан (1≤а≤p),

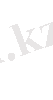
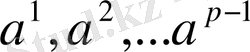-ді 1, 2, …, р-1-ге тең болады.

Мысалы, р=7 болғанда, 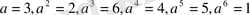теңдігінен a=3- ті таңдауға болады. Егер 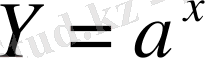тең болса, онда

болады, ал, 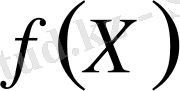айналу функциясын дискреттік логарифмдерді табу тапсырмасы деп атауға болады. Р өте үлкен болғанда да, яғни 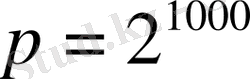деп алсақ, онда 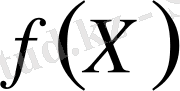функциясын квадрат және көбейту жолымен жеңіл есептелінеді. Мысалы, 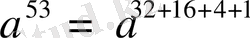теңдеуін есептеу үшін, алдымен 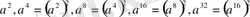табу керек, ол үшін көбейтудің бес операциясы қажет. Одан кейін 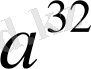дәрежесі көбейтіледі, осы жолмен сегіз операцияда нәтиже алынады. 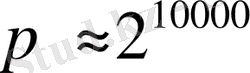кез-келген 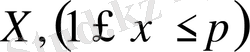бүтін сан үшін 2000-нан кем көбейту операциясы қажет (р модулі бойынша) .

Егер дискретті тұрғызу деңгейдегі функция біржақты болса, онда 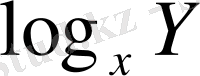есептелінуі барлық Y, (1≤Y≤p) үшін орындалмауы керек. Хеллман мен Полиг р үлкен болу жағдайында дискреттік логарифмдердің қиын есептелетіндігін тапты. Егер дискреттік логарифмдер функциясын есептеу шын мәнінде қиын болса, онда көрсетілген шекте 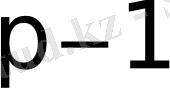біржақты болып табылады. Бірақ бұл қатаң түрде дәлелденбеген.

Тек ашық хабарламаны қолдануымен ғана желіні пайдаланушылар арасындағы құпия кілттерді ауыстыру үшін Диффи мен Хеллман дискреттік логарифмдерді қолданудудың жай тәсілін ұсынды. Барлық пайдаланушыларға және белгілі деп есептейік. Әрбір пайдаланушыны орындаушы деп айтсақ, 1 мен 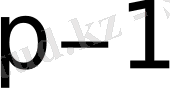арасында қорытыланған 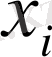бүтін санын таңдайды және оны құпияда ұстайды. Ол былай есептелінеді:

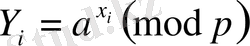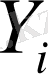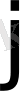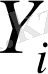Пайдаланушы - ді құпияда ұстамайды, онда барлық пайдаланушыға оңай сенімдендірілген ашық анықтамалық кедергі жасайды. Егер мен i пайдаланушылар құпия байланысты орнатқысы келсе, пайдаланушы -ді анықтамалықтан алып, өз құпиясы көмегімен есептейді:

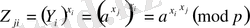Осындай жолмен j пайдаланушы -ді есептейді. Бірақ және және 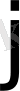пайдаланушылар осы кезден бастап, классикалық криптожүйелерде құпия кілт ретінде 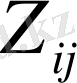-ді қолданылады. Егер қаскөй дискреттік логарифмді есептеу тапсырмасын шеше білсе, онда ол анықтамалықта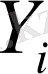н мен 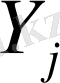-ді алып, 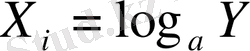теңдігін шешеді және пайдаланушы 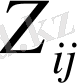-ді есептейді. Бәрін көріп отырғанымыздай, қаскөй 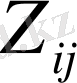-ді басқа тәсілмен анықтай алмайды. Төменде көрсетілген сызба Диффи мен Хеллманның ашық таратылатын кілт жүйесі деп аталады.

Мысал. , р=15 болсын. і пайдаланушы санын қалыптастырады, сосын 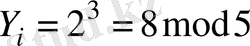есептеп, j пайдаланушыға жібереді. j пайдаланушы 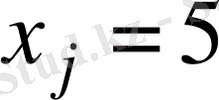қалыптастырады және 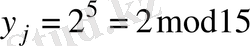-ті i пайдаланушыға жібереді. i және j пайдаланушылар есептелінуі сәйкес келеді:

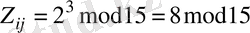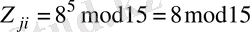
Осындай бейнеде, .

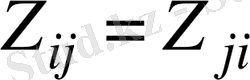Бұл құпия кілттерді берілістен бас тартатын ең бірінші жүйе, және бүгінгі күнде ашық кілтті тұрақты және қолайлы жүйе болып есептеледі.

Ашық кілттерді таратуы түсінікті жүйесі құпия кілттердің берілісі үшін қорғаусыз каналы үшін айналып өтуге болады, бірақ аутенфикацияның қажеттілігін босатпайды.

Жалпы оңай анықтамалықты сақтаушы i пайдаланушы анықтамалықта 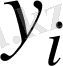құпиясыз кедергі болады, ал, i пайдаланушы 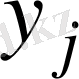анықтамалық сақтаушысы жібергенін білуі керек.

Құпиялық кілттер жүйесінде алушы кілті беріліс кезінде құпияда сақталғанына сенімді болуы керек.

1. 3 RSA және Эль-Гамаль криптожүйелері

Жасырын жүрісті біржақты функциялар анықтамасына негізделіп, Диффи мен Хеллман желі үшін көптеген пайдаланушыларымен ашық кілтті криптожүйенің құрылымын ұсынды.

Әрбір пайдаланушы, яғни i пайдалушы десек, кездейсоқ жолмен көрсеткіштің 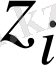мәнін таңдап, оны құпияда ұстайды. Содан кейін, ол 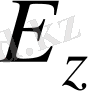алгоритмін қалыптастырады және оны ашық анықтамалықта жариялайды. Ол тағы да 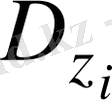алгоритмін қалыптастырып, оны да құпияда ұстайды. Егер j пайдаланушы i пайдаланушыға x құпия хабарлама жібергісі келсе, онда ол 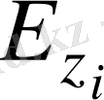алгоритмін анықтамалықтан алады және оны i пайдаланушыға жіберетін, 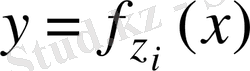криптограммасының құрылуы үшін қолданады. i пайдаланушы өзінің 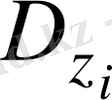құпия алгоритмін 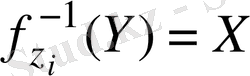есептеу үшін қолданады.

Егер 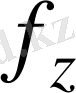шын мәнінде, жасырып жүрісті біржақты функциялар болса, онда бұл криптожүйе сөзсіз тәжірибелі тұрақтылықты қамтамасыз етеді.

Диффи мен Хеллман егер барлық көрсеткіште 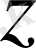анықталу облысындағы 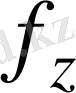функциясы оның мәндер облысымен сәйкес келеді, онда осындай біржақты функция көмегімен цифрлық жазулар алуға болады. Егер 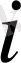пайдаланушы х құпиясыз хабарлама жібергісі келсе, онда ол 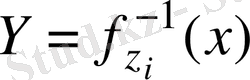алу үшін өзінің құпия алгоритмін қолданады. Әрбір пайдаланушы 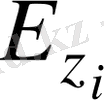ашық алгоритмін біліп, 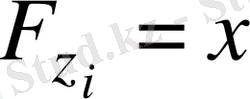-ті алады, бірақ, тек қана i пайдаланушы 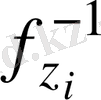-ді есептей алатындықтан, х хабарламасын i пайдаланушыдан басқалары түсіне алмайды.

Әрине, i пайдаланушы j пайдаланушыға құпия хабарлама сөзбен жібере алады; ол үшін j пайдаланушыға 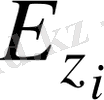ашық кілтін қолдана отырып, ол Ү-ді ашық түрде емес шифрлап жіберуі керек.

RSA криптожүйесі 1976 жылы Диффи мен Хеллман жасырын жүрісті біржақты функция бар екенін білмей тұрып, олар өз мақаларында осындай функциялардың мүмкін түрлерін көрсеткен жоқ. Алғаш рет 1978 ж. жасырып жүрісті біржақты функция ұғымын Массаrусеттік технологиялық институтта жұмыс жасайтын американ математиктері Р. Л. Ривест, А. Шамир, Л. Адыман ұсынған болатын. RSA біржақты функциясы жай қарапайым емес, бірақ оның жазылуына сандардың элементарлық теориясынан кейбір мағлұматтарды қажет етеді:

ЕУОБ(i, n) i және n бүтін сандарының ең үлкен ортақ бөлгішін білдіреді, олар бір уақытта нөлге тең емес.

р жай саны үшін, 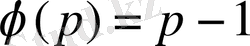болады; р және q екі тең емес жай сандар үшін мынаны байқау қиын емес:

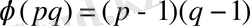
Мысалы, 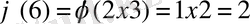. Белгілі Эйлер теориясынды: ЕУОБ(Х, n) =1 тең болған жағдайды. х және n(X, n) кез-келген бүтін саны үшін

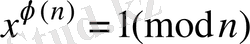
болатындығын хабарлайды.

Сандар теориясынан бізге қажетті дәлел Евклидке өршиді. Егер ЕУОБ(n, е) =1, 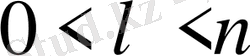жағдайын е және қанағаттандырса, онда жалғыз 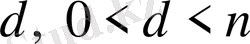бар,

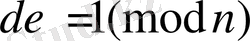және ЕУОБ(n, е) табу үшін, Евклидтің “ұлғаю” алгоритм көмегімен 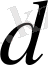есептелінуі мүмкін.

Жасырын жүрісті RSA біржақты функциясымен жай дискреттік дәрежесін шығару бар:

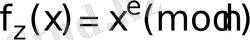мұндағы, х- оң бүтін болмайтын, 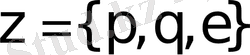, "жасырын жүріс", және - үлкен тең емес сан; ал,

е - ЕУОБ 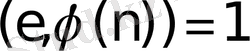үшін 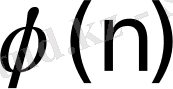болмайтын оң бүтін сан.

алгоритмі 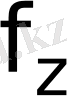жылдам есептелуі үшін оңай табылады: бұл жай квадраттау және көбейту тәсілі; бұл алгоритмнің жариялымы және е мәндерінің жариялымына сәйкес келеді.

Кері функцияның мынандай түрі бар:

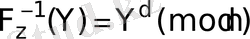мұндағы 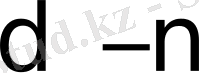- нен піші, жалғыз оң бүтін және мына жағдайды қанағаттандырады:

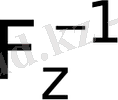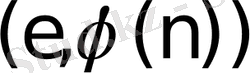есептеу үшін алгоритмі оңай табылады: бұл да квадраттау және көбейтуді шығару тәсілі, шифрды ашуда қажет көрсеткіші ЕУОБ есептелінетін Евклид алгоритмі көмегімен табылады.

Сол дәлел функция шын мәнінде функция болып табылатындығы, кері функцияға келесі жолмен көрсетіледі. Жай бүтін сандық арифметикада теңдігі кейбір

-ге эквивалентті:

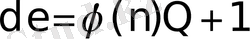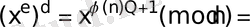
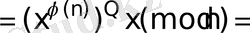
мұндағы соңғы теңдікте Эйлер теоремасы қолданылған. Теңдігі, е дәрежесін шығару операциясының қатынасы бойынша дәрежесіне санды шығару операциясы кері екендігін көрсетеді.

1. 4 RSA крипжүйесінің сызбасы

"НАЗ" хабарламасын шифрлауын келтірейік. Қарапайымдылық үшін өте кішкентай сандарды қолданатын боламыз.

және-деп аламыз.
анықтаймыз.
Equation. 3 табамыз да, Equation. 3 ретінде өзара жай болатын кез-келген санды аламыз, мысалы, Equation. 3 .
е санын аламыз. Бұндай сан ретіндеEquation. 3 қатысын қанағаттандыратын кез-келген сан алынады, мысалы 7.
Шифрланатын хабарламаны (0…32) өрісіндегі бүтін санның тізбектелуі ретінде көрсетеміз. А әрпі 1 санымен, 3 әрпі 8 санымен, Н әрпі 14 санымен белгіленсін.

Онда хабарламаны 14 1 8 тізбеутей сандар түрінде көрсетуге болады. Хабарламаны кілтін қолдана отырып, шифрлаймыз:

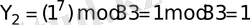
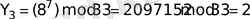хабарламасының шифрын ашуға тырысайық, олқұпия кілті негізінде, белгілі кілт бойынша:

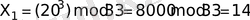
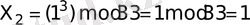
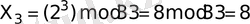Осындай әдіспен хабарламаны шифрдын ашу нәтижесінде "НАЗ" нәтижелі хабарламасы алынды.

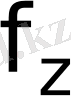айналу функциясы білім негізінде тек және е есептелінуі іске аспайтындығын және қаской шеше алмайтын жолмен екі үлкен тең емес және жай сандарды кездейсоқ таңдауға болады деп авторлардың санағанын көрсетейік.

Қаскойге тек Equation. 3 мен е ғана белгілі. Бірақ, Equation. 3 -ді көбейткішке жіктеп, ол 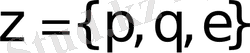Equation. 3 "жасырын жүріс" туралы толық ықпараттары бар, және де заңды алушы ретінде хабарламаны шифрды жеңіл ашады. RSA криптожүйесінің тұрақтылығы 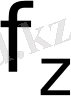Equation. 3 айналу функциясының кез-келген тәсілі Equation. 3 көбейткішіне жіктелуіне эквивалентті босатылуына негізделген.

Equation. 3 көбейткішіне жіктелуінің есептелінуі жүзеге аспайтындығы дұрыс па? Жауап болады, егер таңдалған Equation. 3 мен Equation. 3 ұзындылығы 150-200-ге жуық ондық мәнді құраса, онда көбейткішке жіктеу облысында революциялық сілкініс болмайды.

Соңғы жиырма жылда есептегіш техника қатты қамыған кезде және факторизация тапсырмасында көптеген мамандар күші ортақталған кезде, факторизация тиімділігі айтарлықтай өсті.

Сандардың факторизациясы үшін есептеу жұмысын мипсогод есептеуге болады (MIPS - Million Instructions Per Second - секундына миллион команда) . Осындай жолмен, мипсогод - секундына 1 миллион операция тезәрекетпен орындайтын машина операциясының саны. Осы уақытта ол 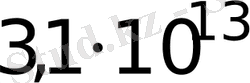жуық операция орындайды. 1983 жылы рекорд 0, 1 мипсогодты қажет етті, ал 1994 жылы - 5000 мипсолет.

1990 жылы жаңа жұмыстар табылды, GNFS (Genral Number Ficld Siwe - жалпы сандық алаңы шешілген) - криптографияда қолданылатын мөлшердегі сан үшін қолданылады. Қазір, GNFS сандарды факторизациялау үшін, 110 санынан бастап, табысты қолданылады.

GNFS алгоритмнің факторизациясы.

Басқа жағынан, компьютер қуаты тез өсіп келеді, ал олардың бағасы әлдеқайда жай өседі.

Р. Л. Ривест математикалық/программалық қамтамасыз етуде (Software) және аппараттық бөлімде (hardware) прогресс жиынын келесі көлемдермен (процентті/жыл) бағалады:

пессимистикалық баға (пб) - 20;

орташа баға (об) - 33;

оптимистикалық баға (об) - 45.

Содан кейін, Р. Л. Риверст қазір 1 долларға қанша мипсолет сатып алуға болатындығын бағалайды: 500 долларға 10 тез әрекетті құрастырмалы машинаға 10 мипс. Сатып алады. Ал ол машина 5 жыл жұмыс жасайды.

Р. Л. Ривест индивидуум корпорация және мемлекет шифрды ашу үшін қанша жұмсайтындығын көрсетеді.

индивидуум - 25 мың доллар;

корпорация - 25 млн доллар;

мемлекет - 25 млрд доллар.

Кілттерді ашудың барлық тәсілдері көп компьютерлерді параллельді пайдалануды жібереді. 129 - мәнде сан туралы қысқаша айтайық. 1977 ж. белгілі математик Мартин Гарднер Scietific American- ға шифрды ашу үшін 129 мәнді санды көбейткішке жіктеу керек шифрын жариялады.

N=11 43 81 62 57 57 88 88 67 66 92 35 77 99 76 14 66 10 01 02 18 29 67

21 24 36 25 62 56 18 42 93 57 06 93 52 45 73 38 97 83 05 97 12 35

63 95 87 05 0589890 7514 75 99 29 00 26 879543541

1600 машина қатысады, қарапайым персональды компьютерден бастап. Gray C90 станциясына дейінгі, уақытша "суперкомпьютер" ұйымдастырылған. 5000-ға жуық мипсолет қажет ететін тапсырма нәтижесінде 1993 жылдың тамызынан 1994 жылдың сәуіріне дейін шешілген болатын. Принцип бойынша Internet барлық машиналары N-ді 3 сағатта факторизациялауға болатындығын, -авторлар ескереді.

Қызығы дискреттік логарифм тапсырмасын шешуінің белгілі алгоритмдері және көбейткішке жіктеу алгоритмдері, болғанда, есептеудің жуық бірдей санын талап етеді; сондықтан, Диффи мен Хеллман функциясы және RSA функциясы бүгінгі күнде тең негізде "бір жақты" деп аталады.

1. 5 Эль-Гамаль криптожүйесі

GF(q) алаңында Эль-Гамаль жүйесін сипаттаймыз; мұндағы, негізді немесе негізді деңгейі (бұнда ) ; - алаңның бірінші бейнелі элементі.

А пайдаланушының - құпия кілті болсын және ашық кілт, осыған ұқсас, В - пайдаланушының в -құпия кілті, ал 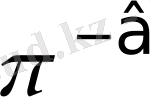- ашық кілт. В пайдаланушыға М құпия хабарлама жіберу шін, А пайдаланушы кездейсоқ бүтін санды таңдайды және 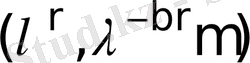-жұбын жібереді. Бұнда, - разрядты көрсетудегі М көрсетілім. Егер А пайдаланушы таңдалған кілт болып М табылса, онда ол кілттік ауыстыру механизмі ретінде жарамды болады.

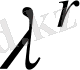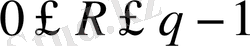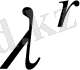В пайдаланушыға М жазылған хабарламаны жiбере отырып, А пайдаланушы тағы n кездейсоқ бүтiн санды таңдайды және -дi есептейдi. Толық R, ( ) мен көрсетiлiмi болады. Ал, А пайдаланушы

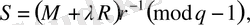
есептеп, М хабарламасын 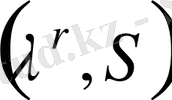жазуымен бiрге жiбередi.

1. 6. Асимметриялық криптожүйелердiң салыстырмалы талдауы

Факторизация тапсырмасын шешу үшiн квадраттық негiзде анықталған алгоритмдер шешiледi. Салыстыру нәтижесi Эль-Гамаль криптожүйесiмен RSA криптожүйсiнiң арасындағы тәжiрибедегi қиындығын салыстыру үшiн қолданылады.

RSA мен Эль-Гамаль криптожүйелерiнiң тұрақтылығы дискреттiк логарифмдердiң есептелуi мен факторизация қиындығының қатынасына эквиваленттi болады, мұндағы

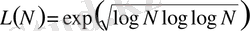
Теория жүзiндегi бағаға С константа кiредi. Олдрижко жетiлдiруiмен Купершмид алгоритмi 32-разрядты мантиссалы компьютер үшiн 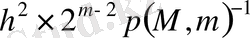жылжуын және қосуын талап етедi. Мұндағы,

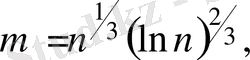
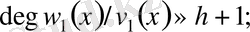
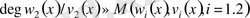Equation. 3,

Бұлар алгоритмнiң бiрiншi кезеңiнде қолданылатын көпмүшелiктер.

Квадраттық шешiмдегi алгоритмнiң элементарлық операция саны мына өлшемде бағаланады:

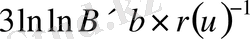Equation. 3,

мұндағы в- 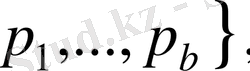Equation. 3 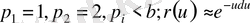Equation. 3

2. Электронды цифрлы қолтаңба

2. 1. Құжаттарды аутентификациялау

Қағазсыз информатика байланыс желілері немесе машиналық тасымалдауыштар арқылы құжаттармен (бұйрықтармен, хаттармен және т. с. с. ) айырбас жасау кезінде көптеген артықшылықтар береді. Бұл жағдайда уақытша шығындар (құжатты баспаға шығару, қайта жіберу, алынған құжатты перне тақтамен енгізу) көп есе азаяды, құжаттарды іздеу жылдамдайды, оларды сақтау шығындары азаяды және т. с. с. Бірақ бұл кезде құжаттың авторын және құжаттың өзін аутентификациялау қиындығы пайда болады (яғни қолтаңбаның ақиқаттығын және алынған құжатта өзгеріс жоқ екендігін анықтау) . Бұл қиындықтар кәдімгі (қағаздық) информатикада, құжаттағы ақпарат және тұлғамен (қағазбен) тығыз байланысты болғандықтан оңай шешіледі. Машиналық тасымалдағыштарда мұндай байланыс жоқ.

Аутентификациялау қиындығы есептегіш желілерде, электронды басқару жүйелерінде және жалпы, байланыс каналдары немесе машиналық тасымалдауыштар арқылы алынған хабарламаның (құжаттың) ақиқаттығын анықтау кезінде өзекті болып табылады.

Аутентификациялау мәселелерін келесі түрлерге бөлуге болады: қолданушы аутентификациялау, қолданушының берілген топқа сай екендігін аутентификациялау, машиналық тасымалдауыштарда сақтаулы құжаттарды аутентификациялау.

Ең маңыздысы ретінде құжаттарды (немесе файылдарды) аутентификациялауға тоқтаймыз. Егер құпиялы құжаттармен айырбас жасау жағдайы қарастырылса (әскери немесе дипломатиялық байланыс), онда айырбас жасау сенімді және сенімге сай жақтар арасында жүзеге асырылатындығын жоғары дәрежелі сенімділікпен болжауға болады. Бірақ айырбас жасау, қиын есептеулер жүргізе алатын қаскүнемнің бақылауында және басқаруында болуы мүмкін, кейіннен ол өзінің құжаттарын жасауы немесе заңды жіберушінің құжатын ұстап алып оны өзгертуі мүмкін. Басқа сөзбен айтқанда, бұл тек қаскүнемнен қорғану керек жағдай - “өзіміздікі” алдай алмайды. Коммерциялық әлемде бұл жағдай керісінше болуы мүмкін, яғни жіберуші мен алушы “өздерінікі” болғанымен, басқаларға қарағанда бір-бірін көп дәрежеде алдауы да мүмкін.

Бірінші жағдайда (“өздерінікі алдамайды”) аутентификациялау кестесін құру қиын емес. Жіберуші мен алушы қолданушыларды сенімді шифрмен және әрбір жіберілетін құжат үшін сапалы кілттер комплектісімен жабдықтау арқылы, қорғалған байланыс каналын қамтамасыз етеміз. Қарастырылып отырған мәселе шифрлау жүйесіне жоғары талаптар қоятынын айтып кетейік. Айталық гаммирлау әдісі бұл жағдайда қолдануға келмейді, себебі қаскүнем ашық және жабық мәтінді талдап гамманы алады да, кез-келген өзіне керек мәтінді тіркеп жібере алады. Алайда қойылған талаптарды қанағаттандыратын жылдам шифрлау алгоритмдері бар.

Екінші жағдайда (“қолданушылардың кез-келгені алдауы мүмкін болғанда”) классикалық криптографияға негізделген әдісті қолдана аламыз, себебі құпиялы кілті бар бір жақ зиянды әрекеттер жасауына принципиальды мүмкіндік бар. Мысалы, алушы жақ кез-келген құжатты генерациялап өзіндегі алушыға да, жіберушіге де ортақ кілтпен шифрлап, сосын ол құжатты заңды жіберушіден алдым деуі мүмкін. Бұл жерде екі кілтті криптографияда негізделген кестені қолдану керек. Бұл жағдайда жіберушіде өзінің құпилы кілті болады, ал алушыда жіберушінің құпиялы кілті болады. Бұл ашық кілтпен жіберушінің қолтаңбасының ақиқаттығын тексеруге болады да, ол арқылы құпиялы кілтті шығарып алуға болмайды. Жіберуші өзінің жабық кілтіне жеке жауапкершілік білдіреді. Одан басқа ешкім корректілі қолтаңбаны генерациялай алмайды. Құпиялы кілтті жіберушінің жеке мөрі ретінде қарастыруға болады, сондықтан кілттің иесі басқа тұлғалардың оған қол жеткізуін шектеуі керек.

Құжаттарды аутентификациялаудың негізгі мақсаты әртүрлі мүмкін қаскүнем әрекеттерден қорғау, солардың ішінен бөліп көрсетейік:

Активті ұстап алу - қаскүнем желіге жалғанып алып құжаттарды (файлдарды) ұстап алады және оларды өзгертеді;
Маскарад - С құжатты А атынан жібереді;
Ренегаттылық - А хабарламаны В-ға жібергенімен жіберген жоқпын деп мәлімдейді;
Өзгерту - В құжатты өзгертеді де, сол құжатты (өзгертілген) А-дан алдым деп мәлімдейді;
Ауыстыру - В құжат (жаңа) жасайды да, оны А-дан алдым деп мәлімдейді;
Қайталау - А-ның В-ға бұрын жіберген құжатын С қайталап жібереді.

Бұл қаскүнем әрекеттердің түрлері, өз қызметінде компьютерлік ақпараттық технологиялар қолданатын банктердің, коммерциялық құрылымдардың, мемлекеттік кәсіпорындардың және ұйымдардың, жеке тұлғалардың қалыптасуына маңызды залаларын тигізеді. Сондықтан қаскүнем әрекеттер жасау мүмкіншілігі, компьютерлік технологияларға сенімділікті кеміте түсіреді. Осыған байланысты аутентификациялау мәселесі маңызды болып келеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.