Delphi ортасында бір айнымалы функцияларды зерттеу: математикалық теория мен программалау


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . 3
I Бір айнымалы функцияларды зерттеудің математикалық теориясы . . . 5
1. 1 Бір айнымалы функциялардың негізгі қасиеттері . . . 5
1. 2 Бір айнымалы функцияларды зерттеу . . . 12
II Delphi ортасында функцияларды зерттеу алгоритмдерін программалау . . . 23
2. 1 Декарт координат жүйесінде функцияның графигін салу . . . 25
2. 2 Функция графиктерін түрлендіру . . . 30
2. 3 Поляр координат жүйесінде функцияның графигін салу . . . 32
Қорытынды . . . 35
Пайдаланылған әдебиеттер . . . 36
Кіріспе
Функция - математиканың негізгі ұғымдарының бірі. Әртүрлі физикалық, экономикалық, әлеуметтік процесстердің өзгеріс заңдылығының сипаттамасы. Бұл заңдылықтың математикалық моделдері функция түрінде болады. Курстық жобада бір айнымалының функциясын зерттеу әдістемесі қарастырылған. Бұл тақырыпта зерттеу жұмысын жүргізу мынадай қажеттіліктерден туындайды: біріншіден мұғалімге функцияны зерттеу тақырыбына электрондық әдістелік құралдың қажеттілігі; екіншіден функцияның графигін (милиметрлік қағазсыз) дәл әрі нақты түрде салудың қажеттілігі; үшіншіден, математикалық зерттеу жұмысын компьютер көмегімен жеңілдету; төртіншіден, математикада көп қарастырылмайтын стандартты емес функцияларды графигі арқылы толық зерттеу.
Жоба үш бөлімнен тұрады. Бірінші бөлімде декарт координат жүйесінде берілген кейбір функцияларды зерттеу әдістемесі қарастырылған. Екінші бөлімінде элементар түрлендірулер көмегімен графиктерді түрлендіру арқылы зерттеу қарастырылған. Үшінші бөлімде поляр координат жүйесінде берілген кейбір функциялардың графиктерін зерттеу әдістемесі қарастырылған.
Мақсаты: Delphi ортасында бір айнымалының функциясын зерттеу әдістемесін жасау.
Зерттеу объектісі : математикалық функциялар
Бағыты : оқыту - әдістемелік
Жұмыс барысы : Курстық жоба екі тараудан тұрады. Бірінші тарауда бір айнымалының функциясын зерттеудің математикалық теориясы қарастырылады. Негізгі элементар функциялар, олардың сипаттамасы: анықталу облысы, өсу кему аралықтары, экстремумдары, графигін тұрғызу, т. б. жалпы алғанда функцияны толық зерттеу схемасы қарастырылады.
Екінші тарауда қосымша құрылған орта туралы айтылады. Delphi ортасында функцияны зерттеу әдістемесі құрылған. Жоба үш бөлімнен тұрады. Бірінші бөлімде декарт координат жүйесінде берілген кейбір функцияларды зерттеу әдістемесі қарастырылған. Бұл бөлім кез келген функцияны графигі арқылы зерттеуге мүмкіндік береді. Математикалық анализдің кейбір сирек қарастырылатын функцияларын зерттеуге болады. Ондай функциялардың кейбіреулері 2. 1 бөлімде қарастырылған. Екінші бөлімде элементар түрлендірулер көмегімен графиктерді түрлендіру арқылы зерттеу қарастырылған. Осы тақырыпты 8-класстың математика оқулығына қарастырылады. Сол сабақты түсіндіргенде оқытушыға осы құралды пайдалануға болады. Үшінші бөлімде поляр координат жүйесінде берілген кейбір функциялардың графиктерін зерттеу әдістемесі қарастырылған. Жалпы поляр координат жүйесі туралы әдістемелік құралдар өте аз кездеседі.
Қолданылуы : Бұл курстық жобадық жұмысты мектепте, жоғары оқу орындарында «Функцияны зерттеу» тақырыбын оқытқан кезде әдістемелік құрал ретінде пайдалануға болады.
I Бір айнымалы функцияларды зерттеудің математикалық теориясы
1. 1 Бір айнымалы функциялардың негізгі қасиеттері
Негізгі түсініктер
Кез келген парлар жиыны қатынас деп аталады. Парлардың бірінші элементар жиыны қатынастың анықталу облысы деп, ал элементер жиыны оның мәндер облысы деп аталады. Егер қатынастың анықталу облысы
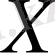 жиындарының бөлігі, ал мәндер облысы
жиындарының бөлігі, ал мәндер облысы
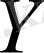 жиынының бөлігі болса, ондай қатынас
жиынының бөлігі болса, ондай қатынас
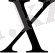 және
және
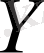 жиындары элементтерінің арасындағы қатынас деп аталады.
жиындары элементтерінің арасындағы қатынас деп аталады.
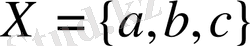 және
және
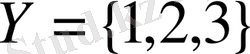 жиындарының арасындағы
жиындарының арасындағы
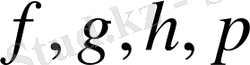 қатынастар 1-суретте бейнеленіп көрсетілген. Бірінші элементері өзара тең емес парлардан тұратын
қатынас функция
деп аталады.
қатынастар 1-суретте бейнеленіп көрсетілген. Бірінші элементері өзара тең емес парлардан тұратын
қатынас функция
деп аталады.
Мысалы,
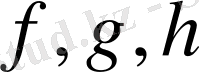 қатынастары функция болып табылады, ал
қатынастары функция болып табылады, ал
 қатынасы функция бола алмайды, өйткені оған бірінші элементтері бірдей
қатынасы функция бола алмайды, өйткені оған бірінші элементтері бірдей
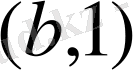 және
және
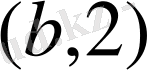 екі пар еніп отыр. Егер
екі пар еніп отыр. Егер
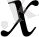 элементі
элементі
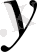 элементімен берілген қатынас түрінде байланысса, онда
элементімен берілген қатынас түрінде байланысса, онда
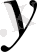 элементі
элементі
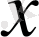 элементіне сәйкес келеді дейді. Демек, функция дегеніміз анықталу облысының әрбір элементіне мәндер облысының бір ғана элементі сәйкес келетін қатынас болады. Жеке жағдайда,
элементіне сәйкес келеді дейді. Демек, функция дегеніміз анықталу облысының әрбір элементіне мәндер облысының бір ғана элементі сәйкес келетін қатынас болады. Жеке жағдайда,
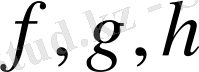 қатынастары үшін
қатынастары үшін
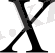 жиынының әрбір элементіне
жиынының әрбір элементіне
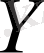 жиынының бір ғана элементі сәйкес келеді, не ешбір элементі сәйкес келмейді. Енді функцияның жоғарыда айтылғанмен тағы бір мәндес анықтамасын тұжырымдайық.
жиынының бір ғана элементі сәйкес келеді, не ешбір элементі сәйкес келмейді. Енді функцияның жоғарыда айтылғанмен тағы бір мәндес анықтамасын тұжырымдайық.
Функция деп кез келген
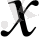 элементіне, бірінші элементі осы
элементіне, бірінші элементі осы
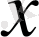 болатындай, біреуден артық емес
болатындай, біреуден артық емес
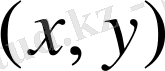 пары сәйкес келетін
пары сәйкес келетін
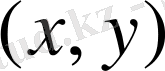 парларының
парларының
 жиынын айтады. Егер
жиынын айтады. Егер
 жиынын функция десек, онда
жиынын функция десек, онда
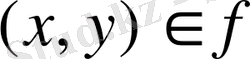 сөйлемін
сөйлемін
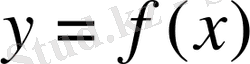 арқылы жазады да
арқылы жазады да
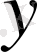 -ті
-ті
 функциясының аргумент
функциясының аргумент
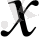 мәніне сәйкес мәні деп атайды. Немесе былай жазады:
мәніне сәйкес мәні деп атайды. Немесе былай жазады:
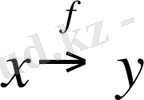 .
.
 функциясының анықталу облысы деп
функциясының анықталу облысы деп
 жиынына енетін парлардың барлық бірінші элементтерінің жиынын атайды да,
жиынына енетін парлардың барлық бірінші элементтерінің жиынын атайды да,
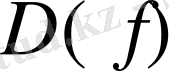 арқылы белгілейді.
арқылы белгілейді.
 функциясы мәндерінің облысы деп
функциясы мәндерінің облысы деп
 жиынынаенетін парлардың барлық екінші элементерінің жиынын атайды да
жиынынаенетін парлардың барлық екінші элементерінің жиынын атайды да
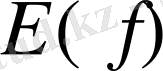 арқылы белгілейді.
арқылы белгілейді.
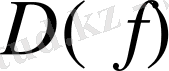 және
және
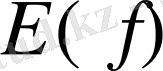 жиындары
жиындары
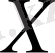 және
және
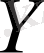 жиындарының сәйкес бөліктері дейік. Енді «бейнелеу» термині «функция» терминінің синонимі болатынын мына мысалдар арқылы көрсетуге болады.
жиындарының сәйкес бөліктері дейік. Енді «бейнелеу» термині «функция» терминінің синонимі болатынын мына мысалдар арқылы көрсетуге болады.
- Егерболса, ондадегеніміз-ті-ке бейнелеу болады.
- Егерболса, ондадегеніміз-ті-тің ішіне бейнелеу болады да, былай белгіленеді:, не.
- Егерболса, ондадегеніміз-тің белгілі бір бөлігін-ке бейнелеу болады.
- Егерболса, ондадегеніміз-тің белгілі бір бөлігін-тің ішіне бейнелеу болады.
Сонымен бірге,
 элементіне сәйкес келетін
элементіне сәйкес келетін
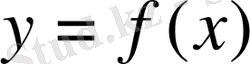 элементі
элементі
 бейнелеуінде
бейнелеуінде
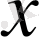 элементінің бейнесі деп аталады. Ал барлық
элементінің бейнесі деп аталады. Ал барлық
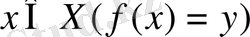 элементтерінің жиынын
элементтерінің жиынын
 элементінің толық алғашқы бейнесі деп атайды. Егер әрбір
элементінің толық алғашқы бейнесі деп атайды. Егер әрбір
 үшін
үшін
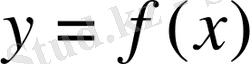 шартын қанағаттандыратын бір ғана
шартын қанағаттандыратын бір ғана
 элементі табылса, онда
элементі табылса, онда
 функциясы қайтымды функция деп аталады (
функциясы қайтымды функция деп аталады (
 бейнелеуі де қайтымды делінеді) . Қайтымды
бейнелеуі де қайтымды делінеді) . Қайтымды
 функциясының кері
функциясының кері
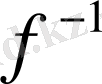 функциясы болады және былай жазылады:
функциясы болады және былай жазылады:
 .
.
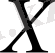 -тің
-тің
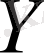 -ке қайтымды бейнеленуі
-ке қайтымды бейнеленуі
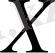 -тің
-тің
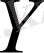 -ке өзара бір мәнді бейнеленуі деп аталады.
-ке өзара бір мәнді бейнеленуі деп аталады.
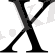 -тің
-тің
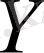 -ке өзара бір мәнді бейнеленуі
-ке өзара бір мәнді бейнеленуі
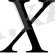 -ті түрлендіру деп аталады.
-ті түрлендіру деп аталады.
Сандық функция және оны анықтау.
Анықталу облысы мен мәндер облысы нақты сандар
 жиынының бөліктері болатын функциялар сандық функциялар деп аталады. Енді осы сандық функцияның анықтамасын келтірейік. Сандық функция деп, кез келген
жиынының бөліктері болатын функциялар сандық функциялар деп аталады. Енді осы сандық функцияның анықтамасын келтірейік. Сандық функция деп, кез келген
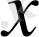 санына, бірінші элементі осы
санына, бірінші элементі осы
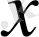 болатындай, біреуден артық емес
болатындай, біреуден артық емес
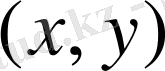 пары сәйкес келетін
пары сәйкес келетін
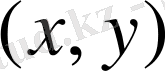 сандар парларының
сандар парларының
 жиынын айтады. Осы аталған бір ғана пардағы екінші санды
жиынын айтады. Осы аталған бір ғана пардағы екінші санды
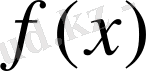 арқылы белгілейді:
арқылы белгілейді:
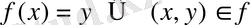 , немесе
, немесе
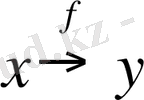 .
.
 функциясы
функциясы
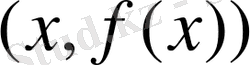 парлары жиынының берілуімен толық анықталады, мұндағы
парлары жиынының берілуімен толық анықталады, мұндағы
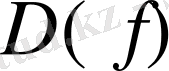 жиынының барлық мәнін
жиынының барлық мәнін
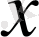 қабылдайды да, ал
қабылдайды да, ал
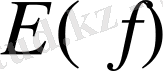 жиынының барлық мәнін
жиынының барлық мәнін
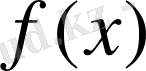 қабылдайды.
қабылдайды.
Мысалдар.
1.
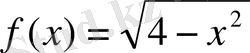 формуласы
формуласы
 функциясын анықтайды, оның анықталу облысы
функциясын анықтайды, оның анықталу облысы
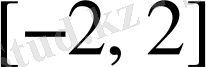 кесіндісі де, ал мәндер облысы
кесіндісі де, ал мәндер облысы
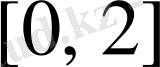 кесіндісі болады.
кесіндісі болады.
2.
 бейнелеуі функция болады, оның анықталу облысы
бейнелеуі функция болады, оның анықталу облысы
 жиыны да, ал мәндер облысы - теріс емес нақты сандар жиыны.
жиыны да, ал мәндер облысы - теріс емес нақты сандар жиыны.
Функцияның берілу тәсілдері
- Функцияның парларды атау (кесте) арқылы берілуі
Бірінші элементтері анықталу облысын, ал екінші элементтері мәндер облысын құрайтын парлар жиынымен функцияның толық анықталатынын біз бұрыннан білеміз. Егер функцияның анықталу облысы ақырлы жиын болса, мұндай функцияны барлық парларды атап көрсету арқылы беруге болады, яғни сол парлар жиынын мына кесте түрінде жазамыз:
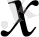
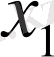
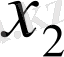
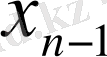
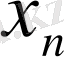
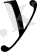

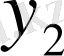
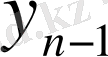
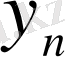
Сонда
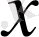 айнымалысының мәндері
айнымалысының мәндері
 функциясының анықталу облысын құрайды да, ал
функциясының анықталу облысын құрайды да, ал
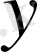 мәндері функция мәндері облысын құрайды. Сандық функция үшін
мәндері функция мәндері облысын құрайды. Сандық функция үшін
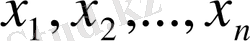 және
және
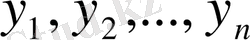 нақты сандар болады. Жалпы алғанда, кесте функцияны толық сипаттайды деуге болмайды.
нақты сандар болады. Жалпы алғанда, кесте функцияны толық сипаттайды деуге болмайды.
Шынында да, функция толық берілу үшін оның кейбір мәндерін ғана емес, барлық парлар жиынын білу керек болады. Алайда іс жүзінде функция мәндерінің кестесін тәжірибеге сүйеніп қана құрып жүрміз. Өзіміз білетін сандар квадарттарының, кубтарының, түбірлерінің, логарифмдерінің кестелері, сондай-ақ, тригонометриялық функциялар т. б. мәндер таблицаларының (кесетелерінің) әрқайсысы функциялар мәндерінің кестесі болып табылады.
- Функцияның анлитикалық тәсілмен берілуі.
Математикалық анализде формула түрінде жазылған екі айнымалы өрнекпен сандық функцияның берілуі аса жиі кездеседі. Бұны функцияның аналитикалық тәсілмен берілуі деп атайды. Бұлайша берілу тәсілі анықталу облысы ақырсыз жиын болып келген функцияларды сипаттап көрсетуге аса қолайлы.
Мысалы,
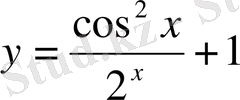 формуласы қандай болса да бір
формуласы қандай болса да бір
 функциясын анықтайды. Кейде бір ғана аналитикалық өрнектің өзі анықталу облысына байланысты әр түрлі функцияларды анықтауы мүмкін екенін айта кеткен жөн.
функциясын анықтайды. Кейде бір ғана аналитикалық өрнектің өзі анықталу облысына байланысты әр түрлі функцияларды анықтауы мүмкін екенін айта кеткен жөн.
Егер
 функциясы
функциясы
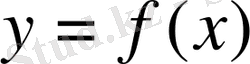 формуласымен беріліп, бірақ анықталу облысы көрсетілмесе, онда оның анықталу облысы аналитикалық
формуласымен беріліп, бірақ анықталу облысы көрсетілмесе, онда оның анықталу облысы аналитикалық
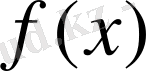 өрнегінің анықталу облысымен дәл келеді деп түсініледі. Мысалы,
өрнегінің анықталу облысымен дәл келеді деп түсініледі. Мысалы,
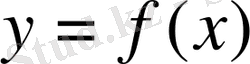 функциясы
функциясы
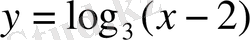 формуласымен берілсін (анықталу облысы көрсетілмеген дейік) . Сонда
формуласымен берілсін (анықталу облысы көрсетілмеген дейік) . Сонда
 шартын қанағаттандыратын
шартын қанағаттандыратын
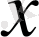 мәндері жиыны (
мәндері жиыны (
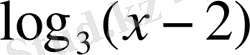 өрнегінің анықталу облысы), яғни
өрнегінің анықталу облысы), яғни
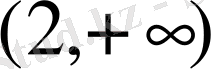 интервалы бұл функцияның анықталу облысы болып табылады.
интервалы бұл функцияның анықталу облысы болып табылады.
3. Функцияның график арқылы берілуі
Сандық жиындар арасындағы қатынасты (тәуелділікті) көрнекі түрде, оның графигін пайдалана отырып көрсетуге болады. Ол үшін жазықтықта барлық
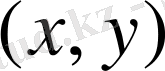 нүктелерін салу жеткілікті; сонда
нүктелерін салу жеткілікті; сонда
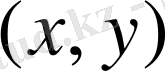 парларының бірінші элементтері абсциссалар да, ал екіншілері - ординатарлар. Егер де график бойында абсциссалары бірдей нүктелер болмаса, яғни әрбір абсциссаға тек бір ғана ордината сәйкес келетін болса, онда осы графикпен анықталатын қатынас функция болады.
парларының бірінші элементтері абсциссалар да, ал екіншілері - ординатарлар. Егер де график бойында абсциссалары бірдей нүктелер болмаса, яғни әрбір абсциссаға тек бір ғана ордината сәйкес келетін болса, онда осы графикпен анықталатын қатынас функция болады.
Мысал.
Шеңбер мен жарты шеңбер қатынастарының графиктері болады (2а, б-суреттер) олардың анықталу облысы
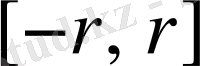 . Алайда шеңбер (2а-сурет) функция графигі болмайды, ал жарты шеңбер (2б-сурет) функция графигі болады. 2в-суретте көрсетілген графикте функция графигі бола алмайды. Функцияның график арқылы берілуі іс жүзінде өзі сызатын алуан түрлі приборлар көмегімен жүзеге асырылады.
. Алайда шеңбер (2а-сурет) функция графигі болмайды, ал жарты шеңбер (2б-сурет) функция графигі болады. 2в-суретте көрсетілген графикте функция графигі бола алмайды. Функцияның график арқылы берілуі іс жүзінде өзі сызатын алуан түрлі приборлар көмегімен жүзеге асырылады.
Сандық функциялардың кластарға бөлінуі мен қарапайым сипаттамалары
- Сандық функциялардың кластарға бөлінуі
Сандық функцияларды аналитикалық өрнектері мен қасиеттеріне қарай екі класқа бөлуге болады. Бұл жолы біз аналитикалық өрнектеріне қарай функциялардың қалай бөлінетінін қарастырамыз.
 функциясы
функциясы
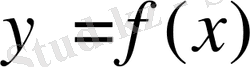 формуласымен берілсін. Енді
формуласымен берілсін. Енді
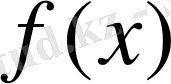 өрнегі үшін әр түрлі жағдайларды қарастырайық.
өрнегі үшін әр түрлі жағдайларды қарастырайық.
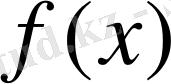 өрнегін алу үшін
өрнегін алу үшін
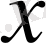 аргументі мен тұрақты сандарға саны шектеулі алгебралық амалдар (қосу, алу, көбейту, бөлу, түбір табу) қолданылатын болса, онда өрнекті алгебралық өрнек деп атайды. Алгебралық өрнектердің анықталу облысы мына шарттармен шектеледі: тек теріс емес сандардан ғана жұп көрсеткішті түбір табуға болады, нөлге бөлуге болмайды. Әрбір алгебралық
аргументі мен тұрақты сандарға саны шектеулі алгебралық амалдар (қосу, алу, көбейту, бөлу, түбір табу) қолданылатын болса, онда өрнекті алгебралық өрнек деп атайды. Алгебралық өрнектердің анықталу облысы мына шарттармен шектеледі: тек теріс емес сандардан ғана жұп көрсеткішті түбір табуға болады, нөлге бөлуге болмайды. Әрбір алгебралық
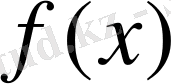 өрнегі алгебралық делінетін
өрнегі алгебралық делінетін
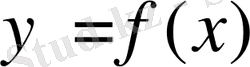 формуласымен берілген
формуласымен берілген
 функциясымен байланысты. Алгебралық өрнектің анықталу облысы бос жиын болуы мүмкін. Әрине ондай өрнек бос функцияны анықтайды. Алайда біз бос функцияны қарастырмаймыз.
функциясымен байланысты. Алгебралық өрнектің анықталу облысы бос жиын болуы мүмкін. Әрине ондай өрнек бос функцияны анықтайды. Алайда біз бос функцияны қарастырмаймыз.
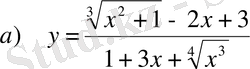 формуласымен берілген функция алгебралық функция болады.
формуласымен берілген функция алгебралық функция болады.
б)
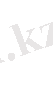 Алгебралық
Алгебралық
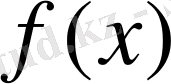 өрнегін құру үшін түбір табу амалы қолданылмаса, оны рационал өрнек деп атайды да, оған сәйкес функцияны рационал функция дейді.
өрнегін құру үшін түбір табу амалы қолданылмаса, оны рационал өрнек деп атайды да, оған сәйкес функцияны рационал функция дейді.
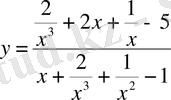 формуласымен анықталған функция рационал функция болады.
формуласымен анықталған функция рационал функция болады.
в) Рационал
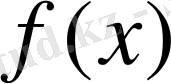 өрнегін құру үшін бөлу амалы қолданылмаса, оны бүтін рационал бөлшек деп атайды да, оған сәйкес функцияны бүтін рационал функция дейді. Бүтін рационал өрнекті көпмүше деп те атайды. Мұндай функциялардың мысалы ретінде сызықтық
өрнегін құру үшін бөлу амалы қолданылмаса, оны бүтін рационал бөлшек деп атайды да, оған сәйкес функцияны бүтін рационал функция дейді. Бүтін рационал өрнекті көпмүше деп те атайды. Мұндай функциялардың мысалы ретінде сызықтық
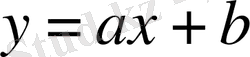 , квадраттық
, квадраттық
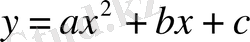 т. б. функцияларды қарастыруға болады. Кез-келген рационал
т. б. функцияларды қарастыруға болады. Кез-келген рационал
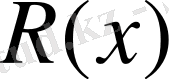 өрнегін стандарт түрде былай жазуға болады:
өрнегін стандарт түрде былай жазуға болады:

(мұндағы
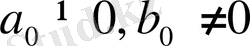 ) яғни екі бүтін рационал өрнектің қатынасы ретінде жазылады.
) яғни екі бүтін рационал өрнектің қатынасы ретінде жазылады.
Алгебралық емес функцияларды трансценденттік функция деп атайды. Математиканың мектеп курсынан белгілі көрсеткіштік, логарифмдік,
тригонометриялық, кері тригонометриялық функциялардың барлығы да трансценденттік функциялар қатарына жатады. Сондай-ақ
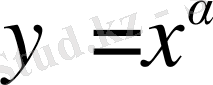 формуласымен (мұндағы
формуласымен (мұндағы
 -иррационал сан) анықталатын функция да трансценденттік функция болады.
-иррационал сан) анықталатын функция да трансценденттік функция болады.
2. Сандық функциялардың қарапайым сипаттамалары.
Сандық функциялардың өздеріне тән қасиеттеріне қарай сипаттамаларын қарастырайық.
а) Шенелген және шенелмеген функциялар
Егер
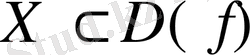 жиынында анықталған
жиынында анықталған
 функциясының сәйкес мәндерінің
функциясының сәйкес мәндерінің
 жиыны шенелген болса, онда ол функция
жиыны шенелген болса, онда ол функция
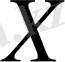 жиынында шенелген деп аталады.
жиынында шенелген деп аталады.
Жеке жағдайда,
 облысында шенелген
облысында шенелген
 функциясы үшін оның мәндер облысы
функциясы үшін оның мәндер облысы
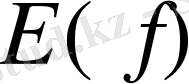 шенелген жиын болады. Енді шенелген жиынның бұрын айтылған анықтамасын пайдаланып шенелген функция үшін алдыңғымен пара-пар бір анықтаманы келтірейік: егер оң
шенелген жиын болады. Енді шенелген жиынның бұрын айтылған анықтамасын пайдаланып шенелген функция үшін алдыңғымен пара-пар бір анықтаманы келтірейік: егер оң
 саны табылып, барлық
саны табылып, барлық
 мәндері үшін
мәндері үшін
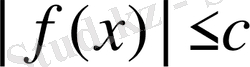 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
 функциясы
функциясы
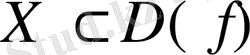 жиынында шенелген функция деп аталады (символдар арқылы:
жиынында шенелген функция деп аталады (символдар арқылы:
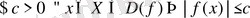 . )
. )
Осыған ұқсас түрде
 функциясының
функциясының
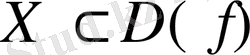 жиынында жоғарыдан (төменннен) шенелгендігінің анықтамасын келтіруге болады.
жиынында жоғарыдан (төменннен) шенелгендігінің анықтамасын келтіруге болады.
 және
және
 символдары көмегімен функцияның шенелмегендігінің анықтамасын келтіру үшін шенелмеген функция анықтамасындағы
символдары көмегімен функцияның шенелмегендігінің анықтамасын келтіру үшін шенелмеген функция анықтамасындағы
 символын
символын
 символымен, ал
символымен, ал
 символын
символын
 символымен алмастыру жеткілікті (қысқаша айтқанда, шенелмеген функция жөніндегі пікірді терістеу керек) . Сонымен, егер
символымен алмастыру жеткілікті (қысқаша айтқанда, шенелмеген функция жөніндегі пікірді терістеу керек) . Сонымен, егер
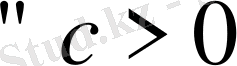 үшін
үшін
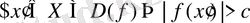 орындалса, онда
орындалса, онда
 функциясы
функциясы
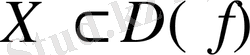 жиынында шенелмеген функция деп аталады.
жиынында шенелмеген функция деп аталады.
Мысалдар
1)
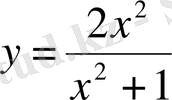 функциясы бүкіл сандық өсте шенелген. Шынында да,
функциясы бүкіл сандық өсте шенелген. Шынында да,
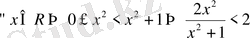 .
.
2)
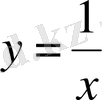 функциясы
функциясы
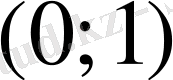 аралығында шенелмеген. Шынында да,
аралығында шенелмеген. Шынында да,
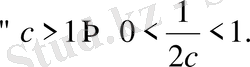 Бұдан
Бұдан
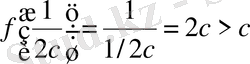 . Сонымен,
. Сонымен,
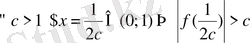 . Алайда кез келген
. Алайда кез келген
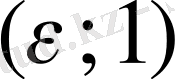 (мұндағы
(мұндағы
 ) аралығында бұл функция шенелген.
) аралығында бұл функция шенелген.
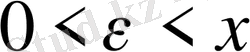 үшін
үшін
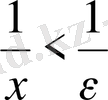 теңсіздігі орындалады. Енді
теңсіздігі орындалады. Енді
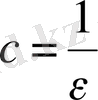 десек, онда
десек, онда
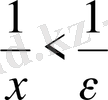 теңсіздігінен барлық
теңсіздігінен барлық
 үшін
үшін
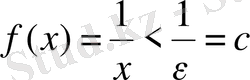 теңсіздігі орындалады. Сонымен,
теңсіздігі орындалады. Сонымен,
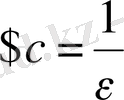
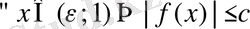 .
.
б) Жұп және тақ функциялар
Егер
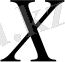 жиынына әрбір
жиынына әрбір
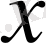 санымен бірге оған қарама-қарсы
санымен бірге оған қарама-қарсы
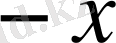 саны да енетін болса, онда
саны да енетін болса, онда
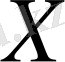 жиыны координаталар бас нүктесіне қатысты симметриялы жиын деп аталады. Анықталу облысы координаталар бас нүктесіне қатысты симметриялы
жиыны координаталар бас нүктесіне қатысты симметриялы жиын деп аталады. Анықталу облысы координаталар бас нүктесіне қатысты симметриялы
 жиыны болатын
жиыны болатын
 функциясы үшін, егер кез келген
функциясы үшін, егер кез келген
 мәніне сәйкес
мәніне сәйкес
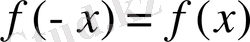 теңдігі орындалса, онда оны
жұп функция
деп атайды (символдар арқылы
теңдігі орындалса, онда оны
жұп функция
деп атайды (символдар арқылы
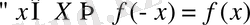 ) .
) .
Анықталу облысы координаталар бас нүктесіне қатысты симметриялы
 жиыны болып табылатын
жиыны болып табылатын
 функциясы үшін, егер
функциясы үшін, егер
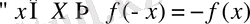 болса, онда оны
тақ функция
деп атайды. Егер де функцияның анықталу облысы
болса, онда оны
тақ функция
деп атайды. Егер де функцияның анықталу облысы
 координаталар бас нүктесіне қатысты симметриялы жиын болмаса, онда функция жұп та, тақ та болмайды.
координаталар бас нүктесіне қатысты симметриялы жиын болмаса, онда функция жұп та, тақ та болмайды.
- Бір айнымалы функцияларды зерттеу
Берілген функцияны схемалық түрде зерттеу
Анықтама:
Егер екі айнымалы шама (х; у) бір-бірімен функциялық тәуелдікте болып, біреуінің (х) әрбір мүмкін мәніне екіншісінің (у) белгілі бір мәні сәйкес келетін болса, онда у айнымалысы х-тің функциясы деп аталады. Ал х аргумент делінеді. Функциялық байланыстылық былайша жазылады: у=f(x), мұны « Игрек икстен эфке тең» деп оқиды. Ал функцияның графигі деп абциссалары аргумент, ал ординаталары функцияның сәйкес мәндері болатын нүктелердің геометриялық орнын айтамыз. Яғни берілген функцияның Х жиынындағы М(х; f(x) ) мұндағы, х
 Х түріндегі координаттық жазықтықтағы нүктелерден құралған Г қисығын осы функцияның графигі деп атаймыз. Функция көбінесе графиктермен беріледі. Алғашында функциялардың графиктерін «нүктелері бойынша» салып жүрдік, бірақ ол кейбір жағдайда дәл, нақты нәтиже бермейді. Графикті қателеспей салу үшін, функцияның өзіне тән ерекшеліктерін айқындай білуге үйрену, яғни оны алдын ала зерттеп бірнеше пункттен тұрады.
Х түріндегі координаттық жазықтықтағы нүктелерден құралған Г қисығын осы функцияның графигі деп атаймыз. Функция көбінесе графиктермен беріледі. Алғашында функциялардың графиктерін «нүктелері бойынша» салып жүрдік, бірақ ол кейбір жағдайда дәл, нақты нәтиже бермейді. Графикті қателеспей салу үшін, функцияның өзіне тән ерекшеліктерін айқындай білуге үйрену, яғни оны алдын ала зерттеп бірнеше пункттен тұрады.
Функцияның зерттеу схемасы немесе жоспары.
- Функцияның анықталу облысын табу;
- Функцияны жұп, тақтыққа зерттеу;
- Функцияның абцисса осімен қиылысу нүктесін табу;
- Функцияның үзіліс нүктесін табу;
- 3 және 4 пунктте табылған нүктелер арқылы абцисса осін бірнеше аралықтарға бөліп, әрбір аралықтағы функцияның таңбасын анықтау;
- Функцияның үзіліс нүктесі аймағы мен шексіздіктегі қасиеттерін қарастырып, оның асимптоталарын табу;
- Асимптотаға сәйкес функция графигінің орналасуы;
- Функцияның өсу, кему аралықтарын табу;
- Функцияның экстремум нүктелерін табу;
- Функцияны ойыс, дөңестікке зерттеп, иілу нүктесін табу;
- Функция графигінің эскизін салу.
Енді осы пункттерге жеке-жеке тоқталып әрқайсысына түсінік берейік:
Функцияның анықталу облысы
Функцияны зерттеген кезде аргументтің қандай мәндер қабылдайтынын білудің, яғни х-тің мәндерінің қандай болатындығын анықтаудың маңызы зор.
Анықтама
: y=f(x) функциясының х аргументінің, у функциясы анықталатын барлық мәндерінің жиыны осы функцияның анықталу облысы деп аталады. Функцияның анықталу облысына қосымша жағдайлар әсер етеді. Егер функция аналитикалық тәсілмен берілсе, онда функцияның анықталу облысы функцияны анықтайтын формула анықталатын аргументтің барлық мәндерінің жиынынан тұрады. Функция белгілі бір есептің шартынан құралса, мысалы: у- квадраттың ауданы, ал -х- қабырғасы болса, онда анықталу облысы х-тің оң мәндерінен тұрады. 1) y=x
2
; D(f) =(

2) y=x
2
; D(f) =[0; +
 ), x>0;
), x>0;
Функцияның жұп, тақтығы
А) Егер y=f(x) функциясы үшін оның анықталу облысындағы аргументтің таңбасын өзгерткеннен функцияның таңбасы өзгермесе, онда y=f(x) функциясы жұп функция деп аталады, яғни жұп функция үшін f(-x) =f(x) теңдігі орындалады.
Жұп функцияның графигі ординаталар осі бойынша симметриялы болады.
Б) Егер y=f(x) функциясы үшін оның анықталу облысындағы аргументтің таңбасын өзгерткенде функция тек таңбасын ғана өзгертетін болса, онда y=f(x) функциясын тақ функция деп атайды, яғни тақ функция үшін f(-x) =-f(x) теңдігі орындалады.
Тақ функцияның графигі координаталар басына қарағанда симметриялы болады. Кейбір функциялар жұп та, тақ та емес болуы мүмкін.
Функция графигінің абцисса осімен қиылысу нүктесі
Функцияның абцисса осімен қиылысу нүктесін табу үшін f функциясын 0-ге теңестіреміз, яғни f(x) =0 теңдеуін шешеміз. Осы теңдеуден табылған түбір функцияның абцисса осімен қиылысу нүктесі болып табылады. Ізделінді нүктеміз осы.
Функцияның үзіліссіздігі
y=f(x) функциясының берілген анықталу облысында х аргументтің кез келген мәніне у функциясының сан мәні сәйкес келетін болса, у функциясы үзіліссіз болады. Яғни, а
 Д(f)
Д(f)
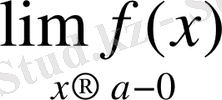 =
=
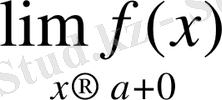 =
=
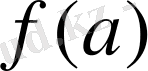 түрінде жазуға болады.
түрінде жазуға болады.
f(a-0) =f(a+0) =f(a) а
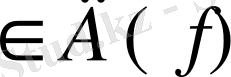 болса f(x) функциясы а нүктесінде үзіліссіз болады.
болса f(x) функциясы а нүктесінде үзіліссіз болады.
Функцияның таңбасы
5 пунктті жүзеге асыру үшін 3 және 4 пункттерді пайдалану керек деп шартта айтылған болатын, яғни фукцияның нольдері (немесе f(x) =0 теңдеуін шешкен кездегі түбірлері) оның абциссалар осімен қиылысу (жанасу) нүктелерінің абциссалары болады. Функцияның нөлдері мен таңба тұрақтылығы бір-бірімен байланысты болады. Функция өзінің таңбасын нөлдерінің маңында өзгертеді.
y=f(x) функциясының х 1 нүктесіне дейінгі таңбасы оң (графигі абцисса осінен жоғары), х 1 мен х 2 аралығында таңбасы теріс (графигі абцисса осінен төмен) х 2 мен х 3 , х 3 пен х 4 аралықтары оң, х 3 жанасу нүктесі болады. Функцияның анықталу облысындағы таңбасы өзгермейтін интервалы таңба тұрақтылығы интервалы деп аталады.
Функцияның асимптоталары
Егер y=f(x) функциясы берілсе, оның графигін салу процесінде х
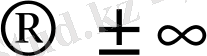 кездердегі функцияның өзгеруін болжаудың және аргументтің қандай мәндерінде у
кездердегі функцияның өзгеруін болжаудың және аргументтің қандай мәндерінде у
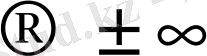 болатынын бағалаудың маңызы бар.
болатынын бағалаудың маңызы бар.
Егер функцияның графигінің тармағы шектеусіз ұзарғанда (х
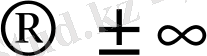 , у
, у
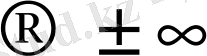 ) график түзуге шексіз жақындай беретін болса, онда ол түзу функция графигінің асимптотасы деп аталады.
) график түзуге шексіз жақындай беретін болса, онда ол түзу функция графигінің асимптотасы деп аталады.
Егер y=f(x) функциясының графигінің нүктесі мен түзудің ара қашықтығы нүкте шексіз қашықтағанда нольге ұмтылатын болса, онда түзу графиктің асимптотасы деп аталады. Асимптотаның үш түрі болады:
- x=b - вертикаль асимптота;
- y=a - горизонталь асимптота;
- y=kx+b - көлбеу асимптота;
Егер f(x) функциясы f(x) =kx+b+
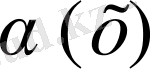 түрінде берілсе, онда y=kx+b түзуі х
түрінде берілсе, онда y=kx+b түзуі х
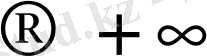 үшін f(x) функциясының көлбеу асимптотасы деп аталады, мұндағы
үшін f(x) функциясының көлбеу асимптотасы деп аталады, мұндағы
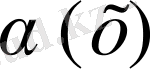 - ақырсыз аз функция. Егер k=0 онда y=b горизонталь асимптота. Мұндағы, k=
- ақырсыз аз функция. Егер k=0 онда y=b горизонталь асимптота. Мұндағы, k=
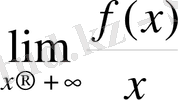 және b=
және b=
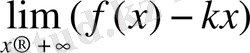
Функцияның өсу, кему аралықтары
Егер аргументтің қандай да бір интервалдан алынған кез келген мәнінің үлкеніне функцияның үлкен мәні сәйкес болса, онда функция сол интервалда өспелі функция деп аталады. Егер [a; b] сигментіндегі х 1 >x 2 мәндері үшін f(x 1 ) >f(x 2 ) болса, онда y=f(x) - өспелі функция болады.
Егер аргументтің қандай да бір интервалдан алынған екі мәнінің үлкеніне функцияның кіші мәні сәйкес болса, онда функция сол интервалда кемімелі деп аталады.
Егер [a; b] сегментіндегі х 1 >x 2 мәндері үшін f(x 1 ) <f(x 2 ) болса, онда функция кемімелі болады. Функция өзінің анықталу облысында кейбір бөлігінде өспелі, ал кейбіреуінде кемімелі болуы мүмкін.
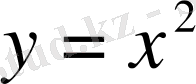 Equation. 3 ;
Equation. 3 ;
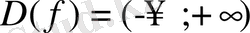
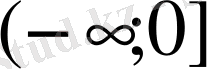
 , [0; +
, [0; +
 Equation. 3 )
Equation. 3 )
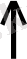 Equation. 3
Equation. 3
Алынған интервалда не өсетін, не кемитін функциялар монотонды функциялар деп аталады.
Сонымен қатар функцияның өсу, кему аралығын сол функцияның туындысын пайдаланып анықтауға болады. Егер берілген интервалда функция туындысы0-ден кіші, яғни,
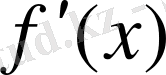 <0 болса, осы интервалда кемімелі, ал егер
<0 болса, осы интервалда кемімелі, ал егер
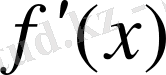 >болса, осы интервалда функция өспелі болады.
>болса, осы интервалда функция өспелі болады.
Функцияның экстремум нүктелері
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz