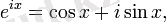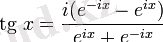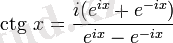Комплекс сандар: анықтамасы, тригонометриялық және көрсеткіштік формалары, амалдар және n-ші дәрежелі түбірлер


Жоспары:
Кіріспе . . . 3
1. Комплекс сандар ұғымы . . . 4
2. Комплекс санының тригонометриялық мағынасы және көрсеткіштік формалары . . . 7
2. 1 Комплекс сандарға амалдар қолдану . . . 8
Қорытынды . . . 11
Пайдаланылған әдебиеттер тізімі
Кіріспе
Алгебраның дамуына байланысты бұрыннан белгілі он және теріс сандармен қатар жаңа сандар енгізу қажеттілігі туындалады. Осыған байланысты «Жорамал бірлік», «Жорамал сан» ұғымдары қалыптасты, бірақ қазір комплекс сандар тек қана математикада, аэродинамикада, физикада кеңінен қолданылады.
Комплекс сан дегеніміз- екі реттелген нақты сандардың қосындысын айтамыз.
Комплекс санының алгебралық формуласы:
Мұндағы нақты сандар, - жорамал бірліктің квадраты, яғни
жорамал бөлігі.
Егер болады, яғни нақты сан шығады.
және түйіндес комплекс сандар.
1. Комплекс сандар ұғымы
Комплекс сандар алгебралық теңдеулерді шешу негізінде пайда болды.
Комплекс сан деп z=a+bi түріндегі санды айтамыз, мұндағы a және b -нақты сандар, ал i -жорамал бірлік, i 2 =-1. a комплекс санның нақты бөлігі, b -оның жорамал бөлігі. Re(z) = a, Im(z) = b
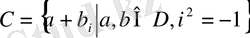 - комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі,
- комплекс сандар жиыны. Әрбір нақты сандар комплекс сан деп қабылдауға болады, себебі,
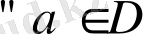 үшін
үшін
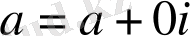 .
.
Комплекс сандар жиыны нақты сандар жиынының кеңеюі
 .
.
z=
a+bi
және
 =
a-bi
өзара
түйіндес сандар
деп аталады
=
a-bi
өзара
түйіндес сандар
деп аталады
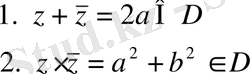
z
1
=
a+bi
және z
2
=
c+di
cандары тең

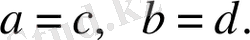
Комплекс сандарының қосындысы комплекс сан болады.
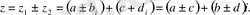
Қосудың қасиеттері:
∀z 1 , z 2 , z 3 ∈C үшін (z 1 +z 2 ) +z 3 =z 1 +(z 2 +z 3 ),
∃0∈C, ∀z∈C, z+0=0+z=z,
∀z∈C, ∃ -z∈C, z+(-z) =(-z) +z=0,
∀z 1 , z 2 ∈C; z 1 +z 2 =z 2 +z 1 .
Комплек сандардың көбейтіндісі комплекс сан.
z=z 1 ⋅z 2 =(a+bi) ⋅(c+di) =(ac-bd) +(bc+ad) i.
Көбейтудің қасиеттері:
∀z 1 , z 2 , z 3 ∈C (z 1 ⋅z 2 ) ⋅z 3 =z 1 ⋅(z 2 ⋅z 3 ) (ассоциативті),
∃1∈C, ∀z∈C, z⋅1=1⋅z=z (1=1+0⋅ i ),
∀z∈C, ∃ z -1 ∈C, z⋅z -1 =z -1 ⋅z=1 (z= a+bi және z -1 = 1/z=( a/(a 2 +b 2 ) ) +((- b ) /( a 2 +b 2 ) ) i ),
∀z 1 , z 2 ∈C, z 1 ⋅z 2 =z 2 ⋅z 1 (коммутативті) .
Қосу мен көбейту амалдары дистрибутивтілік заңымен байланысқан
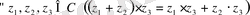 .
.
Комплекс сандардың бөліндісі комплекс сан,
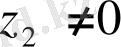
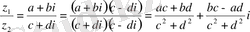
Комплекс сандардың геометриялық мағынасы және тригонометриялық түрі.
Комплекс сандарды координат жазықтығының көмегімен жазықтықтың нүктелері ретінде өрнектеуге болады. O
x -
осінің бойына комплекс санның нақты бөлігін
(a=a
+0∙
i),
ал O
y
осінің бойына оның жорамал бөлігін орналастырсақ (
bi=0+bi)
жазықтықта әрбір комплекс сан z(
a, b
) нүктесі түрінде анықталады.
 тік бұрышты
тік бұрышты
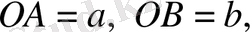 z
z
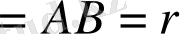 r
=z=
r
=z=
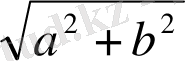 .
.
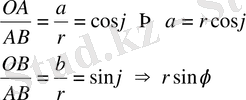
z= a+bi=r( cosφ+isinφ) - комплекс санның тригонометриялық түрі.
 =r - комплекс санның модулі
=r - комплекс санның модулі
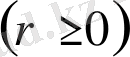 .
.
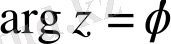 -комплекс санның аргументі.
-комплекс санның аргументі.
Тригонометриялық түрдегі комплекс сандарға амалдар қолдану өте жеңіл.
Айталық,
z 1 = r 1 (cosφ 1 +isinφ 1 ),
z 2 = r 2 (cosφ 2 +isinφ 2 ) болсын.
Онда
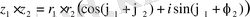
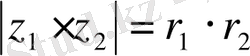
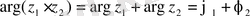
Егер
 болса, онда
болса, онда
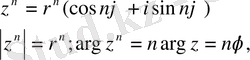
Муавр формуласы
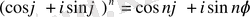
Комплекс саннан n ші дәрежелі түбір табу және 1 ден табылған түбірлердің группасы.
Айталық,
а=r(cos
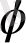 +isin
+isin
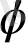 )
комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін
)
комплекс саны берілсін. Онда жоғарыда қарастырылған көбейту амалының негізінде n- натурал саны үшін
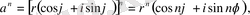
яғни комплекс санды дәрежелегенде оның модулі сол дәрежеге шығарылады, ал аргументі сол дәреже көрсеткішіне көбейтіледі.
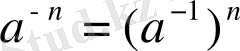
теңдігін пайдаланып, Муавр формуласын бүтін теріс сандар үшін де пайдалануға болады.
a=a+bi комплекс санын оң бүтін n дәрежеге шығару үшін Ньютонның биномын пайдаланған орынды, тек

ескерсек жеткілікті.
Муавр формуласының дербес түрін қарастырайық.
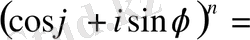 cos n
cos n
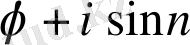
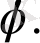
Теңдіктің оң жақ бөлігіне Ньютонның биномды формуласын қолданайық.
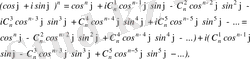
Мұндағы
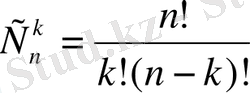
теңдігінің сол және оң жақ бөліктерін салыстырсақ,
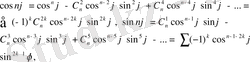
теңдіктерін аламыз.
Сонымен,
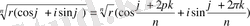 , мұндағы
, мұндағы
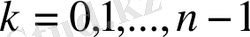
ға әртүрлі мәндер беру арқылы түбірдің әртүрлі мәндерін аламыз.
Қорытынды. Комплекс сандардан n - ші дәрежелі түбірді әрқашан табуға болады және оның әртүрлі n мәні болады.
z=a+bi
Y
X
O
a
b Ф
r
ϕ
2. Комплекс санының тригонометриялық мағынасы және көрсеткіштік формалары
Толық мақаласы: Эйлер формуласы
Эйлер формуласы кез келген нақты
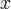 үшін келесі теңдік орындалады дейді:
үшін келесі теңдік орындалады дейді:
мұндағы
 - натурал логарифм негізі,
- натурал логарифм негізі,
- жалған бірлік.
Эйлер формуласымен
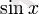 пен
пен
 функцияларын былай анықтауға болады:
функцияларын былай анықтауға болады:
,
.
Содан:
2. 1 Комплекс сандарға амалдар қолдану.
1. Егер екі комплекс сандардың нақты бөлігі мен нақты бөлігі, жорамал бөлігі мен жорамал бөлігі тең болса, онда бұл комплекс сандарды өзара тең деп атаймыз, яғни егер z=a+bi, w=c+di комплекс сандары үшін a=c, b=d теңдіктері орындалса, онда z және w комплекс сандарын өзара тең деп есептейміз және оны былай белгілейді: z=w .
2. z=a+bi және w=c+di комплекс сандардың қосындысы деп a+c+(b+d) i комплекс санын айтады, яғни z+w=a+ib+c+id=a+c+ib+d. Сонымен, екі комплекс сандарды қосу үшін олардың нақты бөлігі мен нақты бөлігін, жорамал бқлігі мен жорамал бөлігін қосса, жеткілікті.
Комплекс сандарды азайту z-w=a+ib-c+id=a-c+i(b-d)
- z=a+biжәнеw=c+diкомплекс
ac-bd+i(ad+bc) түріндегі комплекс санды айтады, яғни z∙w=a+ib∙c+id=ac-bd+i(ad+bc) . Осыдан екі комплекс санды көбейтуді көпмүшені көпмүшеге көбейту ережесімен орындап, i2=-1 теңдігін ескерсе, жеткілікті болады.
z=a+ib және z=a-ib түріндегі комплекс сандарын өзара түйіндес комплекс сандар деп аталады. Түйіндес комплекс сандардың көбейтіндісі нақты сан болады.
Егер екі комплекс санның нақты бөліктерінің де, жорамал бөліктерінің де таңбалары қарама-қарсы болса, онда оларды қарама-қарсы комплекс сандар деп атайды. Қарама-қарсы комплекс сандардың қосындысы 0-ге тең.
z=a+ib комплекс саны үшін a2+b2 теріс емес санын оның модулі деп атайды және модульді z арқылы белгілейді, яғни z =a2+b2 . Осыдан әрбір z комплекс саны мен оның түйіндесі z үшін z∙z=z2 теңдігі орындалатынын көреміз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz