Сызықтық программалау есептері және оларды шешу әдістері

КІРІСПЕ
«Амалдарды зерттеу» - әртүрлі жүйелерді тиімді басқарудың тәсілдерін зерттеп, оны практикада қолдануға және әртүрлі өндірістік есептердің ғылыми негізделінген бір ғана дұрыс шешімін табуға мүмкіндік беретін, ғылыми пәндердің бірі. Амалдарды зерттеудегі арнайы тәсілдерге : сызықтық программалау, оптимизация әдістері, дөңес программалау модельдері, динамикалық программалау, жаппай қызмет көрсету теориясы, ойындар теориясы, графтар теориясы жатады.
Амалдарды зерттеу қолданбалы математиканың бір тармағы ретінде өткен ғасырдың 40-50 жылдарында қалыптасты. Кейінгі елу жыл шамасында алынған фундаментальды теориялық нәтижелерді әртүрлі практикалық есептерді шешіге пайдаланылып келеді. Нәтижесінде амалдарды зерттеу экономикалық білімге қажетті классикалық ғылыми пән ретінде жетілдірілді.
Амалдарды зерттеудің міндеттері мен шешілуі жетілмеген мәселелері туралы айтқанда , оларды шешу жолында өзінің айтарлықтай үлесін қосқан, 1975 жылғы Нобель сыйлығының лауреты, академик Л. В. Канторовичтің экономикада ресурстарды тиімді қолдану жөніндегі еңбектерін ерекше атауға болады.
Математикалық әдістерді экономикалық зерттеулерде тәжірибе жүзінде қолдану 1951жылы басталды, ал 1955 жылдары кеңінен қолданылатын болды. Математиканың экономикаға енуі жоспарлау мен басқарудың қазіргі кездегі ғылыми-техникалық революциясының аса маңызды ерекшелігі болып табылады.
Бұл процесс соңғы 50 жыл көлемінде бүкіл әлемде қарқынды түрде жүргізілуде. Математикалық әдіс мектептерінің АҚШ, Франция, ГФР, Англияда ашылуының объективті себептері мол.
Жоспарлы тапсырма қабылдауда экономикалық-математикалық әдістердің мәні ерекше. Экономикалық-математикалық әдістер–экономика және математика пәндерінің комплексі. «Экономикалық-математикалық әдістері» терминін ХХ ғ.60-жылдардың басында академик В.С.Немчинов енгізген.
Кез келген математикалық модель нақты дүниенің қандай да бір класының математикалық символдар түрінде бейнеленуін көрсетеді.
Амалдарды зерттеу бұл математикалық пәндердің кешені .
Амалдар деп ортақ бір ниетпен бірлескен, нақты бір мақсатқа жетуге бағытталған, кез келген іс-шараны (немесе әрекеттер жүйесі) айтамыз.
Амалдарды зеттеу әдістері қандай да бір амалды(операцияны ) іске асыру үшін қолданылатын әрекеттер жиынтығы.
Мысалы: қандай да бір бұйымды шығаруды жоспарлау, сұраныс жасап отырған елді мекенге жүк, қажетті нәрлі заттар бар тамақ рационын таңдау т.с.с.
Операция екі түрлі мөлшер факторымен сипатталады: ағындағы жағдайда мәліметтері белгілі, бірақ шешім қабылдаушыға тәуелсіз болатын бақыланбайтын фактор және ағындағы жағдайда мәліметтері белгілі, шешім қабылдаушыға нақты бір шектеуде тәуелді болатын ,математикалық шектеулермен: теңсіздіктер, теңдіктер немесе арнайы шарттар арқылы өрнектелінген бақыланатын (басқарылатын) фактор.
Кез келген мүмкін болатын шешім мәндер жиыны ( яғни, берілген шектеулерді қанағаттандыратын) есептің шешуі болып табылады.
Табылған мүмкін болатын шешімдер саны көп болған жағдайда, олардың арасынан ең тиімдісін (оптималын) таңдау керек болады. Ол үшін сапа критерийі (оптимальды критерий) болуы шарт, ол функциясы арқылы өрнектелініп мақсатты функция деп аталынады. Оптималь шешім – бұл мақсатты функцияның экстремумы (максимум немесе миннимум мәні) болып есептеледі.

4.ӘДЕБИЕТТЕР
Негізгі:
1. Балапанов Е.Қ., Бөрібаев Б., Мадиярова Г. «Жаңа ақпараттық технологиялар» Алматы, 2000
2. Н.В.Апатова Инновационные технологии в школьном образовании.
- Москва : 1999
3. В.П.Беспалько Программированное обучение.Дидактические основы.
–Москва.: 1970
4. Под редакцией Е.С.Полат. Новые педагогоческие и информационные
технологии в ситеме образования. – М.: Academa,2003 г.

5.Малик Г.С. Основы экономики и математические методы в планировании Москва.:Высшая школа,1988.
6.Үсіпбаева М.Е. Кәсіпорынды басқару мен жоспарлаудың экономикалық – математикалық әдістері- А.: Рес.баспа кабинеті ,1996
Қосымша:
1.Нусупбеков С.И.,Устенова О.Ж. Экономикалық жүйені модельдеудің математикалық әдістері – Астана.:фолиант,2003
2.Акулич И.Л. Математическое программирование в примерах и задачах– М.:Наука 1998
3.В.П.Дьяконов Компьютерная математика.Теория и практика М.: НОЛИДЖ,2001
4.Куралбаев З.К. Решение задач по математическому программированию- Алматы :2001

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

МАЗМҰНЫ
КІРІСПЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
1. СЫЗЫҚТЫҚ ПРОГРАММАЛАУ ЕСЕПТЕРІ ЖӘНЕ ОЛАРДЫ
ШЕШУ ӘДІСТЕРІ
1.1 Сызықтық программалау туралы түсінік . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
1.1.1 Ресурстарды пайдалану туралы есеп. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
1.1.2 Қоспа туралы есеп (Диета туралы есеп). . . . . . . . . . . . . . .
. . . . . . . . . . . . . .
1.2 Сызықтық программалаудың жалпы есептері. Негізгі анықтамалар. . . . . .
. .
1.3 Көлік есебінің математикалық қойылымы. . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
1.4 Көлік есебінің моделдері . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
2. MS EXCEL ОРТАДАҒЫ АСПАПТЫҚ ҚҰРАЛДЫ ПАЙДАЛАНЫП ТАСЫМАЛДАУ МӘСЕЛЕЛЕРІН
ТИІМДІЛЕУ

2.1. Көлік есебінің алғашқы таяныш жоспарын құру. . . . . . . . . . . . . .
. . . . . . . . . .
2.2. Көлік есебінің оптимал шешімі. Потенциалдар әдісі. . . . . . . . . . .
. . . . . . . . . .
2.3 Көлік есебін компьютерде модельдеу үлгілері. . . . . . . . . . . . . .
. . . . . . . . . . . .
3.ҚОРЫТЫНДЫ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . .

КІРІСПЕ
Амалдарды зерттеу - әртүрлі жүйелерді тиімді басқарудың тәсілдерін
зерттеп, оны практикада қолдануға және әртүрлі өндірістік есептердің
ғылыми негізделінген бір ғана дұрыс шешімін табуға мүмкіндік беретін,
ғылыми пәндердің бірі. Амалдарды зерттеудегі арнайы тәсілдерге : сызықтық
программалау, оптимизация әдістері, дөңес программалау модельдері,
динамикалық программалау, жаппай қызмет көрсету теориясы, ойындар теориясы,
графтар теориясы жатады.
Амалдарды зерттеу қолданбалы математиканың бір тармағы ретінде
өткен ғасырдың 40-50 жылдарында қалыптасты. Кейінгі елу жыл шамасында
алынған фундаментальды теориялық нәтижелерді әртүрлі практикалық есептерді
шешіге пайдаланылып келеді. Нәтижесінде амалдарды зерттеу экономикалық
білімге қажетті классикалық ғылыми пән ретінде жетілдірілді.
Амалдарды зерттеудің міндеттері мен шешілуі жетілмеген мәселелері
туралы айтқанда , оларды шешу жолында өзінің айтарлықтай үлесін қосқан,
1975 жылғы Нобель сыйлығының лауреты, академик Л. В. Канторовичтің
экономикада ресурстарды тиімді қолдану жөніндегі еңбектерін ерекше атауға
болады.
Математикалық әдістерді экономикалық зерттеулерде тәжірибе жүзінде
қолдану 1951жылы басталды, ал 1955 жылдары кеңінен қолданылатын болды.
Математиканың экономикаға енуі жоспарлау мен басқарудың қазіргі кездегі
ғылыми-техникалық революциясының аса маңызды ерекшелігі болып табылады.
Бұл процесс соңғы 50 жыл көлемінде бүкіл әлемде қарқынды түрде
жүргізілуде. Математикалық әдіс мектептерінің АҚШ, Франция, ГФР, Англияда
ашылуының объективті себептері мол.
Жоспарлы тапсырма қабылдауда экономикалық-математикалық әдістердің
мәні ерекше. Экономикалық-математикалық әдістер–экономика және математика
пәндерінің комплексі. Экономикалық-математикалық әдістері терминін ХХ
ғ.60-жылдардың басында академик В.С.Немчинов енгізген.
Кез келген математикалық модель нақты дүниенің қандай да бір
класының математикалық символдар түрінде бейнеленуін көрсетеді.
Амалдарды зерттеу бұл математикалық пәндердің кешені .
Амалдар деп ортақ бір ниетпен бірлескен, нақты бір мақсатқа жетуге
бағытталған, кез келген іс-шараны (немесе әрекеттер жүйесі) айтамыз.
Амалдарды зеттеу әдістері қандай да бір амалды(операцияны ) іске асыру
үшін қолданылатын әрекеттер жиынтығы.
Мысалы: қандай да бір бұйымды шығаруды жоспарлау, сұраныс жасап
отырған елді мекенге жүк, қажетті нәрлі заттар бар тамақ рационын таңдау
т.с.с.
Операция екі түрлі мөлшер факторымен сипатталады: ағындағы жағдайда
мәліметтері белгілі, бірақ шешім қабылдаушыға тәуелсіз болатын
бақыланбайтын фактор және ағындағы жағдайда мәліметтері белгілі, шешім
қабылдаушыға нақты бір шектеуде тәуелді болатын ,математикалық
шектеулермен: теңсіздіктер, теңдіктер немесе арнайы шарттар арқылы
өрнектелінген бақыланатын (басқарылатын) фактор.
Кез келген мүмкін болатын шешім мәндер жиыны ( яғни, берілген
шектеулерді қанағаттандыратын) есептің шешуі болып табылады.
Табылған мүмкін болатын шешімдер саны көп болған жағдайда, олардың арасынан
ең тиімдісін (оптималын) таңдау керек болады. Ол үшін сапа критерийі
(оптимальды критерий) болуы шарт, ол 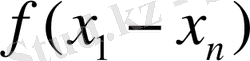функциясы арқылы өрнектелініп
мақсатты функция деп аталынады. Оптималь шешім – бұл мақсатты функцияның
экстремумы (максимум немесе миннимум мәні) болып есептеледі.

1. СЫЗЫҚТЫҚ ПРОГРАММАЛАУ ЕСЕПТЕРІ ЖӘНЕ ОЛАРДЫ
ШЕШУ ӘДІСТЕРІ
1.1 Сызықтық программалау туралы түсінік
Математикалық программалаудың бір бөлімі –сызықтық программалаудың мәні
болып табылады. Математикалық программалауға сызықтықпен қатар құрамдас
бөлігі ретінде бүтінсанды, параметрлік, сызықтық емес, квадраттық,
стохастикалық, динамикалық программалау енеді.
Сызықтық программалау есептерінің ерекшелігі сол, онда есептің мақсаты мен
шектеулері, сызықтық функция түрінде беріледі.
Берілген сызықтық шектеулерді қанағаттандыратын сызықтық функцияның
экстремумын (масимум және минимум) есептеп табу, сызықтық программалау
есептері болып табылады.
Сызықтық программалаудың дамуы экономикамен тығыз байланысты. Әрбір
кәсіпорын үшін өндірістің түрлі нұсқаын жоспарлауға болады. Сол жоспарға
сәйкес өндірілген өнім, одан алынған пайда әртүрлі болады. Кейбір
көрсеткіштердің шамасына сәйкес жоспардың бір нұсқаы жақсы, екіншісі–нашар
болуы мүмкін. Өндіріс жоспарының нақты көрсеткіштерге сәйкес барынша тиімді
болуы, ең көп пайда алуы, еңбек өнімділігінің жоғары болуы, т.с.с.
жоспардың оптималды екендігін көрсетеді, ал оны құру процесі оптималды
жоспарлау деп аталады.
Сызықтық программалаудың негізін 1930 жылы совет математигі
Л.В.Канторович қалады. Екінші дүниежүзілік соғыс жылдарында АҚШ қарулы
күштердің қызметін жоспарлау және қамтамассыз ету үшін сызықтық
программалау енгізілді. 1947жылы АҚШ-та сызықтық программалаудың ең негізгі
есептерінің бірі көлік есебінің моделін жасалынды.
Ал, 1947ж. американ ғалымы Дж. Данциг сызықтық программалау есептерін
шешетін симплекс әдісін ойлап тапты.
1949ж. Л.В.Канторович пен М.К.Гавурин көлік есебін шешетін тамаша
әдіс– потенциал әдісін ұсынды. Кейінгі жылдары көптеген елдердің ғалымдары
сызықтық программалаудың дамуына өз үлестерін қосты.
1.1.1 Ресурстарды пайдалану туралы есеп
Өндіріс орны , Р2 екі түрлі өнімді шығару үшін :, R2, R3 үш
түрлі ресурсты пайдаланады, олардың көлемі шектелген. Есептің бастапқы
мәндерін келесі кестеде көрсетеміз:
Кесте 2.1
Ресурстар Ресурстар Бір бірлік өнімді жасауға
түрі қоры жұмсалынған ресурс көлемі

36 6 6
20 4 2
40 4 8
Бір бірлік өнімді 12 15
сатудан түскен табыс,
тг.

Өнімді өткізгенде ең көп табыс әкелетін жоспар құру қажет.
Модельді құруды белгісіздерді белгілеуден бастаймыз. — арқылы
өнімнің көлемін, ал х2 — арқылы Р2, өнімнің көлемін белгілейміз.
Зерттеу объектісі – ретінде шектелген ресурстарды қолдана отырып, өнімді
шығару жоспарын құру керек. Ресурстар ретінде құрал -жабдықтар,
электроэнергиясы, жанармай, әртүрлі шикізат, жұмыс күші т.бс. Единицы
измерения количества продукции и ресурсов зависят от конкретного вида
продукции и ресурсов, рассматриваемых в задаче (например, для готовой
продукции, сырья, топлива — шт., кг, м, т, л и т. п.; для электроэнергии —
кВтч и т. д.).
Зерттеу мақсаты — өнімді шығарудан ең көп табыс әкелетін жоспар құру.
Есептің критерийі — максималды табыс. Бұл критерийді формальда түрде
былай жазамыз: өнімнің бір бірлігін өткізгеннен түскен табыс 12 тг.,
өнім көлемі —. Олай болса, барлық өнімді өткізгеннен түскен
табыс көлемі - 12 тг болады. Ал Р2 өнімнің бір бірлігін өткізгеннен
түскен табыс 15 тг., өнім көлемі — х2. Олай болса, барлық Р2 өнімді
өткізгеннен түскен табыс көлемі - 15x2 тг болады.. Р и Р2 өнімдерін
өткізгеннен түскен табыс максимальды болады деп , есептің критерийін былай
жазамыз:

Өндіріс орнындағы ресурстар көлемі шектелгендігін ескере отырып, оның да
математикалық моделін құрамыз.
Өндіріс орны үш түрлі ресурсты пайдалана отырып екі түрлі өнім шығарады.
Жұмсалынған ресурс көлемі өндірістегі бар ресурстар қорынан аспау керек. Әр
ресурстың өнімнің бір бірлігіне жұмсалынған көлемі және ресурстар қоры
белгілі болғандықтан, бұл жағдайды төмендегі шектеулер арқылы жазамыз::

Бірінші шектеудің мағынасы ресурсының және Р2 өнімдерін
шығаруға нақты жұмсалынған көлемі өндіріс орнындағы осы ресурстың қорынан
аспауы керек екендігін білдіреді. Екінші және үшінші шектеулердің R2, R3
ресурстар үшін мағынасы да осындай.
Шығарылған өнім көлемі 0 (егер өндіріс орны ешқандай өнім түрін
шығармаса) немесе оң шама болғандықтан, модельдегі оң айнымалылардың
шектеулері төмендегідей болады:

Ресурстарды пайдалану туралы есебін төмендегі модель арқылы көрсетеміз:

Берілген есептің ерекшелігі сол, және Р2 , өнімдерін шығару
нұсқалары өте көп, яғни шектеулерді қанағаттандыратын және х2,
шамаларының жиынтығы бірнеше болуы мүмкін. Алайда өнім шығарудың ең көп
табыс әкелетін ғана нұсқасын таңдау керек. Сонда ғана бұл нұсқа оптималды
болады. Есептегі f функциясы және шектеулердің бәрі сызықтық түрде.
Ресурстарды пайдалану есебі сызықтық программалау есебіне жатады және ол
әртүрлі ресурстарды пайдалана отырып әртүрлі өнім шығаратын әртүрлі
өндірісте әртүрде шығарылады. Осы жағдайларды ескере отырып, берілген
есептің жалпы түрін төмендегідей жазып көрсетейік:
Айталық, өндіріс орны п түрлі өнімді т түрлі шектелген ресурстарды
пайдаланады. Келесі шамалар белгілі дейік:
) – i түрлі ресурс қоры;
- j- түріндегі өнімнің бір бірлігіне жұмсалынған i- түріндегі
ресурс көлемі;
- j-түріндегі өнімнің бір бірлігін өткізгеннен түскен табыс
көлемі.
Сатылған өнімнен неғұрлым көп табыс алатындай жоспарды құру қажет.
Обозначим через - арқылы j- түрдегі шығарылатын өнімнің мөлшері .
Олай болса, ресурстарды пайдалану есебінің жалпы түрін төмендегі модель
арқылы бейнелеуге болады:

мұндағы,

1.1.2 Қоспа туралы есеп (Диета туралы есеп).
Ірі қара малын бордақылау үшін екі түрлі К1 және К2 жемдерінен қоспа
жасау керек. Қоспаның бір ірі қара малына арналған бөлігінде нәрлі заттар
берілген: V1–12 бірліктен кем емес, V2–6 бірліктен кем емес, V3-9 бірліктен
кем емес.
Қалған мәліметтер мына кестеде берілген:

Нәрлі заттар Жемнің бірлігіндегі нәрлі заттар мөлшері
К1 К2
V1 3 2
V2 1 2
V3 3 1

Жемнің бірлігінің бағасы: 2 3

Қоспаның құнарлығын сақтай отырып, минималды шығын жұмсалатын жем
қоспасының мөлшерін табу керек.
Модель құруды белгісіздер енгізуден бастаймыз.х1 деп К1 жемінің мөлшерін,
х2 деп К2 жемінің мөлшерін белгідейміз.
Берілген есептің зерттеу объектісіне қоспаны жасау жатады.
Қосылатын шикізаттардың мөлшері мен тағамдық заттардың (белок, май,
көміртегі, т.с.с) өлшем бірліктері әртүрлі болуы мүмкін, мысалы
шикізаттар–т , кг, ал тағамдық заттар –г беріледі.
Зерттеу мақсаты–жемге аз шығын жұмсай отырып, қоспаның берілген
жұғымдылығын қамтамассыз ету.
Есептің критерийі–минималды шығын.
Осы критерийді формула түрінде жазайық.
К1 жемінің бағасы 2теңге, ал мөлшері–х1, ал барлық К1 жемінің бағасы 2х1
теңге болады.К2 жемінің бағасы 3 теңге де мөлшері –х2, сондықтан барлық К2
жемінің бағасы 3х2 теңге.
Екінші жағынан К1 және К2 қоспасының бағасы минималды болғандықтан,
есептің критерийін төмендегідей жазуға болады:
f = 2x1+3x2→ min
есептің берілгені бойынша қоспа үш түрлі нәрлі заттан тұрады және әрбір
нәрлі зат берілген мөлшерден кем болмауы қажет, яғни қоспаның берілген
жұғымдылығын (сапасын) қамтамасыз ету керек. Әрбір нәрлі заттың берілген
мөлшерін пайдалана отырып төмендегідей шектеулерді жазамыз:
3x1+2x2 ≥ 12,
x1+2x2 ≥ 6,
3x1+ x2 ≥ 9.
Қоспадағы жемнің мөлшері оң сан немесе 0-ге тең (егер жемнің бір түрі жоқ
болса). Сондықтан модельде айнымалылардың теріс еместік шарты көрсетілуі
қажет:
х1 ≥ 0, х2 ≥ 0
Берілген қоспа есебінің моделін төмендегідей жазуға болады.
f = 2x1 + 3x2→ min
3x1+2x2 ≥ 12,
x1+2x2 ≥ 6, (1)
3x1+ x2 ≥ 9.
Мұндағы х1 ≥ 0, х2 ≥ 0
Берілген есептің ерекшелігі сол, К1 және К2 жемдерін қосудың бірнеше
нұсқасын, яғни берілген шектеулерді қанағаттандыратын х1 мен х2 мәндерін
көптеп табуға болады. Бірақ бізге ең аз шығын жұмсалатын нұсқаын таңдап алу
қажет. Сол нұсқа қоспасының оптималды нұсқаы болып табылады. Сондықтан
берілген есептің f – мақсат функциясы мен шектеулері сызықтық программалау
есептеріне жатады.
Қоспаның қарастырылған жеке есебін жалпы түрге келтірейік. Жемнің түрі n,
ал нәрлі түрі m болсын. Қоспа бөлігінде і-ші нәрлі заттың мөлшері

bi (i=1.m)- ден кем емес. aij (i=1,m; j=1,n) –і нәрлі заттың j-жемнің
бір бірлігіндегі і мөлшері; Ci (j=1,n) j - жемінің бір бірлігінің бағасы.
xj (j=1,n) – деп j-ші жем мөлшерін белгілейміз. Сонда қоспа есебінің жалпы
түрі мынадай модельмен беріледі :
f=c1 x1+ c2 x2 + ... + cn xn→ min;
a11x1 + a12 x2 +...+ a1n xn ≥ b1,
a21x1 + a22 x2 +...+ a2n xn ≥ b2, (2)
am1x1 + am2 x2 +...+ amn xn ≥ bm,

хj ≥ 0 (j=1,n)
Қосынды белгісін пайдалана отырып (2) есебін төмендегідей жазуға болады.
f=∑ cj xj→ min
∑ aij xj→ b1 (i=1,m)
хj ≥ 0 (j=1,n)
1) және (2) есептерін матрица түрінде де жазуға болады.
Белгілеулер енгізейік: С= (c1, c2,..., cn) – f функциясындағы белгісіздер
коэффиценттері жол – матрица;
b1
B = b2 – шектеулердің бос мүшелерінің
матрица–бағанасы;
...
bm

х1
Х = х2 –белгісіздердің матрица–бағанасы
...
xn

Сонда есептің матрицалық формасы төмендегідей жазылады:
f= Cx→ max,
Ax ≤ B (3)
x ≥0
ал , (2) есебінің түрі:
f= Cx→ min,
Ax ≥B, (4)
х ≥0
Сызықтық программалау есептерінде шектеулер теңдік түрінде де берілуі
мүмкін, ал мақсат функциясы максимумға немесе минимумға шығарылады. Мұндай
есептердің матрицалық формасы
f= Cx→ max (min),
Ax =B, (5)
х ≥0
(3), (4), (5) есептері сызықтық программалаудың жеке түрлері болып
табылады. Олардың ерекшеліктері шектеулері бір ғана түрлі. Осылармен қатар
сызықтық программалау есептерінде аралас шектеулері бар (≤, ≥,= ) есептер
де көп тараған.

1.2 Сызықтық программалаудың жалпы есептері. Негізгі анықтамалар
Сызықтық программалаудың жеке есептерінің моделінен жалпы
модельге көшуге болады
f = ∑ cjxj → max (min),
∑ ai j xj ≤bi (i= 1,m1),
∑ ai j xj ≥bi (i= m1+1,m1+m2),
∑ ai j xj =bi (i= m1+m2+1, m1+m2+m3),
xj ≥0 (j=1,n).
Сызықтық f функциясы мақсат функциясы деп аталады.
Айнымалылардың теріс еместік xj ≥0 (j=1,n) шартынан басқалары
шектеулер деп аталады. Сызықтық программалауда айнымалылардың берілген
шектеулерді қанағаттандыратын кез келген жиыны есептің мүмкін шешімі
(мүмкін жоспары) деп аталады.
Барлық мүмкін шешімдер сызықтық программалау есептерінің анықталу
облысын құрайды. Мақсат f функциясын максималдайтын немесе минималдайтын
мүмкін шешім есептің оптималды шешімі деп аталады.
Егер х*= (х1*,х2*, ... ,хn*) – оптималды шешім болып, х= (x1,x2, ... ,xn)
– кез келген мүмкін шешім болса, онда мына қатынастар дұрыс болады
f (x*) ≥ f (x)– есеп максимумға шығарылса
f (x*) ≤ f (x) – есеп минимумға шығарылса
Ескерту. bi шамасының экономикалық мәніне сәйкес әр уақытта bi ≥ 0
(i=1,m). Ал кейбір есептерде bi 0 болуы мүмкін. Ондай жағдайда bi 0
шектеуінің екі жағын да (-1)-ге көбейтеміз, ол кезде шектеудегі
теңсіздіктің мәні керісінше өзгереді.

1.3 Көлік есебінің математикалық қойылымы

Практикада сызықтық программалаудың жиі кездесетін есептерінің бірі
транспорт есебі. Бұл сызықтық программалаудың біркелкі өнімді
жабдықтаушылардан тұтынушыларға тасып жеткізгенде ең аз шығынжұмсалуын
табатын классикалық есебі. Жаңа шаруашылық жағдайында ,шығындарды өте
жоғары деңгейде қысқартуда , оның ішінде көлік шығынын азайтуда транспорт
есебінің шешімін табу маңызды.
Көлік есебінің жалпы түрін қарастырамыз. А1, А2 , ... , A m , m
жабдықтаушыда біркелкі өнім (жүк) жинақталған және оның жабдықтаушыдағы
мөлшері a1, a 2 , ... Am тең дейік. Осы өнімдерді В1, В2 , ..., Вn n
тұтынушылардың әр қайсысына b1, b2 , ..., bn мөлшерінде жеткізу керек. Әр
жабдықтаушыдан тұтынушыға жүктің жеке бір бөлігін тасымалдаудың шығыны
берілген және ол СiJ - ге тең делік. Сонымен әр тұтынушының қажетін
толық қанағаттандыратын әрі көлік шығыны ең аз болатын жүк тасмалдаудың
жоспарын табу керек. Жабдықтаушыларға – кәсіпорын, склад, баздар, ал
тұтынушыларға – магазин, құрылыс объектілері жатады. Есептің моделін құру
үшін белгісіздерді еңгіземіз. XiJ (i= 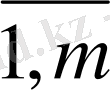, J=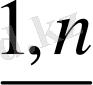) деп I
жабдықтаушысынан J тұтынушысына апаратын жүк мөлшерін белгілеп, берілген
мәліметтерді жоспарлау матрицасы түрінде бейнелейік.

Тұтынушылар Жабдық-
Жабдық- таушылар
таушылар
В1 В2 ... Вn
A1 С12 a1
С11 Х12 ... C1n
Х11 X1n
A2 С21 C22 a2
Х21 X22 ... C2n
X2n
... ... ... ... ...
Cm1 Cm2 C m n
Am Xm1 Xm2 ... X m n am

1.4 Көлік есебінің моделдері

Нақты жүк тасымалдау есептерінде мынадай үш түрлі жағдайдың
бір кездесуі мүмкін:
1. Жабдықтаушылардағы барлық жүк мөлшері () тұтынушылардың тұтыным
мөлшеріне ( ) тең:
a1+a2+ . . . +am= b1+b2+...+b n немесе = (1.1)
Бұндай есепті көлік есебінің жабық түрі деп аталады.
2. Жабдықтаушылардағы барлық жүк мөлшері ; тұтынушылардың тұтыным
мөлшерлерінен үлкен: a1+a2+ . . . +am b1+b2+ . . . +bn
немесе (1.2)
3.Жабдықтаушылардағы барлық жүк мөлшері тұтынушылардың
тұтыным мөлшерінен кем: a1+a2+ . . . +am b1+b2+ . . . +bn
немесе (1.3) . 2 –ші және үшінші формулалар көлік
есебінің ашық түріне жатады.
Осы жағдайлардың әр қайсысына көлік есебінің белгілі бір моделі сәйкес
келеді. a1+a2+ . . . +am= = (1.1)
өрнектелген (І) жағдайды қарастырамыз, көлік есебінің зерттеу объектісі
жүктерді тасмалдауды жоспарлау болып ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.