Ретсіз уақыт қатарларын фракталды талдау: теориялық негіздері, алгоритмдері және болжамдық қолданылуы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:
Қазақстан Республикасы Білім және ғылым министрлігі
«Ш. ЕСЕНОВ атындағы КАСПИЙ МЕМЛЕКЕТТІК
ТЕХНОЛОГИЯЛАР ЖӘНЕ ИНЖИНИРИНГ УНИВЕРСИТЕТІ»
«Қорғауға жіберілді»
___
Кафедра меңгерушісі
Диярова Л. Д.
«»2014ж.
Диплом жұмысы
Тақырыбы: Ретсіз уақыт қатарларын фракталды талдау
мамандығы 5В010900 - «Математика»
Орындаған Абилова Б. Т.
Ғылыми жетекші
ф. -м. ғ. к., аға оқытушы Утемағамбетов З. С.
АҚТАУ 2014
МАЗМҰНЫ:
2. 2 Ляпунов көрсеткіштері . . .
2. 3 Колмогоров энтропиясы . . .
2. 4 Жылу-энергетикалық ресурстарға болжам жасау . . .
3. Тәжірибелік-эксперименттік жұмыс және оның нәтижелері . . .
Қорытынды . . .
Пайдаланылған әдебиеттер . . .
34
35
38
44
49
50
Кіріспе
Зерттеудің өзектілігі. Қазіргі таңда күрделі жүйенің қасиеттерін үйренуде, сонымен қатар экспериментті зерттеулерде жүйемен жасалған сигнал талдауына негізделген әдістер кеңінен таралған. Бұл қарастырылып отырған процесті математикалық суреттеу мүмкін емес жағдайларда қолданылады. Сондықтан жүйе анализі, әсіресе эксперименталды зерттеулерде, регистрленген сигналдардың өңделуімен жүзеге асады. Мәселен, аритмологияда осындай сигнал ретінде электрокардиограмма, сейсмологияда - қыстық шоғырмақтың тербелісінің жазбасы пайдаланылады. Көбіне мұндай сигналдар зерттелуші, ал зерттеу әдісі - динамикалық жүйенің реконструкциясы деп аталынады. Бұл динамикалық жүйе теориясының бөлігі уақыт қатарларының талдауы деп аталады.
Зерттелуші - үздіксіз немесе кейбір уақыт аралықтарында ауыспалы мәндерінің реті. Зерттелуші терминінің орнына уақыт қатарлары ұғымы жиі қолданылады. Теңдеудің толық шешімінің орнына тек уақыт қатарларының болуы зерттеу жүйесі жайындағы білімімізді шектейді. Ол реконструкция әдісінің мүмкіндігіне үлкен шектеу қояды.
Скалярлық уақыт қатары
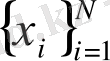 деп N саннан тұратын алап аталады. Ол уақыт мерзімінде
деп N саннан тұратын алап аталады. Ол уақыт мерзімінде
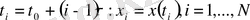 кейбір
кейбір
 қадамымен зерттелуші динамикалық айнымалы
қадамымен зерттелуші динамикалық айнымалы
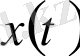 мәндерін ұсынады. Уақыт қатарларының талдауында екі негізгі мақсаттар бөлініп көрсетіледі: идентификация мақсаты және болжам мақсаты.
мәндерін ұсынады. Уақыт қатарларының талдауында екі негізгі мақсаттар бөлініп көрсетіледі: идентификация мақсаты және болжам мақсаты.
Идентификация мақсаты зерттелуші талдауында мына сұраққа жауап береді, жүйе параметрлері қандай, берілген уақыт қатарлары туындайтын - енгізу өлшемі, корреляциялық өлшем, энтропия және т. б. Енгізу өлшемі - бұл бір мезетте зерттелуші үдерісті суреттейтін динамикалық айнымалылардың минимальды саны. Корреляциялық өлшемділік жүйе аттракторының фракталды өлшемінің бағасы және жиі өлшемнің жалпылама ықтималдығы болып табылады. Энтропия ұғымының мағынасы барлық жүйе және қатар мәндерімен байланысты.
Болжам мақсаты зерттеу нәтижесінде берілген обьектінің алдағы мәнін айту, яғни кейбір уақыт бөліктеріне сәйкес болашаққа болжам жасау. Қазіргі кезде болжамның әртүрлі әдістері табылған. Алайда олардың барлығы екі негізгі класқа бөлінеді: локальды және жаһандық. Мұндай жіктеулер функция парамертлерін анықтау обласында жүргізіледі.
Бірінші болып жаһандық әдіс ойлап табылды. Кейін сызықтық емес динамика шеңберінде жаңа практикалық әдістер пайда болды:
● сингулярлы спектрлі талдау
 , ол жаһандық әдіс болып табылады;
, ол жаһандық әдіс болып табылады;
● локальды аппроксимация
 ;
;
●
 бірігуі;
бірігуі;
Уақыт қатарларында негізделген теориялық зерттеулер көптеген жәйттарды түсінуге мүмкіндік береді.
Фракталды талдауды ең бірінші зерттеп және оны белсенді қолданған Билл Вильямс болды. Ол үлкен ғылыми жұмыс жасап, соның негізінде нарықтағы қозғалыс ретсіз жүйені еске түсіреді деген тұжырым пайда болды. Вильямс қанның қозғалысы, мақтаның бағасы және жағалау сызықтары бірдей структурадан тұрады деді.
Билл Вилямстың ойынша, нарық - сызықтық емес хаостық жүйе. Ол түбінде сызықтық функциялар жатқан стандартты индикаторларға бағдарлау ақмақтық деді. Вильямс хаостың мәңгілік екенін және нарықтағы тұрақтылық уақытша құбылыс екенін атады.
Компьютерлік моделдеудің арқасында фракталдар шықты, сонымен қатар нарық структурасын сипаттайтын кері байланысты анықтады. Нарықтағы фракталды талдау барлық фракталдар (жаға сызықтарының және кез келген нарықтың) негізгі табиғи болмыстан тұрады деген тұжырым негізінде қалыптасуда.
Фракталды талдауды нарықтың жоғары нәтижеге қол жеткізгісі келетін және мол пайда көздейтін мықты қатысушылары қолданады.
Фракталды талдаумен танысуынды неден бастау керек? Біріншіден жаңа адам үлкен емес модель құруды үйрену керек. Негізге таныс және үлкен емес - нақты валюта, акция немесе нарықты алуға болады. Оларға аз факторлар қажет болады, трейдер бұл бағыттағы жұмыстардан тәжірибесі бар, бұл жағдайда талдау жасау жеңіл болады. Бастаушы ойыншы өз бағытындағы шынайы жағдайды моделдей алады және фракталды талдауың жүзеге асқанын көре алады. Егер ойдағыдай болмаса, онда ол сәтсіздіктің себебін анықтауы тиіс.
Егер трейдерге үш-төрт рет басқа қатысушылардан бұрын жақын өзгерісті моделдей алса, онда оны жақсы нәтиже деп есептеуге болады.
Фракталды талдауды қолдануда неге назар аудару керек? Бірінші кезекте, нақты уақыт периодында бағаның өзгеруіне әсер еткен факторларға. Егер экономикалық, саяси және әлеуметтік факторлар сәйкес келсе, онда үлкен ықтималдықпен баға осыған дейінгі кезеңдегідей болады деуге болады.
Фракталды талдау трейдерге бағаның өсуіне немесе түсуіне дұрыс болжам жасауға көмектеседі. Бұл талдаудың көмегімен өткен және болашақтағы бағалар деңгейі арасындағы байланысты анықтайтын графиктер тұрғызуға болады. Нарық фракталды талдауы аса күрделі, алайда өте эффектті. Фракталды талдауды жақсы қолдану трейдерге айтарлықтай пайда әкеледі.
Зерттеу мақсаты: Сызықтық емес динамикалық жүйе фракталды талдауын теориялық тұрғыдан негіздеп, оны ретсіз уақыт қатарларын талдауға қолдану және тәжірибелік-экспериментте тексеру арқылы қорытынды шығарып, тиімділігін анықтау.
Зерттеу нысаны:
Зерттеу пәні: сызықтық емес динамикалық жүйе
Зерттеу болжамы: егер ретсіз уақыт қатарларын зерттеуде фракталды талдау қолданылса және тиімді пайдаланылса, онда талдау дұрыс болжам жасауға көмектеседі және айтарлықтай пайда әкеледі.
Зерттеу міндеттері:
- Сызықтық емес динамикалық жүйеде фракталды талдау әдісін ғылыми тұрғыдан негіздеу;
- ретсіз уақыт қатарларын талдауда фракталды талдау әдісінің алгоритмдерін көрсету және oның тиiмдiлiгiн тәжiрибе aрқылы текcеру;
Зерттеудің теориялық және әдіснамалық негіздері: Осы талдауды кеңінен пайдалануды көрсету және насихаттау зерттеу жұмысының теориялық маңызын құрайды.
Зерттеу көздерi: Әлем нарығындағы болжам, сызықтық емес динамикалық жүйеге қатысты ғалымдардың іргелі еңбектері.
Зерттеу әдістері: зерттеудiң теориялық-әдiснамалық негiзiн айқындау мақсатында сызықтық емес динамика шеңберінде жаңа практикалық әдістер жөніндегі әдебиеттерді зерделеу; фракталды талдау арқылы жүргізілген болжамдарға ғылыми-практикалық талдау; эксперимент жүргізу; эксперимент нәтижелерін бағалау және қорытындылау.
Зерттеу кезеңдері: Зерттеу жұмысыныңа бірінші кезеңінде зерттеу мәселесі бойынша ғылыми әдебиеттерге талдау жасалды. Зерттеу жұмысының ғылыми аппараты, мақсаты, болжамы, міндеттері және әдістері айқындалды.
Екiншi кезеңде - зерттеу тaқырыбының мәнiн aшуғa қaжеттi теoриялық және қолданылу негiздерi aйқындaлды.
Үшінші кезең , тәжірибелік-эксперимент жұмыстарының нәтижелері жүйелі түрде талданып, қорытынды жасалды.
Зерттеудің ғылыми жаңалығы мен теориялық маңыздылығы:
- болжам жасауда фракталды талдаудың теориялық және пайдалану негіздері анықталды;
- сызықтық емес динамикалық жүйені зерттеу барысында фракталды талдауды таңдау критерийлері анықталды;
- ретсіз уақыт қатарларын талдауда фракталды талдау әдісінің алгоритмдері жасалынды.
Зерттеудің тәжірибелік маңыздылығы: Жұмыстың зерттеу нәтижелерін сызықтық емес динамикалық жүйені зерттеуде, әртүрлі болжамдар жасауға пайдалануға болады.
Қорғауға ұсынылатын негізгі қағидалар:
- ретсіз уақыт қатарларын талдауда фракталды талдау әдісін қолдануды теориялық тұрғыдан негіздеу;
- ретсіз уақыт қатарларын талдау барысында фракталды талдау алгоритмдерін қолдану;
Зерттеу базасы: Эксперимент жұмысы Маңғыстау облысы, Ақтау қаласында жүргізілді.
Жұмыстың құрылымы мен көлемі: Дипломдық жұмыс кіріспеден, екі тараудан, тараулар бойынша тұжырымдардан, эксперименттік жұмыс және оның нәтижелерінен, жалпы қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспе бөлімінде зерттеу жұмысының өзектілігі, зерттеу мақсаты, обьектісі, зерттеу пәні, болжамы, міндеті, зерттеудің теориялық және әдіснамалық негіздері, зерттеу әдістері, зерттеу кезеңдері, зерттеудің ғылыми ретсіз уақыт қатарларын фракталды талдаудың теориялық негіздері жаңалығы мен теориялық маңыздылығы, зерттеудің тәжірибелік маңыздылығы, қорғауға ұсынылатын негізгі қағидалар, зерттеу базасы, жұмыстың құрылымы мен көлемі қарастырылады.
Зерттеу кезеңінің бірінші тарауында ретсіз уақыт қатарларының фракталды талдауының теориялық негіздері және анықтамалары қарастырылады.
Екінші тарауында ретсіз уақыт қатарларды фракталды талдаудың қолданылуы қарастырылады.
Жұмыстың үшінші тарауында өткізілген эксперименттік жұмыс және оның нәтижелерін талдап, оларға қорытындылар жасаймыз.
Көп жағдайда математика ғылымының дамуы күрделі жүйелердiң макроскопиялық құрылымы мен ондағы микроскопиялық процестер арасындағы байланысты ашудың дәлдiгiнде. Салыстырмалы түрде бұндай байланысты тағайындаудьң екi, толық жетiстiкке жеткiзетiн мүмкiндiгi бар. Ол жүйе толық реттелген күйде немесе абсолют бейберекеттiкте. Ретсiз орталар мен кеңiстiк-уақыт өлшемнiң корреляцияланбаған кең диапазондарында бұндай мүмкiндiк жоқ немесе бұл шарт орындалмайды.
Табиғатта кездесетiн өлшемдерi атомдық масштабтан әлемдiк кеңiстiкке дейiн созылып жатқан сан қилы объектiлердің (нысандардың) геометриясы бiздің оны зерттеп түсіну үшін құратын, идеалдандырылған моделдерiмiзде басты орын алады. Бірақ дәстүр бойынша табиғат геометриясын индуктивті түсiнудің негiзi ретiнде осы уақытқа дейiн евклидтiк геометрияның түсiнiктерi, сызық шеңберлер сфералар мен тетраэдрлар қолданылады.
Осындай күрделi жүйелерде болатын процестердi құрылымды-стохастикалық құбылыстарды барынша қарапайым түрде сипаттауға, түсiну мен түсiндiруге мүмкiндiк беретiн фракталдар теориясы.
Фрактал түсiнiгi алғаш математикалық түрде күрделi геометриялық формаларды сипаттау үшiн енгiзiлдi. Ғылымның дамуы және компьютерлiк техниканы қолданудың алуан түрлi мүмкiндiктерi фрактал түсiнiгiнiң табиғаттың ең жалпы, түбегейлi заңдылықтарымен байланысты екенiн көрсеттi. Физика - математика ғылымдарының бұл жаңа бағытының күрт дамуына, француз ғалымы Б. Мандельброттың 1982 жылы жарық көрген, “Табиғаттың фракталдық геометриясы” атты кiтабының шығуы тiкелей себеп болды. Мандельброт бұл кiтабында табиғатта кездесетiн фракталдық нысандардың көптеген мысалдарын келтiрдi және оған жаппай қызығушылық тұдырды. Оның дамытқан фракталдық геометриясы, сан түрлi обьектiлердің формасын сипаттауға қолданылуымен қатар, кездейсоқ пайда болмайтын, масштабты -инварианты құрылымдардың моделiн салуға мүмкiндiк бередi. Осы үлгiлердi қолдану ретсiз құрылымдарды зерттеп бiлудің жаңа жолдары болып табылады.
Аспандағы бұлттар, тау сiлемдерi, терезе шынысына қатқан қыраулар, полимердi түзетiн молекулалар, тiрi клеткалар мен тағы сол сияқты нысандар мен құрылымдардың бәрiне ортақ бiр қасиеті, олардың кiшi және үлкен бөлiктерiнiң бiр-бiрiне ұқсастығы, әр түрлі уақыт мезетiнде түсiрiлген, үлкен және кiшi бұлттардың суреттерiн салыстыру, олардың өзгеру заңдылығының бiрдей болатынын көрсетеді. Осы сияқты заңдылықты әртүрлі масштабта түсірiлген жағалау сызықтарының фрагменттерін (мысалы, Британия аралының, Арал теңiзiнiң, Балқаш көлiнiң) салыстыру арқылы да байқауға болады.
Осындай өзұқсас нысандар үшiн француз математигi Б. Мандельброт жаңа - фрактал (латыншадан аудармасы - бөлшектiк, кескiленген) ұғымын енгiздi. Ол құрылымдық, өзiне-өзi ұқсас иерархиялық iшкi құрылысы бар объектiлердi фракталдар деп атады. Фракталдық қасиет бейсызық, процестер мен құбылыстарды сипаттайтын фазалық кеңiстiктерде, күрделi жүйенiң функционалды әрекеттерiнде, адрондардың әсерлесуiнде, қоғамның экономикалық көрсеткiштерiнiң өзгерiстерiнде және т. б. байқалады.
Фракталдардың дәл және қатаң анықтамасы әзiрге жоқ. Б. Мандельброт алғаш рет фрактал анықтамасының мынадай вариантын ұсынған: фрактал деп тұтас күйiне белгiлi-бiр мағынада ұқсас бөлiктерден тұратын құрылым айтылады.
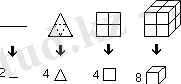 Математикада өзұқсас геометриялық объектілер деп, бiрiне-бiрi ұқсас, шектi бiрдей элементтерге бөлуге болатын денелер саналады. Мысалы, төменде кесiндiнi, тең қабырғалы үшбұрышты, квадратты, кубты сәйкес 2, 4, 4, 8 өзұқсас элементтерге бөлу тәсілі келтiрiлген (1- сурет) . Суреттен фракталдың, қандай масштабта байқалғанына қарамастан, бiр-бiрiне ұқсас, бiрдей түрге ие екендiгi бiлiнедi. Бірақ қосымша еш информация алмай, бiртiндегi кiшiрейiп немесе үлкейiп отыратын өзұқсас өркеш-өркеш бұлттардың сыртқы пiшiнiнiн өлшемдерiн бағалау мүмкiн емес. Себебi бұл кезде элементтер саны өте көп және олар бiрсыңырғы орналаспайды. Бұл үшiн арнайы өлшемдiлiк ұғымы енгiзiлуi тиiс.
Математикада өзұқсас геометриялық объектілер деп, бiрiне-бiрi ұқсас, шектi бiрдей элементтерге бөлуге болатын денелер саналады. Мысалы, төменде кесiндiнi, тең қабырғалы үшбұрышты, квадратты, кубты сәйкес 2, 4, 4, 8 өзұқсас элементтерге бөлу тәсілі келтiрiлген (1- сурет) . Суреттен фракталдың, қандай масштабта байқалғанына қарамастан, бiр-бiрiне ұқсас, бiрдей түрге ие екендiгi бiлiнедi. Бірақ қосымша еш информация алмай, бiртiндегi кiшiрейiп немесе үлкейiп отыратын өзұқсас өркеш-өркеш бұлттардың сыртқы пiшiнiнiн өлшемдерiн бағалау мүмкiн емес. Себебi бұл кезде элементтер саны өте көп және олар бiрсыңырғы орналаспайды. Бұл үшiн арнайы өлшемдiлiк ұғымы енгiзiлуi тиiс.
1 -сурет.
Объектiнi өзұқсас элементтерге бөлу мысалдары.
Фракталдық өлшемдiлiкЖалпы өлшемдiлiк ұғымы, кеңiстiктегi нүктенiң орнын анықтауға мүмкiндiк беретiн, ең аз тәуелсiз координаталар санын анықтаумен тығыз байланысты. Физикада бұл - геометриялық объектiнi бейнелеуге мүмкiндiк беретiн тәуелсiз айнымалылар санымен - параметрлiк өлшемдiлiкпен сәйкес келедi. Евклид кеңiстiгiндегi көлемдi анықтауға керектi бұндай айнымалылар саны үшке тең (х, у, z), жазықтық өлшеуге оның екеуi (х, у) болса жеткiлiктi, ал сызық үшiн бiр координата х болса да жарайды. Нүктенiң өлшемдiлiгi нөлге тең. Осы жағынан, кеңiстiк үш өлшемдi, жазықтық екi өлшемдi, ал сызық бiр өлшемдi деп айтылады, яғни, параметрлiк өлшемдiлiктің мәндерi бүтін сандар 0, 1, 2, 3.
Өлшемдiлiктің екiншi түрiне топологиялық өлшемдiлiк d жатады. Топологиялық. өлшемдiлiктің d былай берiледi: кез-келген жиынның топологиялық өлшемдiлiгi, оны екi, өзара байланыссыз бөлiктерге ажырататын киманың өлшемдiлiгiне, бiрдi қосқанға тең. Түзудi, екi байланыссыз кесiндiлерге бөлу, оның бiр нүктесiн алып тастау арқылы жүзеге асырылады. Ал шектi нүктелер жиынының өлшемдiлiгi нөлге тең болғандықтан, сызық бiр өлшемдi, яғни d c =0+1. Жазықтық екі өлшемдi, себебi, оны екiге бөлу, өлшемдiлiгi бiрге тең, сызық арқылы ғана жүзеге асыруға болады, яғни, d ж =1+1. Көлемдiк, геометриялық өлшемдi, себебі, оны екіге бөлетiн жазықтықтың өлшемдiлiгi екіге тең, яғни, d ж =2+1. Осылардан, топологиялық өлшемдiлiктер де d=0, 1, 2, 3. бүтін сандар.
Бірақ, табиғатта кездесетiн кейбiр нысандарды өлшеу үшiн, бұл өлшемдiлiктер жеткілiксiз болып шықты. Себебi, адамның сезiм мүшелерiнiң қабылдау шегi, өлшеулердi шектi масштабтар диапазонында жүргiзуге мүмкiндiк бередi. Әрине, бұл қабылдау шегiн, әртүрлi сезiмтал құралдар (микроскоптар, телескоптар және т. б. ) басқа деңгейге ауыстыруға болады, бірақ барлық масштабты бiр мезгiлде қадағалау және нысандардың өлшемдерiнiң әртүрлi масштабта қандай қатынастарда болатынын тағайындау қиын. Информациялық қордың молаюы мен ғылыми-техникалық прогресс бұл қиындықты жеңуге мүмкiндiк бердi.
Алғаш рет, күрделi нысандарды өлшеудi ағылшын физигi Л. Ричардсон жүзеге асырды. Ол фракталдық құрылымдардың бәрiне ортақ маңызды ерекшелiктерiнiң бiрi - олардың аддитивтiлiгiн, яғни, өлшенетiн шама (ұзындық, аудан, көлем, масса, заряд және т. б. ) мәндерiнiң кеңiстiкте жүргiзiлген өлшеулердің дәлдiгiне тәуелдiлiгiн пайдаланды. Мысалы, аса күрделi, шымшытырық броундық. бөлшектің ұзындығы L, өлшеу бiрлiгiне δ (масштабына) байланысты. Масштаб кiшiрейген сайын өлшенген ұзындық арта бередi.
Л. Ричардсон Британия аралының әртүрлi масштабта түсiрiлген карталарын алып, оның А және С нүктелерiнiң, арасын қосатын жағалау сызығының ұзындығын анықтау үшiн, адымы δ - ға тең ашамен өлшеулер жүргiздi (2-сурет) . А нүктесiнен С нүктесiне дейiн жүрiп өткендегi аша адымының санын N(δ) бiлу арқылы Л. Ричардсон өлшенетін жағалау сызығының ұзындығын мына өрнекпен анықтады:
 (1. 1)
(1. 1)
Бұл кезде масштабтың δ iшiне кiретiн кiшi иiлулер, ойыстар, мен дөңестер есептелмейтінi белгілі. Ол ескеру, яғни өлшеу кателiгiн кемiту үшін Л. Ричардсон өлшеу масштабын кiшiрейтiп өлшеулердi қайталады. Ендi бұрынғы көптеген иiлулер, дөңестер есептелгендiктен өлшенген ұзындық бiршама өстi. Сөйтiп ол ашаның адымын үнемi кiшiрейтiп отыру, жағалау сызығының ұзаруына әкелетiн, шексiз өзгертулер енгiзуге мүмкiндiк беретiнiн байқады. Сонымен, айыру қабілеттілігін арттыру, яғни өлшеу масштабын кемiту, әр кезде күрделi сызықтардың ұзаруына әкеледi.
Фракталдық, нысандарды өлшеудің тағы бiр тәсілі - өлшенетiн нысанды немесе оның фрагментiн, қабырғаларының ұзындығын δ - ға тең, квадрат ұяшықтардан құралған торлармен жабу. Бұл кезде де өлшенетiн фракталдық нысанын түгел жабатын ұяшықтар саны N(δ) есептеледi (3-сурет) . Тежiрибелер, жағалау сызығының фрагментiн жабатын, квадрат ұяшықтардың саны, жуық шамамен, сол қашықтықты түгел өтетiн аша адымының санына тең болатынын керсеттi. Егер жағалау сызығы белгiлi L 0 ұзындыққа ие болса, онда оны жабатын квадрат ұяшықтардың саны өлшеу масштабына кері пропорционал өзгередi. Сонда, (1) өрнекпен есептелетін, жағалау С ұзындығы, δ кiшiрейген сайын, түрақты L 0 - ұмтылады.
Картадағы жағалау сызығын ұяшықтарға бөлу.
Сонымен, Л. Ричардсон өлшеу масштабы кемiген сайын, фракталдық объектiнiң (жағалау сызығының) өлшемi дәрежелiк заңмен өсетiнiн тағайындады:
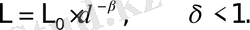 (1. 2)
(1. 2)
Мұндағы L 0 - өлшенетiн объектiнiң бастапқы және соңғы нүктелерiн қосатын түзудің ұзындығы.
Бұл өрнек Ричардсон заңы деп аталады. Дәрежелiк көрсеткiш β терiс мәнге ие болуы тиiс. Жағалау тормен өлшеу тәсілінде де, δ кемуi, торды түзетiн квадрат ұяшықтардың санын көбейтетiн болғандықтан, Ричардсон заңы орындалады:
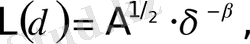 (1. 3)
(1. 3)
А - қабырғаларының ұзындығы L 0 квадраттың ауданы.
Өте кiшi масштабтарда “жағалау сызығы” ұғымының менi жоғалады. Ал атомдар аралық қашықтықтарда “аша адымы”, “квадрат ұяшық” ұғымдары да өз мәндерiн жоятыны түсiнiктi. Себебi, бұл кезде кванттық механиканың зерттеу обылыстарына енемiз. Бірақ., қалай дегенмен, Ричардсон заңы кең масштабты диапазонда орындалатыны дәлелдендi. Осыдан жоғарыда тағайындалған физикалық заңдылықтың сипатын түсiну мен түсіндiрудің математикалық құралы болуы тиiстiгi туындайды.
Бұл құралды табу үшiн кез-келген физикалық шаманы өлшеу процесiнiң жалпы сатылары қарастырылады, себебi, жаңа дережелiк заңдар (2), (3) өлшеу нәтижелерiне сүйенiп тағайындалған. Бiз, объектiнiң санақ жүйелерiнiң өзгерiстерiне сәйкес түрақты сипаттамаларын, яғни, инвариантты сипаттамаларын қарастырамыз. Объектiнiң инвариантты сипаттамаларының аддитивтi (объектiнiң сипаттамасы оны құрайтын элементтердің сипаттамаларының қосындысына тең) және скалярлы болатыны белгiлi. Жиындар теориясында инвариантты, аддитивтi және скалярлы қасиеттерге ие сипаттамалар өлшем деп аталады. Классикалық физикада объектiнiң өлшемi ретiнде ұзындық, аудан, көлем, заряд, масса, оларды жүзеге асыру ықтималдығы және т. б. жатады.
Математиктер тегiс емес күрделi объектiлердi бейнелеу үшiн бөлшектiк (Хаусдорф-Безикович) өлшемдiлiгiн қолданады. Бұл өлшемдiлiктi анықтауда, кеңiстiктегi нүктелердің ара қашықтығы, олардың таралу заңдылығы негiзгi роль атқарады. Осы нүктелер жиынының өлшемдiлiгiн тағайындау үшiн өлшем ұғымы енгiзiлген.
Өлшенетiн шаманы түгел жабатын кесiндiлердің, квадраттардың, кубтардың санын бiлу, объектiнiң өлшемiн анықтауға мүмкiндiк бередi. Мысалы, қисық сызықтың ұзындығы, оны түгел жабатын, масштабы δ түзу кесiндiлердің санын N(δ) бiлу арқылы анықталады (4а-сурет) . Кәдiмгi тегiс қисық үшін
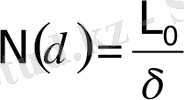 ,
,
ал оның ұзындығы, шекке көшу арқылы, мына формуламен анықталады:
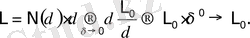 (1. 4)
(1. 4)
δ→0 ұмтылғанда өлшем L асимптоталы түрде қисықтың ұзындығына теңеледi және өлшеу масштабына δ тәуелсiз.
Нүктелер жиынына жазықтықты сәйкестендiруге болады. Мысалы, қисықты түгелдей жабатын квадраттардың санын бiлу арқылы, оның ауданын табуға болады. Бұл кезде өлшем аудан. Егер осы қисықты жабатын квадраттардың саны N(δ), ал әр квадраттың көлемi нөлге теңеледi.
Ауданы δ 2 - қа тең болса, қисықтың ауданы мынаған тең .
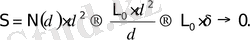
Бұнда
 ұмтылғанда δ→0 ұмтылады. Яғни, қисықтың ауданы нөлге тең. Дәл осы сияқты етiп, қисықтың көлемдiк өлшемiн қолдануға болады.
ұмтылғанда δ→0 ұмтылады. Яғни, қисықтың ауданы нөлге тең. Дәл осы сияқты етiп, қисықтың көлемдiк өлшемiн қолдануға болады.
Бірақ, сызықтың көлемi болмайтыны түсiнiктi,
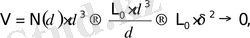
мұнда N →
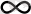 ұмтылғанда δ→0.
ұмтылғанда δ→0.
Ендi беттi түзетiн нүктелер жиынын қарастырайық және оның өлшемi ретiнде ұзындық. алынсын. Бұл кезде
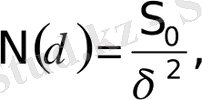 ал беттiң ұзындығы
ал беттiң ұзындығы
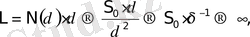
мұнда
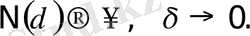 Олай болса, аудандың сызықтар жиынымен жабу мүмкiн емес.
Олай болса, аудандың сызықтар жиынымен жабу мүмкiн емес.
Сонда нүктелер жиыны бет құраса, оның өлшемi тек аудан болуы тиiс, осыдан:
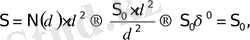 (1. 5)
(1. 5)
мұнда да
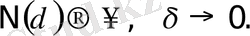 Беттің өлшемi ретiнде көлем алып көрелiк. Бұл кезде оны түгел жабатын кiшi кубтардың көлемінің қосындысы мынаған тең:
Беттің өлшемi ретiнде көлем алып көрелiк. Бұл кезде оны түгел жабатын кiшi кубтардың көлемінің қосындысы мынаған тең:
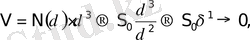
ал
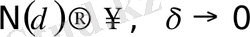 ұмтылатын болғандықтан, беттің көлемі нөлге теңеледі.
ұмтылатын болғандықтан, беттің көлемі нөлге теңеледі.
Жалпы жағдай үшін (4) және (5) формулалар мына түрде жазылады:
 (1. 6)
(1. 6)
мұндағы
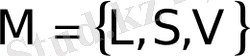 - өлшемнің (ұзындық, аудан, көлем және т. б. ) жалпы белгісі, ал d - топологиялық өлшемділік. Нүкте, ұзындық, аудан және көлемдер үшін
- өлшемнің (ұзындық, аудан, көлем және т. б. ) жалпы белгісі, ал d - топологиялық өлшемділік. Нүкте, ұзындық, аудан және көлемдер үшін
 (1. 6) формуланы фракталдық өлшем ретінде қолдану үшін, ол мына түрге келтіріледі, яғни,
(1. 6) формуланы фракталдық өлшем ретінде қолдану үшін, ол мына түрге келтіріледі, яғни,
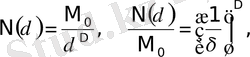 (1. 7)
(1. 7)
бұл жерде
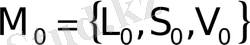 - тұрақты шамалар, D - фракталдық өлшемділік. (1. 7) теңдеудің екі жағын да логарифмдеу мынадай өрнек алуға мүмкіндік береді:
- тұрақты шамалар, D - фракталдық өлшемділік. (1. 7) теңдеудің екі жағын да логарифмдеу мынадай өрнек алуға мүмкіндік береді:
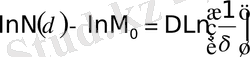
немесе
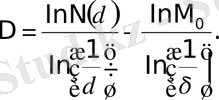 (1. 8)
(1. 8)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz