Оптиканы оқытуда линзалар мен лупаның рөлі және геометриялық оптика негіздері


Мазмұны
І . Кіріспе
1. 1 Оптиканы оқытуда линзаның қажеттілігі.
ІІ . Негізгі бөлім
2. 1 Оптикалық құрал - лупа.
2. 2 Жарықтың сфералық беттен сынуы және линзаның
теңдеуі.
2. 3 Призмадағы сәуле жолы.
2. 4 Линзаның жинауы мен шашырауы.
2. 5 Микроскоп пен телескоп.
ІІІ . Қорытынды
Кіріспе
Физика - қазіргі заманғы техниканың ғылыми негізі. Электроника, автоматика, радиотелетехника және техниканың басқа да көптеген салалары физиканың сәйкес бөлімдерінен өрістеп дамыған.
Ғылым мен техниканың (технологиярың) дамуы физика жетістіктерінің техника мен өндірістің түрлі салаларына терең енуіне әкеліп соқтырады. Соған орай физика курсын оқыту және оны меңгеру қоғамның әрбір мүшесіне қажетті бола түсуде. Қазіргі мектептер мен жоғарғы оқу орындары өміріндегі өскелең талаптар осыны көздейді.
Физиканың үлкен бір саласы - оптиканы пән ретінде оқытудың соншалықты маңызды екенін айтып жатудың кажеті жоқ. Өйткені, оптиканы оқыту ғылымының түбегейлі түсініктері мен түйіндерінің түп негіздерін терең түсінуге, техниканың тетігін тез үйренуге дайындықты дамыта түседі.
Тегінде оқушылар да, жалпы оқырман да оптиканы айтқанда жарық беретін кәдімгі шамды, көз әйнекті, фотоаппаратты, концерт сарайларының сахнасын сан кұлпыртып тұратын панарларды, микроскопты, телескопты, фототелеграфты, теледидарды, телеорталықты, талшықтар оптикасын, лазерлер мен голографияны және т. б. таңғажайып техниканың туындыларын елестетеді.
Бұрыннан колдалынып келе жатқан оку бағдарламасыңда оптиканы оқытуға 36 сағат бөлінген. Ал физиканы тереңдетіп окытатын мектептер мсн арнайы сыныптарда сабақ 56 - 72 сағат төңірегінде жүргізуге есептелінеді. Қазіргі техникалық лицей, гимназия, физика - математикалық мектептерде оптиканы оқытуға арналған сағат саны одан көп болып отыр.
Ал бүгінгі күннің ағымын аңғарған жаңа түрдегі мектептерде оптиканың жаңа салаларын оқытуға көбірек көңіл аударылып отыр. Әлі оқу бағдарламасын толықтыра түсіп жатқан атағы да бар.
Ежелгі әдет бойынша оптиканы оқыту - геометриялық оптиканы оқытудан басталады. Оның бірінші себебі - геометриялық оптиканың, қала берді бүкіл физиканың бұрынғы заманнан келе жатқан ежелгі де ескі саласы. Екіншіден, геометриялық оптиканың оқытатын заңдары мен заңдылыктары, теория мен тұжырымдары табиғи танымдылығымен етене-таныс түсініктердің түп негізіне айналған. Үшіншіден, геометриялық оптиканың кейбір заңдылыктары мен ережелерінің елеулі мөлшері табиғаттың тап өзінен табылып, бір физикалық құбылыстардың тылсымының тұңғиығымен де тұп-тура таныстырып та тиімдік тудырып жүр. Тіпті оларды қолдануға да қолайлы жағдай жасап отыр. Мысалы, ежелгі ерте дүниеден белгілі кәдімгі жарық шоғын жинайтын линзаны, алайықшы. Оның өте қарапайымдылығы, колдану үшін қосымша бірде-бір керек-жарақтың қажет еместігі, тіпті арнайы білімнің керек еместігі кімді болса да таңырқатпай коймас. «Әйгілі Архимед оптикалық линзаны колданып Күн сәулесінің шоғын шоғырландырып, жаудың кемесін жағып жіберіпті дегенде аңыз әңгіме бар».
Келесі кезекте оқылатын оптика саласы ол - физикалық оптика. Оған оптикалық кұбылыстар мен табиғаттан табылып, жаратылыста жаңарып «жасалып» жатқан барлық үрдістер мен өзгерістердің физикалық ішкі мән-мағынасын, тұңғиық тылсым сырын ашу сияқты ең мәртебелі мәселелер жатады. Ол - жарық толқындарының интерференциясы, дифракциясы, дисперсиясы жәнс жарық шоғының тарауы мен шашырауы, жарықтың кванттық касиеті, фотоэффект құбылысы, жарық сәулесінің түсіретін қысымы т. б. Басқаша айтқанда жарықтың жаратылысының барлық «жақтары» және жарықтық жалпы жаратылыспен әсерлеуіндегі жарастығының жай-жапсарын жатықтау десе де болады.
Кейбір әдістемелік әдебиеттерде оптиканы оқытудың бірнеше жолы қолданылып жүр. Соларды талдап көрелік.
I. Олардың ішінен геометриялық, оптиканың заңдары арқылы кескіндерді шығарып алу, сәуле шоғы, ал жарық көздерін кәдімгі нүкте деп есептеп қарастыру нәтижесінде туатын оқыту әдісін ерекше атауға болады. Геометриялық оптиканы осылайша қарастырып өткеннен кейін жарықтың толқындық және кванттық қасиеттері қарастырылады. Бұл көптен қолданылып келе жатқан көне әдіс.
II. Геометриялық оптикада жарық шоғы түсінігін пайдаланудың шектеулі екендігі ескеріліп отырылатын әдістіде атау жөн.
III. Алдымен сәуле шоғы ұғымын пайдаланудың мүмкіндігі белгілі бір шарттардан аспайтындығы қатаң ескеріліп барып оны геометриялық оптикада қолданады. Сонан соң ғана геометриялық оптика заңдарының қолданылу шегі айғақталады.
Іс-жүзілік тәжірибелер - оқыту барысында екі бірдей идеяны қосарландыра қатар жүргізудің ең тиімді әдіс екенін көрсетті. Яғни, өмірде күнде кездесетін, тікелей тұрмыста ұштастырылып іске асып жүрген кәдімгі ақ жарық сәуле шоғы - тұра толқындар болуы керек деген идеялар қосары қолданылуы керек.
Мұндағы сәуле шоғы ұғымы - шектеулі жарық ағымының өзегі ретінде есептеледі, әрі ол жарықтың тарау бағытын көрсетеді.
Бірақ, оптикалық құбылыстарды оқыту, ашып айтқанда, жарықтың түзу сызықтық таралуын, жарық сәулесінің шашырау және сыну заңдылықтарын, жазық сфералық айналардағы және линзалардағы сәуле жолдарын қарастыру осы арнайы ұғым ретінде алынған сәуле шоғы арқылы зерттеледі.
Геометриялық оптиканың жеке өзін пайдалану арқылы кез келген дененің оптикалық кескінін алуға болады. Бұл геометриялық оптиканың ұтыс әкелетін бір жағы және де, кейбір мектептерде оптикалық құралдардың жетіспеуіне байланысты көзбен көріп, істеп көрмеген лабораториялық жұмыстардың сызбасын геометриялық заңдылықтарға сүйене отырып сызу арқылы түсінуде рөлі ерекше. Бірақ оның есесіне геометриялық оптика сол геометриялық оптиканың өзінің кескінін шығарып беру кезіндегі байқалатын ахроматизацияның, яғни түстің түрленіп - жойылу туу себебін, сол сияқты оптикалық аспаптардың айғақтау «қабілетін» (разрешающая способность) түсіндіріп бере алмайды.
Бізге әрине геометриялық оптиканың негізгі ұғымдары - жарық сәулесі және сәуле шоғы ұғымдарының анықтамасын нақтылы беру керек. Олардың пайдалану шектерін талдап - сипаттау шарт. Әрі іс-жүзінде, тікелей тәжірибеде, осы сәуле мен шоқты бірден алуға бола ма деген мәселені қарастыру да үлкен маңыз атқарады.
Әрине, іс-жүзінде сәуле шоғын алу онша қиындық туғызбайды. Оның толып жатқан мысалын атап, көрсете де аламыз. Ал сәулені (геометриялық, оптикада қолданылатын жіңішке түзуді) алу іс-жүзінде еш мүмкін емес. Оған заманымыздың тамаша оптигі Р. В. Поль айтқандай: «Жарық сәулесін біз тек ақ қағазда ғана көре аламыз» - деген сөзі дәлел.
1. 1. Оптиканы оқытуда линзаның қажеттілігі.
Шынында да, қолымызда тұрған қарапайым нәрседе қаншама ғажап құбылыстар «құлпырып» тұрғанын біз әрқашанда аңғара білеміз бе? Линзаның «күш-құдіреті» оның сырт пішінінде екенін таныстыра білдік пе?
«Линза» термині өзінің «бұршақ тәрізді» сыртқы көрінісіне сәйкес аталып кеткенін, ал лупаның да дәл сол сияқты өзінің сыртқы көрінісіне сәйкес аталып кеткенін ескерткенбіз. Бұл жерде терминдерді айтып отырғанымыздың үлкен мәні бар.
Біріншіден, «линзаның» да, «лупаның» да кәдімгі қарапайым әйнектен немесе басқа бір жәй пластмассалық мөлдір нәрседен жасалатындығы, олардың жарық шоғын жинайтын ғажап қасиеті олардың сыртқы пішініне ғана байланысты ерекшелігі екен.
Екіншіден, керек болса кейде сыртқы пішінінің де сапаға айналу «кереметі» де көпе көрнеу көрініс беріп тұр. (Санның сапаға айналатынын дәлелдейтін философиялық, ұғымды еріксіз еске түсіреді. ) Ал, линзаның оптикадағы, оның ішіндегі сәулелік оптикадағы орны орасан зор.
Қысқасы, линзаның ғажап қасиеті оның сыртқы пішініне байланысты болды. Олай болса, линза қандай пішінде болғанда мұндай ғажап қасиет пайда болатынын білу міндетті шарт шығар.
Іс-жүзінде қолданылатын линзалардың сырт пішіні дөңес болуы немесе ойыс болуы қажет. Дөңес немесе ойыс болғанда да линзаның дөңестенуі мен ойыстануы үздіксіз түрде жалғаса беруі тиіс. Дөңес және ойыс линзаның дөңестігі мен ойыстығы сфералық немесе цилиндрлік беттің бөлігі болуы тиіс. Қысқасы, дөңес ойыс линзалардың өзіне түскен жарық шоғын жинау немесе шашырату сияқты ғажап қасиеті оның сфералық, бет болып жасалуына байланысты болып шықты. Ал, линзаның сфералық бетінің жарық шоғын жинау немесе шашырату сияқты тамаша қасиеті ол тағыда жарықтың сыну құбылысының салдары ғана екенін ескертеміз.
Линза өте қарапайым оптикалық аспап, соған соншалықты талдау жасау қажет пе еді деген ой да тууы мүмкін. Бұл орайда айтарымыз әңгіме түсініктің түбіріне үңілуде екенін, көбінде оқушылар физикалық құбылыстың түпкі - түйінін түсінбей «күрделі» есептеулерді жүргізумен «әуестеніп» кетеді немесе біз оларды солай қарай «сүйреп» кетеміз. Сондықтан оқушылар линзалардың ғажап қасиеті, біріншіден, олардың жасалу заттарының тегіне байланысты екен деп есептейді. Екіншіден, линзалардың жарықты жинауы немесе шашыратуы өзінше ерекше құбылыс түрінде санайды. Сөйтіп, екі бірдей қате түсінікке ұшырайды. Мұны тікелей іс-жүзінде көріп жүрміз. Ал шынында, линзаның ғажап қасиетін жарықтың сыну заңы жасап беріп тұр. Сынғанда да жарықтың сфералық беттен сынуынан туыдаған көрініс.
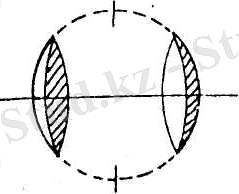 Сонымен линзалар дөңес және ойыс линзалар болып екі түрге бөлінеді, жеке және біріккен түрінде алу жолдары 1 - суретте көрсетілген.
Сонымен линзалар дөңес және ойыс линзалар болып екі түрге бөлінеді, жеке және біріккен түрінде алу жолдары 1 - суретте көрсетілген.
1 - сурет.
Ал, дөңес линзаның өзі екі жақ беті де дөңес, яғни қос дөңес жене бір жағы ғана дөңес линзалар болып тағы екіге бөлінеді.
Дәл сол сияқты ойыс линзада қос ойыс және бір жағы ойыс линза болып екі түрге топталады (41 - сурет) .

Ал осы қос дөңес бір жағы дөңес екінші жағы жазық және дөңес - ойыс, болып келген, жинағыш дәл осы сияқты қос ойыс, ойыс - жазық және ойыс -дөңес пошымды шашыратқыш линзалардаң жұмыс принципі 41, а - суретте көрсетілген.

Қос дөңес линзаның екі бетінің сфералық бет екенін 42 - сурет арқылы өте айқын көрсетіп беруге болады. Кез келген қос дөңес линзаның екі сфералық центрі бар. Және центрлер линзалардың өздеріне қарама - қарсы
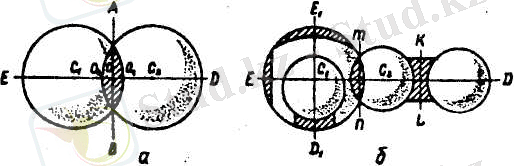
жақта әрі оның екі қисаю радиусы болады. Неғұрлым қос дөңес линза жұқа болса, онда оның центрлері линзадан солғұрлым қашық орналасады. Керісінше, қос дөңес линза неғұрлым қалың болса, солғұрлым оның центрлері линзаның өзіне жақын орналасады.
Қос дөңес линзаның екі центрін қосатын, яки басып өтетін түзуді осы линзаның оптикалық бас өсі деп аталады.
Ал егер дөңес линзаның екінші беті жазық болса, онда осы линзаның жазық жақ бетінің центрі шексіздікке барып орналасады. Яки линзаның тегіс бетінің центрі шектен тыс қашықтықта болады да, ал оның қисаю радиусы шексіз үлкен болып шығады. Әйтеуір бір оның да центрі бар деп есептеледі.
Енді линзаның бітім - пішініне зер салып қаралық. Дөңес және ойыс пошымды линзалар тым қалың немесе өте жұқа болуы мүмкін. Оның да тікелей іс - жүзілік маңызы бар.
Линзалардың сыртқы сипатына қарап, олардың жинайтынын немесе шашырататынын бірден аңғаруға болады. Дәл «бел ортасы» жіңішке линза өзіне түскен сәулені шашыратады. Ал, дәл бел ортасы жуан линзалар өзіне түскен сәулелерді «жұтады», жинайды. Қысқасы, «қарны» қампиғандары өзіне түскен сәулені «қарнына», өзіне жинай береді неғұрлым линза жуан болса, солғұрлым көбірек, «күштірек» жинайды.
«Белі» жіптіктей жіңішке линзалар өзіне түскен сәулелерді шашыратады. Қысқаша айтқанда линзаның ішкі «күш-қуаты», «іскерлігі» сыйқыр-сыры оның сыртқы сипатынан ап-айқын байқалады. (Мүмкін бұл да линзалардың мөлдірлігінің нақты дәлелі болар) .
Шынында да өте қалың линзаның центрінен оның жоғары және төмен ұштарына қарай сфералық бетінің майысуы соншалықты «өте тез өтеді» де линзаның бас өсіне перпендикуляр түзу бағытында, яғни линзаның ұзына бойындағы бағытта қалыңдықтың өзгеру «жылдамдығы» (градиент) өте тез өтеді. Басқаша айтқанда өзара өте тақау болып келіп түскен екі параллель сәулелердің лизадан өткендегі жол айырымы өте үлкен болады. Ал, линза өте жұқа болса, бұл айтылған беттің «майысуы» да, параллель өзара қатар сәулелердің жол айырымы да онша білінбейді.
Линза неғұрлым қалың болса, солғұрлым оның бетінің иілу центрі линзаға өте жақын және иілу радиусы өте қысқа болады. Ал линза неғұрлым жұқа болса, солғұрлым линзаның сфералық бетінің иілу центрі одан солғұрлым қашық болады, иілу радиусы да ұзын болады. Сонымен қатар линзаның өзінің де центрі бар. Ол нүкте линзаның бас өсі мен линзаның өз өсінің бойында жатады. Линзаның бұл өз центрі оның өз өсімен бас О 1 О 2 өстің қиылысқан О нүстесі болып есептеледі. Бұл О нүктесі линзаның оптикалық центрі деп аталады. Сөйтіп линзаның оптикалық бас өсінің бойында оның өзінің оптикалық центрі және осы оптикалық центріне симметриялы болып орналасқан екі сфералық центрлері жатады екен. Мысалы 43 - суретте линзаның екі С 1 және С 2 центрлері оның бас өсі О 1 О 2 түзуінің бойында жатыр.
Линзаның оптикалық центрі арқылы өткен кез келген түзу оның оптикалық өсі деп аталады. Кейде оларды «қосымша өстер» деп те атайды. Жалпы алғанда линзаның толып жатқан оптикалык, қосымша өстері және бір оптикалық бас өсі болады. Мысалы суреттегі О 3 О 4 өсі линзаның осындай өсі болып саналады.
Линзаның оптикалық бас өсіне параллель әрі өзара да параллель түскен сәулелер сол линзаның бас өсінің бойындағы бір нүктеге жиналады. Бұл нүктені линзаның фокусы деп атайды. Кейде оны линзаның бас өсінде жатқандықтан линзаның бас фокусы деп атайды. Ал, линзаның центрінен оның фокусына дейінгі қашықтықты линзаның фокус аралығы деп атайды. Оны суретте көрсетілгендей f деп белгілеп қабылданған.
Линзаның бас фокусының анықтамасын беру үшін біз жарық шоғын оның бас өсіне параллель етіп түсірдік. Ал шынында да линзаға кез келген бағытта түскен бірақ өзара параллель сәулелер де линзадан өтіп бір нүктеде жиналады. Олай болса, бұл нүкте де линзаның фокусы болуы тиіс Бірақ бұл нүкте линзаның бас фокусының бойында жатпайды. Сондықтан оны линзаның қосымша фокусы деп атайды.
Линзаның бас фокусын және қалған жәй фокустарын қамтитын бас өске перпендикуляр жазықтық жүргізсек, онда біз оптикалық үлкен маңызы бар жазықтық алған болар едік. Бұл ФЖ жазықтықты фокустық жазықтық деп атайды. (Бұрын бұл жазықтықты фокальдық жазықтық деп айтатын еді. Ал фокальді деген сөздің мағынасы фокустық нүктелер жататын жазықтық деген ұғым береді) . Линзаның екі фокусы болатыны сияқты, екі фокустық жазықтығы да болады. Яғни алдыңғы және артқы фокус жазықтығы бар.
Дау жоқ, линзаның өзіне түскен параллель сәулелерді жинау «қасиеті» ол аса айғақтап айтып жатқанымыздай оның сыртқы пішінінің сфералық бет түзеуінен туатыны рас. Және линзаны кәдімгі әйнектен де немесе басқа да мөлдір заттардан жасауға болады. Мысалы кейбір арнайы мақсаттағы линзаларды кварцтан, астұзының шөгіндісінен де жасауға болады. Әрине түптеп келгенде линзаның пішіні сфералық беттен басқа болуы да мүмкін. Айталық цилиндр немесе параболалық пішінді линзалар да жасалады. Бірақ ондай линзалар өте сирек қолданылады.
Линзаның құдіреті оның сырт пішініне қатысты болғанымен, таза мақсатта қолданылатын линзаларды арнайы дайындаудан өткізеді.
Мұндай оптикалық мақсатта қолданылатын әйнекті оптикалық әйнек деп атайды. Оптикалық әйнек өте біртекті болуы шарт. Оның үстіне бұл әйнек механикалық жағынан өте төзімді, химиялық әсерге мейлінше берілмейтіндей болуы қажет.
Жалпы алғанда оптикалық әйнектің құрамы негізінен кремнезом (Si O 2 ) болады да, оған белгілі мөлшерде натрийдің, калийдің, кальцийдің, барийдің, алюминийдің, бордың, қорғасынның т. б. тотықтары қосылады. Міне осы қоспалардың мөлшерінің ара салмақтарына байланысты әйнектің оптикалық қасиеті өзгереді.
Оптикалық әйнекті өңдеу, оларға қажет пішім беру өте үлкен шеберлікпен және асқан дәлдікпен іске асуы керек. Мысалы оптикалық бөлшектерді жасаудың шегі 1, 2мм болуы шарт. Қысқасы оптикалық бөлшектерді дайындаудың дәлдігі механикалық аса үлкен дәлдікті керек ететін бөлшектерді жасау дәлдігінен 500 есе артық болуы керек. Мұндай оптикалық әйнекті өңдеуде шектен тыс үлкен дәлдікті орындап беретін де оптикалық құбылыстың өзі. Ол интерференция құбылысы. Сөйтіп, оптикалық бір құбылыс екінші бір оптикалық үрдістің өтуіне тікелей көмегін тигізеді.
Ендігі тоқталып өтетін және оқушыларды ойландыратын мәселенің бірі - ол жинағыш, шашыратқыш линзалардың қасиетін сипаттағанда, олардың фокусын анықтағанда тек параллель сәулелерді пайдалану арқылы іске асырғанымызды баса көрсетеміз. Қысқасы біз линзаның физикалық қасиетін беруде негізінен параллель сәулелерді қарастырдық. Өйткені өмірімізде, табиғи жағдайда параллель сәулелермен істес боламыз. Шынында біз табиғи жағдайда Күннің сәулесін, тағы басқа аса үлкен жарық көздерін пайдаланамыз. Ал, өте алыс орналасқан жарық көздерінен келетін сәулелер негізінен өзара параллель болады. Тіпті жасанды жарық көздерін белгілі бір қашықтыққа орналастырып, одан шыққан сәулелерді өзара параллель болатындай күйге жеткізуге болады. Сондықтан линзалардың қасиетін зерттеуде параллель сәулелерді пайдаланамыз.
2. 1. Оптикалық құрал - лупа.
Лупа жеке бір немесе бірнеше линзадан тұратын линза жиынтығы. Олай болса, лупаны линза деп қараудан гөрі оны оптикалық аспаптар қатарына жатқызу дұрысырақ. Қысқасы, лупа жеке линзадан тұратын немесе линзалар жиынынан құралатын оптикалық ең қарапайым аспап.
Әрине, лупа ретінде алынатын линзаның өз ерекшелігі бар. Мұндай міндет атқаратын линзалар фокус аралығы өте қысқа болуы басты шарт.
Лупаны пайдаланғанда ол арқылы бақылануға тиіс затты лупаның алдыңғы фокусында өте тақау жататындай етіп орналастырады. Дәлірек айтқанда бақыланатын затты лупаның тура алдыңғы фокусына немесе фокус пен лупаның арасына, бірақ 55-суретте көрсетілгендей фокусқа өте жақын орналастыру қажет. Қалыптасқан ғылыми түсінік пен терминдік пен терминдік дәстүрге сәйкес бақыланатын нәрсенің орналасу орнын анықтағанда линзаның (лупаның) тікелей өзіне қатысты есептейді. Сондықтан бақыланатын нәрсенің линзадан қандай ара қашықтықта екенін көрсетуіміз керек. Бұд аралықты «а»-ға тең деп есептелік. Әрі бұл аралықты солай етіп таңдай білуіміз керек, осы нүктедегі нәрсенің кескіні, біріншіден, бар мүмкіндігінше үлкейтілген. Екіншіден, пайда болған кескін лупаға қараған бақылаушыдан адамның ең жақсы көру (25см) қашықтығында орналасып шығатындай болуы міндет.
Біз лупа арқылы бақылағанда нәрсені лупа мен оның фокус аралығына орналастыратынымызды айттық. Ал, нәрсе линза мен оның фокус аралығында орналасатын болса, онда оның кескіні жалған кескін болатыны мәлім. Әрі бұл кескін тура кескін екені де белгілі. Кез келген оптикалық аспаптың міндеті ол нәрсені үлкейтіп, әрі айқын көрсету. Олай болса, лупа да бұл міндетті ойдағыдай орындап береді. Сонымен лупа әрі үлкейтілген, әрі жалған, әрі тура кескін шығарып беретін аспап болды. Кез келген нәрсені жалпы көру, бақылау ол «көру бұрышына», оның шамасына байланысты. Қысқасы бақыланатын затты өте жақсы (айқын, нақты) көру үшін нәрсенің көзден қашықтығы 25см мөлшерінде ғана болмауы керек екен, сонымен қатар біз ол затты қандай көру бұрышымен көре алатынымыздың маңызы өте үлкен.
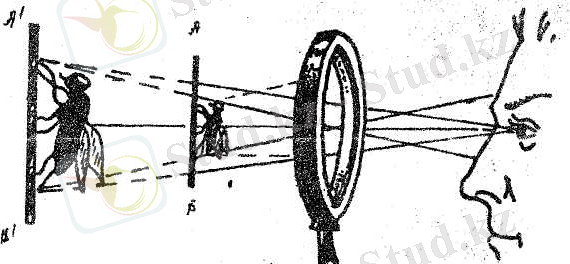
Әрине кез келген оптикалық аспаптар тәрізді лупаның да үлкейту шегі бар. Әрі ол үлкейту шегі пайда болған кескіннің нәрсенің өзінен қанша үлкен болып шығуымен аңықталады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz