Энергия сақталуының заңдары

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:

ТАҚЫРЫБЫ:

ТЕКСЕРГЕН: ТҰРЫСБЕКОВА Б. Ш.

ОРЫНДАҒАН: КАЛИЕВА Ұ.

ТОБЫ: ТФ-107

Мазмұны

КІРІСПЕ . . . 3

1 ЭНЕРГИЯНЫҢ ТҮРЛЕРІ . . . 4

1. 1 Кинетикалық энергия . . . 4

1. 2 Консерватив және консерватив емес күштер . . . 6

1. 3 Потенциалдық энергия . . . 9

2 ЭНЕРГИЯНЫҢ САҚТАЛУ ЗАҢЫ . . . 14

2. 1 Термодинамиканың бірінші бастамасы . . . 15

ҚОРЫТЫНДЫ . . . 21

ҚОСЫМШАЛАР . . . 22ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР . . . 28

Кiрiспе

Механика дегенiмiз - материя қозғалысының ең жай формуласы туралы iлiм, яғни денелердiң немесе олардың жеке бөліктерінің бiр-бiрiмен салыстырғанда орын ауыстыруы жайындағы iлiм.

ХIХ ғасырдың басында бу машиналарының қолданылуы жылуды механикалық жұмысқа неғұрлым тиiмдi жолмен айналдыру мәселесін шешудi өажет етті. Бұл мәселені тек техника тұрғысынан бiр жақты қарап шешу мүмкін емес едi. 1824 жылы француз инженерi Сади Карно жылудың жұмысқа айналуы жайындағы проблеманы жалпы түрде қарастырғаннан соң ғана бу машиналарының пайдалы әсер коэффицентiң шынымен-ақ арттыруга болатын болды. Сонымен қабат Карноның еңбегi энергияның берiлуi мен түрленуi туралы жалпы iлiмнiң шығуына негiз болды, ол iлiм кейiн термодинамика деп аталды.

Техника мен физиканың даму процестерiнде бiр-бiрiне тигiзетiн ықпалы жайындағы мысалдар ете көп. Техниканы негiзiнен езгерте алатын, осы күнгі маңызы өте зор проблемаларды, мысалы күн энергиясын тiкелей iс жүзiнде пайдалану немесе термоядролық реакция есебiнен атомдық ішкi энергияны шығарып алу проблемаларын шешу үшiн физикалық құбылыстарды одан әрi зерттеу керек болады.

Бiз өзiмiздi айнала қоршаған табиғатга қалайда болса бiр күш арқылы (серпiмдiлiк күштерi, тартылыс күштерi, үйкелiс күштерi, т. т. арқылы) бiрiне-бiрі әсер етуші денелердi кездестiрiп отырамыз. Сондықтан осындай жағдайларда денелер тек күштердiң ықпалымен ғана орын ауыстырады. Осылай болған соң, күштердiң денелердiң орын ауыстыруымен байланысты әсерiне сипаттама беру қажет болып табылады. Механикада осындай сипаттама ретінде бiр шама алынады. Сонда куштiң орын ауыстыру бойымен бағытталған қараушысы неғұрлым көп болса, куш түскен неғұрлым алысырақ жылжыса, ол шама соғұрлым үлкен болады. Осы шама жұмыс деп аталады.

1 Энергияның түрлері

1. 1 Кинетикалық энергия

Қорытқы күш әрекет еткен материялық нүкте қозғалысы

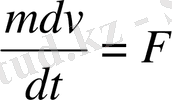(1. 1. 1)

теңдеумен өрнектеледі. Осы теңдеудің оң және сол жақтарын материялық нүктенің элементар орын ауыстыруы dS-ке скалярлы көбейтейік:

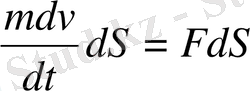
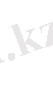Бұдан dS/dt=v екенін ескере отырып,

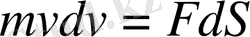
табамыз. Соңғы өрнектің оң және сол жағын нүкте траекториясының 1-орнынан 2-орынға дейiн интегралдап

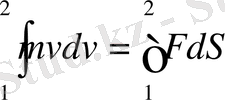
мынадай нәтижеге келеміз:

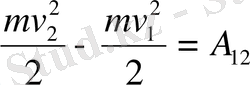(1. 1. 2)

Алынған нәтижеге қарағанда, материялық нүктеге әсер еткен барлық куштердiң қорытқы күші жасайтын жұмыс шаманың өзгеруіне тең. Бұл шама нүктенің тек бастапқы және соңғы жагдайына тәуелдә екені айқын, сондықтан күй функциясы болып тұрып, нүктеге (жүйеге) әрекет еткен қорытқы күштіің жұмыс істеу қабілетін анықтайды, яғни, кейiн көрсетілетіндей, қозғалыстың универсал қасиетін сипаттайды. Сонымен,

mv ² /2 физикалық шама қозғалыс энергиясын, яғни материялық нүктенің кинетикалық энергиясын өрнектейді:

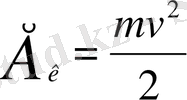(1. 1. 3)

Осыған байланысты (1. 1. 3) теңдігін

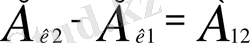(1. 1. 4)

Түрінде қайта жазуға болады. Алынған нәтижені материялық нүктелердің кез-келген жүйесі үшін жалпылау қиынға түспейді.

Саны N материялық нүктелерден тұратын жүйені қарастырайық. Жүйенің әрбір нүктесіне ішкі жіне сыртқы күштер әрекет жасайды. Жеке дара нүктенің қозғалысы қарастырылса, iшкi күштер оған қарағанда сыртқы саналып, жүйені құраушы әр нүктенің қозғалысы (1. 1. 4) теңдеуге бағынады. Жүйенің кинетикалық энергиясы деп жүйені құраушы материялық нүктелердің немесе сол жүйені ойша бөлген белшектерiнiғ кинетикалық энергияларының косындысын айтады. Ендi (1. 1. 4) теңдеуді жүйенің әрбір материялық нүктесіне немесе бөлiгiне ойша жазып, оларды бiр-бiрiне мүшелеп қосайық. Бұл амалдың нәтижесінде қайтадан кайтадан (1. 1. 4) -теңдеуін аламыз, тек алынған өрнек жеке нүкте үшiн емес, тұтас жүйе үшiн жазылған болады.

(1. 1. 4) -теңдеулерiн қосқанда, материялық нүктелер жүйесінде iшкi күштер жасайтын жұмыстың нольге тең еместiгiне көңіл аудару керек, яғни кинетикалық энергияның өсiмi тек сыртқы күштер жұмысына емес, сонымен катар iшкi күштер жұмысына да тәуелдi.

Өзінің мағынасына қарай (1. 1. 4) қатыс сыртқы күштер өрәсәнде орналасқан өзара әрекеттесетін материялық нүктелер жүйесі үшін механикалық энергияның сақталу зағын өрнектейді. Аса маңыздылығына орай бұл теңдеуді кинетикалық энергия теоремасы деп те атайды. Энергияның сақталу заңына терең талдау жасау үшін, яғни механикалық энергияның сақталу шарттарын нақтылау үшін, консерватив және консерватив емес күштер , потенциалдық энергия сияқты жаңа түсініктерді өарастыруға тура келедi. [2]

1. 2 Консерватив жене консерватив емес куштер

Күштерді олардың қасиетіне сәйкес консерватив және консерватив емес деп аталатын 2 топқа бөлуге болады. Осыған байланысты төмендегідей мысалдар келтiрейiк.

1. Материялық нүкте 1-орыннан 2- орынға екi түрлi S ₁₂ жене S ₁₃ жолдармен ауысқанда F _а = mg ауырлық күшінің iстейтiн жұмысын есептейiк. Жұмыс анықтамасы бойынша

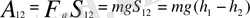(1. 2. 1)

Ал S ₁₃ жольиндағы жұмысты қосынды түрінде жазуға болады:

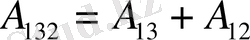
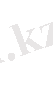(1. 2. 2)

Мұнда

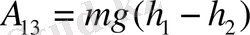
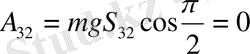
Соңғы мәндерді (1. 2. 2) тендiкке қойып, (1. 2. 1) -тi ескерсек,

екенін көреміз. Алынған нәтиже ауырлық күшінің кез-келген жолда iстейтiн жұмысы үшін дұрыс болатыны айқын. Бұдан ауырлық күші жұмысының мөлшері жолдың пішініне тәуелді емес, тек материялық нүктенің бастапқы және кейінгі орындарымен анықталатыны туралы өорытынды туады.

2. Ендi материялық нүктенің центрлiк күштер өрісіндегі қозғалысы кезiндегi жасалатын жұмысты есептейік. Мұндай өріс материялық нүктеге кеңістіктің кез-келген нүктесінде әрекет еткен күштің үнемі қозғалмайтын центр аркылы өтiп отыруы және оның шамасы тек сол центрге өашыөтыөөа тәуелді болуы сияқты екi қасиетпен ерекше сипатталады. Осындай өрістерге Күннің планеталарға әрекет ететін гравитациялық тартылыс күші немесе 2 нүктелік зарфдтар арасындағы электростатикалық әрекет күші мысал бола алады. Жалпы түрде центрлiк күштердің жасайтын жұмысы

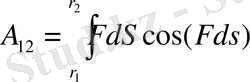
(1. 2. 3)
интегралымен анықталады, мұнда r ₁ және r ₂ материялық нүктенің бастапқы және соңғы орнын белгiлейтiн радиус-векторлар, dS - нүктенің элементар орын ауыстыруы, Ғ-центрлiк күш (1. 2. 1-сурет) . Сұлбаға қарағанда dscos(FdS) dr сондықтан

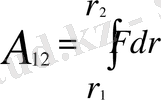
(1. 2. 4)
Бұдан центрлiк күш жұмысының шамасы нүкте жолының пішініне емес, тек оның бастапқы және соңғы орындарына, яғни r ₁ мен r ₂ мәндеріне тәуелділігі туралы қорытынды шығады.

Қарастырылған мысалдың маңызды салдары бар: егер өзара әрекеттескен материялық нүктелер бiр-бiрiне салыстырмалы қозғалмайтын болса, олардың кез-келген біріккен қозғалысында (1. 2. 3) -формуладағы интеграл үнемі нольге тең болады. Бұның өзi абсолют қатты денелерде әрекет жасаған iшкi күштердiң жұмысы сол денелердiң кез-келген қозғалыстарында нольге тен деген сөз.

Өзара әрекеттескен екi материялық нүкте үшiн жасалған қорытындыны центрлiк күштер арқылы әрекеттескен нүктелердің кез-келген жүйесi үшін де қолдануға болады. Себебi құраушы материялық нүктелердің орындары берiлсе, сол координаталар олар кұрған жүйенiң де кеңiстiктегi орнын анықтайды. Сонымен, центрлiк күштер жұмысы жуйенiң бастапкы орнынан соңғы орнына ауысу тәсiлiне (жол пiшiнiне) емес, тек құраушы нүктелердің шекті орындарына тәуелді.

Қарастырылған мысалдар күштердiғ бiр тобын iрiктеп алуға мүмкiндiк бередi: егер өзара әрекет күштер тек жүйенi кұраушы нүктелердiң кеңiстiктегi орнына (координаталарына) ғана тәуелдi болып және осы өзара әрекет ететін күштердiң iстейтiн жұмысы жүйе кез-келген бастапқы орнынан екінші бір орынға ауысқанда жүрген жол пішініне байланысты және соңғы орындармен анықталса, оларды консерватив немесе кейде потенциалдық күштер деп атайды.

Күштердiң консервативтігінің математикалық критерийi ретiнде сол күштердің тұйық жол бойындағы жұмысын, яғни

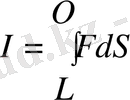(1. 2. 5)

интегралды есептеу нәтижесiн алуға болады.

Егер F күш консервативтi болса, материялық нүктенiң тұйық жолдың L ₁ және L ₂ бөліктеріндегі iстеген жұмыстары тең болуы керек (1. 2. 2 - сурет), яғни

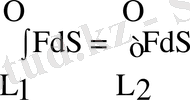
(1. 2. 6)
Интеграл шектерiн орын ауыстырғанда оның таңбасы кері өзгеретiндiктен, (1. 2. 6) қатысты былай жазайық:

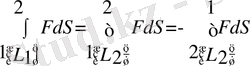
немесе

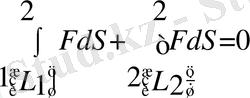
Алынған теңдiктi консерватив куштiң бастапқы (1) орыннан екiншi (2) орынға, ягни L ₁ жолы бойында, және (2) орыннан (1) орынға, яғни L ₂ қайта оралу жолында iстеген жұмыстарының қосындысы деп қарастыруға болады. Бұл теңдіктен математикалық мынадай нәтиже аламыз:

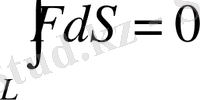
(1. 2. 7)
Яғни (1 . 2. 7) - қатыс әрі консерватив күштер күштердің (потенциалдық өрiс анықтамасы ретінде, әрі күштердің консервативтігінің критерийi ретiнде қарастырылуы мүмкін:

а) егер кез-келген тұйық траектория бойымен қозғалған нүктеге әрекет еткен күштің жұмысы нольге тең болса, ондай күш консервативті болады;

б) куш консервативтi болуы үшiн, оның кез-келген тұйық жолда iстеген жұмысы нольге тең болуы қажет және жеткілікті.

Сонымен қатар консервативті емес күштер қатарына гироскоптық күштер жатады. Бұл күштер материялық нүкте жылдамдығына тәуелді бола тұрып, үнемі жылдамдық бағытына перпендикуляр әрекет жасайды. Сондықтан материялық нүктенің кез-келген қозғалысы барысында, оның iшiнде тұйық траекториямен қозғалғанда да гироскоптьқ күштiң iстеген жұмысы нольге тең. Физикада бiрден-бiр белгiлi гироскоптық күш Лоренц күшi, яғни зарядталған бөлшекке магнит өрiсi тарапынан әрекет ететiн күш.

Консервативтi бола алмайтын барльқ басқа күштер консервативтi емес деп аталады. Мысалы, оларға сырңанау үйкелiс күштерi немесе газ ортада қозғалған денеге әрекет жасайтын кедергi күштерi сияқты диссипативтiк күштер жатады. Бұл күштер тек дененiң орнына ғана емес, сонымен қатар салыстырмалы жылдамдықтарға да тәуелдi. Мысалы, тұйық жүйелердегі кез-келген қозғалыс кезiнде диссипативтiк күштердiң жұмысы үнемi терiс таңбалы болады. [2]

1. 3 Потенциалдық энергия

Егер жүйеге тек консерватив жене гироскоптық күштер әрекет жасаса, өзара әрекет энергиясы ретiнде потенциалдьқ энергия түсiнiгiн қарастыруға болады. Мысал ретiнде дене мен Жерден тұратын қарапайым жүйені алайық. Дене Жер бетiнен онша алыс емес қашықтықта орналассын. Мұндай жағдайда Жер өрiсi бiртектi, ал әрекет күшi тұрақты деп санауға болады. Сонымен, дененi құраушы әрбiр материялық нүктеге шамалары тең ауырлық күштері әсер етедi. Энергияның жоғарыда келтiрiлген анықтамасына сәйкес потенциалдық энергия түсiнiгiн өарастыруғы енгізу үшiн жүйе бiр орыннан екiншi орынға ауысқанда оның құраушы нүктелерiне әрекет жасайтын күштердің жұмысын есептеу керек. Бiрiншi жағдайда дене Жер бетiнен h ₁ қашықтықта, екiншi жагдайда h ₂ қашықтықта, ал дене 1-орыннан 2-орынға ауысты деп санап, дене қозғалысын тудырған әрекет күштің жұмысын (1. 3. 1) формуламен есептейiк:

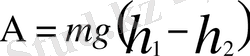(1. 3. 1)
Бұл теңдікке қарағанда mgh фиэикалық шама күй функциясы ретiнде жүйеге тускен куштің жұмыс iстеу қабiлетiн анықтайды және кейiн көрсетiлетiндей қозғалыстың универсал өлшемi болады. Сонымен, mgh шаманы консерватив ауырлық күш арқылы әрекеттескен екi дене жүйесiнiң энергиясын анықтау негiэi деп өарастырамыз. Жоғарыда айтылғандай, консерватив күштер жұмысы жүйе құраушы денелердiң тек бастапқы және соңғы күйлерiне, яғни денелердiң координаталарына ғана тәуелдi. Бұдан жүйе денелердiң күй функциясы болатын потенциалдық энергия тек жүйенi кұраушы нүктелердің координаталарына тәуелдi деген корытынды туады. Денелер жүйесiнiң потенциалдық энергиясын анықтау үшiн шартгы түрде энергиясы нольге тең жүйе күйiн таңдап алу керек. Осыған байланысты потенциалдық энергияны жүйенің энергиясы нольге тең күйге ауысқан кездегi консерватив күштер жасайтын жұмыс арқылы өрнектеуге мүмкiндiк туады. Қарастырып отырған мысалда энергиясы нольге тең күй үшiн кез-келген жағдайды алуға болады: 1, 2 нүктелер немесе Жер бетi. Нольдiк күй үшiн, мысалы, нүктенiң Жер бетiндегi жағдайын алайық. Онда потенциалдық энергия бiрiншi mgh ₁ шамасымен анықталып, екiншi куйде mg(h ₁ -h ₂ ) - ге тең. Сонымен потенциалдық энергия жүйенiң бастапқы күйiн таңдап алуға тәуелдi екенiн, яғни тұрақтыға дәлдiкпен есептелiнетiнi айқын болып отыр. Қарастырып отырған мысалда консерватив тартылыс күшi арқылы әрекеттескен дене мен Жерден кұрылған жүйенiң потенциалдық энергиясы

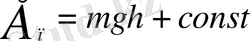
формуласымен анықталады, мұнда const -дененiң нольдiк деңгейдегi потенциалдық энергиясы.

Егер дене Жер бетiнен айтарлықтай, мысалы, Жердiң радиусымен салыстыратындай қашықтықта болса, Жердiң гравитациялық өрiсiн бiртектi деп санауға болмайды. Дегенмен, материялық нүкте және Жер жүйесi потенциалдық болатын центрлiк гравитациялық күштер өрiсiнен орналасып тұр. Олай болса, мұндай жүйеге де потенциалдық энергия түсiнiгiн қолдануға болады. Тек бұл есепте нольдiк күй үшiн жүйе құраушы денелердiң өзара әрекетiн ескермейтiндей алыс қашықтықта орналасқан жағдайын алу қолайлы. Потенциалдық энергияны есептеу барысында Жер козғалмайды, ал материялық нүкте оның гравитациялық өрiсiне қайсыбір бiрiншi күйден шексiз алыстаған нольдiк күйге орын ауыстырады деп санаймыз (1. 3. 1-сурет) . Осы тұрғыдан карағанда материялық нүктеге әрекет еткен күш жұмысы нүкте мен Жер жүйесiнiң бiрiншi жағдайдағы потенциалдық энергиясын анықтайды:

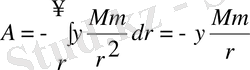
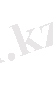
Яғни

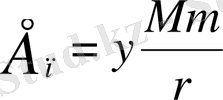
Тағы бiр мысал қарастырайық: созылған серiппенiң потенциалдық

энергиясын есептейiк. Серiппенi созғанда немесе қысқанда пайда болатын серпiмдiлiк күштерi центрлiк күштер катарына жатады. Сондықтан олар консерватив болады, яғни, серпiмдiлiк күштерi әрекет еткен жүйеде потенциалдық энергия түсiнiгiн енгiзуге мүмкiндiк бар.

Серiппенiң созылуын х ден белгiлейiк, ягни x= l - l ₀ →серiппенiң деформацияланған (1) және деформацияланбаған (l ₀ ) ұзындықтарының айырымы. Серпiмдiлiк Ғ күш тек созылуға не қосылуға тәуелдi. Егер х қашықтық онша үлкен болмаса, F=kx теңдiгi орындалады. Серiппе деформацияланған күйден бастапқы деформацияланбаған күйге қайтып оралғанда Ғ күш

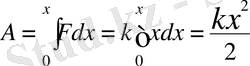
жұмыс жасайды.

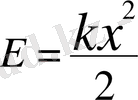Энергияның нольдiк деңгейi ретiнде шартты түрде деформацияланбаған серiппенiң энергиясын ала отырып, созылған немесе сығылған серiппенiң потенциалдық энергиясын табамыз:

(1. 3. 2)
Сонымен, қарастырылған мысалдар нәтижелерiн жалпылап, потенциялдық энергия шамасына түсiнiктеме берейiк. Құраушы материялық нүктелердің (бөлiктердiң немесе денелердiң) координаталары берiлген жүйенiң кез-келген бiр күйi (кеңiстiктегi орны) шартты түрде нольдiк күй (жағдай) деп қабылданады. Жүйе белгiлi бiр қарастырылып отырған күйден шартгы нольдiк күйге орын ауыстырғанда консерватив күштер жасайтын жұмыс жүйенiң қарастырылған жағдайдағы потенциалдық энергиясы болады. Консерватив күштер жұмысы жүйе орын ауыстырғандағы жол пiшiнiне тәуелдi емес, сондықтан нольдiк күй белгiленген болса, потенциалдық энергия шамасы тек жүйенi кұраушы материялық нүктелердiң қарастырылып отырған күйдегі координаталарымен анықталады. Дегенмен, соңғы сөйлемнен потенциялдық энергия шамасының жүйенiң бастапқы күйiне тәуелдi екенi байқалып тұр, яғни бастапқы жағдайды шартты түрде таңдап алуға байланысты потенциалдық энергияның сандық мәнi өзгередi. Мысалы, 1. 3. 2а-суреттегідей, бастапқы күй үшiн О΄ нүктенi таңдап алсақ, нүктедегi жүйенiң потенциалдық энергиясы, 1 нүктеден О нүктеге ауысқанда, консерватив күштер iстейтiн жұмысқа тең Е _п =А _1О , ал егер нольдiк күй үшін О΄ нүктенi таңдасақ, потенциалдық энергия Е ^΄ п=А _1О болады. Әрекет етушi күштер консервативтiк болғандықтан, 1- О΄ жолы бойындағы жұмыс 1-О- О΄ жолындағы жұмысқа тең : А=A _1O +A _OO немесе 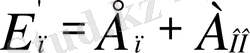. Мұндағы A _OO жұмыс мөлшері тұрақты, яғни жүйенің 1 нүктедегi координаталарына тәуелдi болмай, толығымен О және О΄ нольдiк күйлердi таңдау шарттарымен анықталады.

Сонымен, жүйенiң потенциалдық энергиясы бiрмәндi емес, тұрақтыға дейiн дәлдiкпен есептеледі. Бірақ бұл еркіндік физикалық корытындыларға ықпалын тигiэе алмайды, себебi физикалық құбылыстар үрдісі потенциалдық энергияның абсолют мәнiне емес, оның әр күйдегi мөлшерлерiнiң айырымыеа тәуелдi. Ал бұл айырым энергияның нольдiк деңгейiн таңдап алуға байланысты емес.

Ендi жүйе бiр күйден екiншi күйге өткенде консерватив күштер жұмысы потенциалдық энергияның кемуiне тең екенiн дәлелдейiк. Жүйе 1-нүктеден 2 нүктеге кез-келген жолмен орын ауыстырсын (1. 3. 2 б -сурет) . Консерватив күштердің осындай орын ауыстыруда жасаган А ₁₂ жұмысын 1 және 2 күйдегi жүйенiң Е _п1 және Е _п2 потенциалдық энергиялары арқылы өрнектеуге болады. Шынында, егер орын ауыстыру О нольдiк жағдай арқылы, яғни 1-О-2 жолмен жүргiзiлсе, онда А ₁₂ = А _1О2 =А _1О +А _О2 = А _1О -А _2О . Потенциалдық энергияның анықтамасы бойынша Е _п1 =А ₁₀ +const,

Е _п2 =А ₂₀ + const,

мұнда const- мәндерi бiрдей тұрақтылар. Олай болса

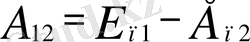
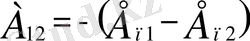
(1. 3. 3)

Сонымен, консерватив күштер жұмысы жүйенiң потенциалды энергиясының кемуiне тең. [2]

2 Энергияның сақталу заңы

Материялық нүктелердiң оңашаланған системасын алайық, ол

системада тек потенциялық күштер ғана әсер етедi дейiк. Системаның күйi оның конфигурациясымен және системаны түзетiн материялық нүктелердiң жылдамдықтарымен анықталады. Система бiр күйден екiншi күйге көшкенде системаны түзетiн материялық нүктелерге түсiрiлген күштер жұмыс iстейдi, оны бiз А _{1, 2} әрпiмен белгiлеймiз, сонда индекс 1-системаның бастапқы (1) күйiне, ал индекс 2 оның ақырғы (2) күйiне жатады. Бұл күйлердiң әрқайсысында материялық нүктелердiң жылдамдықтары мен олардың орналасулары әртүрлi, сондықтан система кинетикалық энергияның тиiстi Е _к1 және Е _к2 мәндерiмен және потенциялық энергияның лайықты Е _п1 және Е _п2 мәндерiмен сипатталады. Сонда А _{1, 2} жұмысын екi түрлi тәсiлмен өрнектеуге болады: не кинетикалық энергиялардың айырмасы арқылы

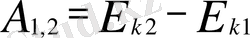
деп, не потенциялық энергиялардың айырмасы арқылы

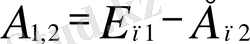
(2. 1)

деп, керсетсе де болады. Осы екi теңдiктi салыстырсақ, мына теңдеу шығады:

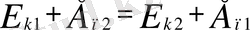
(2. 2)

Системаның кинетикалық және потенциялық энерияларының қосындысы оның толық механикалық энергиясы (Е) деп аталады:

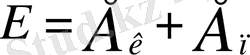
(2. 3)
Сонда (2. 2) теңдiктiң түрi мынадай болады:

(2. 4)
яғни өзiнде тек потенциялық күштер әсер ететiн оңашаланған системаның толық энергиясы тұрақты болып отырады. Осы қағида механикалық энергияның сақталу заңы деп аталады. Бұл механиканың негiзгi заңдарының маңызды салдарларының бірі болып табылады.

Бiр күйден екiншi күйге көшкенде, әрқайсысын жеке алғанда, кинетикалық энергия және потенциялық энергия өзгеруi мүмкін, бiрақ олардың қосындысы тұрақты болып отырады. Егер, мысалы, кинетикалық энергия ∆Е _к шамасына артса, онда дәл сондай шамаға потенциялық энергия кемуi керек. Бiрақ, есте болатын нәрсе сол системада әсер етушi күштер потенциялық күштер болса, тек сонда ғана оңашаланған система үшiн механикалық энергияның сақталу заңы орындалады. Потенциялық емес күштер (мысалы үйкеліс күштерi) бар болса, онда системаның кинетикалық және потенциялық энергияларының қосындысы тұрақты болып қалмайды. Энергияның сақталу заңын талдап қорытып кез-келген системаға қолдану туралы алда айтылады. [1]

2. 1 Термодинамиканың бiрiншi бастамасы

Берiлген жылу мөлшерi мен жұмыстың арасындағы эквиваленггiк механикалық энергияның сақталу заңын жалпылап топшылауға мүмкiндiк бередi. Алдында айтканымдай, системаның механикалық энергиясының өзгеруi ол системаға сырттан түсiрiлген күштер мен iшкi үйкелiс күштерi өндiрген жұмысқа пропорционал болады. Сонда бiз жылу әсерлерiн карастырмаған едiк. Жалпы жағдайды алғанда системаның энергиясы жұмыс өндiру нәтижесiнде ғана өзгермей, жылу берiлу есебiнен де, басқа да әсерлердің (мысалы жарықты сіңіру) есебiнен де өзгеруі мүмкiн.

Қандай да бiр системаны қарастырайық және оны бiр күйден екiншi күйге түсiретiн болайық. Мысалы: газдың белгiлi бiр мөлшерi сыртқы күштердің әсерiмен сығылуы мүмкiн және сонымен қатар ол газға қандай да бiр мөлшерде жылу беру нәтижесiнде оның қызуы да мүмкiн. Системаның әрбiр күйiн сипаттайтын белгiлi бiр шамаларды тағайындап алу арқылы ол күйдi макроскопиялық тұрғыдан анықтауға болады. Мұндай шамалар параметрлер деп аталады. Идеал газ үшiн оның күйiн аныктайтын V-көлем, P-қысым, T-температура үшеуінің кез-келген екеуi болады, өйткенi идеал газдың берiлген мөлшерiнiң күйiн бұл 3 шаманың кез-келген екеуi (мысалы: Р-қысым мен Т-температура) анықтайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.