Музыкалық шкала құрылғысы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Қазақстан Республикасының Оқу-ағарту министрлігі
Абай облысы

Бағыты:
Секциясы: Қолданбалы математика
Тақырыбы: Қарапайым гамма. Музыкалық шкала құрылғысы

Авторы: Токтарханова Айжан Дарыновна
11 Б сынып оқушысы
Таңжарықов Ақылжан Бақытжанұлы
11 А сынып оқушысы
Ыбырай Алтынсарин атындағы №37 гимназиясыКММ
Жетекшілері: Баймаганбет Жадыра Кошербаевна,
Сагатбекова Жанар Каликановна
математика пәнінің мұғалімдері
Ыбырай Алтынсарин атындағы №37 гимназиясыКММ

Семей - 2023
Мазмұны

1. Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...3
2. Негізгі бөлім
2.1. Музыкалық шкалаға жалпы шолу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.2. Музыкалық шкала бағынатын математикалық заңдылықтар ... ... ... ... ..
2.3.Арифметикалық, геометриялық прогрессия заңдылықтары арқылы құрылған жиілік тізбегі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
2.4. Диез, бемоль ұғымдары ... ... ... ... ... ... ... ... ...
3. Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
4. Қолданылған әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

Кіріспе
Жобаға негіз болып отырған қос сала - математика мен музыка. Екеуі де ертеден белгілі болған ғылымдар. Музыканың кей заңдылықтары тікелей математикаға бағынады. Оларда сан идеясы мен қатынас билік етеді.
Ресей және совет пианисті Г. Нейгауз: Музыка және өнер туралы, олардың арасындағы байланыс пен қарама-қайшылықтар жөнінде ойлана келіп, математика және музыка адам рухының қиыр полюстерінде орналасқан, адамның барлық рухани шығармашылық жұмысы осы екі антиподпен шектеліп, анықталады, сонымен қатар, ғылым және өнер саласында адамзаттың жасағанының барлығы осылардың арасында орналасады деген шешімге келдім, - деген. Яғни ғылым әлемінің шымылдығының бір қанаты математика болса, бір қанаты музыка дейді. Келісерлік пікір. Себебі математика ғылымдардың арасындағы ең абстрактілісі, ал музыка өнердің ең ерекшесі, тартымдысы, құлақтан кіріп, бойды алары. Екі сала өз бағытының үздігі болғасын да Генрих Густавовичтің пікірін толық қанағаттандыра алып тұр.
Математика мен музыканың байланысы үлкен нәтижеге, айтарлықтай оң өзгеріске апарарын ғалымдар тобы дәлелдеді. Кезекті зерттеудің қорытындысы бойынша математикалық тесттен музыкамен айналысатын оқушылар музыкамен айналыспайтын оқушыларға қарағанда анағұрлым жоғары ұпай жинаған. Ал Эрве Платель бастаған сегіз адамнан тұратын халықаралық ғалымдар тобының зерттеуіне сүйенсек, музыкант емес алты жас француздың музыка тыңдаған кезде мидың логикаға жауап беретін бөлігінің жақсы жұмыс атқарғанын дәлелдеді.
Айтылған деректердің дәм-тұзын кіргізе түсу үшін осы байланысты ары қарай зерттеп, дәйекті ойымызбен, ғылыми негіздердің көмегімен келтірген мысалдарымызбен бөліспекке бекіндік.

Қарапайым гамма. Музыкалық шкала құрылғысы
Музыкалық шкалаға жалпы шолу
Жалпы музыканың негізінде музыкалық тон немесе белгілі бір биіктіктегі дыбыс жатыр. Физикалық тұрғыдан алғанда, музыкалық тон - ауадағы белгілі бір тұрақты жиіліктегі тербелмелі процесс. Мысалы, ля тоны 440 герц (секундына) жиілігі бар процеске сәйкес келеді. Жалпы, біздің құлағымыз 16-дан 20000 герцке дейінгі кең жиілік диапазонындағы тондарды қабылдай алады, ал 4000 герцке дейінгі аймақта секундына бір ғана тербеліспен ерекшеленетін дыбыс биіктігін ажырата алады.

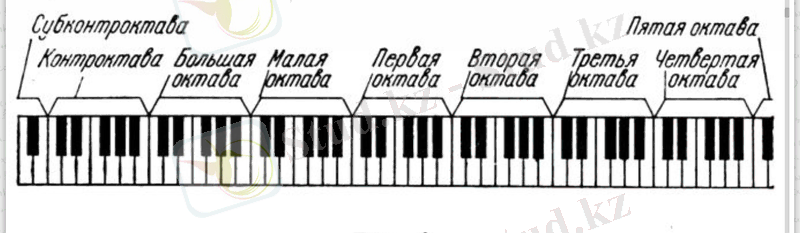
Дегенмен, музыка үшін тондардың көп түрі қолданылмайды. Фортепиано пернесінің суретін қарастырайық (1-сурет). Біз барлығы 90 ақ және қара кілттерді көреміз. Оларды басу арқылы біз тек 90 түрлі дыбысты - әртүрлі биіктіктегі тондарды шығара аламыз.
Ежелгі дәуірде Ежелгі Египеттің Фивия қаласына жақын жерде әр таң сайын бұл дыбысты Мемнон колоссы деп аталатын алып мүсін шығарып, фивандық музыканттар сол арқылы аспаптарын күйге келтірген деген аңыз бар. Мемнон Колоссы біздің дәуіріміздің басында дыбыс шығаруын тоқтатты және қазір аңыздың рас не жалған екеніне көз жеткізу мүмкін емес.
Бұл нақты қандай тондар? Мұнда фортепиано диапазонындағы ортаңғы, ең көп тараған бөлім - бірінші октаваға арналған жиіліктер кестесі берілген (2-сурет).
Тон
до1
ре1
ми1
фа1
соль1
ля1
си1
до2
Герцтегі жиілік
262
294
330
349
392
440
494
523

Бір қарағанда, бұл тондардың жиілігінен ешқандай ерекшелік байқалмайды. Оның өсуінен басқа, қандай да бір заңдылықты байқау қиын. Сонымен қатар, 440 санын қоспағанда, көрсетілген жиіліктердің қалған бөлігі нақты сандармен емес, иррационалдармен өрнектеледі;

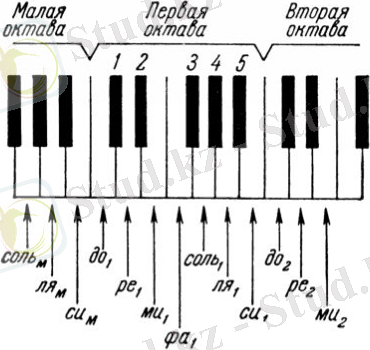
1 -- до диез = ре бемоль,
2 -- ре диез = ми бемоль,
3 -- фа диез = соль бемоль,
4 -- соль диез = ля бемоль,
5 -- ля диез = си бемоль.
Кестеде ең жақын бүтін санға дейін дөңгелектелген нұсқасы берілген. Сонымен, ми1 тонына сәйкес келетін жиілік 330 емес, 329-ға тең т.с.с.
Неліктен музыкалық шкала үшін дәл осы тондар таңдалған? Музыканың негізі ретінде қандай тондарды қою керек деген сұрақ ежелгі дәуірде пайда болды, бірақ соңғы шешім салыстырмалы түрде жақында, XVIII ғасырдың басында қабылданды. Кез келген биіктіктегі дыбыстарды барлық музыкалық аспаптарда еш кедергісіз қабылдау мүмкін болса, бұл сұрақ туындамас еді. Көптеген музыкалық аспаптарда - скрипкада, виолончельде - сіз кез келген тонды (аспаптың диапазонында) ала аласыз.
Мұндағы жағдай судың қату және қайнау нүктелері белгіленетін және алынған интервал 100 тең бөлікке бөлінген температура шкаласын салудағыдай қарапайым емес. Музыкада үндестіктер орасан зор рөл атқарады, яғни әр түрлі биіктіктегі бірнеше дыбыстардың бір мезгілде дыбысталуы айрықша маңызға ие. Бірақ дыбыстардың барлық комбинациялары үйлесімді емес. Сондықтан музыкалық шкалаға берілген дыбыспен бірге бір мезетте ең табиғи дыбыстарды енгізген жөн. Бұл ойлар әлі де біршама анық емес; бірақ нақты нені білдіретіні кейінірек белгілі болады.
Арфа (лира, кифара) сияқты аспаптар ертеде белгілі болған. Бұл аспаптардағы, сондай-ақ фортепианодағы дыбыстардың қайнар көздері ішектер болып табылады. Ежелгі уақытта біз қазір қосымшада сипаттайтынға ұқсас жолдармен эксперименттер болған болуы мүмкін. Біз дәл қазір тілге тиек еткелі отырған тәжірибе ежелде жасалған болуы да мүмкін. Фортепиано ішектерінде бастапқы күйде демпферлер - ішектердің дыбысталуына жол бермейтін киізбен жабыстырылған төсемдер орналасқан. Пернені басқан кезде демпфер алдымен тартылып, жіпті босатады, содан кейін балға жіпке соғылады. Егер пернені қалдырсаңыз, бос жол ұзақ уақыт бойы естіледі; кілт босатылса, демпфер жіпке түсіп, оның дыбысын тоқтатады. Егер сіз пернені баяу бассаңыз, демпфер жіпті босатады, бірақ балға соқпайды, біз оның дыбысын естімейміз. Енді келесі тәжірибені жасайық. Тиісті жолды дыбыссыз шығару үшін 440 герц жиілігінің тонусына сәйкес келетін пернені баяу басамыз. Содан кейін біз лям пернесін (кіші октава) басып, оны бірден босатамыз. Біз перне орнына оралғанда тоқтайтын лям пернесінің (220 герц) қысқа дыбысын естиміз. Нәтижесінде ля1 жолының дыбысын естиміз. Шығарылған ля1 үні дыбысталған лям үнін резонансқа байланысты өзі дыбыстай бастады. Бұл жолдың тербелісі бір қарағанда көрінгеннен гөрі күрделі процесс екенін көрсетеді. Негізгі жиілігі 220 герц болатын ішек те 440 герц жиілікте тербеледі, сонымен қатар ол резонанс арқылы осы жиілікпен бапталған ішекке әсер етеді. Бұл тәжірибені фортепианоның және басқа музыкалық аспаптардың әртүрлі ішектерінде қайталауға болады және нәтиже әрқашан бірдей болады: мәселен, f герц жиілігіндегі перне 2f герц жиіліктегіпернеге азды-көпті әсер ете алады.
Жоғарыда айтқанымыздай, музыкалық шкаланы оған кіретін тондар бір-бірімен "үндес" болатындай етіп құрған дұрыс. Қос жиіліктің тоны бастапқы жиіліктің тонымен максималды түрде үндес келеді (бұл дыбыс бүтін бірлік сияқты естіледі, тек арнайы эксперименттер оның дыбысынан қос жиіліктің тонын ажыратуға мүмкіндік береді).
Сондықтан келесі шартты енгізген жөн: музыкалық шкала f жиілігімен бірге 2f жиілігін қамтуы керек. Егер біз f-тен төмен жиіліктер туралы айтатын болсақ, онда бірінші кезекте шкаладағы f жиілігімен бірге f2 жиілігінің болуын қамтамасыз ету қажет. Берілген дыбыс пен қос жиілікті дыбыс арасындағы аралық октава деп аталады. Оның мағынасы өте кең; Дунаевскийдің "Отан туралы әндерін" мысалға алсақ: "Мәскеуден оның шетіне дейін" бөлімі октава интервалынан басталады. Музыка үшін тек октавалық интервалдар жеткіліксіз - әрі қарай біз оның негізгі тонына сәйкес келетін басқа тондарды табу үшін аспап пернелеріне жасалатын кезекті эксперименттерімізді жалғастырамыз. Бірақ алдымен музыкалық шкаланы құру кезінде ескерген жөн болатын тағы бір жалпы ойды қарастырайық. Бізге берілген әуенді түпнұсқаға қарағанда жоғары немесе төмен етіп ойнату мүмкіндігінің барын қарастыру қажет. Жалпыға ортақ мысал, бір әнді дауыстың сипатына байланысты әр түрлі, жоғары немесе төмен айтуға болады: тенор жоғары нотада, басс төменгі нотада айтуға ыңғайлы. Интервал интервалды құрайтын дыбыстардың жиіліктерінің қатынасымен сипатталады; көріп отырғанымыздай, "октава" интервалында бұл қатынас 2-ге тең. Әуенді жоғарыға жылжыту дегеніміз - оны басқа дыбыстармен, сәйкесінше жоғары дыбыстармен ойнату, бірақ әр интервалда тон жиіліктерінің қатынастарын дәл сақтау. Мысалы, егер біз түпнұсқада (ми -- до -- ми -- до -- фа -- ми -- ре), бірінші октавада "чижик" әуенін ойнайтын болсақ, онда біз қолданатын жиіліктер (герцте) келесідей:

330 -- 262 -- 330 -- 262 -- 349 -- 330 -- 294.

Егер біз бұл әуенді жоғарыдағы үш пернеге (си -- соль -- си -- соль -- до -- си -- ля) жоғарылататын болсақ, онда әуен бұрмаланбайды. Яғни жиілік көрсеткіші келесідей болады:

494 -- 392 -- 494 - 392 - 523 -- 494 -- 440.

Әуеннің әр интервалындағы жиілік қатынастарының сақталғанын тексеру қиын емес:

330262=494392, 349262=523392 т.с.с.

Егер біз интервалдарды түпнұсқадан өзгеше етіп қолдансақ, әуеннің бұрмаланғанын байқаймыз. Атап айтқанда, егер " чижикті " бір пернеге жоғары етіп өзгертсек, яғни фа -- ре -- фа -- рe -- соль -- фа -- ми, демек ол мынадай жиілікте болмақ:

349 - 294 - 349 - 294 - 392 - 349 - 330.

Осы орайда әуеннің сипаты анық бұрмаланған; оны жиілік қатынастарын есептеу арқылы білеміз:
330262 != 349294 т.с.с.

Шындығында, "чижикті" фа-дан бастауға болады, бірақ қара пернелерді пайдалануға тура келеді; бұл туралы төменде тарқатып айтамыз.
Енді біз екі шартты қанағаттандыратын тондардың шкаласын құрдық делік:
а) әр f тонымен бірге шкалада 2f және 12 f тондары бар
б) шкала әуендерді бұрмалаусыз жеткізуге мүмкіндік береді.
Бір октаваның ішінде шкаланың тондары келесідей болсын:
f = f0f1f2 ... fm-1fm = 2f.
Бұл дыбыстардың өзі қарапайым әуенді құрайды. Төменгі тон f0 -ден f1- ге көтерілуі үшін оны еш бұрмалаусыз жоғары көтерейік.
Жаңа әуен f1 дыбысынан басталып, f1 дыбысының октавалық қайталануы болып табылатын fm+1 дыбысымен аяқталады (fm= 2f0 болғандықтан). fm+1 дыбысы октаваның соңғы дыбысынан жоғары (f0, fm), бірақ біз оны fm-нен кейінгі бірінші дыбыс деп санаймыз. Шынында да, егер біздің шкалада fm мен fm+1 =2f1 арасында f' үні болса, онда сол шкалада 12 f' тоны болатын еді және fm f' fm+1 теңсіздігінен төмендегідей нәтиже шықпақ:
f012 f'f1
Бірақ, шарт бойынша, f1 f0-ден кейінгі бірінші дыбыс, сондықтан fm мен fm+1 арасында ешқандай да f' болмайды.
Бір сатыға ауысқаннан кейін, біздің әуеніміз f1 -ден бастап fm+1-ге дейінгі бірдей масштабтағы тондармен бейнеленуі мүмкін. Өйткені бастапқы әуен m+1 түрлі дыбыстардан тұрады, ал f1 - ден fm+1 - ге дейін біздің шкалада дәл m+ 1 түрлі тондар бар: f1 , f2, ..., fm, fm+1, жаңа әуеннің көрінісі мына нұсқада болмақ:

f1f2 ... fm fm+1.
Ол бастапқы әуенге сәйкес келетіндіктен, біз мынандай теңдіктерді аламыз:
f1f0 =f2f1, f2f1 =f3f2, ..., fmfm-1 =fm+1fm

немесе f1f0 =f2f1=...=fmfm-1 =fm+1fm (1)
f0, f1, f2... fm жиіліктері геометриялық прогрессияны құрайтынын байқадық. Енді осы прогрессияның еселігін табамыз және оны q арқылы белгілейміз де fm = qmfm = 2f0 өрнегі арқылы qm= 2 екенін анықтаймыз. Егер m саны (f0 мен 2f0 жиіліктерінің арасындағы қадам саны) белгілі болса, шкаланың өзі толығымен анықталады.
Әрі қарайғы зерттеуге ыңғайлы болуы үшін f0, f1 ... жиіліктерінен олардың екілік логарифміне lg2 f0, lg2 f1... өтейік. Октава (f0, 2f0) бұл процесте lg2 f0-ден lg2 2f0 = lg2 f0+1 жиілігіне дейінгі аралыққа өтеді, яғни ұзындық аралығы 1. Ал f0, f1,..., fm геометриялық прогрессиясы lg2m2 =1m айырмашылығы бар lg2 f0, lg2 f1,..., lg2 fm арифметикалық прогрессиясына өтеді. Осылайша, логарифмдер осінде біздің шкала А, А+ 1m, А + 2m, ..., А + 1 нүктелерінен тұрады, онда А арқылы біз lg2 f0 шамасын белгіледік.
т санын қалай таңдаймыз?
Біз оның тербелісі кезінде тағы қандай дыбыстық жиіліктер шығарылатынын білу үшін пернелерге жасайтын эксперименттерге қайта ораламыз. Үштік жиіліктің болуын тексерейік. Ол үшін біз 220 герц жиілігіне сәйкес келетін "ляm" (кіші октава) пернесін және 660 герц жиілігіне сәйкес келетін "ми2" (екінші октава) пернесін (бірінші октаваның ми1 тонына сәйкес келетін 330 герц жиілігінің октавалық қайталануы) қолданамыз. Жолды демпферден босатып, ми2 пернесін ақырын (дыбыссыз) басамыз. Содан кейін, бұрынғыдай, лямпернесін қатты басыңыз және оны босатыңыз; осыдан кейін біз босатылған ми2 жолының дыбысын естиміз. Сонымен, үштік жиілік перненің дыбысында да болады. Сіз тәжірибені әрі қарай жалғастыра аласыз және төртінші еселік тондардың дәйекті болуын анықтай аласыз, бірақ бұл таңқаларлық емес, өйткені 4f= 2-2f екені белгілі; әрі қарай - бесінші еселік және т.б.; бірақ келесі тондар, үшіншіден кейін, өте әлсіз көрінеді. Барлық 2f, 3f, 4f, ... тондары f негізгі тонының обертондары деп аталады; олардың бірлескен дыбысы фортепианода алынған дыбысты кернейде немесе скрипкада алынған дыбыстан ажыратуға мүмкіндік беретін ішектің дыбысына тән тембр береді. Әуен дыбысының сұлулығы обертондардың саны мен салыстырмалы мағынасына ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.