7-9 сыныптарда үшбұрыштардың ұқсастық пен теңдік белгілерінің қолданылуы


Мақала
Г. С. Заманбекова, Т. Т. Абдығали
Шәкәрім атындағы университеті КеАқ, Семей қаласы.
Мектеп геометриясындағы үшбұрыштардың ұқсастық және теңдік белгілерінің қолданысы.
Мақалада мектептегі геометрия курсындағы үшбұрыштар бөлімінің бағдарламасы айтылады. Кіріспе бөлімде геометрия курсына жалпылама сипаттама берілген. Негізгі бөлімде үшбұрышқа анықтама беріп, оның түрлері мен қасиеттеріне тоқталдық. Үшбұрыштың теңдік және ұқсастық белгілеріне арналған теоремаларға дәлелдемелер жүргіздік. Сонымен қатар, әр белгіге жеке тоқталып, әрқайсысына мысалдар келтірдік. Есептерді шығару барысында ұқсастық және теңдік белгілерін дұрыс қолдануды көрсеттік. Қорытынды бөлімде, келтірген мысалдардың қолданыстағы маңызы туралы айтылады. Қандай салаларда үшбұрыштың белгілері қолданылатыны жайлы сөз қозғалды.
Түйін сөздер : геометрия, үшбұрыш, теңдік белгі, ұқсастық, қолданыс.
- Кіріспе.
Геометрия- қоршаған ортаны зерттеуде, ой- өрісімізді, кеңістікте елестету дағдымызды дамытуда маңызы зор сала. Геометрия курсының бағыты- кеңістіктегі және жазықтықтағы фигуралар мен олардың қасиеттеріне талдау жасап, оларды мектеп оқушыларының бойына дарыту. Осы бағыт жүзеге асу үшін геометриялық фигураларды зерттеп, оның қасиеттеріне және ерекше белгілеріне мән берген дұрыс деп ойлаймыз.
Жалпы, геометрия курсы екі бөлімнен тұрады: планиметрия және стереометрия. Біздің мақаладағы тақырыбымыз 7-9 сыныптарына арналған планиметрия курсындағы тақырып.
Геометриялық фигуралардың ішінде үшбұрыштарды маңызды ұғымдардың қатарына жатқызамыз. Себебі, үшбұрыштарды күнделікті өмірдегі қолданыста да, архитектура саласында да, медицина салаларында қолданамыз. Үшбұрышты геометрия оқулықтарында көпбұрыштың дербес жағдайы ретінде қарастырады.
- Негізгі бөлім.
Үшбұрыш- ең қарапайым фигура. Бір түзудің бойында жатпайтын үш нүктені қосатын кесінділермен шектелген жазықтықтың бөлігі- үшбұрыш деп аталады. Оқушылар үшбұрыш- үш нүктеден, үш қабырғадан және үш бұрыштан ғана тұратын фигура екенін бастауыш сыныптардан біледі.
Үшбұрыштың теңдік белгілерін ажырата білу үшін, үшбұрыштың түрлерімен таныс болу міндетті. Бұл фигураның бес түрі бар:
- Теңқабырғалы үшбұрыш
- Теңбүйірлі үшбұрыш
- Тікбұрышты үшбұрыш
- Сүйірбұрышты үшбұрыш
- Доғалбұрышты үшбұрыш
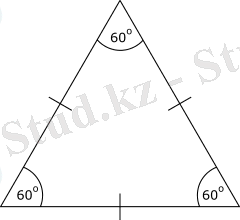
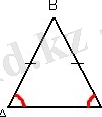
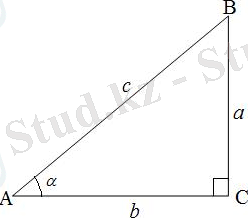
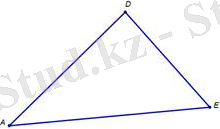
Үшбұрыштар геометрияның негізгі пішіндерінің бірі болып табылады. Олардың бірнеше қасиеттері бар, соның ішінде ұқсастық қасиетіне тоқталсақ. Ұқсас үшбұрыштар - сәйкес бұрыштары тең және сәйкес қабырғалары пропорционал үшбұрыштар. Осындай үшбұрыштардың мағынасын түсіну көптеген есептерді, мәселелерді шешу үшін өте маңызды дағды болып табылады. Осы білімнің арқасында біз үшбұрыштардың қабырғалары арасындағы пропорционалдық қатынастарды таба аламыз, сонымен қатар бұрыштардың мәндерін тани аламыз. Бұл өз кезегінде геометрия мен физикаға байланысты әртүрлі практикалық есептерді шешуге көмектеседі. Сондай-ақ, мұндай үшбұрыштардың мағынасын білу сәулет пен құрылыста - әртүрлі объектілердің пропорциялары мен өлшемдерін анықтауға көмектеседі. Сонымен қатар, үшбұрыштардың ұқсастығын түсіну пішінді бұзбай, олардың өлшемін үлкейтетін немесе азайта отырып, ұқсас фигураларды салуға мүмкіндік береді. Бұл графикалық дизайнда, модель жасауда және басқа да көптеген салаларда қолданбаларға ие.
Ұқсас үшбұрыштардың қасиеттері.
Ұқсас үшбұрыштар олардың ұқсастығын анықтауға және есептерді шешу үшін пайдалануға мүмкіндік беретін бірқатар негізгі қасиеттерге ие:
- Ұқсас үшбұрыштардың сәйкес бұрыштары тең.
- Ұқсас үшбұрыштардың сәйкес қабырғаларының ұзындықтары пропорционал.
- Ұқсас үшбұрыштардың қабырғаларының ұзындықтары мен биіктіктерінің қатынасы тең.
Осы қасиеттерді біле отырып, ұқсас үшбұрыштардағы белгісіз шамаларды табу үшін Пифагор теоремасын, қабырғалардың пропорционалдылық теоремасын және басқа да математикалық құралдарды қолдануға болады.
Үшбұрыштардың ұқсастығын білу және түсіну кеңістіктік объектілерді және олардың байланыстарын талдау қажет болатын әртүрлі салалардағы мәселелерді шешуге мүмкіндік береді. Мұндай үшбұрыштар белгісіз параметрлерді есептеуге және әртүрлі математикалық есептерді шешуге арналған қуатты құрал болып табылады.
Үшбұрыштың теңдік белгілері.
Теорема (I белгі) . Егер бір үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы сәйкесінше екінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелденуі: AB = , AC = болатындай ABC және үшбұрыштары берілген. Енді, екі үшбұрыштың теңдігін дәлелдейік.
болғандықтан, төбесі төбесімен, ал және қабырғалары сәйкес AB және AC сәулелерінде жататындай етіп, бұрышын CAB бұрышына беттестіруге болады. Берілген үшбұрышқа тең үшбұрыштың бар болатыны жөніндегі 8- аксиома бойынша мұндай үйлестіру мүмкін және бір ғана түрде анықталады. Ал AB = , AC = болғандықтан, қабырғасы AB қабырғасымен және қабырғасы AC қабырғасымен беттеседі. Олай болса, және ABC үшбұрыштары толық беттеседі. Онда бұл үшбұрыштар өзара тең. Теорема дәлелденді.
Теорема (II белгі) . Егер бір үшбұрыштың бір қабырғасы мен оған іргелес бұрыштары сәйкесінше екінші үшбұрыштың бір қабырғасы мен оған іргелес бұрыштарына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелденуі: AB = , және болатындай ABC және үшбұрыштары берілген. Енді, екі үшбұрыштың теңдігін дәлелдейік.
болғандықтан, төбесі төбесімен беттесетіндей етіп, қабырғасы AB сәулесінде жататындай етіп, AB түзуіне қатысты C және төбелері бір жарты жазықтықта жататындай етіп, үшбұрышын ABC үшбұрышымен беттестіреміз. AB = болғандықтан, төбесі төбесімен беттеседі. және болғандықтан, сәулесі AC сәулесімен, ал сәулесі BC сәулесімен беттеседі. Сонымен, ABC және үшбұрыштары толық беттеседі. Бұл теорема үшбұрыштардың бір қабырғасы мен оған іргелес екі бұрышы бойынша теңдік белгісі деп аталады.
Теорема (III белгі) . Егер бір үшбұрыштың үш қабырғасы сәйкесінше екінші екінші үшбұрыштың үш қабырғасына тең болса, онда мұндай үшбұрыштар тең болады.
Дәлелденуі: Бұны мына суреттен көре аламыз:
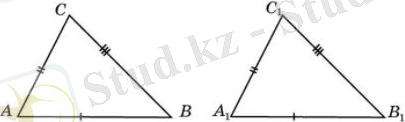
Екі үшбұрыш тең деп аталады, егер осы екі үшбұрыштың сәйкесінше қабырғалары және бұрыштары өзара тең болса. Тең үшбұрыш дегеніміз осы болады. ABC және үшбұрыштарында сәйкес қабырғалары- AB және , AC және , BC және тең. Сондықтан, осы үшбұрыштар теоремаға сәйкес тең болады. Бұл үшбұрыштардың бұрыштары да өзара тең болады.
Мектеп курсындағы геометрияда үшбұрыштарға байланысты есептер көп уақытты және аса қатты мұқияттылықты талап ететін есептер болып келеді. Осы тақырыпқа байланысты бірнеше практикалық есептерге мысал келтіретін болсақ:
1-мысал.
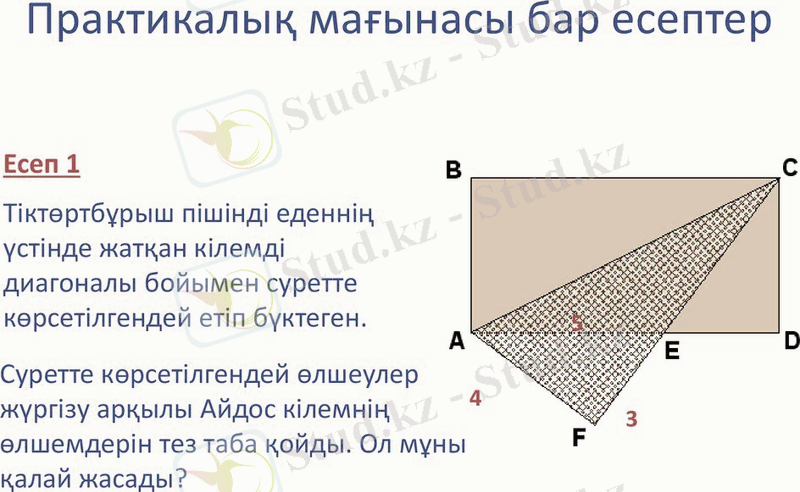
Тіктөртбұрыш пішінді еденнің үстінде жатқан кілемді диагоналы бойымен суретте көрсетілгендей етіп бүктеген. Суретте көрсетілгендей өлшеулер жүргізу арқылы Айдос кілемнің өлшемдерін тез таба қойды. Ол мұны қалай жасады? ∆ AFE және ∆ CDE теңдігін дәлелдеңдер.
Шешуі: ∆ AFE және ∆ CDE қарастырамыз.
- AF=CD (тіктөртбұрыш қабырғалары)
- ∠AFE=∠EDC=90∘\angle AFE = \angle EDC = 90{^\circ}
- ∠FAE=∠DCE, себебі∠FAE=90∘−x, ∠DCE=90∘−x\angle FAE = \angle DCE, \ себебі\ \angle FAE = 90{^\circ} - x, \ \angle DCE = 90{^\circ} - x\(үшбұрыштың ішкі бұрыштарының қосындысы 180∘{^\circ}) .
Олай болса, ∆ AFE = ∆ CDE (II белгі бойынша)
AB=CD=AF=4
BC=AD=AE+ED, AD=5+3=8
Жауабы: AB=4, AD=8.
2-мысал.

Суретте AB=AC, . 1) теңдігін дәлелдеңдер; 2) егер AC=15 см, DC= 5 см болса, онда BD мен AB-ны табыңдар.
Шешуі: 1) Дәлелденуі: шарт бойынша AB=AC және . AD қабырғасы және үшбұрыштарына ортақ қабырға болып тұр. Демек, бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрыш, екінші үшбұрыштың екі қабырғасымен арасында орналасқан бұрышқа тең. Онда, . (I белгі бойынша)
2) Егер , онда оның қабырғалары да тең. Яғни, AB=AC=15см, BD=CD=5см
Жауабы: AB=15см, BD=5см
3-мысал.
Теңқабырғалы үшбұрыштың барлық бұрыштары тең екендігін дәлелдеңдер.
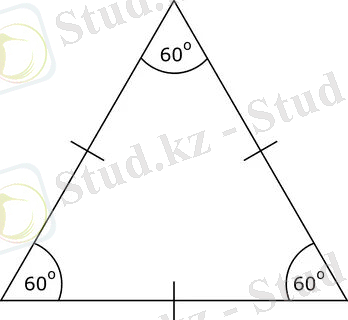
, AB=BC=CA, екендігін дәлелдеу керек.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz