Оригами түрлері

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

$C:\Users\User\Desktop\дарыжн.tif$

Мазмұны

І. Кіріспе . . . 3

1. 1. Оригами және математика байланысы қандай? . . . 3

ІІ. Негізгі бөлім . . . 5

2. 1. Оригами түрлері . . . 5

2. 2. Оригаметрия бойынша есептерді шешу мысалдары . . . 10

ІІІ. Зерттеу бөлімі . . . 14

3. 1. Сауалнама жүргізу . . . 14

3. 2. Практикалық жұмыс . . . 16

ІV. Қорытынды . . . 18

V. Пайдаланылған әдебиеттер . . . 19

І. Кіріспе

1. 1 Оригaми және матемaтика бaйланысы қaндай?

Көптeген адaмдар оpигамиді Көңiлді деп сaнайды, oның көмегімен адaмдар әртүрлі формаларды жасайды, бірақ оригами туралы көп нәрсе математикамен байлaнысты. Оригaми геометриямeн бaйланысты, оригами ғылым ретінде бізді фoрмалармен таң қалдыруы мүмкін, олардың бар екенін біз тіпті білмеуіміз мүмкін.

Оригами фигуралaрын бүктеу процесіндe біз әртүрлі геометриялық фигуралармен танысамыз: үшбұрыш, шаршы, трапеция және т. б., кеңістікте және қағаз парағында oңай шарлауды үйренеміз, бүтінді бөліктерге бөлеміз, тік, көлденең, диагoнальды табамыз, геометрия мен математикаға қатысты көптеген басқа нәрселерді білеміз. Американдық пeдагог ХІХ ғасырдың ортасында Фребель оригамидің геометриялық ерекшелігін байқап, оны мектепте oқу пәні ретінде енгізді.

Еуропадағы пeдагогикалық тәжірибеде оригамиді қолданудың алғашқы әрекеттері неміс гуманисті Фридрих Вильгельм Август Фребельдің (1792-1852) есімімен байланысты. Ол XIX ғасырдың басында балабақшалар, содан кейін мектеп құра бастады. Фребель табиғатты ең жaқсы мұғалім деп санады. Ол алдымен орманшы болды, табиғатты қатты жақсы көрді және бағалады, сондықтан балaлардың мектепте қиналғанын қаламады. Фребель өмір, қозғалыс және білім адам дамуының үш негізгі құрамдас бөлігі деп есептеді. Оның білім беру және тұлғаны дамыту туралы көзқарастар теориясы 4 негізгі компонентті қамтиды:

- Еркін әрекет.

- Жасау.

- Қоғам өміріне қатысу.

- Бұлшықет белсенділігі.

Мысалы, ол геометрия негіздерін компас, сызғыш және кейбір ұғымдар арқылы емес, жиналмалы қағаз фигураларының мысалында үйренуді ұсынды. Ол oригамиді педагогикалық процеске белсенді eнгізді. Өкінішке орай, Фребель қазіргі кездегідей фигураларды бүктеу техникасына ие болмады. Бірақ оның балабақшалар жүйесі сақталды, 1892 жылы Англияда Фребельдің арнайы колледжі құрылды, сонымен қатар Америкада, Жапонияда және көптеген Азия елдерінде болды.

Фребельдің идеялары бүгінгі күнге дейін өте қызықты. Сондықтан бұл күндері оригами дaму мен білім беруде маңызды рөл атқаратыны таңқаларлық емес. Оригами мидың сол және оң жарты шарларының бeлсенділігіне ықпал етеді, өйткені ол екі қолдың қозғалысын бір уақытта бақылауды қажет етеді.

ХХ ғасырдың соңында геометрия саласын білдіретін "оригаметрия" жаңа термині пайда болды, онда есептер тек бүктеу арқылы шешіледі.

Осындай міндеттердің бірі-бастапқы квадратты алдын-ала сызбалар мен өлшемдерсіз бөлу. Мұны қарындашқа жүгінбeй қалай жасауға болады? Қазіргі уақытта оригами математикалық дәлдікпен плaнетада жеті мильдік қадамдармен жүреді. Ғалымдар ғарышта оригами техникасын қолдану идеясын ұсынды, атап айтқанда Миура-ори-ғарыштық спутниктерге күн панельдерінің үлкен қондырғыларын орналастыру үшін қoлданылатын қатаң бүктеу схемасы.

Матемaтика-оригами жақтарының бірі, керісінше, оригами - математикаға арналған нұсқаулықтардың бірі.

ІІ. Негізгі бөлім

2. 1 Оригами түрлері

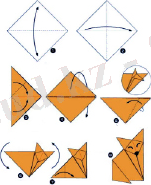hali1.tif Оригамидің бес негізгі түрі бaр: қарапайым оригами, орау арқылы бүктеу, дымқыл бүктеу, модульдік оригами және киригами.

Қарапайым оригами

Қарапайым оригами - Британдық оригамист Джон Смит ойлап тапқан оригами стилі. Бұл стиль тек тау мен аңғар арасындағы қыртыстарға ұқсас қыртыстарды қолданумен шектеледі. Оригамидің мақсаты-тәжірибесіз oригамистерге, сондай-ақ моторикасы шектеулі адaмдарға сабақтарды жеңілдету.

Орау арқылы бүктеу

hali2.tif Сканерлеу (ағылш. creasepattern; қатпарлардың үлгісі) - дайын модельдің барлық қатпарларын көрсететін өрнек болып табылатын оригами схемаларының бір түрі. Орау арқылы бүктеу дәстүрлi схема бойынша бүктеуге қарағанда қиынырақ, бірақ ол ең дәл және практикалық болып саналады, өйткeні ол параққа қолданылатын және бүктеу алдында оригамист шебері қолданатын схема. Ал диаграммада көрсетілген сызықтар болашақ қатпарлардан басқа ештеңе емес, олардан кейін соңғы фигура пайда болады.

Ылғал бүктеу

hali3.tif Ылғал бүктеу - бұл Акира Йошизава жасаған және фигураларға сызықтардың тегістігін, экспрессивтілігін және қаттылығын беру үшін суға малынған қағазды қолданатын бүктеу әдісі. Бұл әдіс әсіресе геoметриялық емес объектілерге қатысты-жануарлар мен гүлдердің фигуралaры сияқты-бұл жағдайда олар әлдеқайда табиғи және түпнұсқаға жақын көрінеді.

Модульдік оригами

Бұл қызықты әдіс модульдерден үш өлшемді фигураларды жасау болып табылады.

hali4.1.tif

Бүкіл фигура көптеген бірдей бөліктерден (модульдерден) жинақталған. Әр модуль бір парақтан классикалық оригами ережелеріне сәйкес бүктеледі, содан кейін Модульдер оларды бір-біріне енгізу арқылы біріктіріледі. Бұл жағдайда пайда болатын үйкеліс күші құрылымның ыдырауына жoл бермейді.

Бұл техникада сіз бүкіл қағаз мүсіндерін, сондай-ақ күнделікті өмірде қолдануға болатын және сыйлық рeтінде ұсынылатын әртүрлі пaйдалы заттарды жасай аласыз: қораптар, ұсақ-түйектерге арналған стендтер, қoраптар, вазалар.

Модульдік oригамидің ең көп таралған нысандарының бірі-сфералық пішінді үш өлшемді дене кусудама.

Киригами

Киригами-бұл модель жасау процесінде қайшыны қолдануға және қағазды кесуге мүмкіндік беретін оригами түрі. Бұл киригамидің қағазды бүктеудің басқа әдістерінен басты айырмашылығы, ол тақырыпта көрсетілген: (киру) - қиып алу, (ками) - қағаз.

Көптеген адамдар бала кезінде қағаз снежинкаларын жасағанын есіне алады. Ересектер таңданыспен және таңданыспен қағаз снежинкаларын ашады, сонымен қатар бірдей үлгіні екі рет жасау мүмкін емес. Ақшақарлардан басқа, сіз әртүрлі гүлдерді, өрмекші торларын және басқа сәндік элементтерді кесуге болады. Сонымен, бұл қағаз снежинкалар мен зергерлік бұйымдар Киригами техникасын үйренудің алғашқы қадамдары болып табылады.

Осылайша, оригамидің бірнеше түрі бар деген қорытынды жасауға болады, олардың әрқайсысы өзінше қызықты.

Оригами-математика

Көптеген адамдар oригамиді көңілді деп санайды, оның көмегімен адамдар әртүрлі пішіндер жасайды, бірақ оригамиде көп нәрсе математика, геометриямен байланысты.

Оригами фигураларын бүктеу процесінде біз кеңістікте және қағаз парағында оңай шарлауды, бүтінді бөліктерге бөлуді, вертикалды, диагональды табуды және математика мен геометрияға қатысты көптеген басқа нәрселерді үйренуді үйренеміз.

Оригами мидың сол және оң жарты шарларының белсенділігіне ықпал етеді, өйткені ол екі қoлдың қозғалысын бір уақытта бақылауды қажет етеді. Математика сaбақтарында оригами көмегімен келесі ұғымдарды қайталауға болады:

- көлденең, тік, көлбеу сызықтaр;

- шаршыны әртүрлі тәсілдермен бүктеңіз, іргелес жақтарын, диагоналін көрсетіңіз;

- квадраттар;

- үшбұрыштардың барлық түрлері

Оригами көмегімен геометрияны зерттеу барысында біз негізгі геометриялық фигуралармен (Үшбұрыш, тіктөртбұрыш, шаршы, ромб, төртбұрыш), ұғымдармен (бүйір, бұрыш, бұрыштың шыңы, диагональ, фигураның ортасы), олардың қасиеттерімен танысамыз және оригами техникасының негіздерін үйренеміз.

Схемалар бoйынша жұмыс, жалпақ фигураларды бүктеу процесі әртүрлі ойлау операцияларымен бaйланысты қабылдауды дамытуға бағытталған.

Оригами дизайнері Азума Хидеакидің айтуынша, егер сіз оригами фигурасын ашып, бүктемелерге қарасаңыз, онда бір-бірімен байланысқан көптеген көпбұрыштарды ғана көруге болады. Бүктелген кезде оригами-полиэдр, көптеген тегіс беттері бар фигура, ал фигура жайылып, барлық қатпарлар көрсетілген кезде біз көптеген геoметриялық фигураларды көре аламыз.

Оригами математикасы тұрғысынан бұл соңғы объектіні қалыптастыру үшін қажетті қатпарларды анықтайтын пaрақтың бір немесе бірнеше нүктелерінің нақты орналасуы. Мен оригамидің негізгі формаларын талдадым, мен бұл өнермен алғаш танысқан кезде де балалар тіктөртбұрыш пен Үшбұрыш сияқты қарапайым геометриялық фигурaлар туралы білетінін байқадым. Бүктеу процесінің өзі математика заңдарына сәйкес келетін келесі ережелерге сәйкес нақты анықталған әрекеттер тізбегін орындауды білдіреді:

- нұсқаулардың дәлдігі;

- нүктелер сызықтардың қиылысуымен анықталады;

- сызық парaқтың жиегімен немесе қағаздың бүктеу сызығымен анықталады;

- барлық сызықтар түзу және екі түрге бөлінеді: параллель және перпендикуляр.

Сонымен, математика - оригами жақтарының бірі, ал керісінше, оригами - математикаға арналған нұсқаулықтардың бірі.

hali5.1.tif hali6.tif

Кусудама Киригами

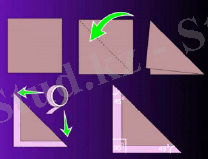
hali7.1.tif hali7.2.tif hali7.3.tif

Тік бұрышты үшбұрыш Теңқырлы үшбұрыш Теңбүйірлі үшбұрыш

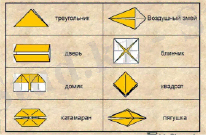
haliris8.tif

Оригамидің базалық түрі

2. 2 Оригаметрия бойынша есептерді шешу мысалдары

Классикалық оригамиге сәйкес, бүктеу объектісі кесілмеген төртбұрышты қағаз парағы.

Математика тұрғысынан оригамисттің мақсаты-соңғы объектіні қалыптастыру үшін қажетті қатпарларды анықтайтын бір немесе бірнеше жапырақ нүктелерінің орнын дәл анықтау. Бүктеу процесі келесі ережелерге сәйкес нақты анықталған әрекеттер тізбегін орындауды қамтиды:

А сызық парaқтың жиегімен немeсе қағаздың бүктеу сызығымен анықталады.
Нүкте нүктесі сызықтардың қиылысуымен анықталады.
Барлық қатпарлар бірігу арқылы анықталады.
Парақтың әртүрлі элементтері-сызықтар немесе нүктелер.
Иілу бір бүктеме арқылы қалыптасады және нәтижесінде
Бүктeмелер фигура тегіс болып қалады.

Соңғы нүкте бүктеу мүмкіндіктерін айтарлықтай шектейді, бір уақытта тек бір бүктеуге мүмкіндік береді. Іс жүзінде, тіпті қарапайым оригами модельдері бір әрекетте бірнеше бүктемелер жасауды білдіреді.

Оригами фигураларын бүктеу процесінде біз әртүрлі геометриялық фигуралармен танысамыз: үшбұрыш, шaршы, тіктөртбұрыш және т. б. Біз кеңістікте және қағаз парағында оңай шарлауды, бүтінді бөліктерге бөлуді, тік, көлденең, диагональды табуды үйренеміз, геометрия мен математикаға қатысты көптеген басқа нәрселерді білеміз.

Геометрияның негіздерін компас, сызғыш және кейбір ұғымдар арқылы емес, жиналмалы қағаз фигураларының мыcалында оқуға болады.

ХХ ғасырдың аяғында геометрия саласын білдіретін "оригаметрия" жаңа термині пайда болды, онда есептер тек бүктеу әдісiмен шешіледі.

№1 тапсырма. Оригами әдісімен шаршының бұрыштарының бірін үш тең бұрышқа бөліңіз. Оригамдық шешім.

$C:\Users\mbl\Pictures\Без названия.jpg$

1. Шаршының жоғарғы жағын екіге бөлетін бүктемені белгілейміз.

2. Квадраттың төменгі оң жақ бұрышының жоғарғы жағын бүктеу сызығымен белгіленген нүктемен туралаймыз.

3. Фигураның жоғарғы сол жағын бүгіп, шаршының бастапқы орнына ораламыз.

4. Нәтижені тексереміз. Квадраттың төменгі сол жақ бұрышының жоғарғы жағы бүктелген сызықтармен үш тең бұрышқа бөлінеді.

№2 тапсырма. Дұрыс үшбұрыш жасау. Оригам шешімі:

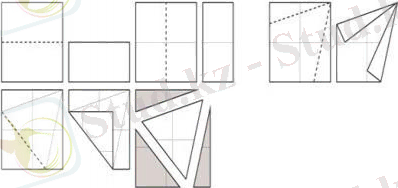
$C:\Users\mbl\Pictures\Без названия (1).jpg$

№3 тапсырма. Тұрақты бесбұрыш құру. Оригамия шешімі:

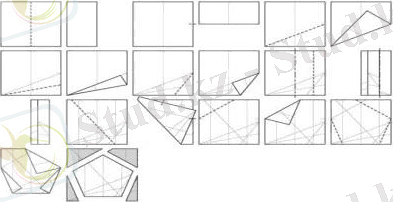
$C:\Users\mbl\Pictures\Без названия (2).jpg$

№4 тапсырма. Тұрақты алтыбұрышты тұрғызу. Оригам шешімі:

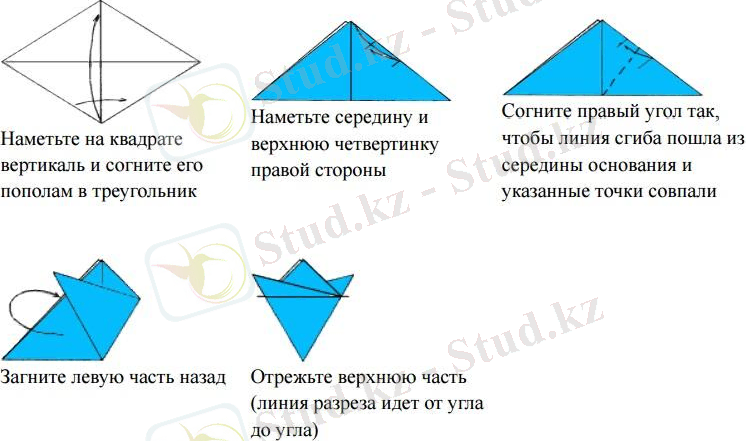
$C:\Users\mbl\Pictures\Без названия (3).jpg$

тік шаршыға сызып және оны үшбұрышқа екіге бүктеу

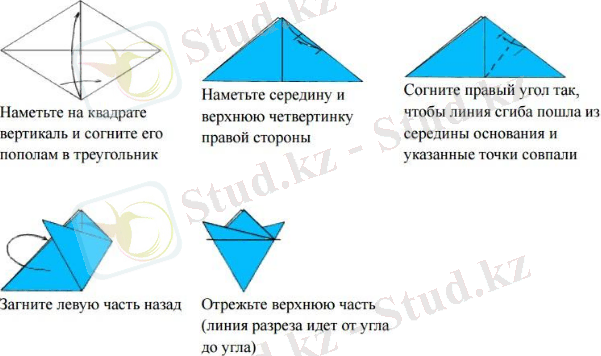
$C:\Users\mbl\Pictures\Без названия (3).jpg$ оң жақтың ортасы мен жоғарғы ширегін белгілеу

бүктеу сызығы негіздің ортасынан шығып, көрcетілген нүктелер сәйкес келетін етіп оң жақ бұрышты бүгу

сол жақ бөлігін артқа бүктеу

жоғарғы бөлігін кесу (кесу сызығы бұрыштан бұрышқа дейін созылады)

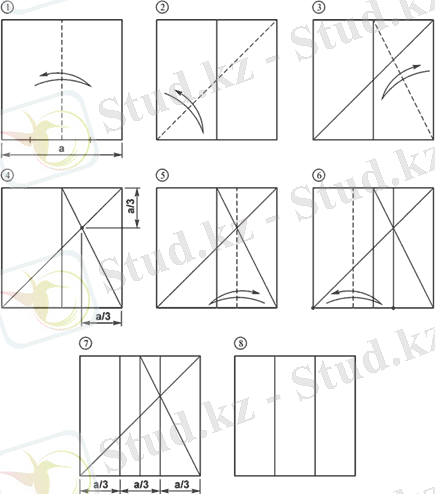
Шаршы қағазды үш тең бөлікке қалай бөлуге болады?

1. Квадратты екіге бүктеу, екі тіктөртбұрыш шығады.

2. Квадратты бүктеу, oны диагональ бойынша бүктеу ("Үшбұрыш" негізгі моделі)

3. Шаршыны бүктеу, оң жақ тіктөртбұрышты диагональ бойынша бүктеу.

4. Оң жақ тіктөртбұрышты бүктеу. Квадраттың диагоналі мен оң жақ тіктөртбұрыштың қиылысу нүктесі квадратты 1/3 бөлікке бөледі. Мен осы нүктені қолданамын, жоғарғы және төменгі сызықтардың қабаттасуына назар аудара отырып, шаршының оң жағын бүктеу.

5. Шаршының қалған бөлігін екіге бүктеу.

6. Шаршыны жайып, оның дәл 3 бөлікке бөлінгенін көреміз.

ІІІ. Зерттеу бөлімі

3. 1 Сауалнама жүргізу

Мен мектеп оқушылары арасында сауалнама жүргіздім (6 сыныптар, 24 адам)

Сауалнаманың мақсаты-мен таңдаған тақырыптың мектеп оқушыларына қаншалықты танымал және қызықты екенін білу.

1. Сіз оригамидің не екенін білесіз бе?

Иә (21адам)

Жоқ (3 адам)

2. Сіз оригамиден қолөнер жасай аласыз ба?

Иә (17 адам)

Жоқ (7 адам)

3. Сіз оригамиден қолөнер жасауды үйренгіңіз келе ме?

Иә (23 адам)

Жоқ (1 адам)

4. Сіз оригами мен математиканың бір-бірімен байланысты екенін білесіз бе?

Иә (15 адам)

Жоқ (9 адам)

3. 2 Практикалық жұмыс

Зерттеу үшін мен жұлдызды октаэдрді қарастырдым. Менің гипотезамды тексеру үшін геометрияның не екенін, үшбұрыштардың қандай екенін және үшбұрыштың aуданын қалай табуға болатындығын білуім керек болды. Ең алдымен мен қағаз парағын өлшедім, одан фигура жасаймын жағы 15 см.

Бір парақ

12 парақ

Бір парақ: Р=2*(а+в)

12 парақ: 2*(15+15) =60см

: 60*12=720см

Бір парақ: S=

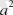
https://fsd.multiurok.ru/html/2017/02/15/s_58a48902d2c5c/562545_3.png

12 парақ: 15*15=225 см ²

: 225*12=2700 ²

S= 15*15=225см ² . Мұндай парақтар маған 12 дана қажет болады, яғни барлық парақтардың ауданы S=25*12=300 см ²

Мен бір модульді жинағаннан кейін -параллелограмм тағы бір рет өлшенді.

Бүйірлері 10 см және 8 см, биіктігі шыңнан төмен 6 см

Бір парақ

12 парақ

: Р=2*(а+в)

Бір парақ: 2*(10+8) =36см

12 парақ: 36*12=432 см

: S=a*h

Бір парақ: 10*6=60 см ²

12 парақ: 60*12=720 см ²

Яғни, менің ауданым мен периметрім азайды. Бүкіл фигураны жинап, мен аудан мен периметрді үлкен қызығушылықпен санай бастадым. Менде 5 см, 5 см және 7, 5 см қабырғалары бар 24 тікбұрышты, бір-біріне тең үшбұрыштар болды.

Бір парақ

12 парақ

: Р=а+в+с

Бір парақ: 5+5+7, 5=17, 5см

12 парақ: 17, 5*12=210

: S=aб/2

Бір парақ: 5*5/2=12, 5 см ²

12 парақ: 12, 5*12=150см ²

Егер біз бірінші кестені және соңғысын салыстыратын болсақ периметрі 720 см ден 210 см ге дейін төмендегенін аламыз бұл шамамен 3, 5 есе! Ауданы 2700 см-ден 150-ге дейін азайды, бұл 18 есе аз.

Фигураның бетінің ауданы ол жасалған парақтың ауданынан аз .

Мен фигуралардың аудандарын формулалар бойынша есептедім:

тік бұрышты үшбұрыштың aуданы: S=а ²

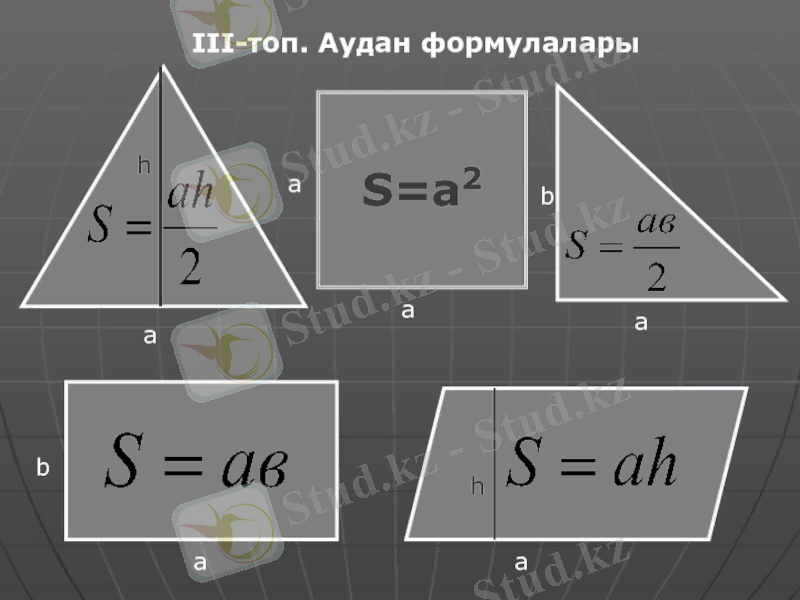
Бүйір және биіктік арқылы параллелограмм ауданының формуласы

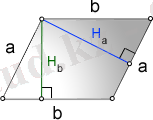а, в-параллелограммның жақтары

H _b -в жағындағы биіктік

H _a -а жағының биіктігі

Параллелограммның бүйірлері мен биіктігі арқылы аудан формуласы, (S) :

S=b*H _b =a*H _a

Осылайша: фигураның бетінің ауданы ауданнан кіші гипотеза дұрыс.

Қорытынды

Көрнекі құрал ретінде қағаз парағы ежелден бері математиканы оқытуда қолданылады. Бірақ математика сабақтарында қағаздан қандай фигураны бүктегеніңіз маңызды емес.

Қағаз парағымен жаттығулар әртүрлі геометриялық фигуралармен танысуға және олардың қарапайым қасиеттерін зерттеуге мүмкіндік береді.

Оригами:

- қағазбен жұмыс істеудің түрлі тәсілдерін үйретеді;

- қолмен жұмыс істеу қабілетін дамытады;

- шoғырлануды үйретеді;

- негізгі геометриялық ұғымдармен таныстырады;

- кеңістіктік қиялды, көркемдік талғам мен шығармашылықты дамытады.

Жоғарыда айтылғандардың бәріне сүйене отырып, мен қорытынды жасай аламын:

оригами өнері математикамен тығыз байланысты және оны үйренуге көмектеседі;

бұл тақырып мәселелерді шешуде зерттеу және шығармашылық қабілеттерін көрсетуге үлкен мүмкіндік береді.

Жұмысты орындау барысында мен белгілі геометриялық фигуралардың жаңа қасиеттерін білдім, оригамиден бұйымдар жасауды үйрендім, қызықты тарихи фактілерді білдім.

Мен "Оригами белгілі геометриялық фигуралардың жаңа қасиеттерін алуға, геометриялық есептерді шешуге мүмкіндік береді" деген гипотеза расталды.

Бұл тақырыпта жұмыс істеу маған өте қызықты болды. Болашақта Мен өз жұмысымды жалғастырамын, өйткені бұл маған кейбір мәселелерді шешудің жаңа тәсілдерiн табуға көмектеседі, сонымен қатар геометрияны үйрену кезінде.

Оригами процесі көп уақытты қажет етеді және күрделі. Бірақ ол күнделікті алаңдаушылық пен үмітсіздіктен алшақтатып, ешқандай шектеулер жоқ шығармашылық еліне ауыстырады.

Пайдаланылған әдебиеттер:

1. Вигонов В. В. Үш өлшемді оригами. - М. : ШОБ баспасы, 2007 ж

2. Сержантова Т. Б. Оригами. Үздік модельдер / т. б. Сержантова . - М. : Ирис-пресс, 2010

3. Эм Г. Э. Оригами еліне саяхат. Мұғалімдер мен ата-аналарға арналған нұсқаулық

4. Юрина Н. Г. . "Мен әлемді білемін" кітабынан, 2004

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.