Санау жүйелері мен цифрлық логиканың негіздері: түрлендірулер, арифметика және комбинациялық схема жобалау (курстық жұмыс)


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНІСТРЛІГІ
М. Әуезов атындағы Оңтүстік Қазақстан Универстиеті
Кафедра
КУРСТЫҚ ЖҰМЫС
17 нұсқа (2 тобы)
Орындаған: Молчанова И.
Группа: ИП-21-7TK
Қабылдаған:
Шымкент 2023
Мазмұны
Кіріспе . . . 3
№1 тапсырма. Санақ жүйелер . . . 4
- Он алтылық санақ жүйесінде берілген сандарды ондық жүйеге аудару . . . 4
- Екілік сандарды сегіздік және он алтылық санақ жүйелеріне аудару . . . 6
- Сегіздік сандарды екілік жүйеге аудару . . . 8
- Он алтылық сандарды екілік сандарға түрлендіру . . . 9
- Ондық сандар үшін екілік эквивалентті табу . . . 10
- Екілік сандарды ондық сандарға аудару . . . 11
Кіріспе
Бүгінгі таңда ақпараттық технологиялармен қоршалған қоғамда әртүрлі санау жүйелері арасындағы сандарды түсіну және аудару қабілеті үлкен маңызға ие. Кез-келген салада әр түрлі санау жүйелерінде сандармен жұмыс істей білу күнделікті есептеу мен деректерді талдаудың ажырамас бөлігі болып табылады. Ақыр соңында, кез-келген инновация сандарға негізделген бағдарламалаусыз қажет екенін бәрі біледі.
Бұл курстық жұмыстың мақсаты-өзара аударманың цифрлық жүйелерін талдау әдістерін әзірлеу, сонымен қатар оларды зерттеу: екілік, сегіздік, ондық және он алтылық жүйелер. Олардың әрқайсысының ерекшеліктерін түсіну, сондай-ақ олардың арасындағы сандарды дұрыс түрлендіре білу дәлірек есептеулер жүргізуге, есептерді шешуді жеңілдетуге және сенімді сақтау мен деректер алмасуды қамтамасыз етуге мүмкіндік береді.
Бұл жұмыста біз әртүрлі санау жүйелері арасындағы сандарды түрлендірудің негізгі ережелерін қарастырамыз, сонымен қатар алынған білімді практикалық есептерге қолданамыз. Осы тақырыпты зерттей отырып, оқырман тек теориялық білімді ғана емес, сонымен қатар күнделікті өмірде және кәсіби қызметте пайдалы дағдыларды алады.
№1 тапсырма. Санақ жүйелер
- Он алтылық санақ жүйесінде берілген сандарды ондық жүйеге аударыңыз
Он алтылық санау жүйесі (немесе 16 - база) - информатика мен бағдарламалауда кеңінен қолданылатын ең танымал позициялық санау жүйелерінің бірі. 0-ден 9-ға дейінгі сандардан басқа, бұл жүйе 10-нан 15-ке дейінгі сандарды көрсету үшін A, B, C, D, E және F әріптерін қолданады. Сандарды он алтылықтан ондыққа түрлендіру компьютерлерде сақталған деректермен жұмыс істеу кезінде немесе бағдарламалау кезінде маңызды мәселе болып табылады.
Он алтылық санау жүйесі-бұл атауынан көрініп тұрғандай 16 негізі бар позициялық санау жүйесі. Бұл санау жүйесінің сандары 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 және латын әріптері А-дан F-ге дейін, A, B, C, D, E, F әріптері келесі мәндерді көрсету үшін қолданылады: 1010, 1110, 1210, 1310, 1410, 1510. Сандарды он алтылық санау жүйесінен ондық санға түрлендіру-бұл енгізу және түрлендіру, сондай-ақ деректерді сақтау үшін қолданылатын өте кең таралған операция. Сондықтан мен мұны қалай жасау керектігінің мысалын төменде қарастырамын.
Санды он алтылықтан ондық санға түрлендіру үшін сізге қажет: алдымен он алтылық санның әр санының реттік нөмірін анықтаңыз. Санау тәртібі әрқашан 0 және оң жақтан басталады (төмендегі практикалық мысалда көрсетілгендей) .
Егер оналтылық жүйенің мағынасында латын әріптері болса, олардың мәндерін сәйкес әріптермен ауыстырыңыз. Содан кейін мен әр санды санның реттік санына сәйкес келетін дәрежеде 16-ға көбейтемін.
Соңғы нәтиже ондық санау жүйесіндегі эквивалент болып табылады.
Тапсырма: C97D. 3A
Шешуі:
C97D. 3А 16 = (12*16 3 +9*16 2 +7*16 1 +13*16 0 +3*16 -1 +10*16 -2 ) 10 =(49152+2304+ 112+13+0, 8125+0, 03906525) 10 =51581, 8164 10
Жауабы: C97D. 3A 16 =51581, 8164 10
1. 2 Екілік сандарды сегіздік және он алтылық санақ жүйелеріне аудару
Тек екі мүмкін мәнді қолданатын екілік санау жүйесі - 0 және 1 - информатика мен цифрлық электроникада, сондай-ақ бағдарламалауда кеңінен қолданылады. Бұл тек екі сан сияқты көрінуі мүмкін, бірақ комбинациялар көп болуы мүмкін. Дегенмен, ұзақ жазбалары бар сандық жүйелерді (мысалы, екілік) пайдалану жиі ыңғайсыз болуы мүмкін. Сондықтан сандарды екілік, сегіздік және он алтылық сандарға түрлендіру бағдарламалаумен жұмыс істеу кезінде өте маңызды операция болып табылады.
Екілік санау жүйесінен сегіздікке түрлендіру:
Санды екіліктен сегіздікке түрлендіру үшін екілік санды оң жақтан бастап үш саннан тұратын топтарға бөлу керек. Егер соңғы топта үш саннан аз болса, солға нөлдер қосыңыз. Содан кейін әр топты екілік форматтағы үш цифрдан сегіздікке бір цифрға түрлендіріңіз.
Екілік-он алтылық түрлендіру: санды екілік саннан он алтылыққа түрлендіру үшін алдымен оны ондық санау жүйесіне түрлендіру керек. Содан кейін оны он алтылық немесе сегіздік етіп өзгертуге болады.
Мен мұны іс жүзінде қалай жасау керектігін қарастырамын.
Тапсырма: 110. 10101 2
Шешуі:
110. 10101 2 =(1*2 6 +1*2 1 +1*2 -1 +1*2 -3 +1*2 -5 ) 10 =(64+2+1/4+1/8+1/32) 10 =66. 40625 10
Енді біз екіліктен ондыққа ауыстырдық, қалған жүйелерге аудара аламыз.
Ондықтан сегіздік жүйеге:
0, 4062*8=3, 2496
0, 2496*8=1, 9968
0, 9968*8=7, 9744
0, 9744*8=7, 7952
66. 40625 10 =102, 3177 8
Ондықтан он алтылыққа:
0. 4062*16=6. 4992
0. 4992*16=7. 9872
0. 9872*16=15. 7952
0. 7952*16=12. 7232
66. 4062510=42, 67FC 16
Жауабы: 110. 10101 2 =102, 3177 8 =42, 67FC 16
1. 3 Сегіздік сандарды екілік жүйеге аудару
Сегіздік санау жүйесі-ақпараттық жүйелерде жиі қолданылатын тағы бір маңызды жүйе. Бұл 0-ден 7-ге дейінгі сандарды қолданатын 8 негізгі жүйе.
Сигналды сегіздік санау жүйесінен екілік санға түрлендіру үшін мен оны алдымен ондық санға түрлендіремін, содан кейін сол жерден екілік санға түрлендіремін. Мұнда мен аударма үшін бірдей амалдарды қолданамын-бөлу және көбейту.
Іс жүзінде бұл келесідей болады:
Тапсырма: 713, 21 8
Шешуі:
713, 21 8 =(7*8 2 +1*8 1 +3*8 0 +2*8 -1 +1*8 -2 ) 10 =(448+8+3+2/8+1/64) 10 =459. 266 10
Енді біз сегіздіктен ондыққа ауыстырдық, келесі жүйеге аудара аламыз.
1
459. 266 10 =111001011. 0110 2
Жауабы: 713, 21 8 =111001011. 0110 2
1. 4 Он алтылық сандарды екілік сандарға түрлендіру
Бұрын түсіндіргенімдей, он алтылық санау жүйесі-бұл он алтылық таңбаларды қолдануға негізделген позициялық санау жүйелерінің бірі: 0-ден 9-ға дейінгі сандар және латын әріптері А-дан F-ге дейін. ал цифрлық технология жазудаактамырақ және кенеттен пайда болса, қатені қолмен нақтылау және табу оңайырақ.
16-шы санау жүйесін түрлендіру принципі: сандарды он алтылықтан екілікке түрлендіріңіз, ондық санау жүйесіне түрлендіріңіз. Осыдан кейін ғана алынған мәнді екілік кодқа түрлендіруге болады.
Енді мен тағы да практикалық мысал келтіремін:
Тапсырма: E33. 75 16
Шешуі:E33. 75 16 =(14*16 2 +3*16 1 +3*16 0 +7*16 -1 +5*16 2 ) 10 =(584+48+3+0. 438+0. 0195) 10 = =3635. 458 10
Қазір он алтыдан онға ауыстық, келесі жүйеге көшуге болады.
3635. 458 10 =111000110011. 011 2
Жауабы: E33. 75 16 =111000110011. 011 2
1. 5 Ондық сандар үшін екілік эквивалентті табу
Мен бұған дейін екілік санау жүйесі - бұл сандар тек екі цифрмен ұсынылатын 2 негізі бар позициялық санау жүйесі: 0 және 1. Бұл жүйе компьютерлерде және цифрлық электроникада кеңінен қолданылады, мұнда деректер мен ақпарат екілік сандар ретінде сақталады және өңделеді. Дегенмен, деректерді талдау мен визуализацияны жеңілдету үшін кейде екілік сандарды ондық сандарға түрлендіру қажет. Мұны істеу үшін аударма принципін қарастырыңыз: екілік сандарды ондыққа айналдыру үшін мен бөлу операциясын орындаймын. Мұндай бөлінудің мысалдары жоғарыда талқыланды.
Тапсырма: 637, 14 10
Шешуі:
0, 14*2=0, 28
0, 28*2=0, 56
0, 56*2=1, 12
0, 12*2=0, 24
Жауабы: 637, 14 10 =10001, 0010 2
1. 6 Екілік сандарды ондық сандарға аудару
Бүгінгі таңда ең көп таралған санау жүйесі-10 негізі бар ондық санау жүйесі. Адам бағдарламашылары ондық сандарды қолмен қолдануға ыңғайлы болғанымен (аударма және басқа сандық операциялар үшін), компьютерлер мен сандық электроника негізінен екілік санау жүйесімен жұмыс істейді. Тек екі цифрды қолданатын санау жүйесі: 0 және 1. Сондықтан ондық сандардың екілік эквивалентін табу информатика мен бағдарламалауда маңызды рөл атқарады.
Екіліктен ондыққа түрлендіру үшін көбейту операциясын қолданамын.
Тапсырма:10101 2
Шешуі:
10101 2 =(1*2 4 +1*2 2 +1*2 2 +1*2 0 ) 10 =(16+4+1) 10 =21 10
Жауабы: 10101 2 =21 10
- Келесі ондық сандарды екілік, сегіздік және он алтылық сандарға түрлендіріңіз:
Ондық санау жүйесінен бірден үш басқаға - екілік, сегіздік және он алтылық санау жүйесіне түрлендіру қажет. Сандарды ондық санау жүйесінен түрлендіру үшін әдеттегідей бөлу операциясын қолданамыз. Әрбір жүйе үшін бөлгіш жеке болады. Мысалы, ондық жүйеден екілік жүйеге көшу үшін қалдық 1 немесе 0 болғанша 2-ге бөлу керек. Сосын сегіздік санау жүйесіне айналдыру үшін қалдық аз болғанша 8-ге бөлу керек. сегізден артық. Біз он алтылық жүйеге аударумен де солай істейміз және әрбір аударманың жауабы соңынан бастап жазылады.
Тапсырма: 80 10
Шешуі:
80 10 =101 2
80 10 =120 8
80 10 =50 16
Жауабы: 80 10 =101 2 =120 8 =50 16
№ 2 тапсырма. Арифметикалық операциялар.
2. 1 Екілік сандардың арифметикалық амалдарын орындаңыз:
Қосу, алу және көбейтудің логикалық амалдары математикалық операциялардан ерекшеленеді. Бұл тапсырмада біз мұны анық растай аламыз; қосу амалын қарастырамыз. Өздеріңіз білетіндей, логикалық 1+1=10, 0 жазып, 1 тасымалдаңыз. Логикалық 0+0=0, 1+0=1, 0+1=1. Осы ережелерді қолдана отырып, екілік санау жүйесіндегі тапсырмадағыдай қосу амалын орындауға болады.
Тапсырма: 000 2 +10 2
Шешуі:
111000
10
1100111
Жауабы: 000 2 +10 2 =1100111 2
2. 2 Ондық сандарды 8421 BCD кодына түрлендіріп оларды қосыңыз:
Ең алдымен, біз 8421 BCD кодының тұжырымдамасын енгіземіз. Бұл цифрлық құрылғылардың санау жүйесіндегі екілік-ондық код нұсқаларының бірі. Бұл кодты пайдаланған кезде ондық сандар екілік кодта жазылады - жеке цифрдың әрбір цифры төрт бит арқылы жазылады.
Тапсырма: 36+74
Шешуі:
Бұл тапсырманы орындау үшін алдымен ондық жүйеде берілген рационал сандарды 8421 BCD кодына сәйкес екілік санау жүйесіне аударамын.
8421 BCD кодта:
36 10 =0011 0110 2
74 10 =0111 0100 2
Алынған сандарды бағанға қосу керек, өйткені біз қосу әрекетін орындадық.
0011 0110
0111 0100
1010 1010
Нәтижесінде біз әр санат үшін тыйым салынған комбинацияларды алдық. Олар тыйым салынған деп аталады, өйткені олар оннан он беске дейінгі сандарды білдіреді және ондық жүйе үшін бұл мүмкін емес және қабылданбайды. Сондықтан мұндай кодтан құтылу үшін біз түзету кодын қосамыз. Бұл код ондық жүйедегі 6 цифры немесе ондық жүйедегі басқаша 0110 цифры (8421 BCD кодына сәйкес) .
1010 1010
0110
1011 0010
0110
00010001
Енді біз кодты алдық, мен оны ондық жүйеге қайта аударамын. Әр цифрдың соңынан 4 цифрды бөлемін, цифрлар жеткіліксіз болса 0-ді қосамыз.
0001. 0001. 2 =110 10
Санды ондық жүйеде алдық. Осылайша, 8421 BCD кодын пайдаланып сандарды аудару және олармен әртүрлі логикалық операцияларды орындау оңай.
Жауабы: 36+74=110
2. 3 Қосымша код әдісін қолдана отырып таңбасы бар сандардың арифметикалық амалдарын орындаңыз:
Ондық жүйенің теріс сандарын осылайша қосуды орындау үшін ең алдымен осы сандарды екілік санау жүйесіне аудару қажет. Содан кейін теріс санды білдіретін қосымша кодты алу үшін алынған екілік кодты қолданамын. Ал қосымша код болуы үшін мен санды кері екілік кодқа түрлендіремін. Мұндай цифрлық аударманың мағынасы ауыстыру болып табылады (егер ол 1 болса, ол 0 болады және керісінше) . Енді кері код бар, ол тек қосу әрекетін орындау үшін қалады және енді қосымша код дайын. Екі сан да теріс, сондықтан біз әрқайсысы үшін қосымша кодтарды тауып, оларды әдетте екілік сандармен жасайтындай бағанға қосамыз. Алынған жауап - ондық жүйеге түрлендіру қажет сан.
Тапсырма: (-89) +(-14)
Шешуі:
89 10 =1011001 2
14 10 =1110 2
тікелей код- 1011001 2
артқа код- 0100110 2
тікелей код- 1110 2
артқа коды- 0001 2
қосымша код:
0100110
1
0100111
0001
1
0010
қосуды орындаймыз:
0100111
0010
0101001
0101001 2 =1*2 5 +1*2 3 +1*2 0 =(32+8+1) 10 =41 10
Жауабы: (-89) +(-14) = 41 10
№ 3 тапсырма. Логикалық алгебра.
3. 1 Логикалық алгебра теоремаларын қолдана отырып келесі өрнектерді жеңілдетіңіз:
Бұл тапсырманы орындау үшін біз өрнекті жеңілдетуіміз керек. Математикалық әрекеттер мен топтастыру заңдарын, сонымен қатар логикалық алгебраның негізгі ережелерін қолданамын. Мысалы, мұндай заңдарға қайталану заңы (немесе басқаша түрде тавтология заңы), үшіншіні алып тастау заңы, қос терістеу заңы, жұтылу заңдары, коммутативтілік заңы, де Морган заңы, ассоциативтілік заңы, жалпылама желімдеу заңы, үлестіргіштік заңы, логикалық қайшылық заңы және т. б. Әрине, олар әлдеқайда көп, бірақ біз жеңілдету үшін осы негізгілердің бірнешеуін қолданамыз.
Тапсырма: F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3
Шешуі:
F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 =x 1 x 2 x 3 +x 1 x 2 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 =x 1 x 4 (x 2 +x 2 x 3 ) +x 1 (x 2 x 3 +x 2 x 3 x 4 ) = x 1 x 2 x 4 +x 1 x 3 x 4 +x 1 x 2 x 3 +x 1 x 2 x 3 x 4
Жауабы: x 1 x 2 x 4 +x 1 x 3 x 4 +x 1 x 2 x 3 +x 1 x 2 x 3 x 4
3. 2 Берілген өрнек бойынша ақиқат кестесін құрыңыз және жеңілдетіңіз:
Тапсырма ақиқат кестесін құруды айтады. Жалпы алғанда, информатикада және цифрлық құрылғыларда ақиқат кестесі түсінігі логикалық функцияны сипаттауға көмектеседі. Әрбір ұяшық кездейсоқ таңдалмаған белгілі бір тағайындалған орынды алады. Ақиқат кестесіндегі әрбір 0 немесе 1 берілген функцияның алгебралық көбейтіндісін көрсетеді. Алдымен тапсырмадағы қолжетімді функцияға сәйкес кестені толтыру үшін біз нөлдер қай жерде болуы керек және қай жерде болуы керек екенін анықтаймыз. Ол үшін функция мүшелерінің әрқайсысы әртүрлі вариацияларда 0 немесе 1 қабылдай алатын барлық мүмкін мәндерді таңдаймыз. Біз мұны тапсырмадағы F функциясының әрбір мүшесімен орындаймыз. Содан кейін алынған сандарды ақиқат кестесіне белгілі бір ретпен енгіземіз және мұндай кестені оңайлату оңай болады. Мұнда логикалық функцияларды түрлендіру заңдылықтарын да қолдануға болады - менің нақты тапсырмам үшін үшіншісін алып тастау заңын қолданамын.
Тапсырма: F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 3
Шешуі:
x 3 +x 1 x 2 +x 1 x 2
F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 3 = x 3 +x 1 x 2 +x 1 x 2
Жауабы: F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 1 x 2 x 3 +x 3 = x 3 +x 1 x 2 +x 1 x 2
3. 3 Карно картасы бойынша логикалық өрнектер жасаңыз:
Логикалық функциялар деп аталатындар бар. Ыңғайлы және жеңілдетілген көрсетілім үшін Карно карталары әдетте қолмен қолданылады (немесе басқа жолмен, Вейтч картасы) . Жалпы мұндай карта ақиқат кестесі болып табылады. Бұл кестеде менің тапсырмама сәйкес 0 және 1 цифрлары бар 16 ұяшық бар. x 1 және x 2 мәндері көлденеңінен берілген. Тігінен - x 3 және x 4 . Қиылысында ұяшық бар және ондағы цифрға байланысты функцияның әрбір мүшесі үшін мәнді немесе инверсиясы бар бірдей мәнді тағайындаймыз. Мұндай инверсия сызықша ретінде белгіленеді (мысалы, х ) . Осылайша, кестедегі әрбір фигураны бояу керек. Менің тапсырмамдағыдай қатар тұрған төрт бірлік аламыз. 8 ұяшықты олар жақын емес немесе бұрышта орналасқан кезде алатын жағдайлар бар. Сонымен, біз жасаған жұмыстан кейін алынған өрнекті жеңілдету жеткілікті болады. Мұны логикалық формулалар арқылы жасауға болады. Ал енді жоғарыда айтылғандардың барлығын мысалмен қарастырамын.
Тапсырма:
00 01 11 10
00
01
11
10
Шешуі:
F(x 1 , x 2 , x 3 , x 4 ) =x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 =x 1 x 3 +x 1 x 2 x 3
Жауабы: x 1 x 3 +x 1 x 2 x 3
№ 4 тапсырма. Комбинациялық логикалық схемаларды жобалау
4. 1 3. 2-тапсырмада алынған өрнек үшін екі кірісті ЖӘНЕ - ЕМЕС элементті пайдаланып, комбинациялық логикалық схеманы құрыңыз.
Әртүрлі типтегі логикалық элементтер бар: механикалық, электромеханикалық, электронды, пневматикалық, гидравликалық, оптикалық және т. б. Олар әртүрлі есептеу жүйелеріндегі ақпаратты түрлендіруге, сонымен қатар онымен әртүрлі операцияларды орындауға қызмет етеді. Мысалы, екілік немесе ондық жүйеде және т. б. Бұл тапсырмада логикалық элементтерден схеманы құрастыру керек ЖӘНЕ - ЕМЕС. Ол үшін конъюнктура функциясының инверсиясын қолданамыз. «ЖӘНЕ-ЕМЕС» операциясының да басқа атауы бар - Шеффердің штрихті. Кез келген кіріс саны бар ЖӘНЕ - ЕМЕС үшін мнемоникалық ереже келесідей естіледі - шығыс: «1» болады, егер кем дегенде бір кірісте «0» болса ғана, «0» барлық кірістерде «1» болса ғана . Бұл элементтің белгіленуін төмендегі орындалған тапсырмада көруге болады. Элементтердің әрқайсысында 2 кіріс және 1 шығыс бар. Бастапқыда бізде 3 ақпарат көзі бар. Бұл x 1 , x 2 және x 3 . Сондықтан 3. 2-тапсырмадағы функцияға қарап, кейбір мәндер үшін инверсияны қолданамыз. Біз схеманы бар өрнекке сәйкес элементтерді бір-біріне көбейту операциясымен жинаймыз.Тапсырма:
x 3 +x 1 x 2 +x 1 x 2
Шешуі:
x 3 +x 1 x 2 +x 1 x 2 = x 3 *x 1 x 2 *x 1 x 2
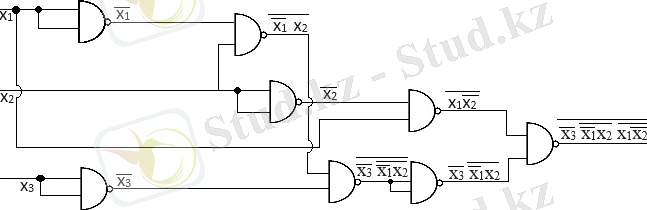
4. 2 3. 2-тапсырмада алынған өрнек үшін екі кірісті НЕМЕСЕ - ЕМЕС элементті пайдаланып, комбинациялық логикалық схеманы құрыңыз.
Жоғарыда айтып өткенімдей, логикалық элементтер кез келген ақпаратпен операциялардың диаграммаларын құру үшін қолданылады. Енді мен НЕМЕСЕ - ЕМЕС операцияларымен осындай схеманы жасау міндетін атқарамын. Бұл дизъюнкция функциясының инверсиясы деп аталады. Басқаша айтқанда, «НЕМЕСЕ-ЕМЕС» операциясы Пирс көрсеткі деп аталады. Оның мәні мынада: біріншіден, «1» егер «0» барлық кірістерге әрекет етсе ғана. Екіншіден, егер кем дегенде бір кірісте «1» болса ғана, «0». НЕМЕСЕ элементі логикалық схемада басқаша белгіленбеген - мұны төменде тапсырмада көруге болады. Мұнда да элементтердің әрқайсысында екі кіріс және бір шығыс бар. Дизъюнкция функциясының инверсиясының көмегімен 3. 2-тапсырмадан функция схемасын құрастыра аламыз. Бұл тапсырмада элементтерді қосу операциясымен. Тапсырма: x 3 +x 1 x 2 +x 1 x 2 Шешуі: ... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz