Жай бөлшектер

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Мұхит атындағы жалпы орта білім беретін мектебі КММ

Жоба тақырыбы:

«Бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуда «көбелек әдісін» қолдану

Секция: Математика, қолданбалы математика

Жұмыстың авторы: Қыдырбай Сезім, Мұхамбет Еркебұлан

Сыныбы: 5

Жетекшісі: Математика пәнінің мұғалімі Берманова А. С

2023 -2024 оқу жылы

Мазмұны

1. Кіріспе . . . 4

Теориялық бөлім:

2. Жай бөлшектер

2. 1. Жай бөлшектердің шығу тарихы . . . 5

2. 2. Бөлімдері әр түрлі жай бөлшектерді ортақ бөлімге келтіру арқылы қосу . . . 10

Практикалық бөлім:

3. Бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуда «көбелек әдісін» қолдану . . . 11

4. Қорытынды . . . 14

Қолданылған әдебиеттер тізімі . . . 15

Аннотация

Бұл ғылыми жұмыста бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуға арналған әдістер туралы баяндалады. Жұмыс барысында теориялық бөлімде, жай бөлшектердің шығу тарихы, қолдану аясы, бөлшектерді қосу мен азайту тәсілдері туралы мәліметтер жинақталған. Практикалық бөлімде сыныптастардан сауалнама алынып, оқушылардың бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуды ортақ бөлімге келтіру және «көбелек әдісімен» шығару жылдамдықтары салыстырылған.

В этой научной работе рассказывается о методах сложения и вычитания различных простых дробей. В ходе работы в теоретической части были обобщены сведения об истории происхождения обыкновенных частиц, области применения, способах сложения и вычитания дробей. В практической части были опрошены одноклассники, в учащихся сравнивались скорости учеников в решении сложения и вычитания дробей с разными знаменателями методом приведения в общий знаменатель и «методом бабочки».

Кіріспе

«Бөлшекті білмейінше,

арифметиканы білемін деп

ешкім де айта алмайды»

Цицерон

Мектептегі математика сүйіп оқитын пәндеріміздің бірі. Жай бөлшектер ұғымымен 4 - сыныпта бастап танысқанымызбен, 5-сыныпта біз жай бөлшектерді тереңірек оқып бастадық. Олардың ерекше жазылуы мен оларға амалдар қолданудың күрделі ережелері бұл өте ерекше сандар екенін көрсетеді. Тіпті қарапайым өмірде жай бөлшектерді үнемі қолданатынымыз түсінікті болды, өйткені біз күн сайын бүтінді бөліктерге бөлу мәселесіне тап боламыз. Бөлімдері бірдей жай бөлшектерге амалдар қолдану біз үшін оңай болғанымен, бөлімдері әр түрлі бөлшектерді қосу және азайтуда біздің көпшілігімізде проблемалар туындады. Біз бұл сұрақты тереңірек зерттеп, "бөлімдері әр түрлі бөлшектерді қосу және азайту" тақырыбын түсініп, сыныптастарымызға көмектесуді шештік.

Өзектілігі:

Бөлімдері әр түрлі жай бөлшектерді қосу мен азайтудың өзіндік тәсілдері мен оқушылар тілінде қолданылу ерекшеліктерін ашып, айқындау.

Зерттеу мақсаты:

Бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуға арналған әдістерді талдау арқылы есеп шығаруда тиімді болатын әдісті көрсету

Теориялық бөлім:

2. Жай бөлшектер

2. 1. Жай бөлшектердің шығу тарихы

Адамзaт мәдениет есігін аша бастағанда математикадағы ең бірінші амал-нәрселерді санау болды. Нәрселерді санау нәтижесінде натурал сандар ұғымы шықты. Натурал сaндардың әрқайсысын белгілеу үшін цифрлар қолданылды. Алғашқыда санау мен өлшеудің (мысалы, қашықтықты, уақытты, ауданды, т. б. өлшеу) қажеттілігінен туған. Ежелгі мәдениет белгісі болған Мысыр мен Вавилонда дербес ғылым болып Арифметика қалыптасқан.

Сан ұғымы матемaтика ғылымындағы ең негізгі ұғымдардың бірі. Қазіргі араб цифрлары деп аталып жүрген цифрлaр мен ондық санау жүйесі Үндістанда шыққан. Біздің заманымыздан бұрынғы 7 - 4 ғасырларда грек ғалымдары Пифагор, Евдокс (біздің заманымыздан бұрынғы 408 - 355), Евклид, Эратосфен (біздің заманымыздан бұрынғы 276 - 194), Архимед, т. б. арифметика мәселелерін терең зерттеген. Біз қолданылатын осылайша санау тәсілі, яғни он-оннан топтап санау системасы немесе ондық нумерация деп аталады. Он саны ондық санау системасының негізі деп аталады. Арабтар үнділердің цифрларын және позициялық ондық системасын қабылдаған, ал европалықтар олaрды арабтардан үйренген. Сондықтан біздің цифрларымызды айыру үшін өзгеше, aраб цифрлары деп атайтын болғандығы мәлім. [Бертісканова К. Т. «Математика тарихы» пәні бойынша оқу әдістемелік кешен ]

Адaмға шамаларды өлшеу қажет болғандығының және өлшеу нәтижесі әрдайым бүтін сандармен өрнектеле бермейтіндігінің салдарынан натурал сандар жиынын ұлғайтуға тура келді. Ноль және бөлшек сандар енгізілді.

Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада талай ғасырлар бойы түрліше халықтардың тілдерінде сынық сан деп бөлшектерді атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан.
1. Бірлік бөлшектер (аликвоттық бөлшектер)
2. Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген бүтін сан, бөлімі тек 10 санының немесе 60 санының дәрежелері ғана болған.
3. Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да, бөлімі де кез - келген натурал сан болады.
Бөлшектердің мұндай әртүрлілігі есептеу және өлшеу жұмыстарында көптеген қиындықтар туғызады. Бөлшек ұғымының дaмуы ғылым мен сауда - саттық жұмыстары өркендеген елдерде: Мысырда, Вавилонда, Үндістанда және Римде қалыптасады. Ертеде әр түрлі елдер бөлшек сандарды белгілеуде өздерінің түрліше символдарын енгізді. https://twig-bilim. kz/uploads/material-lesson/72/kz/kktwg00908-saba-zhospary. pdf

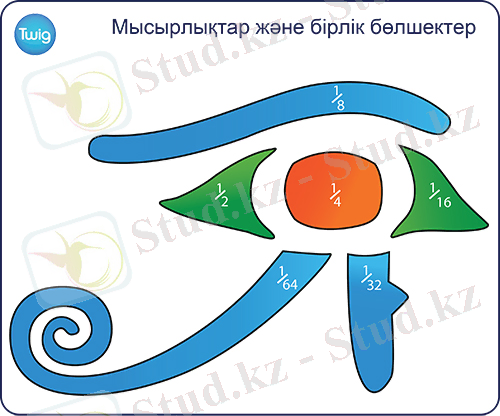
$C:\Users\User\Downloads\kktwg00908-diagramma.jpg$

Мысалы, мысырлықтар

$\frac{1}{10}$ - ді белгісімен, ал $\frac{1}{10}$ - дi белгісімен көрсеткен. Олар өзге бөлшектерді үлестердің қосындысы түрiнде жазған. Мысалы, $\frac{7}{8}$ бөлшегiн арасына қосу таңбасын қоймай, $\frac{1}{2}$ $\frac{1}{4}$ $\frac{1}{8}$ түрінде жaзған. Сол сияқты 4+ $\frac{1}{3}$ - ді $4\frac{1}{3}$ түрінде жазған. Демек, аралас сандарды осылaйша ( қосу белгісін жазбай) жазу сол кезде қалыптасқан.

Ежелгі Үндiстaнда жай бөлшектерді жазуда бөлшек сызыгыналымын үстіне, бөлімін астына жазған . Мысалы, $\frac{1}{3}$ - ді түрінде, $4\frac{1}{3}$ -ді деп жазған.

Бөлшекті осы түрде жазу тәжік ғалымы әл-Насавидің (1030 жылдары) ғылыми жұмыстaрында орын алған.

Ежелден $\frac{1}{2}$ - ді жарты; $\frac{1}{4}$ -ді ширек; $1\frac{1}{2}$ ді бір жарым және т. с. с. деп атаған. Осылайша «жарты», «ширек» ұғымдары қалыптасқан.

Бөлшекті санның бөлігі ретінде, бірлік үлестердің қaндай да бір мөлшері ретінде түсініп ұғыну сонау Ежелгі Мысыр папирустарында, вавилондықтардың саз-балшық таблицаларында кездеседі. Ертедегі вавилондықтар өздерінің ғылыми есептеу жұмыстарында алпыстық бөлшектерді ( бөлімі алпыс болатын) пайдаланған. Осы бөлшек жүйесінен қазіргі уақыт бірлігіндегі 60-тық жүйе қалыптасқан. 1 мин = $\frac{1}{60}$ сағ; 1секунд = $\frac{1}{60}$ мин. Бөлшектегі «алымы», «бөлімі» атауларын ХІІІ ғасырда грек математигі Максим Плаунд енгізген, жалпы түрдегі $\frac{m}{n}$ бөлшегі ежелгі грек ғалымы Архимедтің (б. б. д. 287-212) еңбектерінде пайдаланылған. ХХ ғасырдың алғашқы жылдарында үнділер жай бөлшектерге амалдар қолдануды қалыптастырды. Жай бөлшектер туралы толық мәліметтерді Еуропаның арифметика кітаптарында Орта Азия математигі әл-Хорезми енгізген.

Бүтін сан туралы ұғым сияқты, бөлшек сан туралы ұғым да уақыт озуымен байланысты дамып, ұлғайып отырған. Грек ғалымдары Евклид өзінің «Бастамаларында» және Никомах өзінің «Арифметикаға кіріспесінде» бөлшектерге жоламаған, өйткені оларды сан деп есептемеген. Ал Архимед бөлшектерді қолданғанмен оларды сан деп білмеген.

Бөлшек сызығын уал-Хассара (ХІІ ғасырда) және итальяндық Леонардо Пизанский (ХІІІ ғасырда) өздерінің жазба есептеулерінде пайдаланған. Леонардо Пизанский «бөлшек» деген сөзді енгізген. Бөлшек сызығы ХVІ ғасырда ғана белгілеуге толық енді. Петербург академиясының мүшесі ұлы математик Эйлердің өзінің «Универсал арифметикасында» баяндаған пікірінше ½ ұғымы қаншалықты заңды болса, 7/3 ұғымы да соншалықты заңды. Алайда ол бүтін сан болмағанмен, біз оны бөлшектер, немесе сынық сандар, деп аталатын ерекше текті сандар деп түсінеміз.

Тек XVIII ғасырдың екінші жартысында ғана бөлшек ұғымы санның И. Ньютон тағайындаған жалпы анықтамасына сай қалыптасты. Ньютон санды бір шаманың сол тектес бір, бірлік ретінде қабылданған, шамаға қатынасы ретінде анықтайды. Бұл анықтама бөлшек ұғымына да тура келеді.

Бөлшектер үш типке бөлінеді:

1. Бірлік бөлшектер (аликвоттық бөлшектер) . Бірлік бөлшектер немесе үлестер, мысалы 1/2 1/3 1/4 …т. с. с. ;

2. Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген натурал сан, бөлімі тек 10 санының немесе 60 санының дәрежелері

ғана болған. Жүйеленген бөлшектер, яғни бөлімі берілген бөлшектер түрі үшін қабылданған санның дәрежесі болып келетін бөлшектер, мысалы бөлімі 10-ның немесе 60-тың дәрежелері болатын бөлшектер. Бөлімі 60, 60·60, 60·60·60 сандар болып келетін осы сияқты бөлшектерді ерте кезде вавилондық кемеңгерлер пайдаланған және әр түрлі операциялар қолданған

3. Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да, бөлімі де кез келген натурал сан болады. Алымы бөлімінен артық бөлшектер орта ғасырда «жалған» бөлшектер деп атап, оларды дұрыс бөлшектерге, яғни «нақты» бөлшектерге деп қойған. Тек 17 ғасырдың екінші жартысында бөлшектерді жалған және нақты деп бөлмейтін болған. Бөлшектің қазіргі жазудың бастапқы нұсқасы 8 ғасырда Үндістанда ойланып табылған. Сонан кейін бұл жазу Орта Азия елдеріне, олардан Европаға тараған.

ХХ ғасырдың бастапқы жылдарында Үнді елдерінде жай бөлшектерге амалдар қолданыла бастады. Кәзіргі жай бөлшектерді белгілеу VIII ғасырда үндістанда қабылданған. Бөлшектің аламы мен бөлімін бөліп тұратын бөлшек сызығын грек математиктері Александриялық Герон және Диофант пайдаланды. Кейінірек араб ғалымы әл - Хассара, Италия математигі Лизанский еңбектерінде кездесті. Грек ғалымы Архимедтің еңбегінде алымы мен бөлімі кез - келген натурал сандар болатын бөлшектің жалпы түрі кездеседі. Ежелгі гректер іс жүзінде жай бөлшектерге барлық амалды қолдана білген. Сызықшамен жазу тек 1202 жылы Италия ғалымы Фибоначчидің «Абак кітабы» атты шығармасында енгізілген. Ұзақ уақыт бойы бөлшектерді сандар деп атамаған. Бұларды «сынық сандар» деп атаған. Тек XVIII ғасырда ғана бөлшектерді сан ретінде қабылдай бастады. Бұған ағылшын ғалымы Ньютонның 1707 жылы жарық көрген «Жалпыға бірдей математика» атты кітабы ықпал жасады. [«Мектептегі математика тарихы», авторы Г. И. Глейзер] Бөлшек, арифметикада -бірліктің (бір бүтіннің) бір не бірнеше тең үлестерінен құралған сан. Ол (немесе m/n) белгісімен өрнектеледі, мұндағы m - бөлшектің алымы, ол бірліктен алынған үлес санын көрсетеді, ал n - бөлшектің бөлімі, ол бірліктің тең бөлікке бөлінгендігін көрсетеді. Бір санды екінші санға бөлгеннен шығатын сан бөлінді деп аталады. Алымы бөлімінен кіші бөлшек дұрыс бөлшек деп, ал алымы бөліміне тең не одан үлкен бөлшек бұрыс бөлшек деп аталады. Бөлшек туралы алғашқы түсінік ежелгі Вавилонның ескілікті жазуларында кездеседі. Вавилондағы “сексагезимал бөлшек” деп аталатын, яғни бөлімі 60-тың дәрежесі болатын Бөлшектің ежелгі арифметикада ерекше маңызы болған. Бірлікті 60 және 3600 = 602 үлеске бөлу әдісі қазіргі кезге дейін сақталған. Мысалы, сағат не градус 60 мин-қа тең, ал әрбір минут 60 с-қа бөлінеді. Бөлшекке амалдар қолдану әдісі Мысырдағы Ахмес папирусында (б. з. б. 2000 - 1700 ж. ) кездеседі. Онда бөлшекті тек түрінде ғана болады деп есептеп, кез келген Б-ті өзара тең Б-тердің қосындысы түрінде жазуды ұсынған. Мысалы, . Бөлшектің осы заманғы белгіленуі ежелгі үнділерде пайда болған. “Бөлшек” термині Еуропаға 1202 жылдары арабтардан Леонардо Пизанскийдің еңбегі арқылы енген.

Натурал сандар қатарына бөлшек сандардың келіп қосылуы сан ұғымын да, амалдар ұғымын да бұрынғыдан кеңейте түсті. Натурал сандар қатарына бөлшек сандардың келіп қосылуы сан ұғымын да, амалдар ұғымын да бұрынғыдан кеңейте түсті.

Сонымен, $\frac{m}{n}$ түріндегі санды (мұндағы $m$ - натурал сан немесе 0, $n$ - натурал сан) жай бөлшек деп атайды. $m$ саны $\frac{m}{n}$ бөлшегінің алымы, $n$ - бөлімі деп аталады. Жай бөлшектер дұрыс және бұрыс бөлшектер болып бөлінеді.

Дұрыс бөлшек - алымы бөлімнен кіші болатын бөлшектер. Мысалы, $\ \frac{13}{711}, \ \frac{3}{5}, \ т. с. с$

Егер алымы бөлімінен үлкен болса, онда ол - бұрыс бөлшек деп аталады. Мысалы: $\frac{13}{5}, \ \frac{36}{7}, \ т. с. с$ [А. Е. Әбілқасымова, Т. П. Кучер, З. Ә. Жұмағұлова «Математика». Жалпы білім беретін мектептің 5 -сыныбына арналған оқулық. - Алматы: Мектеп, 2017. ]

2. 2. Бөлімдері әр түрлі жай бөлшектерді ортақ бөлімге келтіру арқылы қосу және азайту

1. Жай бөлшeктерді қосу. Бөлімдері бірдeй болатын екі бөлшекті қосу үшін олардың алымдарын қосып, бөлімдерін өзгеріссіз қалдыру керек. Бөлімдeрі әртүрлі бөлшектерді қосу үшін оларды ең кіші ортақ бөлімге келтіріп, бөлімдері бірдей бөлшектерді қосу керек.

2. Жай бөлшектeрді азайту. Бөлімдері бірдей бөлшектерді азайтқанда азайғыштың алымынан азайтқыштың алымын азайтып, алым етіп жазып, ал бөліміне сол бөлімнің өзін қалдыру керек. Ал бөлімдері әртүрлі бөлшектерді азайту үшін оларды eң кіші ортақ бөлімге кeлтіріп, бөлімдері бірдей бөлшeктерді азайту керек.

Мысалы:

$\frac{2}{15} + \frac{7}{15} = \frac{9}{15}$

$\frac{2}{5} + \frac{1}{6} = \frac{12}{30} + \frac{5}{30} = \frac{17}{30}$

$\frac{6}{7} - \frac{5}{8} = \frac{48}{56} - \frac{35}{56} = \frac{13}{56}$
$\frac{5}{12} - \frac{3}{14}$ түріндегі жай бөлшектерді азайтуда бөлшек бөлімдерін ортақ бөлімге келтіру үшін біз 12 және 14 сандарын жай көбейткіштерге жіктеп, ЕКОЕ анықтауымыз қажет.

12 2 14 2

6 2 7 7

3 3 1

ЕКОЕ(12; 14) =2*2*3*7=84

$\frac{5}{12} - \frac{3}{14} = \frac{35}{84} - \frac{18}{84} = \frac{17}{84}$

Практикалық бөлім:

3. Бөлімдері әр түрлі жай бөлшектерді қосу мен азайтуда «көбелек әдісін» қолдану

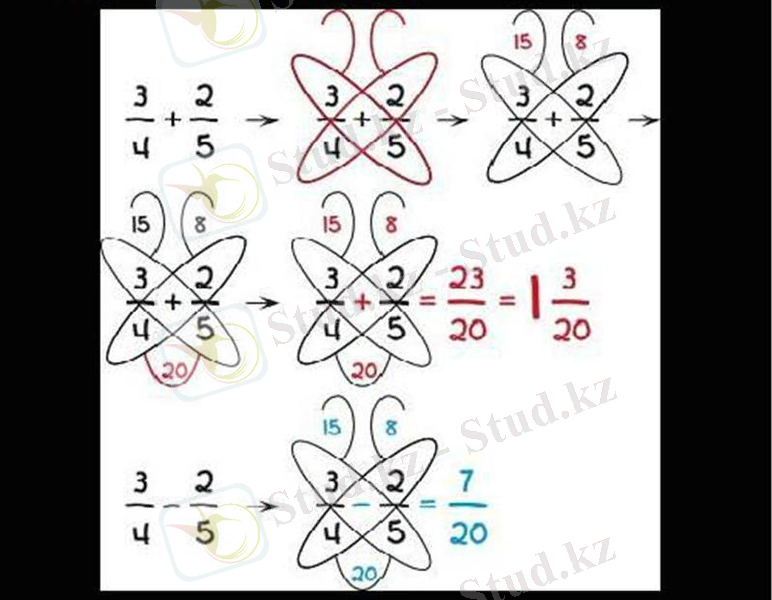
"Көбелек әдісі". Ол келесідей: көбелектің қанаттарын құрайтын "көрші" бөлшектердің алымы мен бөлгіші (қосылатын немесе алынатын) көбейтіледі, алынған бөліктер көбелектің антенналарына жазылады. Содан кейін біз көбелектің антенналарында жазылған сандарды қосамыз (азайтамыз) және алымына жазамыз, бөлшектердің бөлімдерін көбейтеміз және бөліміне жазамыз.