Ламинарлық және турбуленттік қозғалыс кезіндегі жылу алмасу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

ТАҚЫРЫП 10 Ағымды жылу алмасу

Дәріс жоспары:

Ағымды жылу алмасуға әсер ететін факторлар.
Ньютон - Рихман заңы.
Ламинарлық және турбуленттік қозғалыс кезіндегі жылу алмасу.
Ұқсастық теориясынан алынған қысқаша мәліметтер.

1. Ағымды жылу алмасуға әсер ететін факторлар.

Конвективті жылу алмасу дегеніміз - бұл қатты бет пен қоршаған орта арасындағы кез келген жағдайда ламинарлық шекарасыз жүзеге асатын жылу беру процесі, ал қалған жағдайда(көлемде) жылулық тасымалдау конвекциямен жүзеге асады . Конвекцияның екі түрі бар : азатты ( табиғи ) және амалсызды. Азатты конвекцияда сұйықтық амалсыздан сыртқы күштердің ( насос, желдеткіш, жел ) әсерінен қозғалғанда, тығыздыққа байланысты қозғалады. Конвективті жылу алмасудың негізгі теңдуі Ньютон теңдеуімен сәйкес келеді, жылу мөлшері Н бетіне және ∆t температуралар айырымдарына пропорционал :

Q=αH(t ₁ − t ₂ ), (10. 1)

Мұндағы пропорционалдық коэффициенті α  жылу беру коэффициенті(Вт/(м ² ⋅К) ), бір градусқа градиентте бірлікпен берілетін салыстырмалы жылу ағынынының мөлшері. Жылу беру коэффициенті былай көрсетуге болады:

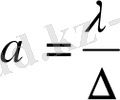(10. 2)

Мұндағы ∆ - ламинарлық шекара қабатының жуандығы .

Бұдан біз α-ның аналогтық ∆ факторына көп тәуелді екенін және аналитикалық шешімі жоқ екенін көреміз. Жылу берілу коэффициентін анықтау тәжірибеде іске асады және бұл конвективті жылу алмасудың эмпиризмдік екенін дәлелдейді . Тәжірибедегі теорияны қолдану және мөлшерлілік теориялары тәжірибелік мәліметтерді жалпылауға мүмкіндік туғызады және конвективті жылу алмасу гидродинамикалық және жылу параметрлеріне тәуелділігінен полуэмпиритикалық мінезге ие болады.

2. Ньютон - Рихман заңы.

Мөлшерлілік теориясы дифференциалдық теңдеу жоқ болған кезде, яғни қазіргі процесті сипаттау қолданылады. Амалсыз конвекция шарттарында жылу беру коэффициентінің мәні кем дегенде алты тәуелсіз айнымалының функциясы бола алады: салмақ жылдамдығы u, кг/(м ² ⋅с) ; ұзындық мөлшері l ; тұтқырлық

μ, кг/(м⋅с) ; жылусыйымдылық С, Дж/(кг⋅К) және тығыздық ρ, кг/м ³ , жылуөткізгіштік λ, Вт/(м⋅К) .

Тәжірибеде анықталғандай α -ның Вт/(м ² ⋅К) бағыныштылығын α-дан бастап 6 ауыспалы және сандарды (мұндағы А=10) тәжірибеден өткізу керек, мысалға А = 10; n - бағынбайтын ауыспалы сандар. Бұдан тәжірибелер саны бір миллионға тең екенін көреміз, бұл нақты сан болмайды. Мөлшерлілік теорияларды қолдану тәуелсәз ауыспалыларды қысқартуға мүмкіндік береді . Амалсыз конвекция шарттарында жылу беру коэффициенті функция болып келеді

α = α(u, l , μ, С, ρ, λ) . (10. 3)

Толық дифференциал α мынаған тең:

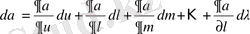. . (10. 4)

Келесі өлшемсіздерге ( салыстырмалымен ) өту үшін тұрақты о-ден басқа өзгергіш мөлшерлер қажетті болады. Aлынған теңдеуді α-ға бөлеміз және бір уақытта сәйкес белгілерге ( l / l ; u/u; μ/μ т. с. с ) бөлеміз және көбейтеміз, сонда

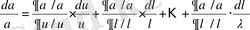. . (10. 5)

Жеке туынды арақатынастарын тұрақты деп есептейміз :

; ; …; ,

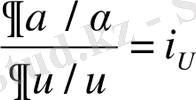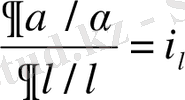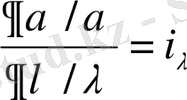Сонда мынаны аламыз

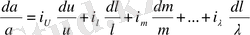. . (10. 6)

Алынғанды интегралдаймыз :

ln α=i _u ln u+i _l ln l +…+i _λ ln λ+ln C ₀ (10. 7)

Потенциалдасақ, мынаны аламыз

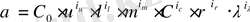. . (10. 8)

Қажетті шартпен алынған жалпы шешім тұрақты С ₀ немесе оның кері мөлшері болуы керек :

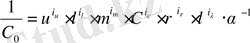. . (10. 9)

Бұл теңдеу бірліктер жүйесіне тәуелді болмайды, ал С ₀ өлшемсіз болғандықтан, барлық өлшеулердің бірліктері ( оңңан ) «0» дәрежеге теңдеуге кіреді, яғни мөлшерліліктің жоғына байланысты

3. Ламинарлық және турбуленттік қозғалыс кезіндегі жылу алмасу.

Жылу берудің тегіс құбырларда күшейе түсуі ағын тәртібіне байланысты, мына мөлшермен анықталады Re=ωd/ν. Егер Re≤Re _кр болса, онда ағын тәртібі ламинарлық . Сұйық құбыр бойымен қозғалғандағы формула: Re _кр =2⋅10 ³ . Турбулентті ағын Re>10 ⁴ , ал Re=2⋅10 ³ ÷1⋅10 ⁴ ауыспалы тәртіпке сәйкес келеді. ағым дамыған турбулентті тәртібі орналастырады . Мұндағы Re - Рейнольдс критерийі тұтқырлық күші мен инерция күшінің қатнасын сипаттайтын сұйық қозғалысы гидродинамикалық ұқсастық тәртібі параметрі.

Ламинарлық қозғалыс құбыр қимасында және ағымдағы сұйықтың тығыздығының өзгеруі кезінде температура әжептәуір өзгеріске ұшырайды. Содан кейін жылу тасушы амалсыз қозғалыс еркін қозғалысқа айналады. Грасгоф интенсивті еркін қозғалысты сипаттайды. Құбырдағы сұйықтық амалсыз ламинарлық жылу беру қозғалысы кезінде құбырдың орташа ұзындығы коэффициенті, еркін қозғалысты ескере отырып Nu критерийімен анықталады:

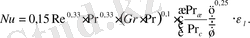(10. 10)

Академик М. А. Михеев ұсынған теңдеу (10. 10) Re<2000 жағдайында құбырларда және каналдарда жылу беруді бағалау үшін және жабысқақ гравитациялық тәртібінде қолданылады. Бұл теңдеуде құбырлардағы және әртүрлі көлденең қима каналдарындағы орта жылу беруді анықтайды . Оны анықтау үшін құбырлардың диаметрі немесе каналдың эквиваленттік диаметрі керек:

d _э =4F/P, (10. 11)

Мұндағы P - канал периметрі :

F - көлденең қиманың ауданы .

Коэффициент ε _l формулада (10. 11) l /d тәуелді болады мұндағы l ― құбыр ұзындығы . l /d>50, ε _l =1 қысқа құбырларда l /d тәуелділігінді :

Кесте 4. 4

ε _l коэффициенті мәні

1: 1

2: 2

5: 5

10: 10

15: 15

20: 20

30: 30

40: 40

50: 50

: ε _l

1: 1, 9

2: 1, 7

5: 1, 44

10: 1, 28

15: 1, 18

20: 1, 13

30: 1, 05

40: 1, 02

50: 1

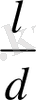
Турбулентті тәртіпті ағын кезінде сұйықтықтың өте қарқынды араласады және табиғи конвекция интенсивті жылу алмасуға әсер етпейді. Орташа ұзындықты құбырға арналған жылу беру коэффициент дамыған турбулентті қозғалыс кезінде (Re≥10 ⁴ ) академик М. А. Михеев келесі теңдеуді пайдалануға ұсынды :

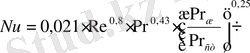(10. 12)

(10. 12) теңдеуге Грасгоф критерийі кірмейді, себебі еркін қозғалыс жылу беру қозғалысына ықпалын етеді . Теңдеу (10. 12) әр түрлі көлденең қималы құбырға, оның ішінде айналмалы (d ₂ /d ₁ =1÷5, 6) және сызаттықты (а/b=1÷40) қозғалыс үшін берілген.

(10. 11) және 10. 12) Теңдеулерде температураны анықтау үшін сұйықтықтар ағынындағы орташа температура қабылданған. Құбыр диаметрінің немесе кез келген құбырдың эквиваленттік диаметрі - анықтаушы геометриялық мөлшер.

Ауаға арналған формула (10. 12) оңайланады :

Nu=0, 018⋅Re ^{0, 8} . (10. 13)

Ауыспалы ағын кезінде жылу беру бірыңғай ұқсаулар теңдеумен суреттелмейді, бұндай шарттарда сандық мәні қиын берілген қозғалыс пен жылу алмасу көптеген факторларға тәуелді болады. Re=idem кезінде жылу берудің максимальді коэффициенті 20÷100 болады. Сондықтан жылу айырбас тәртіптерінің мына облысына арналған сондықтан жылу беру коэффициенттерінің мүмкіндігіне байланысты анықтайды.

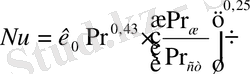(10. 14)

к ₀ мөлшер белгісі Re критерийі тәуелділігінде шығады

Кесте

к ₀ мөлшерінің мағынасы

Re⋅10−3: Re⋅10 ⁻³

2, 2: 2, 2

2, 3: 2, 3

2, 5: 2, 5

3, 0: 3, 0

3, 5: 3, 5

4: 4

5: 5

6: 6

7: 7

8: 8

9: 9

10: 10

Re⋅10−3: к ₀

2, 2: 2, 2

2, 3: 3, 6

2, 5: 4, 9

3, 0: 7, 5

3, 5: 10

4: 12, 2

5: 16, 5

6: 20

7: 24

8: 27

9: 30

10: 33

4. Ұқсастық теориясынан алынған қысқаша мәліметтер

Ұқсау теорияларын қолданғанда өтіп жатқан процесті зерттеу үшін дифференциалды теңдеу болу керек. Бұл теңдеуді критериялық өңдеуден өткізсек, критерийдің ұқсау белгілерінің құрамын аламыз. Критерийдің ұқсау белгілерінің құрамы «губки » әдісімен жүзеге асырылады: негізгі дифференциалды теңдеуде дифференциялдардың белгілері түседі, алынған нәтижелер теңестіріледі, ұқсау параметрлерін анықтайтын тәуелсіз қосылғандар ерекшеленеді.

Конвективті жылу алмасу үшін ( оның математикалық суреттеуі ) : 1) Навье - Стокстың сығылмайтын сұйықтың қозғалыс дифференциалды теңдеуі; 2) Фурье - Кирхгофтың жылу өткізгіштік теңдеуі; 3) Био - Фурьенің қоршаған ортадағы қатты беттің үстіңгі шекарасындағы жылу алмасу теңдеуі болуы керек.

Сығылмайтын сұйықтық қозғалыс теңдеуі :

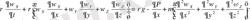(а)

Ұқсау теорияның «губки» әдісі негізінде 5 тәуелсіз кешенді аламыз ( теңдеу бір өлшемді « Х » осі үшін жазылған) .

№ п/п: № п/п

1: 1

2: 2

3: 3

4: 4

5: 5

№ п/п: кешендер

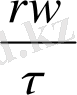
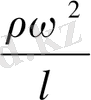
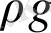
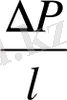
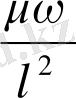
Алынған тәуелсіз кешендерді топтаймыз және критерий белгілері аламыз :

2:1 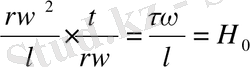; (10. 15)

2:5 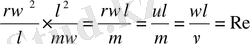; (10. 16)

4:2 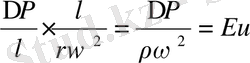; (10. 17)

3:2 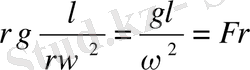, (10. 18)

Деп бөлеміз. Мұндағы Но - гомохрондық критерий, яғни оқиғалардың бір мезгілділк гидродинамикалық белгісі ;

Re - Рейнольдс критерийі, сұйық қозғалысының гидродинамикалық параметрі селқостық күштерінің арақатынасына және жабысқақтық күштерге мінездемі береді;

Eu - Эйлер критерийі, селқостық күштерінің және қысым күштерінің арақатынасын сипаттайды ;

Fr - Фруд критерийі, селқостық күштерінің және ауырлық күштерінің арақатынасын сипаттайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.