Бастауыш сыныптарда үлес ұғымдарын оқытудың әдістемесі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Үлес тақырыбы бастауыш сыныптарда оқыту әдістемес

МАЗМҰНЫ
КІРІСПЕ3
І Бөлім Үлес және бөлшек ұғымдарының теориялық негіздері6
1.1. Үлес және бөлшек ұғымдары туралы түсінік6
1.2.Бастауыш сынып математикасында үлес және бөлшек ұғымын кеңейтіп оқытудың маңызы10
ІІ Бөлім Бастауыш сыныптарда үлес ұғымдарын оқытудың әдістемесі14
2.1. Бастауыш сыныпта санның үлесін және үлесі бойынша санды14
табуды үйретудің ерекшеліктері14
2.2 Бастауыш мектепте үлес ұғымын оқыту әдістері18
III.Бөлім
2.3.ҚМЖ- "Үлес тақырыбы бойынша бастауыш сыныптарда оқыту әдістемесі"
2.4.Практикалық бөлімі
ҚОРЫТЫНДЫ23
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР25

КІРІСПЕ
Курстық жұмыстың өзектілігі: Қазақстан демократиялық жолға түскен өтпелі кезеңінде барлық әлеуметтік-экономикалық түбірмен өзгеруі білім саласының қайта құруына қажеттілік туғызды. Бұл орайда жүргізіліп жатқан реформалар бұрынғы қол жеткізген жетістіктерді сақтай отырып, білім беру жүйесін ары қарай дамыту жолдарын белгілеу қажет болды. Алайда егемендіктің алғашқы жылдары бұрынғы жүйенің тамаша жетістігі болып саналатын міндетті өзгеріске ұшырап батысқа көшуге талпыныс жасалды. Ендігі жерде білім беру саласында әлемнің алдыңғы қатарлы елдердің тәжірибесіне сүйеніп, жаңа мемелекеттің даму барысын ескере отырып, жинақталған тәжірибеге арнайы талдау жасау қажет.
Адамзаттың бөлшек сандар туралы түсінігі ерте замандарда - ақ қалыптасқан, сондықтан бөлшек ұғымының пайда болу процесін өте дәл сипаттау мүмкін емес. Бөлшек сандар әр түрлі шамаларды - ұзындықты, массаны, ауданды және т.с.с. өлшеу процесіне байланысты пайда болуы ықтимал. Барлық халықтарда теңдеу бөлуге байланысты бөлімі екіге тең болатын бөлшектер ерекше орын алған.
Бастауыш сыныпта үлес, бөлшек, оларды жазу, салыстыру, санның үлесін, үлесі бойынша санды табу, санның бөлшегін табу сияқты мәселелер қарастырылады. Балаларды үлестермен танысыру практикалық іс-әрекет арқылы жүзеге асырылады. Бөлшек туралы алғашқы түсінік нақты заттар геометриялық фигуралар, шамаларға пркактикалық амалдар қолдану арқылы беріледі.
Курстық жұмыстың мақсаты: бастауыш сынып оқушыларына үлес және бөлшек ұғымдарын оқыту.
Курстық жұмыстың зерттеу объектісі: оқушыларға үлес пен бөлшек қасиеттерін қалыптастыру мәселелері.
Курстық жұмыстың зерттеу пәні: оқушыларға үлес және бөлшек ұғымдарын қалыптастырудың тиімді жолдарын анықтау.
Курстық жұмыстың міндеттері:
- Үлес және бөлшек ұғымдары туралы түсінік қалыптастыру;
- Бастауыш сынып математикасында үлес және бөлшек ұғымдарын кеңейтіп оқытудың маңызын сипаттау ;
- Бастауыш сыныпта санның үлесін және үлесі бойынша санды табуды үйретудің ерекшеліктерін көрсету;
- Рационал бөлшектер және олардың қасиеттерін оқытудың жолдарын анықтау;
- Оң рационал сандарды ондық бөлшек түрінде жазуды үйретудің әдіс-тәсілдеріне тоқталу.
Зерттеу көздері: Зерттеу мәселесі бойынша математика, педагогика ғалымдардың, әлеуметтанушылардың, психологтардың еңбектері; ҚР Білім беру туралы Заңы; Елбасшысының халыққа жолдаған Қазақстан - 2030 үндеуі; Кәусар бұлақ бағдарламасы; Атамекен бағдарламасы; Қазақстан Республикасында жалпы орта білім беру тұжырымдамасы; ҚР 2015 жылға дейінгі білім беруді дамыту тұжырымдамасының педагогикалық және жас ерекшелігі психологиясы теориялары, ұлттық тәлім-тәрбие туралы ғылыми зерттеулер мен теориялық әдебиеттері негіздеріне сүйеніп жасалған.
Курстық жұмыстың құрылымы: курстық жұмыс кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспе бөлімінде осы тақырыптың көкейкестілігі, бастауыш мектепте математикалық үлес және бөлшек ұғымдарын үйрету мәселелері және оқу-тәрбие процесінің бірізділігі, оны зерттеуге ат салысқан ғалымдардың еңбектерінің құндылығы қарастырылды. Зерттеу жұмысының ғылыми аппараты, мақсаты, міндеттері әдістері объектісі мен пәні көрсетілді.
Үлес және бөлшек ұғымдарының теориялық негіздері деп аталатын бөлімде үлес және бөлшек ұғымдары туралы түсінік қалыптастыру және бастауыш сынып математикасында үлес және бөлшек ұғымдарын кеңейтіп оқытудың маңызы қарастырылады.
Бастауыш сыныптарда үлес және бөлшек ұғымдарын оқытудың әдістемесі деп аталатын бөлімде бастауыш сыныпта санның үлесін және үлесі бойынша санды табуды үйретудің ерекшеліктері мен рационал бөлшектер және олардың қасиеттерін оқытудың жолдары және оң рационал сандарды ондық бөлшек түрінде жазуды үйретудің әдіс-тәсілдері қарастырылады.

І Бөлім Үлес және бөлшек ұғымдарының теориялық негіздері
1.1. Үлес және бөлшек ұғымдары туралы түсінік

Адамзаттың бөлшек сандар туралы түсінігі ерте замандарда - ақ қалыптасқан, сондықтан бөлшек ұғымының пайда болу процесін өте дәл сипаттау мүмкін емес. Бөлшек сандар әр түрлі шамаларды - ұзындықты, массаны, ауданды және т.с.с. өлшеу процесіне байланысты пайда болуы ықтимал. Барлық халықтарда теңдеу бөлуге байланысты бөлімі екіге тең болатын бөлшектер ерекше орын алған.
Біздің заманымызға дейін жеткен ежелгі вавилон жазбаларында алпыстық бөлшектердің қолданылғаны туралы мәліметтер кездеседі. Ежелгі мысыр папирустарынан Мысыр елінде алымы 1-ге тең бөлшектер қолданылғаны белгілі.
Сондай-ақ, Грецияда да алымы 1-ге тең болатын бөлшектер қарастырылған. Үнділер мен арабтар бөлшекті оның алымын бөлімінің үстіне (бірақ бөлшек сызығынсыз) орналастыру арқылы жазған. Үнділер енгізген позициялық санау жүйесі бөлшектерге қолданылмаған.
Бөлшек санды жазып көрсетуде бөлшек сызығын пайдалану Леонарда Пизонскийдің (ХІІІ ғасыр) еңбектерінде кездеседі. Алайда, бөлшекті бөлшек сызығы арқылы жазып көрсету ХҮІ ғасырдан бастап қана жаппай қолданыла бастады.
Самарқанд қаласындағы астрономиялық обсерваторияның негізін салушы Әл - Кәши бөлшек сандарды жазудың, барлық түрлендірулер мен есептеулерді айтарлықтай ықшамдайтын түрін, яғни ондық бөлшектер деп аталатын жаңа түрін ашқан. Бұл жаңалықтарын ол 1427 жылы Санау өнерінің кілті деп аталатын еңбегінде баяндаған.
Дәл осы жаңалықты, Әл-Кәшиден жүз елу жылдан астам кейініріек, Европада Нидерланд ғалымы Симон Стевин ашты. Ол мұны 1585 жылы Ондық санау жайында атты еңбегінде баяндады.
ХҮІІ ғасырдың басында ондық бөлшектерді жазуда айыру таңбасы ретінде, үтір немесе нүкте қолданыла бастады. Өзінің еңбектерінде ондық бөлшектер теориясын баяндаған. Дж. Непер (1550-1617) де осындай белгілеуді ұсынған. Ондық бөлшектерді белгілеудегі ең бір қолайлы таңбасы Австрия астрономы Иоганн Кеплер (1517-1630) ұсынған бірліктер разряды мен ондық үлестер разряды арасын үтір арқылы айыру болып табылады.
Европада көп уақыт бойына, тек ХҮІІІ ғасырда бөлшектер ығыстырып шығарған алпыстық бөлшектер қолданылып келді.
Россияда ондық бөлшектер жайындағы алғашқы жүйелі мәліметтер Магницкийдің Арифметикасында (1703ж.) кездеседі.
Ондық бөлшектер Француз буржуазиялық революциясынан кейін 1789 жылы өлшем және салмақ бірліктерінің ондық жүйесінің енгізілуімен байланысты математикада толығынан орын тапты.
Үнді, Таяу және Орта Шығыс математиктері алгебраны, тригонометрияны және астрономияны дамыту барысында иррационал шамалармен амалдай тұрғаны түсінікті. Бірақта олар көп уақыт бойына иррационал шамаларды сан ретінде қарастырмаған.
ХҮ ғасырда Арифметиканың кілті атты еңбегінде Әл-Кәши ондық бөлшектерді енгізді және оны түбір табудың дәлдігін жетілдіруде қолданды. Европада оған байланыссыз тура осы жолмен Симон Стевин 1585 жылы ондық бөлшектерді ашты. Ол өзінің Алгебраға қосымшалар (1594) атты еңбегінде ондық бөлшектерді нақты санға шексіз жақын жуықтауларда қолдануға болатындығын көрсетті.
Сонымен, ХҮІ ғасырда онлық бөлшектер иррационал сан ұғымын енгізу және оны негіздеудің табиғи құралы болып табылады деген пікір туындады.
ХҮ ғасырдан бастап және ХҮІ ғасырда алгебралық теңдеулерге деген қызығушылықтың артуына байланысты математиктер сандардан түбір табу сияқты амалдар қолдану арқылы алынатын өрнектермен жиі істес бола бастады. Ал мұндай өрнектердің мәні рационал сандар бола алмайтындығы түсінікті еді. Бұл шаманың нені сипаттайтындығы жөніндегі айқын түсініктері қалыптаспағанымен, математиктер оларға үйреншікті жалпы ережелерге негізделген амалдарды қолданды. Шын мәнісінде, мұның өзі ( айқын болмаса да) иррационал сандардың негізіле бастауын көрсетеді.
Декарттың Геометриясының жақрықа шығуы кез келген кесінділерді (жалпы алғанда геометриялық шамаларды да) өлшеу мен рационал сан ұғымын кеңейту қажеттілігі арасындағы байланысты түсінуді жеңілдетті. Мәселе иррационал сандарды рационал сандар сияқты сан осінде нүктелер арқылы кескіндеуге болатындығында еді. Ирационал сандардың бұл геометриялық мағынасы олардың табиғатын түсінуге және оларды мойындауға игі әсер етті.
Координаталық жүйені енгізу (ХҮІІ ғ.) арқылы сандар мен нүктелер арасындағы байланыстың игілікті және терең негізде тағайындалуы тек жекеленген иррационал өрнектерді (сандарды) ғана емес, сонымен бірге наты сандардың барлық жүйесін қарастыруды қажет етті. Сонымен, ХІХ ғасырда нақты сандардың қасиеттерін және олардың толық теориясын негіздеу жүзеге асырылады.
Осыған сәйкес анықтамалар мен ой қорытындылардың толық жүйесін құруды ХІХ ғасырдығ екінші жартысында неміс математигі Дедекинд (1831-1916) Үздіксіз және иррационал сандар (1872ж.) атты еңбегінде іске асырды. Бұл еңбек небары 21 парақтан тұрады, алайда ол математика тарихына осы ғылымның классикалық туындыларының бірі ретінде енді.
Мұнымен бір уақытта кейбір математиктер (Мере, Кантор, Вейерштрасс) нақты сандарды басқа көзқарас тұрғысынан негіздеуді жүзеге асырды. Олардың әрқайсысы басқа бір ұғымдарға сүйене отырып, шын мәнінсінде Дедекинд теориясына эквивалентті болатындай теорияны құрғандығын ескертуге тиіспіз.
Иррационал сандар - рационал бола алмайтын нақты сандар.
Иррационал сан ұғымы түбір табу, кесіндінің ұзындығын өлшеу мен кейбір функцияларды зерттеу барысында пайда болды. Иррационал сандардың І жиыны Q рационал сандар жиынының нақты сандардың R жиынына дейінгі толықтауыш жиыны болып табылады. Иррационал сандарды Дедекинд қимасы немесе шексіз периодты емес, ондық бөлшек арқылы анықтауға болады.

1.2.Бастауыш сынып математикасында үлес және бөлшек ұғымын кеңейтіп оқытудың маңызы

Бөлшектердің пайда болуы шамаларды өлшеумен байланысты. Мысалы ретінде, кесіндінің ұзындығын өлшеу кезінде бөлшектердің қалай пайда болатындығын қарастырайық.
а кесіндісін алайық. Оның ұзындығын табу үшін, ұзындық бірлігі ретінде е кесіндісін таңдап аламыз. Өлшеу кезінде а кесіндісінің ұзындығы 3е - ден артық, бірақ 4е-ден кем болып шықты. Сондықтан оның ұзындығын натурал санмен өрнектей аламаыз (е ұзындық бірлігінде). Бірақ е кесіндісін әрқайсысы е1-ге тең 4 бөлікке бөлсек, онда а кесіндісінің ұзындығы 14е1 - ге тең болып шығады. Егер ұзындықтың бастапқы бірлігі е-ге қайтып оралсақ, онда а кесіндісінің ұзындығы туралы біз а кесіндісі е кесіндісінің төрттен бір бөлігіне тең 14 кесіндіден құралған деп айта аламыз, яғни а кесіндісінің ұзындығын екі натурал санмен 14 және 4-пен өрнектеуге мәжбүр боламыз.
Бұл жағдайда кесіндінің ұзындығын е түрінде жазу келісілген, ал 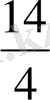жазуын бөлшек деп атайды.
Анықтама. Айталық а кесіндісі мен е бірлік кесіндісі берілсін және де е кесіндісі әрқайсысының ұзындығы е1 болатын n кесінділерінің қосындысы болсын делік. Егер а кесіндісі әрқайсысының ұзындығы е1 болатын m кесінділерден тұратын болса, онда оның ұзындығы түрінде өрнектеледі. символын бөлшек деп атайды, мұндағы m мен n натурал сандар, жазуын эннан эм деп оқиды.
Суретке қайып оралайық. Таңдап алынған е1 кесіндісі е кесіндісінің төрттен бір бөлігі. Бұл а кесіндісінің бойына бүтін сан рет салуға болатын е кесіндісін бөлктеудің жалғыз ғана жолы емес.
Сондай-ақ , е кесіндісінің ұзындығы осындай 28 бөліктен тұрады, ал оның ұзындығы 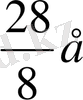-ге тең болады.
Сол сияқты е кесіндісінің 16-дан бір бөлігін де алуғак юолады. Бұл жағдайда а кесіндісі осындай 56 бөліктен тұрады және оның ұзындығы 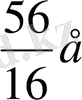-ге тең болады.
Егер осы процесті шексіз жалғастыратын болсақ, онда а кесәндісінің ұзындығы: 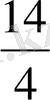; ; 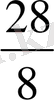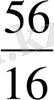,... түріндегі бөлшектердің шексіз жиынымен өрнектелген болар еді.
Жалпы түрде, егер а кесіндісінің ұзындығы е ұзындық бірлігінде бөлшегімен өрнектелген болса, онда оның ұзындығын кез келген 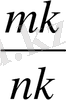, мұндағы k натурал сан бөлшекпен де өрнектеуге болады.
Анықтама. Берілген е ұзындық бірлігінде бір ғана кесіндінің ұзындығын өрнектейтін бөлшектер тең бөлшектер деп аталады.
Егер және бөлшектері тең болса, онда оны былай жазады: =
Мысалы, 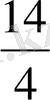және 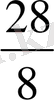бөлшектері е ұзындық бірлігінде бір ғана а кесіндісінің ұзындығын өренктейді. Ендеше, олар тең бөлшектер , яғни
=
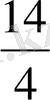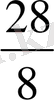
Бөлшектердің тең екендігін анықтау үшін мынадай белгіні қолданады: және бөлшектерді тең болу үшін m q = n p теңдігі орындалуы қажетті және жеткілікті.
1. = m q = n p болатындығын көрсетейік. Кез келген натурал q үшін =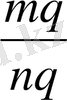, ал кез келген натурал сан n үшін = 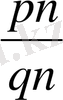болғандықтан,
және бөлшектерінің теңдігінен 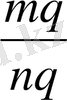= 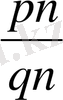шығады.
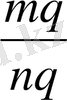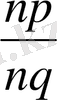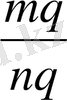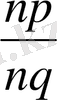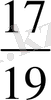2. m q = n p = болатындығын көрсетйік. Егер mq=np тура теңдігінің екі жағында nq натурал санына бөлсек, онда = түріндегі тура теңдік аламыз. Бірақ =, ал = . Мысалы: және 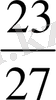бөлшектерінің тең немесе тең емес екендігін анықтайық. Ол үшін 17·27 және 19·23 көбейтінділерін салыстырамыз: 17·27 =459, 19·23=437, 459 437, онда ; .
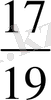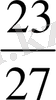Жоғарыда қарастырылған фактілерден бөлшектің негізгі қасиеті шығады:
Егер бөлшектің алымын да, бөлімін де бірдей натурал са,ға көбейтсек немесе бөлсек, онда берілген бөлшекке тең бөлшек шығады.
Бөлшектерді қысқарту және бөлшектерді ортақ бөлімге келтіру осы қасиетке негізделген.
Егер бөлшектің алымы да, бөлімі де бір мезгілде 1-ден басқа санға бөлінбесе, онда мұндай бөлшектерді қысқартылмайтын бөлшектер деп атайды.
Бөлшектерді қысқарту дегеніміз - берілген бөлшекті алымы мен бөлімі берілген бөлшекке қарағанда кем болатындай етіп өзіне тең қысқартылмайтын бөлшектен ауыстыру.
Мысалы: 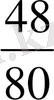бөлшегін қысқартайық. Осы бөлшекке тең, қысқартылмайтын бөлшек алу үшін, бөлшектің алымын да, бөлімін де осы сандардың ең үлкен ортақ бөлгішіне бөлу керек. ЕҮОБ-ті табамыз: Б(80;48) =16.
Бөлшектің алымын да, бөлімін де 16-ға бөліп аламыз: 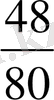=. Алынған бөлшек - қысқартылмайтын бөлшек. Бөлшекті ортақ бөлігіне келтіру дегеніміз - оларды бөлімдері бірдей болатындай тең бөлшектермен ауыстыру.
Және бөлшектің ортақ бөлімі деп n мен q сандарының ең кіші ортақ еселігін айтады.
Мысалы: 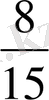және 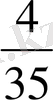бөлшектерін ортақ бөлімге келтірейік. Сонда олардың ортақ бөлімі 15 және 35 сандарының ортақ еселіктері болып табылады. 15 және 35 сандарын жай көбейткіштерге жіктейміз. 15 = 3·5,
35 =5·7. Сонда К( 15,35) = 3·5·7 = 105, ал 105 = 15·7=35·3, болғандықтан, = .

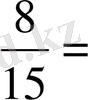
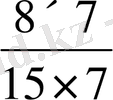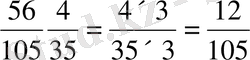ІІ Бөлім Бастауыш сыныптарда үлес ұғымдарын оқытудың әдістемесі
2.1. Бастауыш сыныпта санның үлесін және үлесі бойынша санды
табуды үйретудің ерекшеліктері

Бастауыш сыныпта үлес, бөлшек, оларды жазу, салыстыру, санның үлесін, үлесі бойынша санды табу, санның бөлшегін табу сияқты мәселелер қарастырылады.
Балаларды үлестермен таныстыру практикалық іс-әрекет арқылы жүзеге асырылады. Бөлшек туралы алғашқы түсінік нақты заттар геометриялық фигуралар , шамаларға пркактикалық амалдар қолдану арқылы беріледі.
Жолақтың ұзындығы 12 см, ол 3 тең бөлікке бөлінген. Бір бөлігінің ұзындығы неше сантиметр? (4см)
Қалай білдіңдер?
123 = 4 (см), сонда саны бойынша үлесін табу үшін қандай амал қолданамыз? (бөлу).
Жолақ тең 4 бөлікке бөлінген. Оның бір бөлігінің ұзындығы 3 см. Тұтас жолақтың ұзындығы қанша сантиметр? (12см) Қалай білдіңдер?
4·3 = 12 (см) сонда үлесі бойынша санын табу үшін қандай амал қолданамыз? (көбейту).
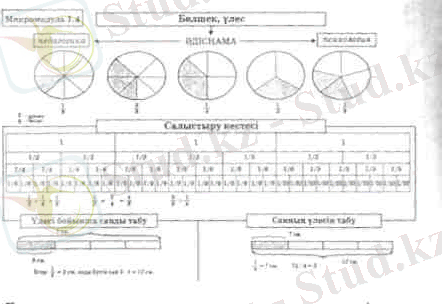
Бөлік, үлес туралы түсінік фигураларды тең бөлікке бөлу, бөлігін табу арқылы қалыптастырылады. Мысалы, геометриялық фигураларды бөліктерге бөлу арқылы үлес ұғымын таныстыру. Слайд бойынша салыстыру кестесін талдап, есеп құрастыр.
Үлесті алғашқы рет көбейту мен бөлуді оқытумен байланысты 3-сыныпта оқытады. Үлесті оқыту шаманы оқытумен тығыз байланысты, сондықтан оқушылар математиканың өмірмен байланысын аңғарады. Оны бүтінді бөліктерге бөлуге проблемалық жағдай туғызудан бастауға болады: Алманы ағасы мен қарындасына ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.