Қозғалыс есептерін шешуді үйретудің әдістемелік ерекшеліктері

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

Мазмұны

Кіріспе
3
1 Бастауыш мектеп математикасындағы қозғалысқа байланысты есептермен жұмыстың теориялық негіздері
5
2 Қозғалыс бойынша мәтіндік есептерді шешуге саналы көзқарастың мәні және оны кіші жастағы оқушыларда қалыптастыру қажеттілігі
5
3 Бастауыш сыныпта қозғалысқа байланысты есептердің түрлері
7
4 Қозғалыс есептерін шешуді үйретудің әдістемелік ерекшеліктері
12
5 Mектеп математикасындағы қозғалысқа байланысты есептермен эксперименттік жұмыс
15

Қорытынды
28
Пайдаланылған әдебиеттер тізімі
29

Кіріспе

Зерттеу өзектілігі. Қазіргі жалпы білім беру жүйесінде математика орталық орындардың бірін алады, бұл, әрине, осы білім саласының бірегейлігі туралы айтады. Бүгінгі таңда математика қазіргі адамзат білімінің өмірлік маңызды салаларының бірі болып табылады және өркениетті қоғамда адамның өмір сүруінің қажеттілігі ретінде қарастырылады.
Қазіргі кезде математиканы оқытуда ерекше орын алатын қимыл-қозғалысқа байланысты есептерді шешуде оқушылардың дербестігін дамыту қажет.
Қозғалыс есептері - әртүрлі (бағытқа және қарама-қарсы бағытта) немесе бір бағытта (кейін және артта) қозғалған екі немесе одан да көп денелердің бір-біріне қатысты қозғалыс процесін сипаттайтын есептің ерекше түрі. Олар өзара байланысты шамаларды қамтиды: жүріп өткен қашықтық, жылдамдық және уақыт.
Қозғалыстағы математикалық есеп оқушыға дұрыс математикалық түсініктерді қалыптастыруға, қоршаған өмірдегі қарым-қатынастардың әртүрлі аспектілерін толық түсінуге көмектеседі, сонымен қатар зерттелетін теориялық түсініктерді пайдалануға мүмкіндік береді. Есептерді шешу балаларда бағдарламамен анықталған толық білімнің қалыптасуына ықпал етеді. Қозғалыс есептерін шешу арқылы оқушылар тек танымдық ғана емес, тәрбиелік мәні бар фактілермен де танысады.
Зерттеу нысаны: бастауыш мектепте математиканы оқыту процесі.
Зерттеу пәні: бастауыш сыныптың мектеп математика курсында оқушыларды қозғалыс есептерінің әртүрлі түрлерін шығаруға үйретудің әдістемелік ерекшеліктері.
Зерттеу мақсаты: бастауыш мектепте математиканы оқыту кезінде оқушыларды қозғалыс есептерін шығаруға үйретудің әдістемелік ерекшеліктерін анықтау және зерттелетін тақырып бойынша оқу-әдістемелік кешендерін әзірлеу.
Зерттеу міндеттері:
қимыл-қозғалыс тапсырмасымен жұмыс жасау сабағында ұйымдастыру мәселесі бойынша әдістемелік әдебиеттерді зерделеу және талдау;
бастауыш сыныпта қозғалыс мәселелерімен жұмыс істеу ерекшеліктерін ашу;
бастауыш мектеп математикасындағы қозғалысқа байланысты есептермен эксперименттік жұмыс жүргізу.
Зерттеу болжамы қимыл-қозғалыс есептерін шешуге үйрету процесінде даралау және саралау принциптерін ескере отырып, жалпылама шешу әдісін қалыптастыру үшін жаттығулар жүйесін қолдану қажет.
Бұл жұмыста келесі зерттеу әдістері қолданылды:
әдістемелік және психологиялық-педагогикалық әдебиеттерді зерделеу және талдау;
педагогикалық жұмыстағы озық тәжірибелерді талдау және жалпылау;
бастауыш сыныптағы математика сабақтарын бақылау және талдау.
Жұмыстың практикалық маңыздылығы оның бастауыш сынып оқушыларына қозғалыс есептерінің негізгі түрлерін шешуге үйретуге арналған тапсырмалар жүйесі мен оларды математика пәнінің мұғалімдері мен студенттеріне педагогикалық практика кезінде қолдануға болатын әдістемелік ұсыныстар беруінде.
Құрылымы. Курстық жұмыс кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

Бастауыш мектеп математикасындағы қозғалысқа байланысты есептермен жұмыстың теориялық негіздері
Қозғалыс бойынша мәтіндік есептерді шешуге саналы көзқарастың мәні және оны кіші жастағы оқушыларда қалыптастыру қажеттілігі

Кіші мектеп оқушыларын оқытудағы басты мақсаттардың бірі - оларда есептерді шешуге саналы көзқарасты қалыптастыру [1].
Л.М. Фридман [2] есептің құрамын талдап, ондағы келесі компоненттерді анықтайды:
аталған элементтер жиынын және олардың арасындағы байланыстар мен қатынастар жиынын қамтитын шарт;
мәселені шешу мақсатының көрсеткіші ретінде түсінілетін талап;
оператор, бұл тапсырма шартында оның талабын орындау үшін орындалуы тиіс әрекеттердің (операциялардың) жиынтығы
Н.Г. Каменкова [3] сонымен қатар төртінші компонентті - мәселені шешудің негізін анықтайды, ол шешімнің қандай да бір теориялық немесе практикалық негізі болып табылады. Н.Г. Каменкова мәселенің пайда болуын проблемалық жүйенің болуымен байланыстырады және мәселенің туындауының қажетті шарты ретінде проблемалық жүйенің проблемалық сипатын, яғни белгісіз элементтердің, қатынастардың болуын сезіну туралы айтады.
Психологияда мәселені қандай да бір субъект, мысалы, оқушы зерттеу объектісі (шешімін табу мақсатындағы талдау) ретінде қарастырады. Г.А. Балл [4] есеп ұғымы психологиялық әдебиеттерде үш түрлі категориядағы объектілерді белгілеу үшін қолданылатынын атап өтеді:
1) субъектінің әрекетінің мақсатының категориясы ретінде, субъект алдына қойылған талап;
2) жағдайдың категориясы ретінде, оның ішінде мақсатпен қатар оған қол жеткізуге тиіс шарттар;
3) осы жағдайды сөздік (белгі) тұжырымдау категориясы ретінде. Психологиялық әдебиеттерде есеп терминінің екінші категорияның объектісі ретінде жиі қолданылуы.
Математиканы оқытудағы есептердің рөлі мен функциясы Д.Пойа, Г.П.Бевз, А.Е.Әбілқасымова, Ю.М.Колягин [5], К.И.Нешков, В.И.Крупич, Л.М.Фридман [6], Л.Т.Искакова, Е.С.Канин, Р.С.Черкасов, А.А.Столяр және т.б. еңбектерінде қарастырған.
Американдық ғалым-математик Д.Пойа [7] есептің математикадағы рөлін қарастыра отырып, математиканы меңгеру стандартты есептерді шығару ғана емес, сонымен қатар дұрыс, түпнұсқалық, тапқырлық ойды талап ететін есептерді де шығара білу деп түсінеді.
Г.П.Бевз [8] бойынша есептің математиканы оқыту процесіндегі рөлі келесі түрде анықталған:
Оқушылар есепті шығару процесінде алған теориялық білімдерін практикада қолдана білуге үйренеді;
Есепті шығару процесі оқушылардың ойлауын және кеңістіктік елестетуін дамытуға мүмкіндік береді;
Ерік, табандылықты және т.б. тәрбиелеуге жағдай жасайды;
Оқушылардың ойлау процесін жандандырады, олардың шығармашылық қабілеттерін дамытады.
Осылайша, математиканы оқыту барысында есептердің маңыздылығы жоғары болып табылады.
Р.С.Черкасов пен А.А.Столярдың [9] Методика преподавания математики в средней школе кітабында математикалық есептердің жанжақты маңыздылығы көрсетілген: білім беру, практикалық, тәрбиелеу және ойлауды дамытудағы маңыздылығы.
Зейінді тәсіл оқушылардың белгілі бір есеп түрлерін шешу қабілетін дамытуға бағытталған; балаларды сөз есептеріне мағыналық-математикалық талдау жасауға, шарт пен сұрақтың, деректер мен қажеттінің арасындағы байланысты анықтауға және бұл байланыстарды схемалық және символдық үлгілер түрінде көрсетуге үйрету.
Тапсырмамен жұмыс істеудің белгілі бір алгоритмі бар. Келесі кезеңдерді бөліп көрсетуге болады. Біз жасайтын бірінші нәрсе - проблемалық мәлімдемені оқу. Шарт шамалардың белгілі және белгісіз мәндері туралы айтады. Содан кейін біз нені табуымыз керек екенін көрсетеміз, деректерді табамыз. Ал түпкі нәтиже біз іздеген нәрсе болады. Оқушылар шешу жолдарын іздеп, жоспар құрады.
Мәселелерді шешу қабілетін қалыптастыру - белсенділікті қалыптастыру. Іс-әрекеттің қалыптасуы мұғалімнің сабақ барысында арнайы ұйымдастырған жұмысына және таңдалған материалға тікелей байланысты. Педагогтың негізгі міндеті - балаларды қозғалысқа байланысты әртүрлі есептерді шығарғанда дұрыс ойлауға және оларды талдай білуге үйрету. Мұндай әрекет барысында кіші оқушы шешімге мәнді түрде жақындайды, оқу материалына деген қызығушылық қалыптасады.
М.А.Бантованың [10] пікірінше, есепті шешу дегеніміз нені таңдау керектігінің негізінде есептің шартымен көрсетілген мәліметтер мен ізделетіндердің арасындағы байланыстарды ашу, содан кейін есептеу әрекеттерін орындау және есептің сұрағына жауап беру.
Белгілі бір әдістемені қолдану кезінде мәселені шешу процесі кіші мектеп оқушыларының психикалық дамуына оң әсер етеді, өйткені бұл процесс ақыл-ой операцияларын орындауды талап етеді: талдау және синтез, салыстыру және жалпылау.
Оқушыларда есеп туралы түсінік қалыптастыру үшін мұғалім нақты мысалдар келтіріп, олармен әртүрлі жағдаяттарды талдауы қажет. Сабақта әрекеттің бұл түрін пайдалана отырып, бала қозғалыс мәселелеріне арналған тапсырмаларды орындаудың әртүрлі тәсілдерін меңгереді.
Есептерді шығару кезінде оларды игеру және өз бетінше пайдалану үшін оқушылар назар аударуы керек кейбір типтік эвристикаларды атап өтейік:
ақпаратты қайта кодтау, яғни бір тапсырманың әртүрлі үлгілерін құру;
есеп мәтінінен мағыналық бірліктерді оқшаулау, оларды түрлендіру және есептің шарты мен сұрағымен біріктіру, осы құрама есеп шарттарының бөлігінен қарапайым есеп құрастыру;
есептің сұрағын және оны шешу барысында туындайтын сұрақтарды көмекші сұрақтарға бөлу, осы сұраққа көмекші сұрақты таңдау;
пайымдау ағашын құру;
мәселенің шартын және (немесе) мәселесін баламаларға қайта тұжырымдау; жаңа объект функциясын ашу;
есеп шарттарының әртүрлі логикалық негіздерін бөліп көрсету;
берілгеннен нәтиже алу (берілген математикалық объектіден ондағы белгілерді сарқыту);
қойылған мақсатқа жетуге бағытталған мәселені шешу барысында алынған деректер мен нәтижелерге сұрақ қою (проблемалық сұраққа жауап беру);
ұқсастықты қолдану;
қосымша белгілер мен шарттарды енгізу;
аналитикалық, синтетикалық немесе аралас тәсілмен пайымдау тізбектерін құру. Олар белгілі бір эвристиканы ретімен қолдану процестерін білдіреді: берілгеннен нәтиже алу, проблемалық сұрақты көмекші сұрақтарға бөлу және т.б.;
есепті шешу жоспарын құру [11].
Анықталған эвристика өзара байланысты және өзара тәуелді; олардың біреуінің қалыптасуы бір мезгілде екіншісінің қалыптасуына ықпал етеді. Олардың кейбіреулері құрамы жағынан салыстырмалы түрде қарапайым, басқалары, керісінше, күрделірек. Алдағы уақытта бірінші сыныптан бастап оқушылар арасында жетекші эвристиканы анықтау және оларды қалыптастыру әдістемесін жетілдіру бойынша жұмысты жалғастыру керек.
Сонымен, есептерді шешу барысында оқушылар мынаны білуі керек:
есеп мәтінін оқу барысында диаграммадағы мәндерді бейнелеу;
сызба бойынша математикалық өрнектерді немесе формулаларды құрастыру;
өрнекті немесе оның сандық мәнін жазып, ауызша түрде сұраққа ауызша жауап беру;
есептерді жалпылама түрде шешу (бірдей шаманың әртүрлі өлшемдерінің арасындағы байланысты білу, әртүрлі типтегі есептердің жалпы құрылымын білу, есептерді шешудің ортақ әдісін қалыптастыру).

1.2 Бастауыш сыныпта қозғалысқа байланысты есептердің түрлері

Әдістемелік әдебиеттерде әдетте қозғалысқа арналған сөздік есептердің келесі түрлері бөлінеді:
қарсы қозғалысқа арналған тапсырмалар;
бір бағытта қозғалу тапсырмалары;
әртүрлі бағыттағы қозғалысқа арналған тапсырмалар;
су айдыны арқылы қозғалуға арналған тапсырмалар (тынық суда, өзен ағынымен, өзен ағынына қарсы).
Қозғалыс есептеріне үш шама кіреді: жылдамдық, уақыт, қашықтық, олар пропорционалдық қатынаспен байланысты [12].
Қозғалыс тапсырмаларының жіктелуін қарастырғанда мынаны атап өту керек: жай және құрама қимыл тапсырмалары ажыратылады [13].
Компонент қозғалысының міндеттері мыналарға бөлінеді:
бір бағытта қозғалу тапсырмалары,
объектілерді бір-біріне жақындату тапсырмалары;
объектілерді жою тапсырмалары,
өзен бойымен қозғалуға арналған тапсырмалар.
Сонымен қатар, кейбір қозғалыс тапсырмаларын қарастыруға болады:
төртінші пропорционалды табуға арналған тапсырмалар;
екі айырмашылықтан белгісізді табу есептері;
пропорционалды бөлуге байланысты есептер.
Жол - S, жылдамдық - V, уақыт - t ұғымдарымен оқушылар бастауыш сыныптан бері таныс.
Сонымен, бастауыш сынып оқушылары S V t біледі
(қашықтық жылдамдық пен уақытқа тең) жолдың формуласы. Ол кез келген заттың қозғалысына тән үш негізгі шама арасындағы байланысты белгілейді.

Негізінен қозғалыс есептері кем дегенде екі объектінің қозғалысын қарастырады [14]. Сондықтан қозғалыс есептері үшін сызбаларда қолданылатын келесі белгілерді енгіземіз:
S - объектілердің (жаяу жүргіншілер, велосипедшілер және т.б.) қозғалысы басталған нүктелер арасындағы қашықтық;
S1 - бірінші нысанның кездесуге дейін (немесе белгілі бір уақыт ішінде) жүріп өткен жолы;
V1 - бірінші объектінің қозғалыс жылдамдығы;
t1 - бірінші объектінің қозғалу уақыты;
S2, V2, t2 - екінші объект үшін ұқсас сипаттамалар.
Бір нүктеден бір бағытта қозғалысқа қатысты есептер

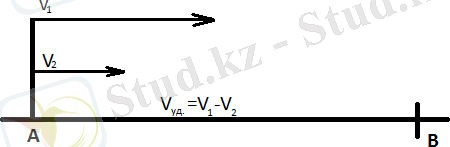
№1 тапсырма. Астанадан Алматыға бір бағыт бойынша екі ұшақ бір уақытта көтерілді. Бірінің жылдамдығы 1000 кмсағ, екіншісі 720 кмсағ. Бірінші ұшақ екіншісін 5 сағатта неше километр басып озады?

Шешімі:
1 әдіс
1) 1000 720 280 (кмсағ) - біріншісінің жылдамдығы екіншісінің жылдамдығынан үлкен.
2) 280 5 1400 (км) - біріншісі екіншісін басып озады.
Жауабы: 1400 (км).
2-әдіс
1) 1000 5 5000 (км) - бірінші ұшақ 5 сағатта ұшты.
2) 720 5 3600 (км) - екінші ұшақ 5 сағатта ұшып өтті.
3) 5000 3600 1400 (км) - біріншісі екіншісін басып озады.
Жауабы: 1400 км.
№2 тапсырма. Жүк көлігі мен жеңіл автокөлік бір уақытта А нүктесінен В нүктесіне шықты. Жеңіл автокөлік 60 кмсағ жылдамдықпен келе жатқан, жүк көлігі
45 кмсағ. Жеңіл автокөлік жүк көлігінен 50 км алда болу үшін қанша уақыт қажет?

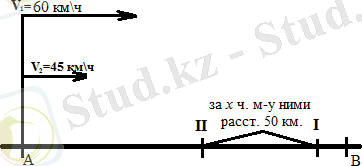
Шешімі:
1) 60 45 15 (кмсағ) - біріншісінің жылдамдығы екіншісінің жылдамдығынан үлкен.
2) 50:15 31 (сағ) - біріншісі екіншісінен 50 км алда болғанда.

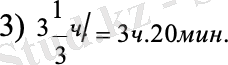
№3 тапсырма. Бір уақытта Семейден Өскеменге екі көлік аттанды, олардың жылдамдығы 70 кмсағ және 60 кмсағ болды. 2 сағаттан кейін машиналар арасындағы қашықтық қандай болады?

Шешімі:
1) 70 2 140 (км) - бірінші машина 2 сағатта жүрді.
2) 60 2 120 (км) - екінші машина 2 сағатта жүрді.
3) 140 120 20 (км) - 2 сағаттан кейінгі машиналар арасындағы қашықтық.
Жауабы: 20 км.
Ұзындығы 420 м болатын спорттық жолдың бойымен екі қыз бір мезгілде бір-біріне қарай жүгірді. Олар кездескен кезде біріншісі екіншісінен 60 м артық жүгірді. Әр қыз 30 секундтан кейін кездессе, қаншалықты жылдам жүгірді?
Мәселе екі қыздың бір-біріне қарай қозғалуында. Өздеріңіз білетіндей, қозғалыс үш шамамен сипатталады: қашықтық, жылдамдық және уақыт.
Мәселенің шарттары:
1. Екі қыз бір-біріне қарай жүгіреді.
2. Олар бір уақытта қозғала бастады.
3. Олардың жүгірген қашықтығы -420 м.
4. Бір қыз екіншісінен 60 метрге артық жүгірді.
5. Қыздар 30 с кейін кездесті.
6. Бір қыздың қозғалыс жылдамдығы екіншісінің қозғалыс жылдамдығынан артық.
Есепке қойылатын талаптар:
1. 1-ші қыз қаншалықты жылдам жүгірді?
2. 2-ші қыз қаншалықты жылдам жүгірді?

Қарама-қарсы бағыттағы қозғалысқа байланысты есептер
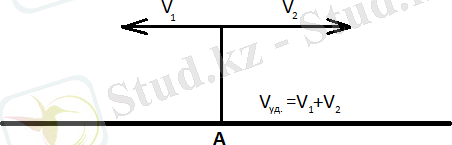Осы типтегі есептерді шешу кезінде жалпы жылдамдықтың басқа атауы болады. Қозғалыстағы заттардың уақыт бірлігінде алыстау қашықтығы жойылу жылдамдығы деп аталады. Қарама-қарсы бағытта қозғалған кезде алып тастау жылдамдығы қозғалатын объектілердің жылдамдықтарының қосындысына тең, яғни. Vsp V1 V2 .
№1 есеп. Екі ұл мектептен бір уақытта қарама-қарсы бағытта шықты. Біреуінің жылдамдығы 3 кмсағ, екіншісінің жылдамдығы 4 кмсағ. 2 сағаттан кейін ұлдар арақашықтығы қанша болады? Ұлдар бір-бірінен сағатына неше километрге жылжиды?
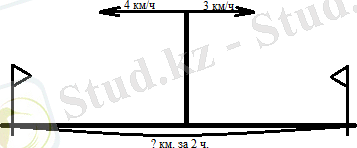Шешімі:
1) 4 3 7 (кмсағ) - шығару жылдамдығы (осы қашықтықта ұлдар 1 сағаттан кейін болады)
2) 7 2 14 (км) - 2 сағаттағы қашықтық.
Жауабы: 14 км.
№2 есеп. Екі спортшы бір стадионнан бір уақытта қарама-қарсы бағытта жүгірді. Біреуінің жылдамдығы 20кмсағ, ал екіншісінің жылдамдығы 23кмсағ. Бір сағатта спортшылар бір-бірінен қандай қашықтықта болады?

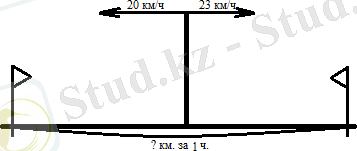
Шешімі: 1) 20 23 43 (кмсағ) - спортшылардың алыстап бара жатқан жылдамдығы, бұл да бір сағаттағы қашықтық болады. Жауабы: 43 км.
Су айдынындағы қозғалысқа есептер
№1 есеп. Көлдегі қайықтың жылдамдығы 20 кмсағ. Ол 4 сағатта қанша жол жүреді?
Шешімі:
Тапсырма - бір әрекетте бір бағытта қозғалыс формуласын қолдану:
1) 20 4 80 (км) - қайықтың жүріп өткен жолы.
Жауабы: 80 км.
Осылайша, әдістемелік әдебиеттерді талдау қозғалысқа арналған мәтіндік есептердің келесі түрлері болатынын көрсетті: келе жатқан қозғалысқа есептер, бір бағытта қозғалуға есептер, әртүрлі бағытта қозғалуға есептер, су қоймасының бойымен қозғалуға арналған есептер (тынық суда, өзеннің бойында, өзеннің ағысына қарсы); Оларды шешудің негізгі әдістері арифметикалық және алгебралық болып табылады.

1.3 Қозғалыс есептерін шешуді үйретудің әдістемелік ерекшеліктері

Қозғалыс есептерімен жұмыс істеудің көптеген әдістері бар. Оқушылар есепті шешуге толық саналы түрде келу үшін әрбір автор өзінің әдістемелік материалын өзінше ұсынады. Мұғалім өз кезегінде әр түрлі тәсілдерді зерттеп, қолайлысын таңдап алуы керек, оны кейін математика сабағында қолдана алады. Кейбір авторлардың қозғалыс тапсырмасымен жұмыс істеу әдістерін талдап көрейік.
Истомина Н.Б. [15] есепппен жұмыс істеу әдістемесін екі кезеңге бөледі:
I кезең - дайындық.
Ол бойынша бастауыш сынып оқушылары оқу дағдыларын меңгереді; ақыл-ой әрекетінің әдістемесі (анализ және синтез, салыстыру, жіктеу, аналогия, жалпылау); негізгі математикалық ұғымдардың мағынасын меңгеру: қосу, арттыру, алу, азайту, айырымды салыстыру; сегменттерді осы ұғымдарды модельдеу құралы ретінде пайдалануды үйрену, кесінділерді қосу және азайту дағдыларын меңгеру, диаграммамен танысу.
IІ кезең - негізгі. Ол бойынша оқушылар есептің құрылымымен (шарт, сұрақ, белгілі, белгісіз) танысады, оның мәтінін талдауды үйренеді (мұнда оның қарапайым немесе күрделі тапсырма екендігі маңызды емес), вербальды модельді мәтінге аударады.
4-сыныпта Истомина Н.Б. алдымен оқушыларды қозғалыс жылдамдығы ұғымымен таныстырады. Бірінші сабақта келесі мақсаттар көзделеді: оқушыларды жылдамдық ұғымымен таныстыру, жылдамдық шамасының өлшем бірліктері қарастырылады; Балалар жылдамдық пен қашықтықты табу есептерін шығаруды да үйренеді.
Қозғалыс есептерін шешу барысында мектеп оқушылары қозғалыстың белгілі бір орташа жылдамдықтары туралы түсінік қалыптастырады: жаяу жүргінші, велосипедші, моторлы кеме, моторист және т.б. Біркелкі және біркелкі емес қозғалыс туралы түсінік қалыптасады [16].
Тура және кері пропорционалды қатынасы бар қозғалыс есептерімен танысқанда есептерді шығару әдістерін жаттап алуға болмайды.
Содан кейін компонент тапсырмалары енгізіледі:
объектілердің келе жатқан қозғалысына;
объектілердің алыстауы;
бір бағытта қозғалу;
өзен бойымен қозғалу үшін [17].
Мектеп оқушылары қозғалыс есептерімен жұмыс істейді, оларды шешу әдісіне қарай есептер ретінде жіктеуге болады:
төртінші пропорционалды табу;
екі айырманы пайдаланып белгісізді табу;
пропорционалды бөлу арқылы.
Бекіту сабақ мазмұнына қозғалыстың әр түріне арналған есептерді, сонымен қатар әртүрлі тәсілдермен шешу жолдарын енгізу, одан кейін ең ұтымдысын таңдау арқылы жүзеге асырылады.
Қарсы қозғалыс және қарама-қарсы қозғалыс мәселелерін шешуге ерекше назар аудару керек.
Қарсы қозғалыстағы есептерді шешуге арналған оқыту әдісі оқушылардың осы мәселеге арналған сабақтарда жалпыланған біркелкі қозғалыс жылдамдығы туралы нақты идеяларына негізделген. Сөздердің мағынасы өмірлік бақылаулар негізінде бір-біріне қарай жылжу, қарсы бағытта, бір уақытта екі нүктені тастап, ... арқылы кездестік, т.б.
Есептерді шешу нәтижесінде оқушылар келесі байланыстарды меңгеруі керек:
қозғалыстың қашықтығы мен уақыты белгілі болса, онда жылдамдықты бөлу арқылы табу керек;
қозғалыс жылдамдығы мен уақыты белгілі болса, қашықтықты көбейту арқылы табу керек;
қашықтық пен жылдамдық белгілі болса, бөлу арқылы қозғалыс уақытын табу керек [18].
Содан кейін оқушылар алған білімдеріне сүйене отырып, құрама есептер шығарады, соның ішінде пропорционалды бөлуге, S, V, t шамалары бар екі айырмадан белгісізді табуға және төртінші пропорционалды табуға, құрама тапсырмалармен жұмыс істегенде сызбаларды пайдалану керек, өйткені сызба тапсырмада бейнеленетін өмірлік жағдайды дұрыс қолдануға, анықтауға және бейнелеуге көмектеседі.
Пропорционалды бөлуге есептер әртүрлі тәсілдермен енгізіледі: дайын есепті ұсынуға болады немесе алдымен оны құрастыруға болады, оларды шешкеннен кейін есептердің өзін де, шешу жолдарын да салыстыруға болады.
Оқушыларға есептер құрастырып, содан кейін оларды шешуге арналған жаттығулар және есептерді түрлендіруге арналған жаттығулар пайдалы. Бұл шешуге ұқсас есептерді құрастыру, есептерді олардың қысқаша схемалық белгілеулері бойынша құрастыру және шешу.
Қарсы келе жатқан қозғалысқа қатысты мәселелерді енгізбес бұрын, бір мезгілде қозғалыс туралы дұрыс түсініктерді қалыптастыру өте маңызды. Егер екі дене бір мезгілде бір-біріне қарай келсе, кездескенге дейін бірдей уақытты жүріп өтіп, барлық қашықтықты басып өтетінін оқушылардың анық түсінуі маңызды.
Осыдан кейін оқушыларды қарсы қозғалысқа байланысты есептерді шешумен таныстыру керек. Есептерді кері есептерге түрлендіру арқылы жаңа есептерді шығара отырып, бір сабақта барлық 3 типті енгізген жөн. Бұл әдіс балаларға шешімді өздері табуға мүмкіндік береді, өйткені балалар шешіп қойған есептен есептің жаңа түрі алынады.
Қазірдің өзінде келесі сабақтарда қарастырылған типтердің есептерін шығару қабілетін бекіту жұмыстары жүргізіледі [19].
Қарама-қарсы бағыттағы қозғалысты қамтитын есептер қарсы қозғалысты қамтитын тапсырмалар ретінде де ұсынылуы мүмкін. Дайындық жұмыстарын жүргізгеннен кейін оқушылар бір уақытта екі дененің бір нүктеден шыққан кездегі қозғалысын бақылауы қажет. Оқушылар мұндай қозғалыс кезінде қозғалатын денелердің арақашықтығы арта түсетінін білуі керек. Сонымен қатар сызбаның қалай жасалғанын көрсету қажет. Осы типтегі есептерді шығарумен танысқанда бір сабақта өзара кері үш есеп шығаруға болады, содан кейін алдымен есептердің өзін, содан кейін олардың шешімдерін салыстыруға болады.
Есептермен танысу кезінде мектеп оқушылары күрделі есеп пен қарапайым есептің негізгі айырмашылығын білуі керек. Мұндай мәселені бірден шешуге болмайтынын елестетіп көріңіз, яғни бір әрекетпен, оны шешу үшін деректер мен түпнұсқалар арасындағы байланыстардың тұтас жүйесін қалпына келтіре отырып, қарапайым тапсырмаларды таңдау керек. Сондай-ақ осы түрдегі құрама тапсырмалармен жұмыс жасауда балалардың қызығушылығын арттыратын, білім, білік, дағдының саналы дамуына ықпал ететін, ойлау, есте сақтау қабілетін дамытуға көмектесетін сызбаларды, ойын тапсырмаларын және дамытушылық тапсырмаларды пайдалану қажет [20].
Қорытындылай келе, есептер шығаруға үйрету әдісі оны қолдану нәтижесінде оқушылардың есеп шығару қабілетінің деңгейі жоғарылағанда тиімді болатынын атап өткіміз келеді; Шығармашылық жаттығулар күрделі есептерді шығару қабілетін дамытуға көмектеседі. Оларға қиындығы жоғары есептерді шешу, бірнеше шешімі бар есептерді шешу, есептерді бірнеше тәсілдермен шешу, жетіспейтін және артық деректері бар есептерді шешу, сонымен қатар есептерді құрастыру және түрлендіру жаттығулары жатады.

2 Бастауыш мектеп математикасындағы қозғалысқа байланысты есептермен эксперименттік жұмыс
Эксперименттік жұмысты анықтау кезеңі

Тәжірибелік жұмыстың бірінші кезеңі оқушылардың алғашқы диагностикасы болды. Тәжірибелік бөлімнің мақсаты: Қозғалыс есептерін шешуде қалыптасқан практикалық білімдердің болуын анықтау.
Бақылау жұмысы. №1 Қозғалыс мәселелері. 4-сынып.
1. Дұрыс анықтама алу үшін дұрыс әріпті таңдаңыз... . - бұл дененің уақыт бірлігінде жүріп өткен жолы.
а) қашықтық;
ә) уақыт;
б) жылдамдық;
в) басқа.
2. Көрсететін әріптерді дөңгелектеңіз:
a) жылдамдық s v m t p;
ә) уақыт s v m t p;
б) қашықтық s v m t p.
3. Қозғалыс жылдамдығын табу үшін қашықтықты уақытқа . . . қажет.
а) ұлғайту;
ә) көбейту;
б) азайту;
в) бөлу.
4. Қашықтықты табу үшін жылдамдықты уақытқа ... қажет.
а) көбею;
ә) көбейту;
б) кему;
в) бөлу.
5. Қозғалыс уақытын табу үшін қашықтықты жылдамдыққа ... қажет.
а) көбейту;
ә) көбейту;
б) кеміту;
в) бөлу.
Есептерді шешу. Оларға сызба салу
1- есеп. Моторлы қайық 3 сағатта 90 км жол жүрді. Содан кейін ол жылдамдығын 5 кмсағ төмендетіп, қалған қашықтықты 2 сағатта жүзіп өтті. Моторлы қайық барлығы неше километр жол жүрді?
2-есеп. Екі велосипедші екі қаладан бір-біріне қарай шықты. Біріншісінің жылдамдығы 14 кмсағ, екіншісінің жылдамдығы 12 кмсағ. Үш сағаттан кейін велошабандоздар кездесті. Қалалар бір-бірінен қаншалықты алыс?
Есепті шығар. Сызбадағы қателерді түзет.
3-есеп. А қаласынан екі пойыз әр түрлі бағытта жолға шықты. Бірінші пойыз 60 кмсағ жылдамдықпен жүріп В қаласына 5 сағаттан соң жетті. Екінші пойыз 80 кмсағ жылдамдықпен жүріп, 5 сағаттан кейін С қаласына жетті. В және С қалалары бір-бірінен қанша қашықтықта?

Осы тапсырмаларды орындағаннан кейін оқушылардың жұмысы алдын ала әзірленген критерийлер бойынша ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.