Математиканың сызумен байланысы

Мазмұны

Кіріспе

І. Негізгі бөлім

Математиканың физикамен байланысы

Математиканың экономикамен байланысы

Математиканың сызумен байланысы

Математиканың химиямен байланысы

Математиканың географиямен байланысы

ІІ. Қорытынды

ІІІ. Пайдаланылған әдебиеттер

Кіріспе

Қазіргі таңда бідім беру саласының мамандарының алдында тұрған басты мақсат - еліміздегі білім-ғылым жүйесін әлемдік стандарттарға сәйкестендіру, өзара бірлік-байланыста интеграциялау болып табылады.

Курстық жұмыстың мақсаты мен міндеттері:

Мақсаты: 5-6 сыныптарда математиканы оқыту барысында пәнаралық байланыстарды іске асыру.

Міндеттері:

• Математиканың басқа пәндермен пәнаралық байланысын анықтау;
• Математиканың басқа ғылымдарда атқаратын қызметін зерттеу.

Пәнаралық байланыс - түрлі оқу пәндер арасындағы өзара байланысты айқындау және білім беру мен оқыту талаптарының бірі болып табылады. Пәнаралық байланыстың қазіргі оқыту-тәрбиелеу, білім беру жүйесінде оқушылардың дүниетанымын тереңдете отырып, оқытудың тиімділігін арттыруға көмектесуі ғылыми педагогикалық дәлелдеме ретінде танылады. Оқушылардың әртүрлі пәндер бойынша берілетін теорияларды түсініп-білуі, олардың жалпы ақыл-ойына серпін туғызып, танымдық іс-әрекеттеріне шығармашылық сипат беріп, барлық алынған білімін жүйелейді.

Пәнаралық байланыстың пайдалы бір тұсы - жалпы оқу процесін, білім беру мекемесінің барлық жұмысын бір жолға салуға, ғылымдар жүйесінің бір арнаға тоғысуына септігін тигізеді. Барлық мұғалімдерге бірдей талап қоюға және әр түрлі пәндерге ортақ мүддені шешуге ықпал етеді.

Пәнаралық байланысты жүзеге асырудың мынадай жолдары бар:

• Пәнаралық байланысты анықтау мақсаты;
• Өзара байланысқа түсетін оқу пәндерін саралап, іріктеп алу;
• Байланыс бөлігі немесе бөлігі болған оқу пәндерінің әрқайсысының ерекшеліктерін анықтау.

Негізгі бөлім

Пәнаралық байланысты жүзеге асыру, жоғары оқу орындарында сондай-ақ орта білім беру мекемелеріндегі негізгі ерекшеліктердің бірі болып табылады. Әсіресе бұл міндетті шешу математика ғылымы үшін өзекті мәселе болып қала бермек.

Пәнаралық байланыс - педагогика ғылымында философиялық, психологиялық, дидактикалық және әдіснамалық жағынан қарастырылатын күрделі комплексті сала. Сонымен бірге, пәнаралық байланыс педагогика ғылымының басты мәселесі болуымен бірге қазіргі заманғы ғылымдардың интеграциялану тенденциясы жағдайында мектеп жүйесінің білім беру мазмұнын айқындаудың басты ерекшеліктері болып саналады. Пәнаралық байланыстарды оқыту процесінде қазіргі заманғы ғылыми танымның маңызды белгілерін құрайтын ғылымаралық байланыстардың көрініс табуы ретінде қарастыру керек.

Пәнаралық әр түрлі ғылым негіздерін оқытудың мақсаты мен мазмұнының ұштасуына, сондай ақ оқушылардың білімі мен нанымын қалыптастыруға, олардың іскерліктері мен танымдық қабілеттерін дамытуға бағытталады.

Қысқаша айтқанда, пәнаралық байланыстар оқу-тәрбиелеу жұмыстарының мазмұнында, формасы мен әдістерінде өз бейнесін тапқан және білім беру, дамыту мен тәрбиелеу функцияларын атқаратын нақты болмыс объектілері, құбылыстары және процестерінің арасындағы синтездеуге, интегралдауға ұшырайтын қарым-қатынастарды бейнелейтін педагогикалық категория болып табылады.

Пән арасындағы байланыстарды жүзеге асыру әр түрлі білім салаларының арасында айқын шекара жоқ екенін, олар бір бірінен қол үзбейтінін, әр сала өз әдіс тәсілдері мен материялық дүниені зерттейтініне оқушылардың көзін жеткізеді.

Оқу пәндерінің арасындағы байланыстың екі типі бар:

1. Уақыттық (хронологиялық)

2. Ұғымдық ( идеялық)

Бұлардың біріншісі әр түрлі пәндердің программалық материалдарын оқытуды уақыт бойынша келісуді, екіншісі ғылыми ұғымдарды жалпы методологиялық қағыдалар негізінде біркелкі түсіндіруді көздейді.

Әр пәндегі жеке тақырыптар мен тарауларды оқытуды уақыт бойынша мәмілеге келтіру олардың программаларын сәйкестендіру арқылы қамтамасыз етіледі.

Мысалы: 5 сыныпта оқушыларда бағы ұғымы қалыптаса бастайды және бұл ұғым 7 сыныптың геометрисында дамытылады. Бағыт туралы алғашқы ұғымының негізінде 7 сыныпта физика пәнінде күш ұғымын векторлық шама ретінде, одан соң бір түзудің бойында бір жаққа қарай немесе қарама-қарсы бағыттылған екі күштің қосындысын үйрене бастайды. Вектор ұғымының геометрия оқулығында сипаттамасы оның физикалық түсіндірмесінен бұрын беріледі. Сондықтан, оқушылар геометрияда да, физикада да вектор деп аталатын ұзындығы мен бағыты арқылы танысады.

Пәнаралық байланыстарды былай да көрсетуге болады:

1. Есептерді шешу барысында алгоритмді сипаттау және құрастыру, оларды іске асыруда математикамен байланысты.

2. Электронды - есептеу машынасының құрылымы, техникалық құрылымдарының өзіндік жұмыс режимі олардың сипаттамасы және параметрлерін оқып үйренуде физикамен байланысы.

3. Алгоритмдік тілдерді және электронды-есептеу машынасының тілдік жабдықталуы - лингвистикалық аспектімен байланысы, мәтіндерді шифрлау, мәтінді аппараттарды өңдеу және синтаксистік талдау, аударма жасау, сөздікті ұйымдастыру және сөзді іздестіру.

4. Бағдарламалау негізінен үйренудегі байланыс: лингвистикалық мәдениеттің қалыптасуы, ол ойдың қысқа және логикалық бейнеленуі, мәтіндердің негізгі және құрама бөліктерін көрсету, талдау жүргізу, бақылау, анытамалық ақпараттармен жұмыс істеу.

5. Электронды-есептеу машынасын пайдалану заңдылықтары басқа пәндеріне компьютерді техникалық оқу құралы ретінде тиімді пайдалану қадамдары болып табылады.

Математиканың физикамен байланысы:

Физика сабақтарында мұғалім математикалық тәсілдерді жиі қолданады:

• Заңдарды жалпы және дәл формада өрнектеу үшін,
• Кейбір теориялық алғышарттардың заңдылықтарын қорытындылау үшін;
• Шығарып алынған формулаларды басқаға түрлендіру үшін;
• Тікелей өлшеуге мүмкін болмайтын шамаларды табу үшін.

Физиканы оқытудағы математикалық тіл заңдары және тәжірибелі зерттеулердегі заңдарды қысқаша өрнектеудің, көптеген негізгі ережелердің теориялық түсіндірілуі үшін қолданылатын құрал.

Физикалық есептерді шығарғанда мұғалім математиканы жиі қолданады.

Физика курсын оқытудың басында оқушылар символдарды және әріптік формулаларды қолдануға әдеттенеді. Математиканың белгілі бір курсын оқығаннан кейін оқушылар физикалық шамалардың арасындағы қатынастарды қысқа, ықшам жазу үшін, ал содан кейін есептеулерді жүргізу үшін қызмет атқаратынын түсінеді.

Жоғары сыныптарда физиканы оқытуда математиканың ролі ерекше жоғарылайды. Мұнда физикалық құбылыстарды экспериментальды оқытумен бірге физика мұғалімі физикалық зерттеуде мтематикалық анализді кең қолдануына болады, өйткені бұл оқушылардың математикалық дайындық деңгейі бойынша мүмкін. [15, 104-107]

Математиканың экономикамен байланысы

Экономикалық мазмұндағы, яғни шешуі математикалық аппараттың қолданылуын талап ететін экономика саласында қойылған есептерді қарастырайық. «Қазіргі замандағы қоғам экономикаландырылған өмірде тұрады, ал мектеп математикасы (басқа да пәндер) бұл ерекшеліктерді еш елемейді» деп А. С. Симонов айтқан [13, 16], сондықтан да математиканы оқыту саласындағы осы заманда көптеген зерттеушілер мектеп математика мазмұнына экономикалық мазмұндағы есептерді енгізу қажеттегін атап айтты.

Экономикалық мазмұндағы бірнеше есеп қарастырайық. Мұндай есептер, біздің ойымызша, оқушылардың білімдерін жаңғыртып, олардың оқуға деген себептерін жоғарылатып қана қоймай, сонымен бірге оқушыларда танымдық қызығушылықтарын оятады.

1-есеп. Салымшы шот ашып, оған қарапайым (капиталға айналдырусыз) мөлшерлеме бойынша жылдық пайызы 11, 5 болатын 4 жылға 25000 теңге көлемінде ақша салды. Салымшы салымның жабуында алатын сома қандай болады? 4 жылдың ішінде салым қанша теңгеге өседі? Арттыру коэффициенті неге тең (яғни салым сомасы қанша пайызға өседі) ?

Шешуі . Белгілеулер енгізейік. $S_{0}$ - алғашқы капитал, p - пайыздық мөлшерлеме, n - толық жыл саны, $S_{n}$ - n -ші жылдың соңында пайыздармен есептелген капиталдың сомасы.

Онда Тогда қарапайым пайыздарды есептеу жолымен салымның қызмет ету моделі келесі түрде есептеледі:

$$S_{n} = (1 + \frac{n \cdot p}{\text{100}}) \cdot S_{0}\text{. }$$

Осы формула берілген экономикалық есептің математикалық моделін өрнектейді.

Есептің берілгендерін қолданып, есептеулер жүргізейік. n=4 , p=11, 5 , ал $S_{0} = \text{25000}$ болғандқтан

$S_{2} = (1 + \frac{4 \cdot \text{11}, 5}{\text{100}}) \cdot \text{25000} = 1, \text{46} \cdot \text{25000} = \text{35} = \text{36500}$ болатынын аламыз.

4 жылдан кейінгі салым сомасы 36500 теңге, яғни салым 11500 теңгеге өседі.

Қарапайым пайыздарды арттыру коэффициенті деп $\frac{S_{n}}{S_{0}} = 1 + \frac{n \cdot p}{\text{100}}$ қатынасын айтады.

Бұл қатынас алғашқы $S_{0}$ салымының осы соманың банкте p% жылдық мөлшерлемемен қарапайы пайыздар сүлбесі бойынша n жыл сақталуы ішінде қанша есе өскенін көрсетеді. Берілген есепте арттыру коэффициенті 1, 46 -ға тең.

2-есеп. Банктен 40 мың АҚШ доллары көлемінде 8 жылға төмендегі шарттар бойынша несие алынды: алғашқы үш жылға жылдық пайыздық мөлшерлеме 28%, келесі жылы ол 2%-ға артады, қалған жылдарға тағы да 2, 5%ға артып отырады. Несие қайтару мерзімінің соңында күрделі пайыздардың жылдық есептелуінде банкке қайтарылуы қажет соманы табыңдар. (Күрделі пайыз (немесе басқаша айтсақ «пайызға пайыз») - бұл бірінші кезеңде жиналған сома бастапқыға қосылғандағы капиталдың көбеюі, яғни, экономика тілімен айтсақ, бастапқы сома капиталға айналады да, жаңа кезеңде пайыз басқа, ұлғайтылған сомаға есептеледі. )

Шешуі . Барлық мерзімді жылдық пайыздық мөлшерлемеге тең кезеңдерге бөлейік. Бірінші кезеңде жылдық p ₁ % есептеп қосылады, кезең ұзақтығы - n ₁ жыл, сосын n ₂ жыл жылдық p ₂ % есептеп қосылады және ұзақтығы n ₃ жыл болатын үшінші кезеңде есептеу p ₃ % болады және т. с. с. Онда бірінші кезеңде келесі сома есептеледі:

$$S_{1} = S_{0}(1 + \frac{p_{1}}{\text{100}}) ^{n_{1}},$$

Екінші және үшіншіде сәйкесінше:

$S_{2} = S_{1}(1 + \frac{p_{2}}{\text{100}}) ^{n_{2}}$ және $S_{3} = S_{2}(1 + \frac{p_{3}}{\text{100}}) ^{n_{3}}$

және т. с. с.

Сондықтан, n=n ₁ +n ₂ +…+n _k жыл өткесін арттырылған S сома мынаған тең

$$S = S_{0} \cdot (1 + \frac{p_{1}}{\text{100}}) ^{n_{1}} \cdot (1 + \frac{p_{2}}{\text{100}}) ^{n_{2}}\text{ . . . } \cdot (1 + \frac{p_{k}}{\text{100}}) ^{n_{к}}$$

Біздің есепте үш кезең бар. Бірінші кезеңде жылдық 28% есептеледі, кезең ұзындығы - 3 жыл, сосын 1 жыл 30% есептеп қосылады, және үшінші кезең - 4 жыл - 32, 5% есептеп қосылады. Онда бірінші кезең бойынша келесі сома есептеледі:

$$S = \text{40} \cdot (1 + \frac{\text{28}}{\text{100}}) ^{3} \cdot (1 + \frac{\text{30}}{\text{100}}) ^{1} \cdot (1 + \frac{\text{32}, 5}{\text{100}}) ^{4} = \text{40} \cdot 1, \text{28}^{3} \cdot 1, 3 \cdot 1, \text{325}^{4} \approx \text{336}, \text{122}$$

Қайтару сомасы доллар дәлдікпен 336, 122 мың АҚШ доллары.

3-есеп . Сұраныстың бағасы мен өлшемінің қатынасы кестеде берілген. Икемділік коэффициентін анықтау қажет. Сатушының іс-әрекетін бағалау.

2. 2. 2. 1 кестесі

Шешуі:

$E_{p} = \frac{{\Delta Q}_{d} \cdot P}{\Delta P \cdot Q_{d}}$ ; $E_{p} = \frac{(\text{20} - \text{15}) \cdot \text{50}}{(\text{60} - \text{50}) \cdot \text{20}} = \frac{\text{250}}{\text{200}} = 1, \text{25}\ \ 1$

Қорытынды: Сұраныс икемді. Сатушының іс-әрекеті дұрыс емес, өйткені сұраныстың икемділік шарттарында бағаны көтеру емес төмендету пайдалы.

2. 2. 2. 2 кестесі

Шешуі:

$E_{p} = \frac{{\Delta Q}_{d} \cdot P}{\Delta P \cdot Q_{d}}$ , $E_{p} = \frac{(\text{20} - \text{18}) \cdot \text{40}}{(\text{45} - \text{40}) \cdot \text{20}} = \frac{\text{80}}{\text{100}} = 0, 8\$

Қорытынды: Сұраныс икемді емес. Сатушының әрекеті дұрыс, өйткені сұраныстың икемді емес жағдайында бағаны аздап көтеру пайдалы. Действие продавца верное, т. к. в условиях неэластичного спроса выгоднее осуществлять незначительное повышение цены.

Осы есептердің шығарылуынан жасалған қорытындыны кесте түрінде көрсетейік.

Егер баға мен түсім қарама-қарсы бағытта өзгерсе, онда біз икемді сұраныс тауарын аламыз. Егер түсім мен баға бір бағытта өзгерсе, онда икемді емес сұраныс тауары болғаны.

2. 2. 2. 3 кестесі

4-есеп. Тауар бағасы мен сұраныс өлшемінің қатынасы Q= 38-3p функциясымен берілген. 5 теңге және 7 теңге бағадағы икемділік коэффициентін анықтаңдар.

Шешуі:

Q _d =38-3p $E_{p} = Q_{d'} \cdot \frac{P}{Q_{d}}$

p ₁ = 5т . $E_{p} = (\text{38} - 3P) ' \cdot \frac{P}{\text{38} - 3P} = \frac{3P}{\text{38} - 3P}$

= 7т. $E_{p_{1}} = \frac{3 \cdot 5}{\text{38} - 3 \cdot 5} = \frac{\text{15}}{\text{23}} = 0, \text{65} < 1$

$E_{p_{2}} = \frac{3 \cdot 7}{\text{38} - 3 \cdot 7} = \frac{\text{21}}{\text{17}} = 1, \text{24} > 1$

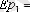
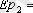
Қорытынды: Тауардың бағасы 5 теңге болғанда сұраныс икемді емес. 7 теңге болғанда сұраныс икемді болады.

5-есеп. Тауар бағасы мен сұраныстың өлшемінің қатынасы Q _d =21-5P функциясымен берілген. Қандай бағада тауарға сұраныс икемді емес (Е _р = 0, 9) немесе икемді (Е _р = 1, 1) болады.

Шешуі:

$$E_{p} = Qd' \cdot \frac{P}{\text{Qd}}$$

$E_{p_{1}} = 0, 9$ $E_{p} = (\text{21} - 5P) '\frac{P}{\text{21} - 5P} = \frac{5P}{\text{21} - 5P}$

$E_{p_{2}} = 1, 1$ 1) $0, 9 = \frac{5P}{\text{21} - 5P}$ 2) $1, 1 = \frac{5P}{\text{21} - 5P}$

p ₂ -? 5P=0, 9 (21-5P) 5P= 1, 1(21-5P)

p ₁ -?

5P=18, 9-4, 5P 5P= 23, 1 -5, 5P

9, 5P=18, 9 10, 5P=23, 1

P ₁ =1, 99 P ₂ =2, 2

Қорытынды. Тауардың құны P=2, 2 теңге болғанда сұраныс икемді болады, құны P=1, 99 болса сұраныс икемді емес. [14, 10]

Оқушылардың назарына математикалық модельді құруда қарапайым және күрделі пайыздар аппаратын қолданатын қолданбалы есептер мысалы ретінде қаражат сипатындағы есептерді ұсынуға болады.

Экономика мазмұнындағы есептер практикалық есептер болып табылады. Ал оларды шығару орта мектеп математика мазмұнын сапалы игеруге мүмкіндік береді, алған білімдері мен іскерліктерін экономикаға аудару мүмкіндігін береді. Ал бұл оқушылардың қолданбалы сипаттағы есептерге және жалпы математикаға деген қызығушылықтарын белсендіреді. Мұндай есептер оқытудың қолданбалылық бағыттылығын толығымен жүзеге асыруға және оқу материалының өзін сапалы түрде игеруге және осыған ұқсас есептерді шығару іскерлігін қалыптастыруға мүмкіндік туғызады.

Математиканың сызумен байланысы

Осы екі пән мектеп курсында материалдық өмірдегі кеңістік формаларын және кеңістік қатынастарды зерттеумен айналысады.

Математика бағдарламасының түсініктеме хатында геометрияны оқытудың мақсаты жазықтықтағы фигуралардың қасиеттерімен таныстыру, кеңістіктегі елестетуді дамыту болып табылады. Мұнымен қатар практикалық дағды мен іскерлік қалыптасуы керек, бұған өлшеулерді орындау, практикалық сипаттағы әртүрлі есептерді шығару іскерліктері де кіреді. Осы есептер сызу сабақтарында да шығарылады; осы пәндерді оқытудағы байланыстардың қажеттілігі геометрияда да, сызуда да оқушылардың сызбалар орындауымен түсіндіріледі. Сонымен қатар геометрия сызу пәні үшін теориялық негіздер береді, ал сызу пәнін оқу процесінде қалыптасатын салу дағдылары геометрия пәнінде қолданылады. Сызу мұғаліміне оқу материалын түсіндіру барысында оқушылардың геометрия курсынан алған теориялық мәліметтеріне жиі сүйену қажет болады. Сол сияқты геометрия мұғалімдері салумен байланысты сұрақтарға үлкен назар аударуралы қажет.

Кейбір геометриялық есептерді графиктік түрде шығарғанда циркуль және сызғышпен ғана шектелмеу керек, өйткені бағдарлама салу есептерін шығаруды үйретуде көп құралдардың қолануын талап етеді. Геометрия сабақтарында сызу құралдарының рационалды қолданылуы, бір жағынан, сызуға арналған есептерді тиімді шығаруға мүмкіндік берсе, екінші жағынан, сызу сабақтарындағы сызбаларды орындауда қолданылатын белгілі дағдылардың жасалуына мүмкіндік береді. Осы міндеттің орындалуы үшін геометрия сабақтарында перпендикуляр түзулерді салуда тек бір сызба бұрыштығын ғана емес, бұрыштық пен сызғышты немесе екі бұрыштықты қолданылу қажет.

Геометрия сабақтарында параллелограммды, ромбты, трапецияны, шеңберге жанаманы және т. б. сызуға байланысты басқа да есептер қарастырылады. Барлық аталған есептер рациональды яғни сызу сабақтарында және конструкторлық бюро жұмыстарының практикасында қолданылатын тәсілдермен шығарылуы өте маңызды. Осы есептерді бұрыштық және сызғыш көмегімен шығаруда мұғалім қандай да бір есепті терең талдау, дәлелдеу және зерттеуге қажетті уақытты үнемдейді.

Сызудағы кейбір шартты кескіндеулер геометрия сабақтарында рационалды қолданылуын табылуы орынды.

Мұнда сызба сызықтарымен, шрифтпен және өлшемдерді белгілеумен байланысты мемлекеттік стандарттың қолданылуы туралы айтылды. Бұл геометриялық сызбалардың сапасын жақсартуға, түсінікті және жетілуіне мүмкіндік береді. Салуға арналған есептерді шығарғанда оқушыларға сызу сабақтарында да, математика сабақтарында да бірдей талап қою керек.

Сызу сабақтарында оқушылар теориялық білімді бекітеді, есептеу дағдыларын шынықтырады, құрастыру дағдыларына иемденеді.

Математиканың химиямен байланысы

Математиканың химиямен байланысын мысал ретінде қарастырайық. 8-сыныптағы «Химиядағы сандық қатынастар» тақырыбын оқуда оқу бағдарламасының келесі мәселесі қалай шешілгенін қарастырайық: “ Егер 6, 72 м ³ газ қоспасы бар ыдыстың 1/3-і азотпен және 2/3-і сутекпен (көлем бойынша) толтырылса, ыдыстағы газдардың массалық қатынастары 7:1 қатынасындай болатыны туралы ұйғарым ақиқат па?”

Көрсетілген мәселе тек химия, математика және физика пәндерінің өзара байланысын құру негізінде ғана шешіледі. Сондықтан Сабақ барысында туындайтын танымдық мақсат осы барлық үш пәнді де қолдануы керек.

Математика элементтері химия мен физика беретін мазмұнды жағдайларын күшейту үшін қолданылады.

Сабақта келесі математикалық дәлелдеулер жүргізіледі:

1. Көлемі 1 м3 болатын азот массасы 1, 25 кг-ға тең. Егер M = 28∙10 ^-3 кг/моль, ал V _m = 22, 4∙10 ^-3 м ³ /моль болса, онда ρ = M/V _m формуласы бойынша ρ=1, 25 кг/м ³ табамыз. Көлемі 1 м ³ азот массасы m = ρ∙V теңдеуімен есептеледі. Берілген жағдайда ρ жіне m сандық мәндері беттеседі m=1м ³ ·1, 25кг/м ³ = 1, 25 кг.

2. Көлемі 1м ³ сутек массасы 0, 089 кг-ға тең. Егер M = 2∙10 ^-3 кг/моль, ал V _m = 22, 4∙10 ^-3 кг/моль, онда ρ = M/V _m формуласы арқылы ρ = 0, 089 кг/м ³

Көлемі 1 м ³ сутек массасы m = ρ∙V теңдеуімен анықталады. ρ және m сандық мәндері беттеседі m = 1м ³ ∙0, 089 кг/м ³ =0, 089 кг.

3. Азот және сутек қоспасының көлемі 6, 72 м ³ тең. Азот пен сутектің көлемдік қатынасы $\frac{1}{3}:\frac{2}{3}\text{. }$ Ыдыстағы газдардың массалық қатынасы 7:1 қатынасындай екенін дәлелдеу қажет.

Шешуі:

Азот көлемі V=1/3∙6, 72 м ³ =24 м ³

Сутек көлемі V=2/3∙6, 72 м ³ =4, 48 м ³

m = ρ∙V формуласы бойынша азот пен сутек массаларын табамыз.

Азоттың массасы m=1, 25 кг/м ³ ∙2, 24 м ³ =2, 8 кг .

Сутектің массасы m=0, 089 кг/м ³ ∙ 4, 48 м ³ =0, 4 кг .

Азот пен сутектің 1/3: 2/3 көлемдік қатынастарынан массаларының қатынасы 2, 8 (кг) : 0, 4 (кг) болады, осыдан берілген ыдыстағы газдардың массалық қатынасы 7:1 қатынасындай деген ұйғарымның ақиқаттығын көрдік.

Шығарудың жоспарын құрғанда күрделі есеп бір-бірімен есептің жалпы мазмұнымен байланысты болатын бірнеше қарапайым есептерге жіктеледі. Есепті шығарудың жоспарын құрастырғанда, екі негізгі әдіс қолданылады:

а) синтетикалық;

б) аналитикалық.

Осы әдістердің әрбіреуін мәнін нақты есептің шығару жоспарын құру мысалымен қарастырайық.

... жалғасы

Vii-ix сыныптарда математиканы оқыту барысында пәнаралық байланыстарды жүзеге асыру

Математика сабақтарында пәнаралық байланыстарды арттыру

Математиканың ерекшелігі - оның қолданылымының әмбебаптығы

Математика сабағында оқушылардың белсенділігін арттыруда пәнаралық байланыстын ықпалы

Бастауышта арифметикалық амалдарды үйрету әдістемесі

Арифметикалық амалдарды орындау тәсілдері

МАТЕМАТИКАНЫ ОҚЫТУ ӘДІСТЕМЕСІНІҢ ЖАЛПЫ МӘСЕЛЕЛЕРІ

Ересектер тобындағы балаларға арифметикалық, есептеу туралы түсінік беру

Сызуды оқыту әдістерінің түрлері

Арифметика және алгебраға тиісті үйірме жұмыстары

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс