Алгебралық теңдеулер жүйесінің анықтамасы

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ ЖОҒАРЫ БІЛІМ МИНИСТРЛІГІ

«ҚАЗАҚ ҰЛТТЫҚ ҚЫЗДАР ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ» КеАҚ

Физика математика және цифрлық технологиялар институт

Математика кафедрасы

Жобалық ЖҰМЫС

Пән аты: қолданбалы есептерді математикалық моделдеу

Тақырыбы: «Алгебралық теңдеулер жүйесі: қолдамбалы есептың математикалық моделі Алгебралық теңдеулер жүйесінің анықтамасы, қасиеттері, шешілімділігі. $\gg$

Мамандық атауы, курс: Математика-7М01501, 1 курс

Орындаған: Мәуіт Нұрзия

Оқтушы: профессор Асанова А. Т

Алматы, 2024

мазмұны

1. Жобалық жұмыстың паспортын рәсімдеу3-бет

2. кірспе4-бет

3. негізгі бөлігі : теориялық бөлім және практикалық бөлім. . 5-бет

4. Қортынды . 14-бет

5, Қосымща:

қолданылған әдебиеттер тізімі. .

Антиплагиат өту анықтамасы

Жобалық жұмыстың паспортын рәсімдеу -жобаның мақсаты, міндеттері мен өзектілігі

Жобалық жұмыс«Алгебралық теңдеулер жүйесі: қолдамбалы есептың математикалық моделі, Алгебралық теңдеулер жүйесінің анықтамасы, қасиеттері, шешілімділігі. $\gg$

Мақсаты :алгебралық теңдеулер жүйесіне нақты түснік қалыптастру, Алгебралық теңдеулер жүйесінің анықтамасын біліу, қасиеттерін айқындау, шешімділігін көрсету қолданбалы есептердің математикалық моделің беру.

Жұмыстың негізгі міндеттері: 1) алгебралық теңдеулер жұйесін жалпы жақтан түсіну;

2) алгебралық теңдеулер жүйесіне анқтама беру, қасиеттерін көрсету;

3) зерттеу нысаны - алгебралық теңдеулер жүйесі, олардың қазіргі күйі және оларды шешу жолдары;

4) қолдамбалы есептың математикалық моделі алгебралық теңдеулер жүйесінде қалай қолдануды көрсету;

Өзектілігі : Бұл тақырып өзекті, себебі алгебралық теңдеулер жүйесін шешу - есептеу алгебраның негізгі мәселелерінің бірі. алгебралық теңдеулер жүйесін шешу мәселесі қолданбалы есептер үшін салыстырмалы түрде сирек тәуелсіз қызығушылық тудыратынына қарамастан, компьютердің көмегімен көптеген процестерді математикалық модельдеу мүмкіндігінің өзі көбінесе осы жүйелерді тиімді шешу мүмкіндігіне байланысты. Әртүрлі (әсіресе сызықтық емес) есептерді шешудің сандық әдістерінің маңызды бөлігіне сәйкес алгоритмнің элементар қадамы ретінде алгебралық теңдеулер жүйесін шешуге кіреді. алгебралық теңдеулер жұйесын шешу әдістері сандық әдістер куысынің негізгі бөлімдерінің бірі болып табылады . ғылми-техникалық есептер жұмыстарын жүргізу, сол сиақты инженерлік зерттеулер кезінде Т Б. көптеген жағдайларда алгебралық теңдеулер жүйесін шешуге тура келеді . сондықтан қолданбалы математика, информатика және математика мамандықтары бойынша студенттерлі жоғары мектеп талаптарына сай дәрежеде дайындау қазіргі заманнің өзекті мәселелерінің бірі болып табылады. [1]

Кіріспе

Бұл жобалық жұмысымда жалпы алгебралық теңдеулер жұйесіне жалпы жақтан тоқтала кеттім және алгебралық теңдеулер жұйесіне анықтама беріп, оның қасиеттерын мен ерекшелыктерін айқындадым . алгебралық теңдеулер жүйесінің қазіргі күйі және оларды шешу жолы жәйлы тоқтала кеттім. математикалық моделдеудің жалпы қолдану аиясынатоқтала кеттім. Математиканы оқытудың негізгі мақсаттарына қарапайым нақты құбылыстардың математикалық модельдерін құру, берілген модельдер арқылы құбылыстарды зерттеу және модельдердің қолданбалы жобаларын құрастыру дағдыларын дамыту жатады. Бұл мақсатқа жету құралдарының бірі математикалық модельдеу әдісі болып табылады. Математикалық модельдеу сөздің тар мағынасында нақты физикалық, химиялық, технологиялық, биологиялық, экономикалық және басқа да процестердің теңдеулер мен теңсіздіктер түріндегі сипатталуы ретінде түсініледі. Әртүрлі процестерді талдау мен синтездеудің математикалық әдістерін қолдану үшін бұл процестерді математика тілінде сипаттай білу, яғни теңдеулер мен теңсіздіктер жүйесі түрінде сипаттау қажет. Модельді құру кезінде оның дамуына ықпал ететін синтез, салыстыру, жіктеу, жалпылау арқылы талдау сияқты ойлау операциялары қолданылады.

Математикалық модель құрастыру және есепті математика тіліне аудару студенттерді болашақ кәсіби іс-әрекетінде нақты процестер мен құбылыстарды модельдеуге дайындайды. Математикалық модельдеу қызметтің экономикалық және ғылыми салаларында ерекше рөл атқарады. Экономикадағы көлік есептерін шешуде математикалық модельдеуді, сонымен қатар Марков тізбектері теориясындағы және ықтималдықтар теориясындағы есептердегі математикалық модельді қолдануды қарастыратын болсақ, Осылайша біз әртүрлі салаларда математикалық модельдеудің маңыздылығын көрсетеміз.

Бір үлгідегі мәселені шешудің көптеген әртүрлі әдістерін ұсынуға болатыны белгілі. Ықтималдықтар теориясы мен математикалық статистикада Орталық шек теоремасының тарихы жақсы белгілі, ол көптеген әртүрлі әдістермен алынған, Модельдеу арқылы есептерді шешу кезінде оқушылар өмірдегі проблемалық жағдаяттарды абстрактілі модельдерге және керісінше аударуды үйренеді. Модельдеуді қолдану оқу процесінің шығармашылық бағытын арттыруға, ақыл-ой қабілеттерін дамытуға, сол арқылы жалпы ғылымның дамуына ықпал етеді. . [2]

негізгі бөлігі : теориялық бөлім

1. Алгебралық теңдеулер жүйесінің анықтамасы

Алгебралық теңдеулер жүйесі деген ­-бірлесіп (бірге) шешетін теңдеулер жиынтығын айтады. Негізгі алгебралық жүйе екі айнымалысы бар екі сызықтық теңдеуден тұрады алгебрада екі немесе одан да көп теңдеулерді бірге шешу (яғни, шешім жүйедегі барлық теңдеулерді қанағаттандыруы керек) .

Алгебралық теңдеулер жүйесі төмендегідей түрлері жиі кезігеді

Сызықтық алгебралық теңдеулер жүйесі

Бір айнымалсы бар квадраттық теңдеулер жүйесі

Екі айнымалсы бар квадраттық теңдеулер жүйесі

Тригонометриялық теңдеулер жүйесі

1, 2Алгебралық теңдеулер жүйеснің қасиеттері

Алгебралық теңдеулер жүйесі түрлеріне тоқталып өтейік, Теңдеулер жүйесінің алғашқы мысалы сызықтық жүйе болды, өйткені екі теңдеу де сызықтарды көрсетеді. Бірақ теңдеулердің сызықтық болуы міндетті емес. Теңдеулер жүйесінің көптеген түрлері бар. Оларға квадрат теңдеулер, көрсеткіштік теңдеулер және логарифмдік теңдеулер сияқты теңдеулердің әртүрлі түрлері кіруі мүмкін. Жүйе ішіндегі теңдеулер бір типті теңдеу болуы міндетті емес. Мысалы, жүйе сызықтық теңдеуді және көрсеткіштік теңдеуді қамтуы мүмкін. Немесе ол логарифмдік теңдеуді және квадрат теңдеуді қамтуы мүмкін. Ол тіпті осы теңдеулердің әрбір түрінің біреуін қамтуы мүмкін, егер әрбір теңдеу бірдей айнымалылар жиынын пайдаланса. Алгебралық жүйе үш ықтимал жолдың кез келгенімен әрекет ете алады:

Жүйеде шексіз көп шешімдер бар.

Жүйенің бірегей шешімі бар.

Жүйеде шешім жоқ.

Екі айнымалы (x және y) бар жүйе үшін әрбір сызықтық теңдеу xy-жазықтықтағы түзуді анықтайды. Сызықтық жүйенің шешімі барлық теңдеулерді қанағаттандыру керек болғандықтан, шешімдер жиыны осы түзулердің қиылысуы болып табылады, демек, не түзу, бір нүкте немесе бос жиын болады.

Үш айнымалы үшін әрбір сызықтық теңдеу үш өлшемді кеңістіктегі жазықтықты анықтайды, ал шешім жиыны осы жазықтықтардың қиылысуы болып табылады. Осылайша, шешім жиыны жазықтық, түзу, бір нүкте немесе бос жиын болуы мүмкін. Мысалы, үш параллель жазықтықтың ортақ нүктесі болмағандықтан, олардың теңдеулерінің шешімдер жиыны бос; нүктеде қиылысатын үш жазықтықтың теңдеулерінің шешімдер жиыны бір нүкте; екі нүкте арқылы үш жазықтық өтетін болса, олардың теңдеулерінің кемінде екі ортақ шешімі болады; шын мәнінде шешім жиыны шексіз және осы нүктелер арқылы өтетін барлық түзуден тұрады. n айнымалы үшін әрбір сызықтық теңдеу n өлшемді кеңістіктегі гипержазықтықты анықтайды. Шешім жиыны осы гипержазықтықтардың қиылысы болып табылады және жазық болып табылады, оның кез келген өлшемі n-ден төмен болуы мүмкін . . . [3]

Жүйенің бірегей шешімі болуы үшін теңдеулер саны белгісіздер санына тең болуы керек. Сонда да шешімге кепілдік берілмейді. Егер шешім бар болса, жүйе дәйекті; шешім болмаса, ол сәйкес емес. Сызықтық теңдеулер жүйесін элементтері теңдеулердің коэффициенттері болатын матрица арқылы көрсетуге болады. Екі белгісіздегі екі теңдеудің қарапайым жүйелерін ауыстыру арқылы шешуге бол, үлкенірек жүйелер матрицалық әдістермен жақсы өңделеді. Алгебралық теңдеуді екі өрнек бір-біріне тең болатын математикалық мәлімдеме ретінде анықтауға болады. Алгебралық теңдеу әдетте айнымалыдан, коэффициенттерден және тұрақтылардан тұрады. Теңдеулер тепе-теңдік таразысына ұқсайды. Егер сіз тепе-теңдік таразысын көрген болсаңыз, таразы «теңдестірілген» деп есептелуі үшін екі жағына бірдей салмақ салу керек екенін білесіз. Бір жағына салмақ қоссақ, таразы бір жағына ауып, екі жағы тепе-теңдікте болмайды. Теңдеулер бірдей логикаға сәйкес келеді. Теңдік белгісінің бір жағында не болса да, екінші жағында бірдей мән болуы керек, әйтпесе ол теңсіздікке айналады.

Енді үш айнмалсы бар теңдеулер жұйесіне келер болсақ, x, y, z үш айнымалыдағы үш теңдеулер жүйесі болып табылады. Сызықтық жүйенің шешімі - барлық теңдеулер бір уақытта орындалатындай айнымалыларға мәндердің тағайындалуы.

Сызықтық жүйенің шешімі деп $_{}_{}_{}$ айнымалыларға теңдеулердің әрқайсысы орындалатындай мәндерді беруді айтады. Барлық мүмкін болатын шешімдер жиыны шешімдер жиыны деп аталады

Дифференциалдық теңдеу, бір немесе бірнеше туындыны қамтитын математикалық тұжырым, яғни үздіксіз өзгеретін шамалардың өзгеру жылдамдығын білдіретін терминдер. Дифференциалдық теңдеулер ғылым мен техникада, сондай-ақ сандық зерттеудің көптеген басқа салаларында өте кең таралған, өйткені өзгерістерге ұшыраған жүйелер үшін тікелей бақыланатын және өлшенетін нәрсе олардың өзгеру жылдамдығы болып табылады. Дифференциалдық теңдеудің шешімі, жалпы алғанда, бір айнымалының бір немесе бірнеше басқаларына функционалдық тәуелділігін өрнектейтін теңдеу; ол әдетте бастапқы дифференциалдық теңдеуде жоқ тұрақты мүшелерден тұрады. Мұны айтудың тағы бір тәсілі - дифференциалдық теңдеудің шешімі, ең болмағанда, белгілі бір шектеулер шегінде бастапқы жүйенің әрекетін болжауға болатын функцияны шығарады.

Дифференциалдық теңдеулер бірнеше кең категорияларға жіктеледі және олар өз кезегінде көптеген ішкі санаттарға бөлінеді. Ең маңызды категориялар қарапайым дифференциалдық теңдеулер және дербес дифференциалдық теңдеулер. Теңдеуге қатысатын функция тек бір айнымалыға тәуелді болса, оның туындылары кәдімгі туындылар болады және дифференциалдық теңдеу кәдімгі дифференциалдық теңдеу ретінде жіктеледі. Екінші жағынан, егер функция бірнеше тәуелсіз айнымалыларға тәуелді болса, оның туындылары жеке туындылар болатындай болса, дифференциалдық теңдеу ішінара дифференциалдық теңдеу ретінде жіктеледі. . [4]

Мысалы, функциясы мен тәуелсіз айнымалысы y және x арқылы белгіленетін қарапайым дифференциалдық теңдеу іс жүзінде у-ның х функциясы ретіндегі маңызды сипаттамаларының жасырын жиыны болып табылады. Егер y үшін айқын формула шығарылса, бұл сипаттамалар талдауға қол жетімді болар еді. Мұндай формула немесе ең болмағанда дифференциалдық теңдеуден шығарылатын x және y теңдеулері (туындылары жоқ) дифференциалдық теңдеудің шешімі деп аталады. Алгебра мен есептеудің қосымшалары арқылы теңдеуден шешімді шығару процесі теңдеуді шешу немесе интегралдау деп аталады. Алайда, анық шешілетін дифференциалдық теңдеулер шағын азшылықты құрайтынын атап өткен жөн. Осылайша, функциялардың көпшілігі жанама әдістермен зерттелуі керек. Тексеру үшін шығаруға мүмкіндік болмаған кезде де оның бар екендігі дәлелденуі керек. Практикада пайдалы жуық шешімдерді алу үшін компьютерлерді қамтитын сандық талдау әдістері қолданылады. Дискриминант, математикада оны жіктеуге немесе шешуге көмек ретінде есептелген объект немесе жүйенің параметрі. ax ² + bx + c = 0, квадрат теңдеу жағдайында дискриминант b ² − 4 ac ; x ³ + ax ² + bx + c = 0 текше теңдеу үшін дискриминант a ² b ² + 18 abc − 4 b ³ − 4 a ³ c − 27 c ² Нақты коэффициенттері бар квадрат немесе текше теңдеудің түбірлері дискриминант оң болса, нақты және анық болады, дискриминант нөлге тең болса, кем дегенде екеуі тең нақты болады және дискриминант теріс болса, күрделі түбірлердің конъюгаттық жұбын қамтиды. Дискриминантты жалпы квадраттық немесе конустық теңдеу үшін табуға болады ax ² + bxy + cy ² + dx + ey + f = 0 ол көрсетілген конустың эллипс, гипербола немесе парабола екенін көрсетеді. Дискриминанттар эллиптикалық қисықтар, шекті өріс кеңейтулері, квадраттық пішіндер және басқа математикалық нысандар үшін де анықталған. Дифференциалдық теңдеулердің дискриминанттары бастапқы теңдеулердің шешімдерінің отбасылары туралы ақпаратты ашатын алгебралық теңдеулер болып табылады. . [5]

1, 3 алгебралық теңдеулер жүйесін шешімділігі :

теңдеулер жүйесін шешудің ең қарапайым әдісі айнымалыларды бірнеше рет жою болып табылады. Бұл әдісті келесідей сипаттауға болады:қарапайым алгебралық теңдеулер жүйелерді шешудің 4 негізгі әдісі бар:

1. Алмастру тәсілі

2. Алгебралық әдістер тәсілі

3. Көбейткіштерге жіктеу тәсілі

4. Жаңа айнмалы енгізу тәсілі

1. Алмастру тәсілі

Алмастыру әдісінде екі айнымалы болады, бір айнмалны екіншы айнмалы арқылы өрнектеп аламыз және сол өрнектеген айнымалымызды екінші айнымалнің орнына қойямыз. мысалы:

$$\left\{ \begin{array}{r} ^{}^{} \\ \end{array} \right. \$$

Осы теңдеуде x- ты y арқлы немесе y-ты x арқылы өрнектеп аламыз сол арқылы есеп оңайласып орнынна қойу арқылы шығарамыз.

2. Алгебралық әдістер тәсілі

Алгебралық әдіс- тәсіл деп жүйедегі айнмалыларды алгебрадағы формулларға әкелу мысалы квадраттар айнмалысынің формуласына және өрнекпен ауыстыру арқылы толығымен жою болып табылады. Бұл мақсат бір теңдеудегі бір айнымалыны шешу және оны басқа теңдеуге қосу, алыу, бөлу, көбейту амалдарын қолдану арқылы орындалады мысалы :

$$\left\{ \begin{array}{r} \\ ^{}^{} \end{array} \right. \$$

Осы есепте екіншы теңдеуді $^{}^{}^{}^{}$ сол арқылы бұл есеп оңайласып шығады.

Тағы бір мысал : $\left\{ \begin{array}{r} ^{}^{} \\ ^{}^{} \end{array} \right. \$ осы мысал да екі теңдеуде де $^{}$ бірдей олардің кәфиссенттерін бідей етіп алып $^{}$ теңдеулер жұйесінен жөйямыз одан x айнмалны тауып алып одан x- ты орнынна қойу арқылы y - ты табамыз.

3. Көбейткіштерге жіктеу тәсілі

$\left\{ \begin{array}{r} ^{}^{}^{}^{} \\ ^{}^{}^{}^{} \end{array} \right. \$ осы теңдеуде бірдей көбейткіш

$^{}^{}$ жақшаның сыртына шығарамыз сол арқылы $\left\{ \begin{array}{r} ^{}^{}() \\ ^{}^{}() \end{array} \right. \$ сол арқылы теңдеу оңайласып теңделер жүйесін шығаруға болады.

4. Жаңа айнмалы енгізу тәсілі

Бұл тәсілде дәрежесі улке или біраз күрделі алгебралық теңдеулерду шешуге қолданылады

Мысалы:
$$\left\{ \begin{array}{r} \\ ^{}^{} \end{array} \right. \$$

Осы теңдеулер жүйесіндеx+y=a, xy=b онда теңдеулер жүйесі білай өзгереді $\left\{ \begin{array}{r} \\ ^{} \end{array} \right. \$

Екі теңдеуді бір-бірне қоссақ теңдеу оңайласады. осы теңдеулер жүйесінен көріп тұрғанымыздай бір теңдеулер жүйесіне 2-3 түрлі тәсіл қолдануға болады. кейде осы 4 түрлі тәсіл бәрі қолдануы да мүмкін.

Ал Көбінесе өте үлкен жүйелер үшін мүлдем басқа тәсіл қолданылады, әйтпесе тым көп уақытты немесе жадты алады. Идея шешімге бастапқы жуықтаудан бастау (бұл мүлде дәл болуы міндетті емес) және оны шынайы шешімге жақындату үшін бұл жуықтауды бірнеше қадаммен өзгерту. Жақындау жеткілікті дәл болғаннан кейін бұл жүйенің шешімі ретінде қабылданады. Бұл итерациялық әдістер класына әкеледі. Кейбір сирек матрицалар үшін кездейсоқтықты енгізу итерациялық әдістердің жылдамдығын жақсартады . . . [6]

1. 3. 1Алгеблалық теңдеулер жүйесін $$ Гаусс $$ әдісімен шешу

Гаусс әдісі-Жүйедегі айнмалыларды түрлендірулер көмегімен біртіндеп жойып, жүйені сатылы түрде келтіріп, айнымалыларды біртіндеп табатын әдіс.

Гаусс түрлендірулері мынандай:

1. кез келген екі теңдеудің орындарын алмастырып жазу

2. кез келген теңдеулердің екі жағын нолден өзге санға көбейту

3. қандай да бір теңдеуді нолден өзге санға көбейтіп, басқа теңдеуге сайкесынше қосу

4, 0=0 түбірдегі теңдеуді сызып тастау

Анықтық үшін үш белгісі бар үш теңдеуден тұратын жүйені қарастырайық( 1. 3. 1 )

$$\left\{ \begin{array}{r} _{}_{}_{}_{}_{}_{}_{}_{}_{} \\ _{}_{}_{}_{}_{}_{}_{}_{}_{} \\ _{}_{}_{}_{}_{}_{}_{}_{}_{} \end{array} \right. \$$

$_{}$ , $_{}$ , болсын, $_{}$ - жетекші элемент деп аталады. осы теңдеулер жүйесінің бірінші теңдеуін $_{}$ - ге мүшелеп бөлеміз:

Сонда $_{}\frac{_{}}{_{}}_{}\frac{_{}}{_{}}_{}\frac{_{}}{_{}}_{}$ = $\frac{_{}}{_{}}$

$_{}$ = $\frac{_{}}{_{}}$ (j $$ ) белгілеуін енгізсек:

$_{}_{}_{}_{}_{}_{}_{}_{}$ (1. 3. 2)

(1. 3. 2) - теңдеуді қолданып ( 1, 2, 1 ) - жүйесінің $_{}$ белгісізін алып тастауға болады ол үшін (1. 3. 2) - теңдеуін алдымен $_{}$ - ге, одан соң $_{}$ көбейтеміз ( 1. 3. 1 ) жүйесінің 2-, 3- теңдеулерін шығару керек.

Нәтижесінде үш теңдеуден тұрақты жүйе аламыз, осы гаусс әдісі арқылы теңдеулер жүйесін шешеу үшін қажетті және жеткілікті шарты - ол жетекшы эелеменіттердің барлығының нөлге тең болуы болып табылады. үшбұрышты матрицаның анықтауышын анықтау үшін коэффициенттерін анықтап алып үшбурыштар әдісі арқылы табу керек

Нақты мысал келтырып көрейік(1. 3. 3)

$$\left\{ \begin{array}{r} {}_{}_{}_{}_{} \\ _{}_{}_{}{}_{} \\ _{}_{}_{}_{} \end{array} \right. \$$

Шешуі: жүйенің кеңейтілегн матрицасын жазып элементар түрлендірулер жасайық

$_{}\frac{_{}}{_{}}\frac{}{}$ =0. 5 ${}_{}\frac{_{}}{_{}}\frac{}{}$ $_{}\frac{_{}}{_{}}\frac{}{}$

Яғни (2) жүйенің бірінші теңдеуін аламыз

$\overset{}{\overbrace{_{}}}$ = $_{}$ - $_{}_{}$ $\overset{}{\overbrace{_{}}}_{}_{}_{}$

$_{}\frac{_{}}{_{}}\frac{}{}$

Осы тәсіл арқыл жаңа теңдеулер жүйесі пайда болады ең соңында $_{}_{}_{}$ Таба аламыз

1, 3, 2 Алгебаралық теңдеулер жүйесін $$ Крамер $$ әдісімен шешу :

$\left\{ \begin{array}{r} _{}_{}_{} \\ _{}_{}_{} \\ _{}_{}_{} \end{array} \right. \$ (1. 3. 4)

Крамер формуласы бойынша : $_{}\frac{_{}}{}_{}\frac{_{}}{}_{}\frac{_{}}{}$

A матриицаның анықтаушын табайық:

A= $\begin{matrix} & & \\ & & \\ & & \end{matrix}$ = 13

Одан ары қарай қарай $_{}_{}_{}$ табу керек
$_{}\begin{matrix} & & \\ & & \\ & & \end{matrix}$ = -13 $_{}\begin{matrix} & & \\ & & \\ & & \end{matrix}$ $_{}\begin{matrix} & & \\ & & \\ & & \end{matrix}$ =39

Енді крамер формуласын

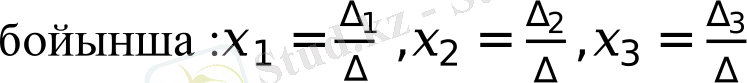
$_{}$ , $_{}_{}$ таба аламыз

1, 3, 3 Алгебаралық теңдеулер жүйесін $$ Зейдель әдісі $$ арқылы шешу

Зейдель әдісінің негізгі идеясы итерациялық процестің әр қадамында $_{}$ -дің

мәндерін есептеу барысында оның алдында есептелген $_{}$ , $_{}$ , …, $_{}$ -1 мәндері

қолданылады да (1. 3. 5) ны ашып жазсақ, Зейдель формуласы келесідей

болады:

$$\begin{pmatrix} _{}\sum_{}^{}_{}_{} & &_{} \\ & & \\ _{}\sum_{}^{}_{}_{} &_{}_{} &_{} \end{pmatrix}$$

итерациялық процесінің жинақтылығы үш метрикалық кеңістікте мына шарттардың бірі орындалуымен бекітіледі:(1. 3. 6)

$_{}() \underset{}{\overset{}{︸}}\left\lfloor_{}_{} \right\rfloor$ кеңістікте

A= $\underset{}{\overset{}{︸}}\sum_{}^{}\left_{} \right$ шарты

Осы шарттар бойынша Егер бұл шарт орындалса, итерациялық процесс кез

келген бастапқы жуықтауда өзінің жалғыз шешіміне жинақталады.

Зейдель әдісін жүйенің матрицасы симметриялы элементтерден тұрған

жағдайда қолданады. Егер матрица симметриялы болмаса оны симметриялы

түрге келтіру үшін жүйенің матрицасын және векторларын транспонирленген

матрицаға көбейтеді:

$^{}$ *А*х=AT

Белгілеулер енгіземіз:

$^{}$ *A=C

$^{}$ *b=D

Сонда Cx=D

(1. 3. 6) - жүйені қалыпты жүйе деп атайды. Қалыпты жүйенің элементтері

симметриялы және диагональды элементтері нөлден өзгеше болады.

1, 3, 4 Алгебаралық теңдеулер жүйесін $$ қуалау әдісі $$ арқылы шешу

Математикалық физиканың есептері көбінде үш диагональді сызықты

алгебралық теңдеулер жүйесінің шешімін табуға шектеледі, үш диагоналді

сызықты алгебралық теңдеулер жүйесінің теңдеулерінде тек қана үш

айнымалылардың коэффициенттері нөлге тең емес, қалған коэффициенттер

нөлге тең.

$_{}_{}_{}_{}_{}_{}_{}$

j =1, 2, 3, …, n-1

$_{}_{}_{}_{}$ , $_{}_{}_{}_{}$

Үш диагоналді сызықты алгебралық теңдеулер жүйесін шешу тиімді

әдісі болып қуалау әдісі табылады.

Қуалау әдісінің бірінші кезеңі - тура қуалау. Қуалау коэффициенттері келесі формулалармен табылады

2, 1 қолданбалы есептердің математикалық моделі

Математиканы оқытудың негізгі мақсаттарына жатады қарапайым нақты құбылыстардың математикалық модельдерін құру, берілген модельдерді пайдалана отырып құбылыстарды зерттеу және қолданбалы дизайн жасау дағдыларын дамыту модельдер. Бұл мақсатқа жету құралдарының бірі математикалық модельдеу әдісі болып табылады. Математикалық модельдеу сөздің тар мағынасында нақты мәндердің теңдеулері мен теңсіздіктері түріндегі сипаттау ретінде түсініледі.

физикалық, химиялық, технологиялық, биологиялық, экономикалық және басқа процестер. Үшін әртүрлі процестерді талдау және синтездеу үшін математикалық әдістерді қолдану, оларды сипаттай білу керек. процестерді математика тілінде, яғни оларды теңдеулер мен теңсіздіктер жүйесі түрінде сипаттау. Модель құрастыру кезінде талдау сияқты ойлау операциялары қолданылады. ғылымнің дамуына ықпал ететін синтез, салыстыру, жіктеу, жалпылау арқылы. Математикалық модель құру және есепті математика тіліне аудару студенттерді нақты процестерді модельдеуге дайындайды және олардың болашақ кәсіби қызметіндегі құбылыстар. [7] Математикалық модельдеу ерекше рөл атқарады экономикалық және ғылыми қызмет саласында. Экономикада көлік есептерін шешуде математикалық модельдеуді қолдануды қарастырайық, сонымен қатар схемалар теориясындағы есептердегі математикалық модель Марков, ықтималдықтар теориясында. Осылайша біз әртүрлі салаларда математикалық модельдеудің маңыздылығын көрсетеміз.

1. Экономикадағы математикалық модельдеу.

Көлік мәселесінің математикалық моделі болып табылады . сызықтық бағдарламалау есебінің математикалық моделі. Шектеу жүйесінің көптеген шешімдерінің арасында мұндай теріс емес шешімді табу керек, қашан онда мақсат функциясы минимумды қабылдайды мағынасы. Кез келген басқа сызықтық бағдарламалау мәселесі сияқты, көлік мәселесін шешуге болады.

симплекс әдісін қолдану. Арнайы құрылғының арқасында

шектеу жүйелері симплекс әдісінің жалпы процедурасы

көлік мәселесіне қолданғанда ол айтарлықтай жеңілдетілген.

... жалғасы

Екінші және үшінші ретті анықтауыштар және олардың қасиеттері. Крамер формуласы

Жалпы түрдегі алгебралық теңдеулер жүйесін шешу жолы

Сызықтық алгебралық теңдеулер жүйесін шешу әдістері

Көрсеткіштік теңдеулерді шешудің әдістері

Логарифмдік теңдеулерді шешу

Теңдеулер жүйесін шешу

Мектепте алгебралық және геометриялық материалдарды қабылдау мен меңгеру ерекшеліктері

Көрсеткіштік теңдеулерді шешудің графиктік әдісі

Анықталмаған интеграл қасиеттері

Теңдеулер мен теңсіздіктер және оларды шығару тәсілдері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс