Анықталмаған интегралды оқыту әдістемесі мен есептеу әдістері


«Математика және ақпараттық технологиялар» кафедрасы«Бизнес, техника және технология» жоғары мектебі
КУРСТЫҚ ЖҰМЫС
Пәннің коды, атауы: 6В01503-Математика
Тақырыбы:Анықталмаған интегралды оқыту әдістемесі
Ғылыми жетекшісі: п. ғ. к., доцент Серікбаева Валентина Ержанқызы
Орындаған: МАТ-23/2-1 Моңкебаев Қайрат Бекенұлы
Курс жұмысы қорғалды « » 2023ж.
(бағасы)
Комиссия төрағасы
(қолы)
Мазмұны
Kipicпe
Анықталмаған интегралды есептеудің тәжірибеде ыңғайлы жалпы әдістерінің жоқтығына байланысты және есептеудің оқушылар үшін жеткілікті деңгейде күрделілігіне байланысты әр дайым есептеуде жиі кездесетін функциялардың кейбір дербес кластарының интегралдау әдістерін қарастыруға тура келеді.
Математиканы оқыту әдістемесі ең алдымен төменгі класс оқушыларына математиканы оқыту міндетін жалпы оқу және тәрбие жүйесімен бірге қарастырады. Әдістемеде математиканың бастауыш курсының мазмұны мен құрылысы ашылып айқындалынады, яғни математикадан бастауыш кластарда қандай материал оқылатыны және неге дәл сол материал таңдап алынғандығы, курстың әрбір жеке мәселесі бастауыш кластарда қандай дәрежеде жинақталып оқылатыны, курс тақырыптары қандай тәртіпте қарастырылатыны және мұндай тәртіптің неге анағұрлым тиімді екендігі айтылады.
Математикалық анализді кластарда оқыту әдістемесінде курстағы әрбір тараудын, және сол тараудағы әр мәселені мысалы, интегралдарды табу қосу мен азайтуды қалай оқып үйрену керектігі, атап айтқанда, осы тақырыпта қосудың ауыстырымдылық қасиетін анықтау оқып үйренудін дербес әдістері айқындалады. Математиканы оқыту әдістемесі оқушыларға теориялық білімді игеру, алған білімін алуан түрлі практикалық мәселелерді шешу үшін қолдана білуге үйрену, оқушыларда берік дағды қалыптастыру жөнінде дәлелді ақыл-кеңестер ұсынады.
Курстық жұмыстың мақсаты: Математиканы оқытуда есептердің алатын орны ерекше. Оны оқытудың негізгі мақсаты - математикалық есептердің белгілі бір жүйесін шешу. Әдістемесін игеру. Сондықтан есепті шешу - оқытудың мақсаты ғана емес, сондай - ақ құралы да. Оның қатарына пәнді оқытуда қарастырылатын әр алуан жаттығулар, мысалдар, логикалық тапсырмалар, яғни кез келген математикалық мазмұнды тапсырманы жатқызуға болады. Есепті шешу кезінде оның шартына немесе салдарына математикалық жалпы қағидаларды қолданудың реті анықталады.
Курстық жұмыстың міндеті:
- Анықталмаған интеграл және оның қасиеттері ;
- Анықталмаған интегралдарды есептеу әдістері;
- Тәжірибелік-эксперименттік жұмыс
Курстық жұмыстың зерттеу обьектісі . Математикалық анализ.
1 Интеграл туралы жалпы ұғым
Интеграл (лат. Іnteger - бүтін) - математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады.
«Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған;
- өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама (1-сурет) .
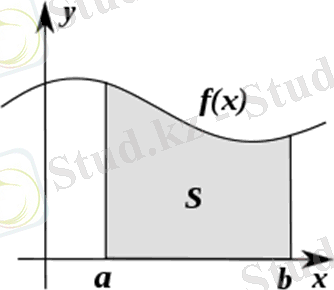
1-сурет - Анықталмаған интеграл
Анықталмаған интегралды іздеу амалы немесе дифференциалдық теңдеулерді шешу.
Осыған сай дифференциалдау формулалары мен ережелеріне сүйене отырып, интегралдаудың формулалары мен ережелерін алуға болады.
1. 1 Анықталмаған интеграл
Егер
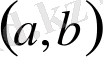 интервалының кез келген
х
берілген нүктесінде
интервалының кез келген
х
берілген нүктесінде
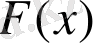 функциясы дифференциалданатын болса және оның туындысы
функциясы дифференциалданатын болса және оның туындысы
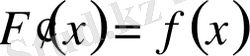 болса, онда
болса, онда
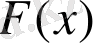 фукнциясы
фукнциясы
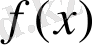 функциясының алғашқы функциясы деп аталады.
функциясының алғашқы функциясы деп аталады.
Мысал:
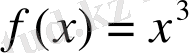 функциясының алғашқы функциясын табу керек.
функциясының алғашқы функциясын табу керек.
Шешуі
Алғашқы функцияның анықтамасы бойынша
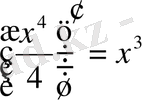 болғандықтан,
болғандықтан,
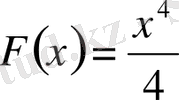 функциясы
функциясы
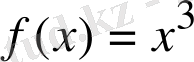 -тің алғашқы функциясы болады.
-тің алғашқы функциясы болады.
Теорема:
Егер
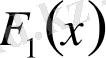 және
және
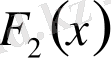
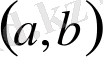 интервалында берілген
интервалында берілген
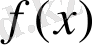 функциясының кез келген алғашқы функциялары болса, онда берілген интервалда
функциясының кез келген алғашқы функциялары болса, онда берілген интервалда
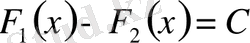 теңдігі орындалады, мұнда С-қайсы бір тұрақты. Демек, бір функцияның кезкелген алғашқы функциялары тек тұрақты шамаға ғана айрықшаланады. Алдындағы көрсетілген есепте алғашқы
теңдігі орындалады, мұнда С-қайсы бір тұрақты. Демек, бір функцияның кезкелген алғашқы функциялары тек тұрақты шамаға ғана айрықшаланады. Алдындағы көрсетілген есепте алғашқы
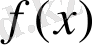 функциялары деп мына функцияларды алуға болады:
функциялары деп мына функцияларды алуға болады:
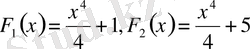 . Немесе жалпы түрде
. Немесе жалпы түрде
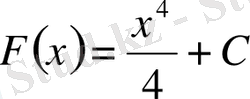 , мұнда С-
, мұнда С-
кезкелген тұрақты, өйткені
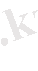
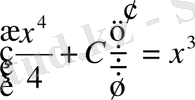 .
.
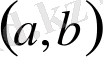 интервалында берілген
интервалында берілген
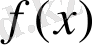 функциясының
функциясының
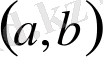 интервалында берілген барлық алғашқы функциялар жиынын анықталмаған интеграл деп атап, былай белгілейді:
интервалында берілген барлық алғашқы функциялар жиынын анықталмаған интеграл деп атап, былай белгілейді:
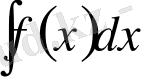
Мына белгілеуде
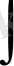 -интеграл белгісі,
-интеграл белгісі,
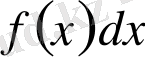 - интеграл астындағы өрнек,
- интеграл астындағы өрнек,
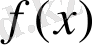 - интеграл астындағы функция,
- интеграл астындағы функция,
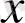 -интегралдау айнымалысы.
-интегралдау айнымалысы.
Егер
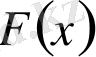 функциясы
функциясы
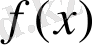 функциясының бір алғашқы функциясы болса, яғни,
функциясының бір алғашқы функциясы болса, яғни,
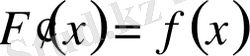 , онда
, онда
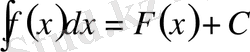 , мұнда С-кезкелген тұрақты (1)
, мұнда С-кезкелген тұрақты (1)
Интеграл астындағы
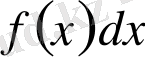 өрнек теңдіктің оң жақтағы кез келген алғашқы функцияларының дифференциалы болады.
өрнек теңдіктің оң жақтағы кез келген алғашқы функцияларының дифференциалы болады.
Берілген интеграл астындағы функция бойынша анықталмаған интегралды табу интегралдау амалы деп аталады. Дифференциалдау амалына қарағанда интегралдау қарама-қарсы амал. Анықталмаған интегралдың геометриялық мәні:
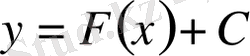 , С- параметр, қисықтар жиыны. Осы жиынға жататын қисықтар интегралдау қисықтары деп аталады. Осы жиынның кез келген қисығын Оу осінің бойымен параллель жылжытып алуға болады.
, С- параметр, қисықтар жиыны. Осы жиынға жататын қисықтар интегралдау қисықтары деп аталады. Осы жиынның кез келген қисығын Оу осінің бойымен параллель жылжытып алуға болады.
1. 2 Анықталмаған интеграл, оның қасиеттері
F(x) функциясы дифференциалдау деп берілген алғашқы F(x) функциясының F’(x) = f(x) туындысын немесе df(x) =f(x) dx.
Дифференциалын табу амалын айтамыз.
Сол амалға кері амал, яғни F’(x) болып табылатын берілген f(x) үшін алғашқы F(x) функциясын табу амалы f(x) - ті интегралдау деп аталады .
F (x) - ті интегралдау амалын көрсету үшін ʃ символы қолданылады да, былай жазылады: ʃ f(x) dx.
Осы ʃ f(x) dx берілген f(x) функциясының барлық алғашқы функцияларының жиынын бейнелейді және f(x) - тен анықталмаған интеграл деп аталады.
Демек, анықтамаға сәйкес ʃ f(x) dx = F(x) + C болады. Бұл формуладағы F(x) функциясы f(x) - тың белгілі бір алғашқы функциясы, С -кез келген тұрақты.
Сонымен бірге f(x) - интеграл астындағы функция, ал f(x) dx - интеграл астындағы өрнек деп аталады.
ʃ - символы ұзартылып алынған латын алфавитіндегі S әріпі, ол символды интегралдың белгісі деп атайды.
Функцияны интегралдау және олардың алғашқы функцияларының қаиеттері жайындағы ілім интегралдық есептеу деп аталады.
Дифференциалдық есептеу сияқты интегралдық есептеуде математикалық анализдің өте маңызды бөлімдерінің бірі болып табылды. қарастырылған есептердің шешуін енді интеграл түрінде былай жазуға болады:
S = fv(t) dt + C
m = fp(t) dt + C.
Теорема-1 . Екі және бірнеше функцияның алгебралық қосындысының анықталмаған интегралы олардың интегралдарының қосындысына тең.
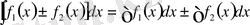 .
.
Теорема-2.
Тұрақты көбейткішті интеграл таңбасының алдына шығаруға болады, яғни егер а - тұрақты сан болса,
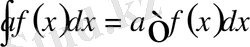 болады.
болады.
F’(x) =f(x) және екенін ʃ f(x) dx = F(x) + C ескере отырып анықталмаған интегралдың қасиеттерін қарастырамыз.
1) Дифференциалдың анықталмаған интегралы дифференциалданған функция мен кез келген тұрақтының қосындысына тең, яғни:
ʃ df(x) dx = F(x) + C
2) Анықталмаған интегралдың дифференциалын интеграл астындағы өрнекке тең, яғни:
dʃ f(x) dx = f(x) dx
3) Тұрақты көбейткішті интегралдық белгінің алдына шығаруға да, интегралдық белгінің астына алып баруға да болады, яғни:
ʃ kf(x) dx = kf(x) dx
2 Анықталмаған интегралдың негізгі кестесі
1-Анықтама.
Егер [a, b] кесіндісінің кез келген нүктесінде
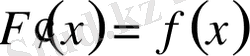 болса, онда F(x) функциясы f(x) функциясының алғашқы функциясы деп аталады.
болса, онда F(x) функциясы f(x) функциясының алғашқы функциясы деп аталады.
Мысалы:
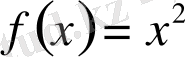 функциясының алғашқы функциясы
функциясының алғашқы функциясы
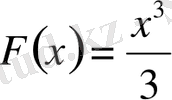 болады, өйткені
болады, өйткені
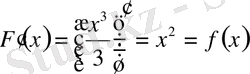 болады.
болады.
Теорема-1.
Егер
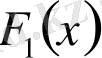 және
және
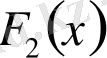 функциялары f(x) функциясының [a, b] кесіндісіндегі екі алғашқы функциялары болса, онда олардың айырмасы тұрақты сан болады.
функциялары f(x) функциясының [a, b] кесіндісіндегі екі алғашқы функциялары болса, онда олардың айырмасы тұрақты сан болады.
2-Анықтама
. Егер
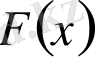 функциясы f(x) -тің алғашқы функциясы болса, онда
функциясы f(x) -тің алғашқы функциясы болса, онда
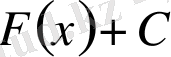 өрнегі f(x) функциясының анықталмаған интегралы деп аталады. және
өрнегі f(x) функциясының анықталмаған интегралы деп аталады. және
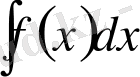 деген белгімен белгіленеді. Сонымен
деген белгімен белгіленеді. Сонымен
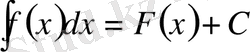 болады. Мұндағы
болады. Мұндағы
f(x) интеграл астындағы функция деп, f(x) dx интеграл астындағы өрнек деп аталады. х интегралдау айнымалысы деп, ал белгі
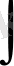 -анықталмаған интегралдың таңбасы деп аталады.
-анықталмаған интегралдың таңбасы деп аталады.
Теорема-2. Берілген сегментте үздіксіз кез келген функцияның осы сегментте алғашқы функциясы болады. Берілген функцияның анықталмаған интегралын табу амалы сол функцияны интегралдау деп аталады.
Интегралдауды жеңілдету үшін негізгі интегралдардың таблицасы беріледі. Бұл таблицалардың дұрыстығын дифференциалдау арқылы жеңіл тексеруге болады.
1.
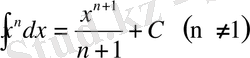
2.
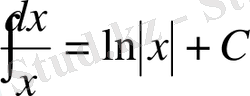
3.
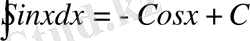
4.
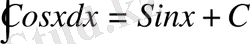
5.
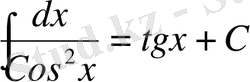
6.
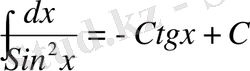
7.
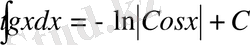
8.
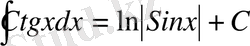
9.
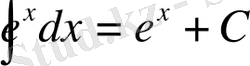
10.
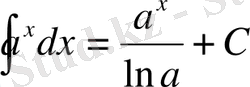
11.
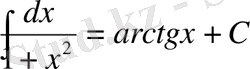
11*.
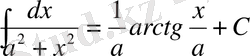
12.
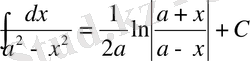
12*.
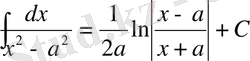
13.
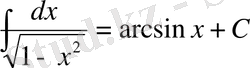
13*.
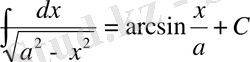
14.
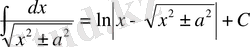
15.
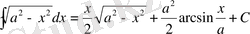
16.
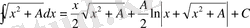
2. 1 Анықталмаған интегралдарды есептеу әдістері
Интегралды интегралдау әдістері интеграл астындағы функцияның берілуіне және интегралдау кестесінің қорына байланысты:
- тікелей интегралдау;
- айнымалыларды ауыстыру арқылы интегралдау;
- бөліктеп интегралдау.
Осы тәсілдерді жеке қарастырайық:
Тікелей интегралдау әдісі.
Функцияларды анықталмаған интегралдың қасиеттері мен интегралдар кестесіне сүйеніп тікелей интегралдауға болады. Ал, тригонометриялық фнкцияларды интегралдағанда қосымша келесі келтіру формулаларын пайдалануға болады:
- sin²x+cos²x=1, sinx=
- ctgx=, tgx*ctgx=1
- cosec, secx=
- sin2x=2sinx*cosx, cos2x=cos²x-sin²x=2cos²x-1=1-2sin²x
- sinx*cosy=
cosx* siny = (sin (x+y) -sin (x-y) ) cos*cosy = (cos(x+y) +cos(x-y) ) sinx*siny = (cos(x+y) -cos(x-y) ) .
Мысал, ∫ интегралын есептеп, нәтижесін дифференциалдау арқылы тексеріңдер. Алымын бөліміне бөліп, интегралдың қасиетін және кестені пайдаланып, шығарамыз:
1. ∫-1/4dx-2∫ x15/4dx+∫ x5/12dx=4x3/4-x19/4+ x17/12+C=4-19+12√x17+C.
- ∫ cos7xdx
- ∫sin(2x-6) dx
- ∫ sin²xdx
Интеграл астындағы функцияның бөліміндегі өрнектен толық квадратты бөліп аламыз. Сонда 1. ∫ =∫ = =4√3/6√13arctg
- ∫dx
Алымында бөлімінің туындысына тең болатын қосылғышты айырып алып, алатынымыз:
∫=∫(4-8x) -2/5dx=-(4-8x) 3/5+C=-⁵√(4-8x) ³+C5. ∫6. ∫dx7. ∫dx= ∫dx= ∫=dx= ∫(1-cosx) dx=x-sinx+C
Негізгі интегралдар кестесін қолданып, анықталмаған интегралдар қасиеттерін пайдаланып интеграл астындағы өрнекті түрлендіріп интегралдағанды тікелей интегралдау деп атайды.
№1 Интегралдарды табу керек.
а)
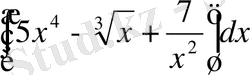 , б)
, б)
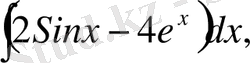
в)
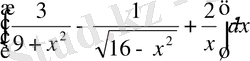
Шешуі:
1) Алдымен интеграл астындағы функцияны ықшамдап, сосын анықталмаған интеграл қасиеттерін және (1) кестелік интегралды қолданып есептейміз.
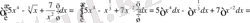
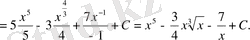
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz