Дифференциалды оқыту кезінде математикалық есептерді шешуге оқыту әдістемесі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 73 бет
Таңдаулыға:

ТӨЛЕПБЕРГЕН СЫМБАТ ҚАРЖАУБАЙҚЫЗЫ
Мектеп математика курсында мәтінді есептерді оқыту әдістемесін жетілдіру жолдары

Ғылыми жетекшісі:
Нурбаева Д.М., PhD, аға оқытушы

МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..4
1 МӘТІНДІ ЕСЕПТЕРДІ ШЕШУДЕ ОҚУ ІС-ӘРЕКЕТІНІҢ ӘДІСТЕРІН ҚАЛЫПТАСТЫРУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
1.1 Мәтінді есеп түсінігі. Мәтінді есеп құрылымы. Мәтінді есептердің классификациясы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .10
1.2 Оқу іс-әрекетін қалыптастырудағы мәтінді есептердің маңыздылығы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...24
2 МЕКТЕП МАТЕМАТИКА КУРСЫНДА МӘТІНДІ ЕСЕПТЕРДІ ШЕШУ ТӘСІЛДЕРІН ҚАЛЫПТАСТЫРУДЫҢ ӘДІСТЕМЕЛІК НЕГІЗДЕРІ
2.1 Мәтінді есептерді шығаруға үйрету әдістемесі ... ... ... ... ... ... . ... ... ... ... ... .32
2.2 Оқушылардың функционалдық сауаттылығын арттыруға бағытталған мәтінді есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .63
ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 77
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... . ... ... ... ... ... ... ... .78

НОРМАТИВТІК СІЛТЕМЕЛЕР
Бұл диссертацияда келесі стандарттардың сілтемелері қолданылған:
1. Қазақстан Республикасының 2007 жылғы 27 шілдедегі №319 Білім туралы Заңы (ҚР 04.07.2018 №171-VI өзгертулер мен толықтырулар енгізілген).
2. Қазақстан Республикасы Орта білім берудің (бастауыш, негізгі орта, жалпы орта білім беру) мемлекеттік жалпыға міндетті стандарты Қазақстан Республикасы Үкіметінің 2012 жылғы 23 тамыздағы №1080 Қаулысымен бекітілген.
3. Қазақстан Республикасында білім беруді және ғылымды дамытудың 2016-2019 жылдарға арналған мемлекеттік бағдарламасы Қазақстан Республикасы Үкіметінің 2018 жылғы 24 шілдедегі №460 Қаулысымен бекітілген.
4. Білім берудің барлық деңгейінің мемлекеттік жалпыға міндетті білім беру стандарттарын бекіту туралы Қазақстан Республикасы Білім және ғылым министрінің 2018 жылғы 31 қазандағы №604 бұйрығы.

КІРІСПЕ
Зерттеу жұмысының өзектілігі: Жай айту - үйрету дегенді білдірмейді, жай тыңдау - үйрену дегенді білдірмейді. Кейбір оқу процесі мұғалімнің айналасында жүреді, онда студенттер тек пассивті ақпарат алады. Оқушыларға бағытталған оқу процесінде мұғалім тек оқушылар арасындағы байланысты нығайтатын, жақсартатын маман немесе бағыттаушы болып табылады, ол қазіргі заманғы білім беру жүйелерінің басты бағыты.
Адамдар өз өмірлерінде көп қиындықтарға тап болады және олар осы қиындықтарды өздерінің білімі мен тәжірибесіне байланысты белгілі бір жолмен шешуге тырысады. Осыған байланысты оқушылардың болашақ немесе жақын болашақтағы қиындықтарға дайын болуы, олардың оқу ортасында нағыз өмірлік немесе ұқсас қиындықтарға тап болуы және осы мәселелердің тиісті шешімін таба білуі маңызды. Әрбір қоғам өзінің білім беру жүйесінен адамдарға олардың өміріндегі мәселелерді тиімді шешуге мүмкіндік береді деп күтеді. 21 ғасырдың оқушысы ретінде оқушылар сыни ойшылдар мен кез-келген қиындықтарды шешушілер болуы керек. Егер сіз адамға балық аулауды үйретсеңіз, ол өмір бойы балық аулай алады. Сол сияқты, егер сіз оқушыға мәтінді есептерді шешуге үйретсеңіз, ол оны өмір бойы қолдана алады.
Біз әлеуметтік саяси және технологиялық жағдайлар үнемі өзгеріп отыратын динамикалық қоғамда өмір сүріп жатырмыз, сондықтан мұғалімдер оқушыларды нағыз өмірлік жағдайға дайын ететін тиісті оқу бағдарламалары мен оқыту әдістерін анықтау үшін тенденцияларды талдап, бағалауы керек.
Математика - бұл заңдылық пен логикалық тәртіпке ие, сонымен қатар осы заңдылықты табатын және зерттейтін ғылым.
Математика ғылым мен техниканың негізі болып табылады. Математиканың ғылым мен техникадағы функционалды рөлі әр түрлі, сондықтан ғылымның, техниканың және бизнестің бірде-бір саласы оны қолданудан бас тарта алмайды. Бірақ математика - жалпы білім беретін мектептегі ең нашар оқытылатын, оқушылардың кейбірі жек көретін және нашар түсінілетін пәндердің бірі.
Оқушылардың нашар үлгерімінің себебі қоғамның математика қиын деген пікірі, білікті мұғалімдердің жетіспеушілігі, математикалық зертхананың болмауы және оқыту әдістемесінде тартымдылық пен жаңалықтың болмауы сияқты факторлармен түсіндіріледі. Оқушыға тапсырма бере отырып, оларға тәуекелге баруға, жаңа түсінік қабылдауға, білімді қолдануға, контексте жұмыс істеуге және ашушылардың үрейінен ләззат алуға мүмкіндік беру керек.
Мұғалімнің ең маңызды жетістігі - оқушыларға өз бетінше білім алу жолында көмектесу. Оқушыларға математикалық білімді ұсынумен қатар, мұғалімдер оқушыларды ақпаратты сұрыптауға және олардың білімдерін қолданбалы және өмірлік жағдайларда қолдануға баулуы керек.
Математика бойынша оқушылардың үлгерімінің төмен екендігі туралы дәлелдер математиканы технологиялық, ғылыми және іскери қолданудың тұрақты бола алмайтындығын көрсетеді. Бұл математиканы түсіну мен оқушылардың үлгерімін іс жүзінде жақсартуға бағытталған оқыту стратегиясын іздеуді бірінші орынға қояды. Мәтіндік есептерді оқыту әдісі ретінде шешу негізгі фактілерді, ұғымдар мен процедураларды, сондай-ақ проблемаларды шешудің мақсаттарын үйренудің тәрбиелік рөлін орындау үшін қолданыла алады.
Мәтіндік есептерді шешу - бұл көптеген қолданбалылығы бар математиканың негізгі бөлігі және көбінесе бұл қолданба математикадағы маңызды мәселелерді ұсынады. Жалпы білім беретін мектептерде математикадан мәтіндік есептерді шешу оқушылардың қызығушылығы мен ынтасын оятады.
Психологтар мен педагогтардың (А. Е.Леонтьев, А. Б.Брушлинский, Е. Х. Кабанова-Меллер, П. Я. Халперин, Н. Ф. Талызин және т. б.) еңбектерінде есеп ұғымы, оның компоненттері, олардың қасиеттері мен өзара әрекеттесу шарттары кеңінен зерттеледі.
В. Н.Эпифания, Е. Х. Кабанова-Меллер, З. И. Калмыкова, В. И. Решетников, Х. А. Менчинская, Л. О. Гурова, А. Б. Петровский сияқты психологтардың мәтінді есептерді шешуге оқыту мәселелері бойынша зерттеулері білім алушылардың оқу іс-әрекетінің әдістерін қалыптастыру процесінде белсенді қызметін қамтамасыз ететін әдістемені әзірлеу қажеттілігін көрсетеді.
Есептерді шешуге оқыту әдістемесін жетілдіру, математиканы оқытудағы есептердің рөлі мен орнын анықтау мәселелері Д.В. Клименченко, Ю. М. Колягин, Д. Поя, Л. М. Фридман, п. м. Эрдниевтің жұмыстарында қойылады. Бұл зерттеулерде міндеттерді жіктеу және жүйелеу тапсырмалардың сыртқы құрылымы туралы білімді ескере отырып жүзеге асырылады.
Есепті күрделі объект ретінде зерттеумен, оның сыртқы және ішкі құрылымымен байланысты мәселе В.И. Крупичтің жұмысына арналған. Есепті оның құрылымы тұрғысынан зерттеу оқушылардың оқу іс-әрекетінің әдістерін қалыптастыруға бағытталған мәтіндік алгебралық есептер жүйесін құруға мүмкіндік береді.
Қазақстанда математикалық бiлiм берудi дамытумен оқушылардың ойлау ic-әрекетiн жандандыру және математиканы оқыту әдiстемесiнiң теориялық негiзi болатын есептердi шығаруды окытудың мәселелерi белгiлi ғалым- әдiскерлер А.Е. Әбілкасымова, Б.Б.Баймұханов, М.Е.Есмұхан, Ә.К.Қағазбаева, А. М.Мүбараков, Л.У.Жадраева, Е.Ж.Смағұлов, Л.Т.Искакованың және т.б. енбектерiнде қарастырылған.
Математиканы оқытудың негізгі мақсаты - оқушыларға күнделікті өмірдегі мәселелерді шешуге мүмкіндік беру. Өкінішке орай, Ұлттық біріңғай тесттердің соңғы нәтижелері бойынша оқушылардың көпшілігінде математикалық есептерді шешу дағдылары жоқ екендігі көрінеді. Бұл математикадағы жалпы жетістіктердің төмен болып саналуының бір себебі болып табылады. Бұл сонымен қатар оқушылардың мәтіндік есептерді түсіну қиын екенін, оларды шешу процесіне әсер ететінін көрсетеді. Сондықтан мұғалімдер оқушылардың оқу процесіне сәйкес келетін дұрыс оқу жоспарын құра алуы үшін бұл зерттеу оқушылардың математикалық есептерді шешудегі қиындықтарды талдауға бағытталған.
Зерттеу мәселесі: Мектеп математика курсында мектеп оқушыларының мәтіндік есептерді шешуге оқытудың теориялық және әдістемелік негіздемесі
Зерттеу жұмысының мақсаты: Мектеп математика курсында оқушылардың мәтіндік есептерді шешуге үйретуде тиімді, әрі табысты әдістерді дамыту. Мәтіндік есептердің қалыптасуы мен дамуының әдіснамасын жетілдіру және оны жалпы білім беретін мектептің оқушыларында қолдану.
Зерттеу нысаны: Мектеп математика курсында мәтіндік есептерді шешуге оқыту процесі.
Зерттеу пәні: Мектеп математика курсында мәтіндік есептерді шешуге оқыту әдістемесі.
Зepттeyдiң ғылыми бoлжaмы - егер жүйе ретінде Есеп және есепті шешу ұғымдарының мәнін, есептерді шешудің функциялары мен есептерді шешу дағдыларын қалыптастыруға бағытталған есептер жүйесін құру принциптерін, сондай-ақ есептерді шешудің жалпыланған әдісін қалыптастыру кезінде оқытуды саралауды жүзеге асыру жолдарын анықтау негізінде мәтіндік есептерді шешуге оқыту әдістемесі әзірленетін болса, онда оқушылардың есептерді шешуге арналған дағдыларының қалыптасу деңгейі артады, өйткені бұл жағдайда оқушылардың есептерді шешудегі әрекеттері саналы болады, олардың есептерді шешуге қызығушылығы артады.
Зepттey мaқcaты, пәнi мeн бoлжaмғa cәйкec кeлeci мiндeттep қoйылды:
1. Есеп және есепті шешу ұғымдарының мәнін жүйе ретінде анықтау негізінде есептерді шешу функциялары мен сараланған оқыту жағдайында мәселелерді шешу дағдыларын қалыптастыруға бағытталған міндеттер жүйесін құру принциптерін ашу.
2. Есептерді шешудің жалпыланған әдісін қалыптастыру кезінде оқытуды саралауды жүзеге асыру жолдарын және сараланған оқыту жағдайында математикалық есептерді шешу бойынша оқушылардың оқу іс-әрекетін ұйымдастыру тәсілдерін анықтау.
3. Сараланған оқу процесі жағдайында математикалық есептерді шешуге оқыту әдістемесін жасау және оның тиімділігін тәжірибелік-эксперименттік жолмен тексеру.
Зерттеу көздері: математикалық білім беру саласындағы заңнамалық және нормативтік құжаттар, отандық және шетелдік зерттеушілердің ғылыми еңбектері, оқу-әдістемелік әдебиет, қоғамдық-саяси әдебиет және психологиялық-педагогикалық мерзімді басылымдар. Зерттеу "білім туралы заңда", республиканың үкіметтік құжаттарында көрсетілген орта мектепке қоғамның қазіргі заманғы талаптары негізінде жүзеге асырылды.
Зepттey әдicтepi:
-зерттеу тақырыбы бойынша психологиялық-педагогикалық, математикалық және әдістемелік әдебиеттерді талдау;
- мектеп практикасындағы зерттелетін проблеманың жағдайын зерделеу және талдау (Математиканы оқыту процесін бақылау, мұғалімдер мен оқушыларға сауалнама жүргізу, мектеп бағдарламаларын, оқулықтар мен оқу құралдарын зерделеу, оқушылардың жазбаша жұмыстарын талдау);
- жүйелік тәсіл әдіснамасы негізінде проблеманы теориялық зерттеу;
- педагогикалық эксперимент және эксперимент нәтижелерін өңдеу.
Зepттeyдiң ғылыми жaңaлығы мeн тeopиялық мaңыздылығы:
1. Есеп және есепті шешу ұғымдарының мәні, мәртебесі жүйелі тәсіл мен қызмет теориясын жүйелі талдау негізінде анықталды және оқу процесінде тапсырманың көп функционалдылығы анықталды, бұл оны ақыл-ой әрекетінің мақсаты, ұғымдарды қалыптастыру және ойлауды дамыту құралы ретінде анықтауға мүмкіндік береді.
2. Жүйелік талдау негізінде есептерді шешу функциялары және сараланған оқыту кезінде мәселелерді шешу дағдыларын қалыптастыруға бағытталған есептер жүйесін құру принциптері анықталды.
3. Есептерді шешудің жалпыланған тәсілін қалыптастыру кезінде оқытуды саралауды жүзеге асыру жолдары және сараланған оқыту жағдайында математикалық есептерді шешу бойынша оқушылардың оқу іс-әрекетін ұйымдастыру тәсілдері анықталды.
4. Сараланған оқытуда математикалық есептерді шешуге оқыту әдістемесі әзірленді.
Зepттey жұмыcының пpaктикaлық мaңыздылығы: диссертацияда әзірленген математикалық есептерді шешуде оқу іс-әрекеті әдістерінің жүйесін қалыптастыру бойынша теориялық ережелер мен практикалық ұсыныстарды математика мұғалімдері өздерінің практикалық қызметінде оқушылардың тиісті білімінің, іскерлігі мен дағдыларының сапасын арттыру үшін қолдана алатындығында. Зерттеу нәтижелерін негізгі мектепте математиканы оқытудың мазмұны мен әдістерін жетілдіруде, сонымен қатар студенттерге, мұғалімдер мен оқушыларға арналған оқу-әдістемелік құралдарды жасауда қолдануға болады.
Қopғayғa ұcынылaтын нeгiзгi қaғидaлap:
1. Негізгі мектептегі математикалық есептерді шешуге оқытудың теориялық негіздері және қызмет теориясын жүйелі талдау және жүйелік тәсіл негізінде анықталған есеп және есепті шешу ұғымдарының сипаттамасы.
2. Оқу процесінде математикалық есептердің әмбебаптығының теориялық негіздемесі, оны ақыл-ой әрекетінің мақсаты, ұғымдарды қалыптастыру және ойлауды дамыту құралы және сараланған оқыту кезінде есептерді шешу дағдыларын қалыптастыруға бағытталған есептер жүйесін құру принциптері ретінде анықтауға мүмкіндік береді.
3. Сараланған оқыту жағдайында математикалық есептерді шешу бойынша оқушылардың оқу іс-әрекетін ұйымдастыру және есептерді шешудің жалпыланған тәсілін қалыптастыру кезінде оқытуды саралауды жүзеге асырудың әдістемелік жүйесі.
4. Дифференциалды оқыту кезінде математикалық есептерді шешуге оқыту әдістемесі.
Зерттеу әдістері мен кезеңдері: Зерттеу жұмысы екі кезеңге бөлінеді. Әр кезеңде қойылған міндеттерге сәйкес зерттеу әдістері қолданылды.
Бірінші кезеңде (2019-2020 ж.ж.) психологиялық-педагогикалық, әдістемелік әдебиеттер зерттелді, эмпирикалық материалдар жинақталды, пайдаланылған оқу-әдістемелік әдебиеттерге, нормативтік және бағдарламалық құжаттарға талдау жүргізілді, орта мектеп оқушыларын математикалық есептерді шешуге оқытудың қалыптасқан практикасы арасындағы қайшылықтар анықталды; гипотезаның жұмыс нұсқасы тұжырымдалды; зерттеудің тұжырымдамалық аппараты қалыптасты және жүйеленді. Дидактикалық материалдар, оның ішінде математикалық есептерді шешудің жалпыланған дағдысын қалыптастыру құралы ретінде қызмет ететін есептер жүйесі жасалды.
Екінші кезеңде (2020-2021 ж.ж.) теориялық және эмпирикалық материалдарды жүйелеу және сыни талдау, тұжырымдамалық деңгейде нақтылау және қорыту жүргізілді, гипотеза нақтыланды; оқушылардың математикалық есептерді шешу дағдыларының қалыптасу деңгейін анықтау мақсатында диагностикалық жұмыс жүргізілді; оқытуды саралау жағдайында есептерді шешуге оқытудың ұсынылып отырған әдістемесін тәжірибелік-эксперименттік жұмыс және сынақтан өткізу жүзеге асырылды. Оқыту эксперименті және зерттеу барысында алынған эксперименттік және теориялық материалдарды қорыту жүзеге асырылды, түпкілікті тұжырымдар мен ұсынымдар және оларды енгізу қалыптастырылды; диссертациялық жұмыс ресімделді.
Диссертация құрылымы және көлемі. Диссертация кіріспеден, екі бөлімнен, қорытындыдан, пайдаланылған әдебиеттер тізімінен және қосымшалардан тұрады.
Кіріспеде зерттеу тақырыбының көкейкестілігі негізделді, зерттеудің мақсаты, міндеттері, нысаны, әдіснамалық және теориялық негіздері мен болжамы анықталды, ғылыми жаңалығы, зерттеудің теориялық және практикалық маңыздылығы, жүргізілген жұмыстың кезеңдері мен әдістері, қорғауға ұсынылатын негізгі қағидалар, сынақтан өткізу мәліметтері мен зерттеу нәтижелері бойынша жарияланымдар тұжырымдалды.
Бірінші Мектеп математикалық есептерін шығаруды оқытудың теориялық негіздері бөлімінде есеп, есепті шығару ұғымдарының мәні, математиканы оқыту процесіндегі есептердің рөн функциясы, классификациясы айқындалды, математикалық есептерді шығару біліктігін қалыптастыруға бағытталған деңгейлік есептер жүйесін құрастыру принциптері, есептерді шығару әдістері негізделді.
Екінші Математикадан есептерді шығаруды оқытудың әдістемесі бойынша тәжірибелік жұмыс бөлімінде математикалық есептерді шығаруды оқыту бойынша оқушылардың оқу іс-әрекетін ұйымдастыру тәсілдері мен негізгі мектептің алгебра курсында мәтінді және стандартты емес есептерді шығаруды оқыту әдістемесі берілді. Эксперименттік зерттеу жұмысының нәтижелері жинақталды, талдау жасалынды және қорытындыланды.
Қорытындыда зерттеу барысында алынған ғылыми-педагогикалық нәтижелердің маңыздылығы сипатталып, негізгі теориялық және тәжірибелік қорытындылары, әдістемелік ұсынымдар тұжырымдалған, зерттеу мәселесінің одан әрі келешегі айқындалған.
Пайдаланылған әдебиеттер тізімі зерттеу барысында талданған философиялық, психологиялық, педагогикалық, әдістемелік және арнаулы әдебиеттер қамтылған.
Қосымшада зерттеу барысында қолданылған материалдар келтірілген.

1 МӘТІНДІ ЕСЕПТЕРДІ ШЕШУДЕ ОҚУ ІС-ӘРЕКЕТІНІҢ ӘДІСТЕРІН ҚАЛЫПТАСТЫРУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ

1.1 Мәтінді есеп түсінігі. Мәтінді есеп құрылымы. Мәтінді есептердің классификациясы

Мәтінді есеп анықтамасын айтпас бұрын, есеп ұғымына тоқталып өтейік. Есеп ұғымы өмірде, әртүрлі ғылымдарда әрі сабақ пәндерінде кеңінен қолданылады: психология, логика, педагогика, математика, физика т.б. Бұл термин көптеген ұғымдарды білдіреді. Сондықтан есеп ұғымына жалпы анықтама беру аса қиын, бұл ұғымның нақтылы түсіндірмесі жоқ. Есеп ұғымы психологиялық-педагогикалық, жаратылыстану-метематикалық әрі әдістемелік ғылымдардағы күре ұғымдардың бірі боп табылады. Осы тұжырымдаманы енгізу бойынша әдістемелік қамсыздандырудың дамуына Н.Г. Алексеев, Г. А. Балл, Л. Л. Гурова, В. В. Давыдов, Ю. М. Колягин, В. И. Крупич, г. л. Луканкин, Л. М. Фридман, А. А. Столяр, П. М. Эрдниев және т. б. елеулі үлес қосты.
Есеп сөзіне сипаттама беру үшін сандаған жұмыстар арналған. Математиканы оқыту әдістемесінде көптеген жылдар бойы есептің ендігі жіктеулер кең таралған:
а) дәлелдеуге арналған есептер;
б) құрылысқа арналған есептер;
в) есептеуге арналған есептер.
Бұл жіктеулер айтулы есептердің түр түрін шешу әдісін алдын ала анықтаған. Дегенмен, оқу мақсаттарының кеңеюіне қатысты мектеп математика курсында дәстүрлі типологияға лайық келмейтін есептер те кіріс бола бастады. К. И. Нешков және А. Д. Семушин басқа жіктеулерді де ұсынған. Олар ендігі түрде:
а) дидактикалық функциялары бар есептер;
б) танымдық функциялары бар есептер;
в) өсу функциялары бар есептер.
Г. И. Саранцевтің пікірінше, есептер мен жаттығуларды оларды шешу жолдары бойынша топтастыру қажет: геометриялық түрлендірулерге есептер, векторларға есептер және т.б. шарттағы объектілер санына әрі олардың арасындағы байланыстарға қатысты есептер, күрделі және қарапайым есептер боп бөлу тиіс. Сонымен қоса, стандартты және стандартты емес, теориялық және практикалық есептер боп үлестіру қажет.
Адам өмірде де, әртүрлі пәндерді үйрену кезінде де үнемі есептерге тап болады. Ғылымның әртүрлі салаларында (психология, педагогика, математика) есеп ұғымын Г.А. Балл, Ю. М. Колягин, Л. М. Фридман, В. И. Крупич, А. Ф. Эсаулов, П. М. Эрдниев және басқалар зерттеді.
Мектептегі математика курсында шешілетін есептер өте алуан түрлі. Белгілі бір есепті шешудің әдісін, тәсілін анықтау үшін осы есептің түрін анықтау қажет.
Л.Д.Жумалиева өзінің Орта мектепте математикалық есептерді шығаруды оқытудың әдістемелік негіздері тақырыбындағы диссертациясында математикалық есептерді келесідей классификациялаған (1-сурет):

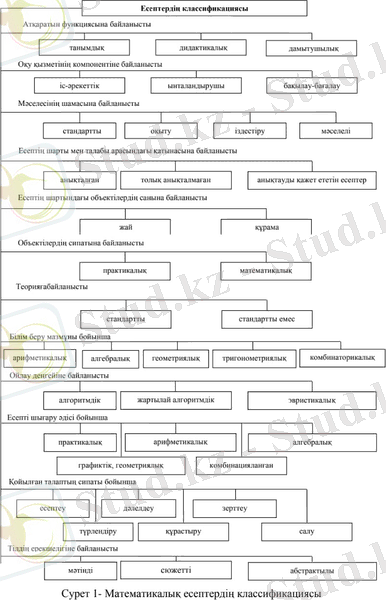
1-сурет
Осы жіктемеге сәйкес есептің тілдің ерекшелігіне байланысты мәтінді болып бөлінетінін аңғаруға болатынын көруге болады. Алайда, бүгінгі таңда мәтінді есеп терминін анықтауға бірыңғай көзқарас жоқ. Мысалы, Г.А. Балл өзінің есеп ұғымының психологиялық мазмұны туралы мақаласында мәтінді есеп ұғымын нақты анықтауға болмайтыны айтады. Бұл термин психологиялық және педагогикалық әдебиеттерде үш түрлі санатқа жататын объектілерді белгілеу үшін қолданылады дейді:
1) субъектінің іс-әрекет мақсаты (іс-әрекет мақсаты, міндетті талап ету) санатына;
2) оған қол жеткізілуі тиіс жағдайларды қоса алғанда, жағдай (проблемалық жағдай) санатына;
3) осы жағдайды сөзбен тұжырымдау санатына жатқызады.
Г.А. Балл психологиялық әдебиеттерде екінші санатқа сілтеме жасау үшін есеп терминін қолдану жиі кездеседі деп санайды. Әр түрлі анықтамаларды талдай отырып, Г. А. Балл осы сөздің екінші санаттағы есеп анықтамаларының келесі тізбегін береді:
1. Есеп - бұл субъектіден белгілі бір әрекетті талап ететін жағдай.
2. Есептің міндеті - белгілі бір адаммен байланысын пайдалану негізінде белгісізді табуға бағытталған белгілі бір әрекетті талап ететін жағдай.
3. Мәтінді есеп - субъектіден белгілі бір әрекетті талап ететін жағдай, ол субъект осы әрекет (алгоритмі) болмаған жағдайда оның белгілі бір байланысын пайдалану негізінде белгісізді табуға бағытталған.
Л. Ф. Фридман Г.А. Баллдың осы мәселе бойынша пікірін қолдай отырып, мәтінді есеп проблемалық жағдай негізінде туындайды, сонымен қатар осы проблемалық жағдайдың үлгісі ретінде кейбір тіл белгілерін қолдана отырады дейді. Л. М. Фридман мәтіндік есептің формальды анықтамасын ұсынады. Оның көзқарасы бойынша әр есеп келесі 4 бөлімнен тұрады:
1. пәндік аймақ - бұл есепте қарастырылатын объектілер жиынтығы;
2. пәндік аймақтың объектілерін байланыстыратын қатынастар;
3. талаптар - бұл есепті шешудің мақсатын көрсету (шешім нәтижесінде не анықталуы керек);
4. оператор - оның талабын орындау үшін есептің шарттары бойынша орындалуы керек әрекеттер жиынтығы.
Есептің шарты - пәндік аймақтың элементтері мен олардың арасындағы қатынасты көрсететін оның тұжырымдамасының бөлігі.
Пәндік аймақтың элементтері мен олардың арасындағы қатынасты белгілі (есепте олардың мәндері нақты көрсетілген) және белгісіз (ізделінді (мәндері табылуы керек) және көмекші) деп бөлуге болады.
Бұл тұжырымдамаларға А.В. Брушлинский және А. М. Матюшкин келіспейді. Мысалы, А. М. Матюшкин өзінің келіспеушілігін мәтінді есеп және есеп ұғымдарын ажырату қажеттілігімен негіздейді. Ол мәтінді есеп ұғымы мен есеп ұғымы әртүрлі психологиялық шындықтарды білдіретін түбегейлі әр түрлі ұғымдар екендігі анық деп жазады. А. В. Брушлинский айтылғанға қосымша, мәтінді есептің айырмашылығы:
а) берілгенді және белгісізді алдын-ала айырып алу мүмкін болды;
б) есептің бастапқы шарттары (берілген, белгілі және т.б.) және талап (дәлелдеу, табу, анықтау, есептеу және т. б. қажет) нақты белгіленген.
Мәтінді есептің бұл сипаттамасында оның құрылымы өте айқын көрсетілген: берілген (белгілі), белгісіз (ізделетін), шарт - талап.
С. Е. Царева өз жұмысында мәтіндік есеп және оқу есебі ұғымдарының арасындағы айырмашылықтарды атап өтіп, оқушылардың есептермен жұмыс жасау мақсатын түсініп, қабылдаған кезде мәтіндік есеп оқу тапсырмасының элементіне айналатынын баса айтады. Яғни, мәтіндік есеп білім алушылар қарастыратын оқу мақсатымен бірге оқу есебін құрайды.
Алғаш рет есептерді жалпы түрде шешу әдістемесін Дьерд Пойа әзірледі және әйгілі "Есепті қалай шешуге болады" (How to Solve It) кітабында сол әдістемені ұсынды.
Көптеген ғалымдар мәтінді есептерді түсінуді зерттеген. Кейбір ғалымдар мәтінді есептерді шешуге әсер ететін қиындықтарды зерттеді. Ең үлкен кедергі - оқу, есептеу және математика дағдыларының болмауы. Егер оқушылар мәтінде не айтылғанын түсіне алмаса, олар есепті шешу үшін ойлау процесін бастай алмайды. Оқушылар тек шектеулі кілт сөздерді немесе техникалық терминдерді біледі. Олар ұзындығы мен күрделілігіне байланысты мәтінді есептерге қызығушылық танытпайды. Кейбір зерттеушілер оқуды түсіну мен математикадағы жетістіктер арасындағы байланысты зерттеді.
Мәтіндік есеп анықтамасын кейбір математика мұғалімдері келесідей анықтауға тырысты. Кейбір ғалымдар мәтінді есеп сандық жауап түрінде жауап беруді қажет ететін жағдай немесе сұрақ деп санайды. Бұл есепті шешу үшін білім мен тәжірибені қолдана отырып, осы жағдайдың дұрыс әдісін табу керек. Кейбір ғалымдар мәтінді есепті сөз есеп, тарихи есеп немесе ауызша есеп ретінде анықтауға болады деп болжайды. Бұл есепті сандық жауапты қажет ететін сөздермен немесе сандармен сипаттау.
Кейбір ғалымдар мәтінді есеп математикаға қатысты сұрақ немесе жағдай деп санайды, бірақ тек сандармен байланысты емес. Кейбір мәтінді есептер физикалық қасиеттермен немесе сандармен байланысты емес логикалық ойлаумен байланысты болуы мүмкін. Осылайша, мәтінді есептер математикаға байланысты сұрақ немесе әр түрлі болатын жағдайды білдіреді. Бұл нағыз өмірде кездесетін нақты жағдай, оны шешу үшін дұрыс әдіс пен математикалық білім қажет.
Мәтіндік есеп - бұл арифметикалық амалдардың көмегімен жауап алуға болатын сөзбен тұжырымдалған сұрақ дейді М. И. Моро және А. М. Пышкало.
Олардың зерттеуінше кез-келген мәтінді есептің құрылымы:
1. Белгілі бір қасиеттері бар деректер;
2. Сол деректер арасындағы қатынастар;
3. Қажетті деректер және олардың қасиеттері;
4. Деректер мен ізделгендер арасындағы байланыс.
5. Қажетті нәрсені табу қажеттілігін көрсету.
Белгілі бір қасиеттері бар деректер, олардың арасындағы қатынас, сондай-ақ деректер мен ізделгендер арасындағы қатынастар мәтінді есептің шарты деп аталады. Қажетті және оны табу қажеттілігін көрсету мәтінді есептің талабы деп аталады.
Мәтінді есептерге басқа да көптеген ғалымдар анықтама берген:
1. Математиканың бастапқы курсындағы мәтінді есеп сандық компоненттермен сипатталған белгілі бір күнделікті жағдайды сипаттайтын арнайы мәтінді білдіреді (А. В. Белошистая)
2. Мәтінді арифметикалық есептер дегеніміз - күнделікті мазмұны бар және арифметикалық амалдардың көмегімен шешілетін есептер (А.А. Столяр, В. А. Дрозд).
3. Мәтінді есеп - бұл кейбір шамалардың мәндері енгізілген әрі мәліметтерге тәуелді әрі шартта көрсетілген белгілі бір қатынастармен байланысты басқа шамаларды табу керек есеп (А. А. Свечников).
4. Мәтінді есеп белгілі бір сандық сипаттамаларды немесе мәндерді табу үшін белгілі бір өмірлік сюжетті (құбылыс, оқиға, процесс) сипаттайтын есептерді білдіреді (Л.П. Фридман).
5. Мәтінді есеп - бұл жағдайдың кез-келген компонентіне сандық сипаттама беру, оның компоненттері арасында қандай-да бір қатынастардың болуын немесе болмауын анықтау немесе осы қатынас түрін анықтау талап етілетін табиғи тілдегі кейбір жағдайларды сипаттау (Л.П. Стойлова, А. М. Пышкало, В. В. Статкевич).
6. Мәтінді есеп сандармен байланысты және оларға арифметикалық амалдарды орындауды талап ететін өмірлік жағдайды білдіреді. (М. А. Бантова)
7. Мәтінді есеп - бұл жағдайдың белгілі бір компонентіне сандық сипаттама беруді (белгілі бір шаманың сандық мәнін басқа шамалардың белгілі сандық мәндерімен және олардың арасындағы тәуелділіктермен анықтау) немесе оның құрамдас бөліктері арасында қандай да бір қатынастардың болуын немесе болмауын анықтау немесе осы қатынас түрін анықтау немесе қажетті әрекеттер тізбегін табу (яғни Демидова, А.П. Тонких).
8. Есеп - бұл қасиеттері мен қатынастарымен және іздегендерін табу қажеттілігін көрсететін мәліметтер жүйесі (Г. Т. Зайцев)
9. Кез-келген есеп - бұл белгілі бір жағдайларда берілген шындық құбылыстары (объектілер мен процестер) және олардың сипаттамалары туралы кез-келген білімді табу немесе қажетті практикалық нәтиже алу (бірдеңе құру, қандай да бір шарттардың орындалуын қамтамасыз ету және т.б.) (И. И. Илиясов).
10. Мәтінді есеп - табу (орнату, анықтау) белгілі бір объектінің басқа сипаттамаларына сәйкес кейбір сипаттамалары (Л.П. Фридман).
11. Есеп - бұл арифметикалық амалдардың көмегімен жауап алуға болатын сөзбен тұжырымдалған сұрақ (И.Н. Моро).
12. Есеп - бұл байланыс алдын-ала анықталған элементтердің бос емес жиынтығы (О.Б. Епишева, В. И. Крупич).
Осылайша, қазіргі әдістемелік әдебиеттерде мәтінді есеп былайша түсініледі:
1. Белгілі бір күнделікті жағдай сипатталған мәтін (А. В. Белошистая, А. А. Свечников, А. А. Столяр, В. А. Дрозд)
2. Белгілі бір өмірлік сюжетті сипаттайтын математикалық есеп (Л.П. Фридман).
3. Өмір сүру жағдайы (яғни Демидова, п.п. жіңішке, Л. П. Стойлова, А. М. Пышкало, М. А. Бантова).
4. Деректер және іздеушілер жүйесі (Г. Т. Зайцев [24])
5. Талап (И. И.Ильясов, И. Н. Моро, Л. П. Фридман).
6. Көптеген элементтер (О.Б. Епишева, В. И. Крупич, Ю. М. Колягин). Осы анықтамалардың барлық түрлерін түсіну үшін осы тұжырымдаманың негізгі белгілерін анықтау қажет. Атап айтқанда, Я. А. Пономарев өз зерттеулерінде әртүрлі анықтамалардың жалпы, маңызды және бұл жалпы табу қажеттілігін көрсетеді және есеп ұғымын анықтауға негіз болатынын айтты . Мәтінді есеп ұғымының негізгі белгілерін зерттеу оның құрылымының компоненттерін анықтауды қамтиды.
Есеп ұғымының барлық қарастырылған анықтамаларында көптеген ұқсастықтар бар, сонымен бірге кейбір айырмашылықтар да бар. Ұқсастығы - бұл берілген немесе белгілі, ізделетін немесе белгісіз объектілерден, объектілердің қасиеттерінен немесе олардың арасындағы қатынастардан, ізделгенді табу шарттарынан немесе талабынан тұратын есептің құрылымы. Айырмашылық, негізінен, кейбір анықтамаларда есептің жалпы құрылымы жалпы ұғым ретінде қабылданады: шарт пен талап арасындағы қатынас (А. А.Матюшкин), проблемалық жағдайдың моделі (Л. М. Фридман), басқаларында оның түпкі мақсаты: мақсат (А. Н. Леонтьев), қажетті нәрсені табу талабы (С. О. Шатуновский). Бірақ бұл айырмашылық, жоғарыда атап өткеніміздей, тапсырманың құрылымына әсер етпейді. Сондықтан есеп ұғымын анықтауда құрылымды бастапқы позиция деп санаған жөн. Алайда, бүгінгі таңда есеп құрылымының компоненттеріне қатысты бірыңғай тәсіл жоқ. Мысалы, А. А. Свечников [8] және В.В. Статкевич [9] мәтінді есеп құрылымында келесі құрама элементтерді ажыратады:
а) шарт:
- мәтіннің ауызша мәлімдемесі, онда шамалар арасындағы функционалды байланыс ашық немесе жабық түрде көрсетілген;
- есеп мәтінінде айтылған шамалардың сандық мәндері немесе сандық мәліметтер;
б) бір немесе бірнеше шамалардың белгісіз мәндерін білу ұсынылатын сұрақ.
Мәтінді есеп құрылымының компоненттер жүйесін негіздеу үшін Ю. М. Колягиннің және В. И. Крупич зерттеулеріне жүгінеміз, онда авторлар мәтінді есеп құрылымының компоненттерін мұқият зерттеді. Есепті жүйе ретінде қарастыра отырып, Ю.М. Колягин ондағы ACRB компоненттерін анықтайды, мұндағы А - бастапқы күй (мәселенің шарты); С - есепті шешудің негізі (есепті шешудің теориялық негіздемесі); R - есепті шешу (қажетті нәрсені табу үшін есептің шартын өзгерту әдісі); В - соңғы күй (есептің талабы немесе шарты).
В. И. Крупич мәтінді есепте екі ақпараттық компонент бар: субъективті және объективті, сыртқы (ақпараттық) және ішкі құрылымдар деп бөледі. Ю. М. Колягин, В. И. Крупич тәсілін ескере отырып, ақпараттық құрылымды ACRDB элементтерінен тұратын жүйе ретінде қарастырады, мұндағы А - есептің шарты (мәліметтер және олардың арасындағы қатынастар); С-есепті шешудің негізі ( есепті шешуді негіздеу үшін қажет теориялық және практикалық негіз); R-деректер мен ізделгендер арасындағы қатынастар жүйесіндегі негізгі қатынас; D-есепті шешу процесін анықтайтын әдіс.; В-есептің талабы немесе мақсаты (ізделетін (ізделетін) және олардың арасындағы қатынастар). Ю. М. Колягиннен айырмашылығы, В. И. Крупич ақпараттық құрылымның құрамына R компонентін енгізеді (мәліметтер мен ізделгендер арасындағы қатынастар жүйесіндегі негізгі қатынас), оны анықтау, автордың пікірінше, есептің ішкі құрылымын, оның элементтерін және олардың арасындағы байланыстарды құру үшін негіз болып табылады.
Есептің ішкі құрылымы бойынша В. И. Крупич қарастырылып отырған жүйенің элементтерінің, байланыстардың және байланыс түрлерінің жиынтығын білдіреді. Сыртқы және ішкі құрылым арасындағы байланыс D және C компоненттерінің көмегімен орнатылады.
Мәтінді есептің әр компонентін қарастырайық. Шарт пен талаптан бастайық. Мәтінді есептің анықтамасына байланысты авторлар осы ұғымдардың әртүрлі анықтамаларын береді. Міне, олардың кейбіреулері. Шарт:
- бұл берілген нәрсе (А. К. Артемов, Т. В. Семенов);
- бұл белгілі бір қатынастармен реттелген объектілердің қолма - қол жиынтығы (Ю. Н. Кулюткин);
- бұл шамалар арасындағы байланыс (мәліметтер мен ізделгендер арасындағы байланыс сипатын көрсететін ауызша материал) (В. В. Станкевич);
- бұл есеп объектілерінің сандық және сапалық сипаттамалары және олардың арасындағы қатынастар, сондай-ақ деректер мен іздеушілер арасындағы қатынастар (яғни Демидова, а.п. Тонких, Л. П. Стойлова, г. Т. Зайцев).
А. К. Артемовтың және Т. В. Семеновтың шарттарын анықтауда есептің мәтінінен шарттың құрамдас бөлігі ретінде не ажырату керектігі туралы түсінік жоқ, сондықтан оны іс жүзінде қолдану қиын деп тұжырымдайды.
Ю. Н. Кулюткин мен В. В. Станкевичтің анықтамаларында есеп объектілері арасындағы қатынастарға баса назар аударылады, бірақ объектілердің сапалық немесе сандық сипаттамалары назардан тыс қалады. Айта кету керек, мәтінді есепте әдетте бір емес, бірнеше шарттар бола алады.
Талап:
- бұл осы жағдайларда не іздеу керек екенін көрсету (Ю. Н. Кулюткин);
- бұл не нәрсеге ұмтылу керек немесе қол жеткізу керек (А.К. Артемов, Т. В. Семенов);
- бұл онда не табу керектігін көрсететін мәселе (В. В. Станкевич);
- бұл оны табу қажеттілігін іздеу және көрсету (Г. Т. Зайцев).
Барлық дерлік авторлар өз анықтамаларында іздегендердің болуын және оны табу талаптарын көрсетеді.
Талаптар сұрақ түрінде де, баяндау түрінде де тұжырымдалуы мүмкін екенін есте ұстаған жөн. Бір есепте бірнеше болуы мүмкін. Ю. М. Колягин, Л.Ф. Фридман, О. Б. Епишева, В. И. Крупич есептің құрамдас бөліктеріне пәндік аймақ, яғни тапсырмада талқыланатын элементтердің бос емес жиынтығы жатады деп айтады. Л. Фридман элементтердің сипаттамасы олар сипаттайтын жеке шамалардың мәтінді есептерінің мәтініндегі толық және толық емес тапсырмаларды қамтитынын айтады.
Толық сөздік тапсырма:
1) мәні болып табылатын шаманың атауын;
2) осы мәннің оны сол шаманың басқа мәндерінен ажырататын ерекшеліктерін көрсетуді;
3) егер бұл мән белгілі болса, осы мәннің атаулы сан түріндегі мөлшерін қамтиды.
Толық емес ауызша тапсырма мыналармен сипатталады:
1) бірінші бөлімді елемеуге болады және тек қана осы бөлімді;
2) екінші бөлік минимумға дейін қысқартылуы және тіпті толық түсірілуі мүмкін, бірақ оның орнына қандай да бір жанама нұсқаулар беріледі, мысалы, санның атауы түрінде-мәннің мөлшері және т.б.;
3) ауызша тапсырмада үшінші бөлік шамасының мәні болмаған жағдайда - оның аталған сан түріндегі мөлшері.
Мәтін есептің толықтығы деңгейі бойынша шамалар:
1) анық берілген шамалар - осы сипаттаманың мәні (сандық немесе қандай да бір өзге) көрсетілген кезде объектілердің сипаттамалары нақты болуға тиіс;
2) нақты емес - объектілердің сипаттамалары тек аталған, бірақ олардың тапсырмадағы мәні берілмеген болуы мүмкін;
3) анық берілмегендер - есептің мәтінінде көрсетілмеген және есепте сипатталған құбылысты терең талдау кезінде ғана анықталатын объектілердің сипаттамалары.
Бірінші жағдайда пәндік аймақтың тиісті объектілері белгілі, ал екінші және үшінші жағдайда белгісіз болып саналады.
Белгісіздер, өз кезегінде, ізделетін (табу немесе орнату қажет), аралық немесе көмекші (табу қажет емес, бірақ оларды іздеу процесінде табу керек) және белгісіз (қажет емес және табу мүмкін емес) болып бөлінеді. Есеп оның элементтерін сипаттайтын шамалардың мәндерін өзгертуді қамтиды. Әрбір осындай өзгеріс қарастырылатын жиынның немесе оның ішкі жиынының белгілі бір күйін анықтайды. Бұл қатынастар мен байланыстар белгілі және белгісіз болуы мүмкін, оның ішінде ізделгендер де бар.
Мәтінді есеп, әдетте, бірнеше қатынастарды қамтиды ( берілген мәліметтер арасында, берілген мәліметтер мен іздеулер арасында, іздеулер арасында). Бұл жағдайда Л. М. Фридман қатынастардың екі тобын ажыратады:
Бірінші топқа бірдей шаманың мәндері арасындағы қатынастар жатады. Онда екі түрді ажыратуға болады:
1 түрі - бөліктер мен бүтіннің қатынасы. Ол: шаманың бірнеше мәнін сол шаманың бір мәніне қосу операциясымен; оның бір бөлігінің бүтінінен алу операциясымен сипатталады.
2 түр - бірдей шаманың мәндерін салыстыру қатынасы: бірдей шаманың мәндері арасындағы теңдік қатынасы; бірдей шаманың екі мәні арасындағы теңсіздік қатынасы; бірдей шаманың екі мәнін айырмашылықпен салыстыру қатынасы (бір мән басқасынан қаншалықты үлкен немесе аз); бір шаманың екі мәнін бірнеше рет салыстыру қатынасы (бір мән басқасынан қанша есе көп немесе аз)); бүтін бөліктің пайыздық қатынасы немесе қатынасы (бір бөліктің қандай бөлігі немесе қандай пайызы екіншісінен тұрады).
Қатынастардың екінші тобы әртүрлі шамалардың мәндері арасындағы қатынастардан тұрады, оның ішінде: бір санау немесе өлшеу бірлігінен екіншісіне ауысу; бүтіннің тең бөліктерге бөлінуі; әртүрлі шамалардың мәндері арасындағы байланыс. Мәтінді есептің шарты мен талабына кіретін және оның пәндік аймағында жүзеге асырылатын шамалар арасындағы функционалдық қатынасты білдіретін қатынас негізгі деп аталады. Мәтінді есепте жүзеге асырылған негізгі қатынас арқылы ресімделген сөйлем жағдай деп аталады. Сонымен қатар, әр есепте бір немесе бірнеше жағдай болады.
Мәтінді есепті шешу барысында мұндай немқұрайлылыққа жол бермеу керек, өйткені бір қарағанда, маңызды емес факт мәселені шешудің кілті болуы мүмкін. Есептің логикалық дұрыстығына байланысты Л.М. Фридман дұрыс есептерге қойылатын мынадай талаптарды тұжырымдайды:
1) Есепте көрсетілген пәндік аймақтың барлық элементтері болуы тиіс;
2) Есепте көрсетілген барлық қатынастар есеп шартында берілген пәндік аймақтың элементтері үшін шын мәнінде анықталуы тиіс;
3) Есепте берілген айнымалылардың әрқайсысының мәндер саласы бос болмауы тиіс;
4) Есеп шартында берілген барлық мәлімдемелер шын болуы тиіс;
5) Есеп шартында берілген мәлімдемелер бір-біріне қайшы келмеуге тиіс;
6) Егер есептің мақсаты белгілі бір мәлімдемелік нысанды шынайы мәлімдемеге айналдырудан тұрса, онда есеп шартында ол үшін ең болмағанда кейбір негіздер көрсетілуге тиіс. Логикалық тұрғыдан дұрыс емес есептер - бұл тұжырымдарға қарсы есептер. Кейбір ұқсас есептерді шешуге мүмкіндік бар екеніне қарамастан, оны қабылдау мүмкін емес. Мұндай шешім мағынасы жоқ болғандықтан, мұндай есептерде жауап тек есеп дұрыс қойылмаған немесе есепті шешу мүмкін емес болуы мүмкін.
Жоғарыда көрсетілген талдау бізге мәтінді есеп құрылымының келесі компоненттерін бөліп көрсетуге мүмкіндік берді:
1) тапсырманың элементтері:
а) белгілі (анық көрсетілген);
б) белгісіз (нақты емес, анық емес): ізделгендер (оларды табу немесе орнату қажет); аралық немесе көмекші (табу қажет емес ,бірақ олар ізделгендерді іздеу процесінде табылуы керек);
2) Элементтер сипатталған шамалар (есептің мәтінінде қанша және қандай шамалар анық немесе анық берілген; шаманың әрбір мәнінің сипаты);
3) Элементтер арасындағы өзара байланыстардың сипаты;
4) шамалар арасындағы негізгі қатынас;
5) оның элементтерін сипаттайтын шамалар мәндерінің өзгеруі;
6) есепте іске асырылған негізгі қатынастармен ресімделген сөйлем.
Жоғарыда аталған компоненттерді ескере отырып, мәтінді есеп - бұл элементтің кез-келген сипаттамасын табу немесе элементтер арасындағы қатынасты орнату немесе қажетті әрекеттер тізбегін табу талабымен берілген қатынасты анықтайтын элементтердің кейбір бос емес жиынтығының әңгіме түріндегі сипаттама деп айтуға болады.
Мәтінді есеп - бұл жағдайдың кез-келген компонентіне сандық сипаттама беру, оның құрамдас бөліктері арасында қандай-да бір қарым-қатынастың болуын немесе болмауын анықтау немесе осы қарым-қатынастың түрін анықтау талап етілетін табиғи тілдегі жағдайдың сипаттамасы(А.П. Тонких).
Сонымен, мәтінді есеп - бұл қасиеттері мен қатынастарымен және іздегендерін табу қажеттілігін көрсететін мәліметтер жүйесі.
Т. А. Иванованың оқулығында және О. П. Шарованың мақаласында мәтінді есептер математиканың маңызды бөлімі болып табылады. Шарт пен талап арасындағы байланыс сөзбен тұжырымдалған есеп мәтінді деп аталады. Егер есеп нақты объектілер, процестер, байланыстар мен қатынастар туралы болса, онда есеп мәтінді деп айтады.
Мәтінді есептердің кез-келген типологиясы шартты және көптеген жағдайларға байланысты. Мәселен, бірдей есепті көптеген жолдармен шешуге болады. Есепті проблемалық дәреженің белгілі бір түріне жатқызу көбінесе бұл есепті кім шешетініне байланысты. Осыған қарамастан, әртүрлі типологиялар мұғалімге оқу мақсаттарына байланысты есептерді таңдауға саналы түрде жүгінуге мүмкіндік береді.
Мәтінді есеп белгілі бір жағдайды (құбылысты, процесті) табиғи және (немесе) математикалық тілде сипаттауды, осы жағдайдың қандай да бір компонентіне сандық сипаттама беруді немесе оның құрамдас бөліктері арасында қандай да бір қатынастардың болуын немесе болмауын анықтау немесе осы қатынас түрін анықтау немесе қажетті әрекеттер тізбегін табу.
Мәтінді есеп жағдайдың, құбылыстың, оқиғаның, процестің және т.б. ауызша моделі деп айтуға болады.
Сонымен ғалымдардың ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.