Негізгі мектеп алгебра курсында функцияны оқыту: теориялық негіздері мен әдістемелік нұсқаулар


КІРІСПЕ
Тақырыбының өзектілігі. Функция ұғымы фундаменталды математикалық ұғымдардың бірі болып табылады. Функция нақты өмірмен тікелей байланысты. Онда нақты әлемнің өзгергіштігі мен динамикасы, нақты әлемнің өзара шарттылығы айқын бейнеленген. Функциялар, олардың қасиеттері мен графиктері мектеп математика курсының негізін құрайды. Күннен күнге оқушылардың алған білім, білік және дағдылардың сапасына қойылатын талаптар артып отыр. Осыған байланысты математиканы оқытудың теориясы мен әдістемесінде көптеген әдістемелік мәселелер туындайды. Соның ішінде негізгі мектепте функцияларды оқыту мәселесі өзектілігін жойған жоқ. Мектептегі математика курсында функцияларды оқыту мәселесі ғылыми әдебиеттерде кеңінен талқыланған.
Математиканы оқытудың әдістемесі, болашақ математика мұғалімдерін дайындау мәселелерімен біздің елде белгілі математиктер мен әдіскерлер
А. Е. Абылкасымова, С. М. Кеңесбаев, Е. Ө. Медеуов, А. Н. Нұғысова, Қ. Қ. Рахымбек, Б. Р. Қасқатаева, Ж. Нурмухамбетова және т. б. ғалымдардың ғылыми-зерттеу жұмыстарында әр қырынан зерттелген.
Мектептегі математика курсында функцияларды оқыту мәселесі ғылыми әдебиеттерде кеңінен талқыланған. Әдіскер ғалымдар аталған мәселені шешудің әртүрлі жолдарын қарастырды. Мәселен, математиканы оқыту процесінде жаттығуларды қолдану әдістемесі жасалды, функция ұғымын қалыптастыру процесінде жаттығуларды таңдау және жобалау критерийлері ұсынылды (Г. И. Саранцев) [137-139] ; графикалық бақылаумен есептеу жаттығуларының жүйесі құрылды (В. А. Гусков) [46] ; оқушылардың графикалық көріністерін қалыптастыру және жетілдіру әдістемесі жасалды (Е. С. Канин) [61] ; орта мектепте оқушылардың бастапқы функционалдық дағдыларын қалыптастырудың негізгі кезеңдері анықталды, математиканы оқытуда пәнішілік және пәнаралық байланыстарды нығайтуға ықпал ететін функционалдық дағдылардың қалыптасу деңгейін арттыру әдістемесі жасалды (М. В. Ткачева) [155] ; өзара кері функциялар негізінде функция ұғымын зерттеу әдістемесі ұсынылды (В. П. Черепков) [174] ; функционалдық тәуелділіктің пропедевтикасының кейбір мәселелері әзірленді (А. И. Жаворонков [54] ) .
Осыған қарамастан, тиісті басылымдарда оқушылардың функционалдық білімі, дағдылары мен дағдыларының қалыптасу деңгейінің төмендігі көрініс тауып отыр. Оқушылар функция ұғымын формуламен байланыстыра отырып, үстірт игереді. Бұған ықпал ететін себептердің ішінде көптеген фактілер келтірілген: оқушылардың жалпы пәнге қызығушылығының болмауы және функцияларды зерттеу; функцияның әрбір жаңа түрін, функцияның қасиеттерін іс жүзінде алдыңғысымен байланыстан тыс зерттеу; оқушылардың есептеу және функционалдық-графикалық дағдылары арасындағы алшақтық.
Сонымен қатар, физика, география, информатика және биология мәселелерін шешуде білім алушыларға әртүрлі функционалды желілермен жұмыс істеу мүмкіндігі қажет. Бұл баланың алдында функция ұғымын ашу, оны практикалық есептерді шешуде алған білімдерін қолдануға үйрету математика мұғалімі үшін маңызды.
Функция күнделікті өмірде және басқа пәндерден алынған әртүрлі тәуелділіктер туралы идеяларды реттеуге мүмкіндік береді. Оқушылардың функционалдық тәуелділік тұрғысынан ойлау қабілетін дамытуға, өзара тәуелді шамалар туралы идеяны дамытуға мүмкіндік береді - бұл баланың нақты әлемді тануында үлкен рөл атқарады.
Кез-келген нақты процестің бастапқы математикалық формасы - функция болып табылады.
Мақсаты - негізгі мектептің алгебра курсында функцияны оқыту әдістемесін әзірлеу.
Міндеттері:
- Негізгі мектептің алгебра курсында функцияларды оқытудың теориялық негіздерін айқындау;
- Мектеп математика курсында функцияны оқыту әдістемелік ерекшеліктерін анықтау;
- Негізгі мектеп алгебра курсында функцияларды оқытуға арналған әдістемелік нұсқаулар дайындау.
Объект - негізгі мектепте функцияны оқыту процесі.
Пәні - алгебра курсында функцияны оқыту әдістемесі
Күтілетін нәтижелері:
1. Функционалдық білімнің негізін құрайтын элементар функциялардың графиктерін оқуға және бейнелеуге қажетті дағдылар қалыптастыратын есептер құрылды.
2. Негізгі мектеп алгебра курсында функцияларды оқытуға арналған әдістемелік нұсқаулар жасалды.
Жаңалығы.
Оқушылардың оқу-танымдық іс-әрекетке қабілеттілігін дамытуға бағытталған негізгі мектеп алгебра курсында функцияны оқыту әдістемеcі әзірленді.
Дамыту перспективалары. Тақырыпты сапалы меңгеру үшін жаттығулар кешенін дайындау.
Құрылымы: жұмыс кіріспеден, екі тараудан, қорытындыдан, пайдаланылған әдебиеттер тізімінен және қосымшалардан тұрады.
Кіріспеде жұмыстың ғылыми-әдіснамалық аппараты тұжырымдалған, яғни жоба тақырыбының өзектілігі, жобаның мақсаты мен міндеттері айқындалған, жобаның нысаны мен пәні келтірілген.
Пайдаланылған әдебиеттер тізімінде жобаны зерттеу барысында талданған, қарастырылған әдебиеттер тізімі көрсетілген.
1 НЕГІЗГІ МЕКТЕПТЕ ФУНКЦИЯНЫ ОҚЫТУДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ
- Негізгі мектептің алгебра курсында функцияны оқытудың мақсаттары, міндеттері
Функция жалпы математикалық және негізгі ғылыми үғымдардың бірі болып саналады. Ол қоршаған ортаны тануда үлкен рөл атқарды жәнә әлі де атқаруда. Математиканың (алгебра және геометрияның) негізгі түсініктері функционалды негізде қарастырылады.
Қасиеттерін қолдану математикалық есептерді шығару әдісі негізінде. Мысалы, теңдеулер мен теңсіздіктерді, олардың жүйелерін шығарған кезде көбіне сол және оң бөліктерінде тұрған функциялар мәндерінің аймақтарын салыстыру пайдалы. Олардың қиылысуы бос немесе бір нүктеге тең болуы мүмкін. Бұл теңдеуді немесе теңсіздікті шешу туралы қорытынды жасауға мүмкіндік береді. Параметрлері бар есептерді шешу кезінде тапсырмада қарастырылған функциялардың графигінің шешімін табу жиі көмектеседі. Жалпы, функционалдық графиктерді қолдануға негізделген графикалық шешім математикалық есептерді шешудің әдістерінің бірі болып табылады.
Оны оқыту оқушыларды бәріне ортақ байланыс идеясымен, үздіксіздік, шексіздік, интерполяция, яғни жуықтау идеясымен таныстырды. Уақытқа тәуелді барлық процестер функционалдық тәуелділіктер болып табылады. Функция көптеген нақты процестердің үлгісі болып табылады. Функциялардың қасиеттерін оқыту қоршаған әлем құбылыстарын оқытуғе мүмкіндік береді.
Функционалдық тәуелділіктер әртүрлі ғылымдар мен оқу пәндерінде қолданылады. Мектептегі функцияны оқыту оқушыларға осы ұғымның маңыздылығы мен кеңінен қолданылатындығын көрсетуге мүмкіндік береді. Функциялардың іс жүзінде барлық оқу пәндерінде қарастырылады. Себебі, көптеген заңдар, байланыстардың функционалдық негізі бар.
Егер біз дамыту мақсаттарын қарастыратын болсақ, онда функцияларды оқыту, ең алдымен, әртүрлі объектілердің өзгерістері арасындағы тәуелділіктерді көруге жауап беретін функционалды ойлауды дамытуға, сондай-ақ алгебралық материалды оқыту кезінде қойылған мақсаттарға жетуге ықпал етеді (абстрактілі материалмен жұмыс істеу қабілетін дамыту, талдау қабілеті және т. б. ) .
Мектеп курсында оны оқытудың міндеттері функциялар туралы маңызды түсінік беру және алгебраны академиялық оқуда да, күнделікті тұрмыста да пайдалы болатын дағды мен дағдыларды дамыту болып табылады.
Функцияны мектеп курсына енгізудің ең бастапқы және аса маңызды кезеңі математикада функция ұғымының анықтамасы болды. Тіпті терең болғанына қарамастан функционалдық тәуелділік туралы идеялар ежелгі дәуірлерде айтылып басталған. Бастапқыда функция ұғымының интерпретациясы тек геометриялық немесе болды механикалық: ерікті қисық нүктелерінің ординаталары-абциссалардың функциялары немесе жол мен жылдамдық уақыттың функциялары болып табылады. Сонымен қатар, сол уақытта Готфрид Лейбниц келесі терминдерді енгізді “функция” латын тілінен аударылған “орындау”, “ айнымалы”, “тұрақты” дегенді білдіреді. Кейіннен, біраз уақыт бойы аналитикалық көзқарас басым бола бастады функцияны интерпретациялау, яғни анықтаушы формуламен функцияны сәйкестендіру, белгілеу алғаш рет енгізілді. Сонымен ғасыр функция ұғымының самодержавиеден азат болуымен сипатталады формулалар бірнеше жылдар дан кейін жасалған жиындар теориясының кеңеюіне көмектесті.
Генетикалық интерпретациясының негізі функция түсінігі болып табылады. Тұжырымдамаға кіретін қағидалар мен қасиеттерді әдістемелік өңдеу ғасырдың ортасына дейін қызмет етті.
Қолданылатын негізгі ұғымдар генетикалық интерпретация мыналарды қамтиды: ауыспалы, айнымалылардың функциялық тәуелділігі, декарттық жүйе жазықтықтағы координаталар. Бұл тәсілдің артықшылықтары мыналарды қамтиды концепцияның динамикалық сипатын көрсетіп функция ұғымының модельдік аспектісін анықтау.
Функция ұғымының логикалық түсіндірмесі негізделген әдістемелік талдау-мұндағы функция қатынастың ерекше түріне айналады функционалдық шартты қанағаттандыратын екі жиын арасында. Оқыту студенттердің «көзқарас» ұғымымен танысуынан басталады - жұмыс барысында әртүрлі иллюстрациялық материалдар пайдаланылады.
Тәуелділіктер алуан түрлі ғылымдардың және сан түрлі пәндерде қолданылады. Мектеп курсында берілген ұғымды қарастыру оқушылардың осы ұғымды оқыған кезінде маңыздылығын және шын өмірде қолданысын көріп, ұғымның зерттелетін жерде көп заңдар мен байланыстар негізі бар екенін көруге мүмкіндік береді.
Алгебра курсында ұғымын оқытуға көп көңіл бөлінген. Оқушылардың осы ұғымды түсінуі математикалық білінің негізі болып табылады.
Оқуты жүйесі ұғымды қалыптастыру үшін оның компонентері бөлек-бөлек сыныптарда қарастырып, содан кейін олардың арасындағы байланыс құрастырылған. Жоғары сыныптарда оқытылатын материалдарға дайындау мақсатында кіші сыныптардан бастап функция ұғымын саналы түрде қалыптастырылады.
Жалпы міндеттеріне көшетін болсақ, біріншіден функция ұғымын түсіну, яғни басты мақсат шәкірттерге функция ұғымын
1. 2 Алгебра оқулықтарындағы «Функция» тақырыбының мазмұнын талдау
5 сынып математикасындағы айнымалысы бар өрнектерді оқып үйрену функцияны оқып үйренуге дайындық болып табылады. Мұнда «функция» термині енгізілмейді, алайда осы ұғымды қалыптастыру жөнінде жыл бойы жүйелі түрде жұмыс жүргізіледі. Функция ұғымының қалыптасуына айнымалы шамалары бар арифметикалық есептерді шығаруға көмектеседі. 5 сыныптағы функционалдық түсініктерді қалыптастыру жөнінде басталған жұмыс 6 сыныпта функцияны «тәуелділік» деген ұғым арқылы оқытылады.
Ал 7-сыныпта функция ұғымын енгізуге мүмкіндік береді, функция ұғымының мазмұны айқындалып, тиісті анықтама беріледі. Функцияның берілу тәсілдері (таблицалық, графиктік, аналитикалық) қарастырылады.
функциясын оқып үйренеді. Осы функцияның графигі салынады. Сызықтық функцияның анықтамасымен танысып, пен функцияларының графиктерімен танысады.
Функция ұғымының өте үлкен көлеміне, кеңдігіне және күрделілігіне қарамастан, оның қарапайым нұсқасы мектептің орта сыныптарында қазірдің өзінде берілген. Бұл концепция алгебраны оқытуде және талдаудың бастауларында негізгі ұғым бола отырып, болашақта маңызды рөл атқарады. Жалпы білім беретін мектептің 7-сыныбынан бастап функциялардың қасиеттері мен функционалдық тәуелділіктерді кезең-кезеңімен меңгерту қолға алынған. Функциялардың әртүрлі кластары қарастырылады: ең қарапайым сызықтық функциялардан және олардың графиктерінен бастап, содан кейін квадраттық функциялар, кері пропорционалдық функциялар және сызықтық бөлшек функциялар.
8-сыныпта функциялық түсініктер дамытылады. Мысалы, бүтін теріс көрсеткіші бар дәрежелерді оқығанда түріндегі функциялардың графиктері, квадрат түбірлерді оқығанда функциясының графигі, квадрат теңдеулерді оқығанда квадрат үшмүшеліктердің графиктері қарастырылады.
8-сыныптың соңында сандық теңсіздіктердің қасиеттерін зерттегеннен кейін ғана функцияның монотондылығына қатаң формалды анықтама беріледі, яғни монотондылық жалпы деңгейде оқытылады.
8-сыныптың басында Квадраттық функция ұғымын зерттей отырып, егер функцияның графигі Ох осіне параллель кейбір түзудің астында орналасса, онда функция жоғарыдан шектелген деп аталады. Егер функцияның графигі Ох осіне параллель кейбір сызықтан жоғары болса, онда функция төменнен шектелген деп аталады (сурет 1) . Функцияның шектелуі туралы мұндай түсінік визуалды-интуитивті болып табылады.
8-сыныптың соңында осы қасиеттің формальды деңгейде көрсетілуін қолдана отырып, жоғарыдан және төменнен шектелген функцияның ауызша көрінісі қолданылады. Егер функцияның барлық мәндері белгілі бір саннан аз болса, онда бұл функция жоғарыдан шектелген деп аталады. Әйтпесе, функция төменнен шектеледі.
9-сыныптағы жалпылау деңгейінде функцияның төменнен шектелу қасиетін оқыту анықтаманы енгізуді қамтиды: y = f(x) функциялары (f) жиынында төменгі жағынан шектелген деп аталады, егер x жиынындағы функцияның барлық мәндері белгілі бір саннан үлкен болса (басқаша айтқанда, егер сан болса) т кез келген мән үшін осындай орындалады теңсіздік f (x) >т) . Жоғарыдан шектелген функцияға ұқсас.
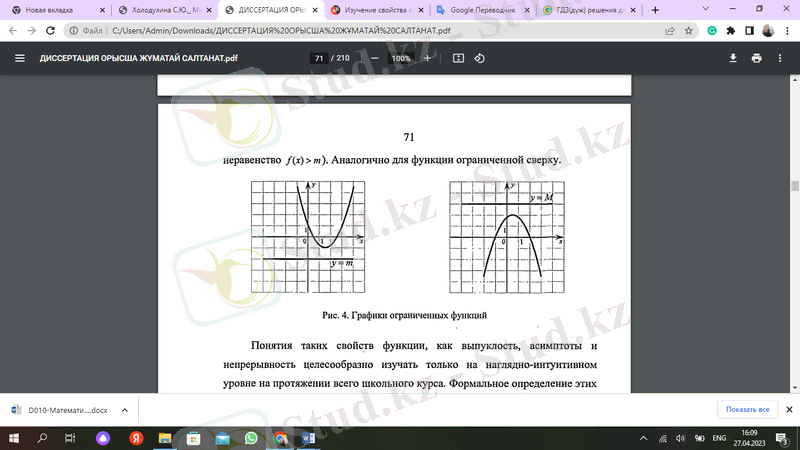
Сурет 1. Шектеулі функция графиктері
9-сыныпта оқылатын алгебра курсында функцияларды оқып-үйрену әрі қарай жалғастырылады. Берілген функцияға кері функция ұғымы енгізіледі.
Қазіргі кезде мектептерге арналған көптеген эксперименттік оқулықтар бар. Біз зерттеу тақырыбы бойынша негізгі мектепте қолданыстағы Алгебра оқулықтарына талдау жүргізейік.
А. Е. Әбілқасымова, Т. П. Кучер, В. Е. Корчевский, З. Ә. Жұмағұлова авторларының 7 сынып «Алгебра» оқулығының үшінші тарауы «Функция және оның графигі» деп аталынады. Бұл оқулықта тараудың әрқайсысынан кейін автор қайталауға арналған жаттығулар мен өз бетінше шешуге арналған тапсырмалар береді. Барлық ұсынылған тапсырмалар 3 бөлікке бөлінеді: А деңгейіндегі тапсырмалар, В деңгейіндегі тапсырмалар және С деңгейіндегі күрделі тапсырмалар. Ұзақ мерзімді жоспарға сәйкес функция тарауына 10 сағат берілген. «Функция» тарауы он бөлімнен тұрады.
«Функция және оның графигі» тарауында функцияны формула арқылы беру, функцияны кестемен беру тәсілі, функцияны графикпен беру тәсілі, сызықтық функция және оның графигі, сызықтық функция графиктерінің өзара орналасуы, екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу, квадраттық функция қасиеттері, графигі, кубтық функция, функцияның мәндер жиынын табу, таңбатұрақтылығын табу .
Тарау «Функция» тақырыбынан басталады. Бұл тақырыпта оқушылар функционалдық тәуелділік, аргумент, анықталу аймағы, функция ұғымымен, функцияның өспелі және кемімелі болатындығымен танысады.
Функция ұғымына төмендегідей анықтама берілген:
Анықтама: х айнымалысының әрбір мәніне у айнымалысының бір ғана мәні сәйкес болғанда у айнымалысының х айнымалысына тәуелділігі функция деп аталады.
Оқушыларға мысалдар беріліп, сол мысалдар арқылы жаңа ұғымдар түсіндірілген.
Мысалы, y=30x функциясы үшін айнымалының мүмкін болатын мәндер жиыны кез келген сан, сондықтан анықталу аймағы сан аралығы болады; функциясы үшін айнымалының мүмкін мәндер жиыны нөл санынан басқа барлық сандар, сондықтан анықталу аймағы - сан аралығы.
Тақырып бойынша үш мысал қарастырылған, оқушыларға практикалық бөлім бойыншажалпы тоғыз есеп берілген. Оқулықта қайталау мен жаңа тақырыпты меңгеруге есептер берілген.
Тараудың екінші тақырыбы «Функцияны формула арқылы беру». Тақырып функцияны беру ұғымымен таныстырудан басталады. Функцияны формула арқылы берілетіні туралы анықтама жазылған:
Функцияны формула арқылы беру функцияны аналитикалық тәсілмен беру деп аталады.
Жалпы тақырыпта жеті мысал есеп берілген. Практикалық бөлімде тоғыз есеп және қайталау есебі, жаңа тақырыпты меңгеруге арналған есептер берілген.
Келесі тақырып «Функцияны кестемен беру тәсілі». Бұл тақырыпта кестенің қалай толтыруы керектігі жайлы, анықталу аймағын табуға үйрету қарастырылған. Кесте бойынша функцияның өспелі немесе кемімелі екенін анықтауды үйреткен.
Тараудың үшінші тақырыбы «Функцияны графиктік тәсілмен беру». Функцияны график арқылы, яғни координаталар жиыны арқылы беруге болады. Бұл жиын шексіз және шектелген, яғни бірнеше нүктеден тұруы мүмкін. Бұл нүктелердің абсциссалары тәуелсіз айнымалыға, ал ординаталары тәуелді айнымалыға тең.
Тақырыпта алты мысал көрсетілген. Практикалық бөлімде он есеп берілген. Жаңа білімді меңгеруге арналған есеп берілген.
Келесі тақырып «Сызықтық функция және оның графигі». Ең бірінші сызықтық функцияның анықтамасымен басталған.
Анықтама. y=kx+b формуласымен (x-тәуелсіз айнымалы, k және b-қандай да бір сандар) беруге болатын функцияны сызықтық функция деп атайды.
Мысалы, -сызықтық функциялар.
Координаталары арқылы график, кесте салу кезең-кезеңімен көрсетілген.
Сызықтық функцияның графигін салу үшін, екі нүкте белігілеп, олар арқылы түзу жүргізу керек екендігі айтылады(9-сурет)
Тақырыпта төрт мысал есеп, он төрт практикалық есеп берілген.
«Сызықтық функциялар графиктерінің өзара орналасуы» тақырыбында сызықтық функция графиктерін қалай анықтауға болатындығы түсіндірілген.
y=kx+b формуласымен берілген сызықтық функциялардың графиктері x-тің коэффициенттері әртүрлі болғанда қиылысады; x-тің коэффициенттері бірдей болғанда параллель; x-тің коэффициенттері тең және b сандары бірдей болғанда беттеседі.

9-сурет-сызықтық функция графигі
Демек, кез келген y=kx+b сызықтық функциясы координаталары (0; b) болатын нүкте арқылы өтеді. Бұл тақырыпта он төрт есеп бар.
«Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу» тақырыбында тәсілмен шығарудың алгоритмі құрылған.
Екі айнымалысы бар теңдеулер жүйесін графиктік тәсілмен шығарғанда мына алгоритм қолданылады:
- бір координаталық жазықтықта әр теңдеудің графигін салу;
- теңдеулер графиктерінің қиылысу нүктесінің (егер қиылысатын болса) координаталарын табу;
- жүйенің жауабын айнымалылардың мәндерінің жұбы түрінде жазу.
Бұл тақырыпта үш мысал үлкен көлемде түсіндіріліп, әрбір қадамы көрсетілген. Практикалық есептер саны тоғыз.
Ендігі тақырып « функциясы, оның қасиеттері және графигі». Функцияның жалпы қасиеттері берілген. Символдық түрде қалай белгіленуі көрсетілген. Қасиеттеріне тоқталатын болсақ:
- a>0 болғанда функция графигі І және ІІ ширектерде;
- a<0 болғанда функция графигі IIIжәне IVкоординаталық ширектерде орналасады.
- x-тің(−∞; 0) ⋃(0; +∝) аралығындафункцияa>0болғандаоңмәндер, a<( - \infty; 0) \bigcup(0; + \propto ) аралығында\ функция\ a > 0\ болғанда\ оң\ мәндер, \ a < 0\ болғанда\ \ теріс\ мәндер\ қабылдайды
Параболаның графигін анықтамасымен түсіндірген:
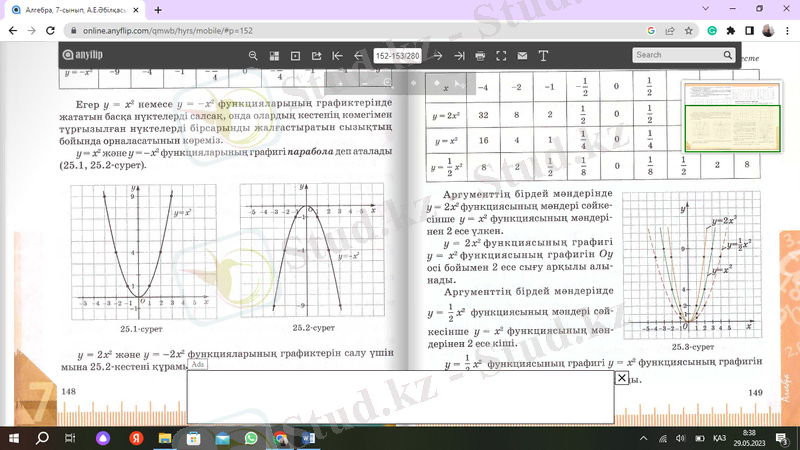
10-сурет-парабола графиктері
Тақырып соңында өзіндік жұмысқа арналған тапсырмалар бар. Практикалық есептер саны он. Жаңа тақырыпты меңгеруге арналған тапсырма берілген.
« функциясы, оның қасиеттері және графигі» тақырыбында функцияның негізгі қасиеттері және ол қалай салынуы керектігі жайлы жазылған.
мәндерінің жиыны сан осі деп аталады.
Бұл тақырыпта функцияны кезең кезеңімен анықталу облысы, мәндер облысы, таңба тұрақтылықтарын, функцияның нөлдерін табуды көрсеткен. Ол оқушыларға өте ыңғайлы болып табылады. Тақырыпта он бір практикалық есеп берілген.
Келесі тақырып « функциясы, оның қасиеттері және графигі». функциясының қасиеттеріне тоқталайық:
- y=kx(k≠0) y = \frac{k}{x}(k \neq 0) функциясының анықталу аймағы нөлден өзге барлық сандар жиыны болады, демек(−∞; 0) ⋃(0; +∞) ( - \infty; 0) \bigcup(0; + \infty)
- k>0k > 0\болғандаy=kxy = \frac{k}{x}функциясының мәндер жиыны(−∞; 0) ⋃(0; +∞) ( - \infty; 0) \bigcup(0; + \infty) аралығында болады.
- Функцияның таңбатұрақтылық аралығын табамыз.
k>0 болғанда функция ) аралығында оң мәндерді, аралығында теріс мәндерді;
k<0 болғанда функция аралығында оң мәндерді, ) аралығында теріс мәндерді қабылдайды.
- Функция нөлдері:y=kx(k≠0) y = \frac{k}{x}(k \neq 0) функциясы нөлге тең емес. Бұл функцияның графигі Ox осін қиып өтпейтінін көрсетеді.
- Функцияның өсу және кему аралықтарын табады.
функцияларының барлығының графиктері гипербола деп аталады.
Практикалық есептер саны он бір. Тақырып соңында жаңа білімді меңгеруге арналған есептер бар. Тараудың соңында оқушыларға өтілген тақырыптарды жақсы меңгеріп, естеріне түсіру үшін «Өзіңді тексер!» шығармашылық тапсырмасы берілген.
А. Е. Әбілқасымова, И. Бекбоев, А. Абдиев, З. Ә. Жұмағұлова авторларының 8-сынып «Алгебра» оқулығының бірінші тарауы «Квадрат түбірлер» деп, ал үшінші тарауы «Квадраттық функция» деп аталынады. «Квадрат түбірлер тарауында» бір ғана тақырып функцияға берілген, яғни бір сағат. Ал «Квадраттық функция» тақырыбында үш тақырып, алты сағат берілген. Барлық ұсынылған тапсырмалар 3 бөлікке бөлінеді: А деңгейіндегі тапсырмалар, В деңгейіндегі тапсырмалар және С деңгейіндегі күрделі тапсырмалар.
« функциясы және оның графигі» тақырыбында оқушылар, оның қасиеттері, және графигімен танысып, есептерді шығару кезінде функцияның қасиеттерін қолдана алады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz