Ауданның өлшем бірлігі ретінде квадрат алынады, оның жағы сегменттердің өлшем бірлігіне тең

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Қазақстан Республикасының Ғылым және жоғарғы білім
министірлігі
А.Байтұрсынұлы атындағы Қостанай өңірлік университеті
Мектепке дейінгі және бастауыш білім беру кафедрасы

КУРСТЫҚ ЖҰМЫС

Тақырып: Аудан. Құрама фигуралардың ауданы

Пән: Бастауыш мектепте математиканы оқыту әдістемесі
білім беру бағдарламасы: 6В01301 Бастауышта оқыту педагогикасы мен әдістемесі

Орындаған: Жакыпова А.А. күндізгі оқу нысанының 1 курс студенті

Ғылыми жетекші: п.ғ.магистрі,аға оқытушы Кушмурзина Д.Х.

Курстық жұмыс қорғауы
болған күні ___ _______20__ж
Бағасы_____________________

Қостанай, 2024
МАЗМҰНЫ

Кіріспе 3
1
Аудан теориясының негіздері
5
1.1
Аудан ұғымының даму тарихы және оның өлшемдері
5
1.2
Аудан теориясының негіздері
8
2
Практикалық бөлім
12
2.1
Аудандармен жұмыс кезеңдері
12
2.2
Құрама фигуралардың ауданы міндеттердің негізгі функциялары және оларды бастауыш сыныптарда оқыту процесінде іске асыру әдістемесі
14
Қорытынды
18
Әдебиеттер тізімі
20

КІРІСПЕ

Құрама фигуралардың ауданын зерттеу және ауданын есептеу бастауыш мектеп математика курсының негізгі тақырыптарының бірі болып табылады. Ол қарапайым математикалық дағдыларды қалыптастырып қана қоймайды, сонымен қатар кең ойлауды, логикалық ойлауды және практикалық есептерді шешу дағдыларын дамытады. Ауданды беттің сандық сипаттамасы ретінде түсіну және әртүрлі фигуралардың ауданын есептеу мүмкіндігі күнделікті өмірде және болашақ білім беру жолдарында қолданылатын маңызды дағдылар болып табылады.
Бұл курстық жұмыс ауданға қатысты негізгі ұғымдарды, құрама фигуралардың ауданын есептеу әдістерін және осы тақырыпты бастауыш мектепте оқыту тәсілдерін қамтиды. Күрделі фигураларды қарапайым бөліктерге бөлу, әр бөліктің ауданын есептеу және нәтижелерді шығару әдістеріне ерекше назар аударылады. Оқытудың әртүрлі әдістерін, соның ішінде көрнекілік, технология және ойындарды қолдану оқушыларға материалды жақсы түсінуге және есте сақтауға көмектеседі. Практикалық жаттығулар мен топтық жұмыстарды енгізу де білімді тереңірек түсінуге және сақтауға ықпал етеді.
Сонымен қатар, фигураның ауданын квадрат миллиметр, квадрат километр, квадрат метрмен өлшейді.
Бастауыш мектепте құрама фигуралар аймағын зерттеудің өзектілігі бірнеше факторларға байланысты:
1. Практикалық қолдану: Өмірде біз еденді төсеу үшін бөлменің ауданын өлшеу немесе жер учаскесінің көлемін бағалау болсын, ауданды есептеуді қажет ететін тапсырмаларды жиі кездестіреміз.
2. Математикалық дағдыларды дамыту: Аймақты оқу аналитикалық қабілеттерін дамытуға, сандармен және формулалармен жұмыс істеуге ықпал етеді.
3. Әрі қарай оқуға дайындық: Геометрия мен алгебра негіздерін түсіну орта және жоғары мектепте тереңдетілген математикалық түсініктерді табысты меңгеру үшін өте маңызды.
Бұл курстық жұмыстың мақсаты - әртүрлі әдістер мен тәсілдерді қолдана отырып, бастауыш мектепте құрама фигуралар аймағы тақырыбын қалай тиімді оқытуға болатынын көрсету. Жұмыста теориялық аспектілер, практикалық тапсырмалардың мысалдары, сонымен қатар табысты оқу және студенттерді ынталандыру стратегиялары қарастырылады.
Сонымен, ауданды зерттеу және оны құрама фигуралар арқылы есептеу математиканы одан әрі табысты меңгеруге негіз қалап, бастауыш математикалық білімнің маңызды бөлігі болып табылады.

1 Аудан теориясының негіздері

1.1 Аудан ұғымының даму тарихы және оның өлшемдері

Аудандарды өлшеуге байланысты геометриялық білімнің пайда болуы мыңжылдықтардың тереңдігінде жоғалады.
Тағы 4-5 мың жыл бұрын вавилондықтар тіктөртбұрыш пен трапеция тәрізді жер учаскелерінің аудандарын шаршы бірліктермен есептеген. Ауданның өлшем бірлігі ежелгі заманнан бері квадратты қолданған, өйткені бұл керемет қасиеттерге ие квадрат: тең жақтары, тең және тік бұрыштары; квадраттың осі мен симметрия орталығы және форманың жетілдірілуі бар. Квадраттарды салу оңай және оларды кез-келген пішіндегі фигураның бос жерлерінсіз жабуға болады.
Шамамен 4000 жыл бұрын мысырлықтар тіктөртбұрыштың, параллелограммның, үшбұрыштың және трапецияның ауданын біз сияқты әдістермен анықтады. Яғни, тіктөртбұрыштың ауданын анықтау үшін ұзындығын еніне көбейтті; үшбұрыштың ауданын табу үшін үшбұрыштың табаны екіге бөлініп, биіктікке көбейтілді. Трапецияның ауданын табу үшін параллель жақтардың қосындысы екіге бөлініп, биіктікке көбейтілді. Көпбұрыштың ауданы оны тіктөртбұрыштарға, үшбұрыштарға және трапецияларға бөлу арқылы табылды.
Мысырлықтар басқаларын да қолданды, бұл жер учаскесінің ауданын тек шекаралар бойынша айналып өту арқылы тезірек өлшеуге мүмкіндік берді, бірақ өлшеу нәтижесі кейбір қателіктермен алынды. Сонымен, изоссельді үшбұрыштың ауданы формула бойынша есептелді

S=,

мұндағы а-бүйір жағы, b-үшбұрыштың негізі. Бұл жағдайда қате неғұрлым аз болса, соғұрлым жақын болады бұрышы а және b жақтары арасында.
Қазіргі формуладан бастап,

S= а::b

мұны б=млы:4; а=млы:3 , S=. Мысырлықтар төртбұрыштың ауданын есептеу үшін де abcd формуласын пайдаланды,

S= . .

Осы формула бойынша төртбұрыштардың ауданын есептеу кезінде қате жіберілді. Төртбұрыштың бұрыштары түзуге жақын болған кезде ол минималды болады. Ал тіктөртбұрыш жағдайында нәтиже дәл болады, өйткені формуладан

Күрделі түрде, SABCD= AB+CD . AB=CD және AD=BC кезінде AD+BC
біз аламыз

SABCD= 2AB. 2AD = AD.

Ал параллелограмм жағдайында бұл формула нақты қателік береді.
Параллелограммдардың ауданының Египет формуласына сәйкес, біз АД қабырғаларында салынған тіктөртбұрыштардың тең аудандарын аламыз. Көлеңкеленген аудандар екі түрлі жағдайда параллелограмның ауданын анықтауда жіберілген қатенің шамасын көрсетеді. Егер параллелограммның СВА бұрышы түзу сызықтан алыс болса, онда қате шамалы болуы мүмкін.
Евклид, Герон, Брахмагупта және басқалардың математикалық жазбаларында аудандарды өлшеу мәселелері бойынша гректер мен индустар мысырлықтар мен вавилондықтармен салыстырғанда әлдеқайда алға жылжығаны белгілі. Евклид өзінің бастауларында аудан сөзін қолданбаған, өйткені ол фигура сөзімен белгілі бір тұйық сызықпен шектелген жазықтықтың бір бөлігін түсінеді және фигура ұғымы оның ауданын да білдіреді. Евклид ауданды өлшеу нәтижесін санмен білдірмейді, әр түрлі фигуралардың аудандарын бір-бірімен салыстырады. Евклид сонымен қатар сандармен емес, аудандармен жұмыс жасай отырып, белгілі бір фигураларды олардың тең бөліктеріне айналдыру мәселелерімен айналысады.
Үнді математигі Брахмагупта (598 - 660) төртбұрыштың ауданын есептеу үшін ұқсас формуланы шығарғысы келді. Егер біз төртбұрыштың ауданын белгілесек S, оның жарты периметрі арқылы р, ал жақтары арқылы а, b, с және d, содан кейін Брахмагупта қабылдады S= р(р-а)(р-b)(р-с)(р-d), бірақ дәлелденбеген.
Брахмагупт формуласы тіктөртбұрышқа қатысты, өйткені тек тіктөртбұрыштарда р-а=b және р-b = а. Сондықтан
Брахмагупт формуласы кез-келген төртбұрыш үшін дұрыс емес. Ол теңбүйірлі трапеция үшін және диагональдары өзара перпендикуляр шеңберге жазылған төртбұрыштар үшін қолданылады. Брахмагуптаның өзі формуласын қолдануда абай болды және оны тек көрсетілген фигуралардан жоғары аудандарды анықтау үшін қолданды. Оның формуласы кез - келген төртбұрыштың ауданының нақты мөлшерінің шамамен мәнін ғана бергенімен, жер учаскелерінің аудандарын өлшеуді жеңілдетті, өйткені периметр бойынша сайтты айналып өту және оны өлшеу қарапайым міндет.
Фигуралардың аудандарын қиылысатын түзулердің көмегімен бөлу және алынған бөліктерден жаңа фигураларды кесу және қайта құру арқылы бір фигураны екінші фигураға айналдыру міндеттері грек математиктерін қызықтырды, өйткені жерлеу және сәулет жұмыстары осындай мазмұндағы міндеттерді алға тартты.
Египет пен Үндістанның ежелгі математиктері кейбір ерекше жағдайларда дұрыс аудандарды есептеу ережелерін жалпы жағдайға негізсіз ауыстырды. Ресейде XI-XVI ғасырлар да ережелерді жалпылау жолымен жүрді. XVI ғасырдың екінші жартысында жерді өлшеуге, артиллерия ісінің дамуына және қалалардың құрылысына деген қажеттіліктің артуы геометриялық мазмұндағы қолжазбалар жасау қажеттілігіне әкелді. 1551 жылы патша Иван IV адамдарды мемлекетті сипаттау және өлу үшін жіберді. Өкінішке орай, ежелгі Ресейдің қолжазбалары бізге жеткен жоқ. Ежелгі заманнан бері орыс тарихының авторы В.Н. Татищев (1686-1750) былай деп жазды: Мен 1556 жылы жазушыларға жерді қалай өлшеу керектігі туралы берілген бұйрықты оқыдым. Тапсыпмада жер сызбалары, яғни сызбалар қосылды. Тапсырма із-түзсіз жоғалып кетті. Жазушы және тарихшы Н.М. Карамзиннің (1766 - 1826) отбасында сақталған XVII ғасырдың математикалық қолжазбалары да жоғалып кетті.
Аудандарды өлшеу ережелерін сипаттайтын қолжазбалардың біріншісі-1629 жылға жататын ең көне көшірме - Соқалардың хаты кітабы, дегенмен түпнұсқаның 1556 жылы Иван Грозныйдың тұсында жасалғаны туралы нұсқаулар бар. Бұл кітапта жер бетіндегі жер туралы тарауы бар. Өкінішке орай, аудандарды өлшеу әдістерінде көптеген қате материалдар бар. Олар қолмен қайта жазу кезінде бұрмаланудың нәтижесінде пайда болуы мүмкін.
Сонымен, аудан (s) - жазықтықтың жазық жабық фигураның ішінде орналасқан бөлігінің өлшемін сипаттайтын шама.
Геометриялық фигуралардың аудандарын анықтау-ежелгі практикалық міндеттердің бірі. Оларды шешудің дұрыс тәсілі бірден табылмады.
Әр жазық геометриялық фигураның өзіндік ауданы бар. Кеңістіктік фигуралардың беткі ауданы деп аталатын тиісті ауданы да бар.
Фигураның ауданын өлшеу дегеніміз-оны ауданның өлшем бірлігі ретінде қабылданған кейбір фигураның ауданымен салыстыру.
Ежелгі Грециядағы фигураның ауданын өлшеу дегеніміз-ауданы берілген фигураның ауданына тең шаршы салу. Содан бері ауданды есептеу әдетте квадратура деп аталады.
Аудандарды өлшеу кесінділердің ұзындығын өлшеуге ұқсас таңдалған өлшем бірлігі арқылы жүзеге асырылады. Ауданның өлшем бірлігі ретінде квадрат алынады, оның жағы сегменттердің өлшем бірлігіне тең. Сонымен, егер ұзындық бірлігі үшін сантиметр қабылданса, онда ауданы өлшем бірлігі үшін 1 см квадрат қабылданады. Мұндай квадрат шаршы сантиметр деп аталады және см2 деп белгіленеді. Егер ұзындықтың өлшем бірлігі 1 м болса, оған 1 м2 аудан бірлігі сәйкес келеді, егер 1 мм болса, онда аудан бірлігі 1 мм2.
Мысалы, ауданның өлшем бірлігі ретінде шаршы сантиметр қабылдансын. Содан кейін s =15 см2 жазбасы фигураның ауданы 15 см2 екенін білдіреді, яғни бұл фигурада 1 см жағы бар шаршы 15 рет салынады. Әдетте, торлы қағаздағы тапсырмаларда тор шартты түрде шаршы сантиметр ретінде қабылданады.

1.2 Аудан теориясының негіздері

Көпбұрыштың ауданын анықтаудан бастайық. Қарапайым көпбұрыш жазықтықтың онымен шектелген бөлігімен бірге қарапайым жабық сынық деп аталады. Біз қарапайым көпбұрыштарды ғана қарастырамыз, оларды қысқаша көпбұрыштар деп атаймыз.
Көпбұрыштардың аудандарын табу тақырыбы әрқашан көптеген ұлы математиктердің санасын толғандырды. Евклид өзінің бастауларында аудан сөзін қолданбаған, өйткені ол фигура сөзінің өзі жазықтықтың бір немесе басқа тұйық сызықпен шектелген бөлігін түсінген. Евклид әртүрлі фигуралардың аудандарын бір-бірімен салыстырды. Ежелгі басқа ғалымдар сияқты, Евклид кейбір фигураларды басқаларына айналдыру мәселелерімен айналысқан, олар оларға тең. Құрама фигураның ауданы, егер оның бөліктері басқаша орналасса, өзгермейді, бірақ қиылысусыз. Сондықтан, мысалы, тіктөртбұрыштың аудан формулаларына сүйене отырып, басқа фигуралардың аудан формулаларын табуға болады.
Анықтама: Евклид жазықтығындағы барлық көпбұрыштардың m жиынын қарастырыңыз. Егер келесі аксиомаларды қанағаттандыратын S : M--R+ картасы анықталса, көпбұрыштардың аудандарын өлшеу орнатылады деп айтылады:
1. Егер a және b көпбұрыштары тең болса, онда S(a)=S(b).
2. Егер ab=a+b болса, онда S(ab)=S(a)+S(b).
3. S (d)=1 , мұндағы P0 - бүйір сияқты бірлік сегментке салынған шаршы.
S(a) оң саны F көпбұрышының өлшемі немесе ауданы, P0 квадраты бірлік квадрат, ал 1, 2 және 3 аксиомалары аудандарды өлшеу аксиомалары деп аталады.
Бастауыш сынып бағдарламасы бойынша:
1-Теорема: (болмыс және бірегейлік): евклидтік геометрияда әрдайым 1, 2 және 3 аксиомаларын қанағаттандыратын S : M--R+ картасы болады, ал егер Бірлік сегменті таңдалса, онда бұл карта жалғыз болады.
Салдары: a көпбұрышын үшбұрыштардың ақырлы жиынына ыдыратудың кез келген әдісімен осы үшбұрыштардың аудандарының қосындысы бірдей.
Мысалы, a көпбұрышының ауданын есептеу үшін оны үшбұрыштарға бөліп, алынған үшбұрыштардың аудандарының қосындысын алайық. Үшбұрыштарға бөлудің әртүрлі әдістерімен біз бірдей нәтиже алатынымыз анық. Бірақ неге? Мектеп геометриясында бұл сұраққа жауап жоқ. Болмыс пен бірегейлік теоремасы нақты жауап береді: көпбұрыштың кез-келген бөлінуінде a үшбұрыштар, олардың аудандарының қосындысы S(a) ерекше анықталған санын береді. Осы теоремадан, сондай-ақ аудан аксиомаларынан кез-келген тіктөртбұрыштың, параллелограммның, үшбұрыштың ауданын есептеу формулалары алынады.
2-Теорема: егер S: 1, 2 және 3 аксиомаларын қанағаттандыратын карта болса, онда S (a)=xy, мұндағы P - қабырғалары х және b болатын тіктөртбұрыш.
3-Теорема: егер S: 1, 2 және 3 аксиомаларын қанағаттандыратын карта болса, онда S (ab)=ab мұндағы a - Үшбұрыш, b - оның қабырғаларының бірі, ал y - сәйкес биіктік.
Анықтама: егер олардың аудандары тең болса, екі көпбұрыш тең деп аталады.
Тепе-теңдік барлық көпбұрыштардың b жиынындағы эквиваленттік қатынас екені анық.
Анықтама: екі a және b көпбұрыштары, егер оларды сәйкесінше тең көпбұрыштардың бірдей санына бөлуге болатын болса, эквивалентті деп аталады.
Эквиваленттік қатынас барлық көпбұрыштардың b жиынындағы эквиваленттік қатынас екенін дәлелдеуге болады.
4-Теорема: егер көпбұрыштар тең болса, онда олар тең болады.
Ескерту: бұл теорема a көпбұрышының ауданын есептеу кезінде ыдырау әдісіне негізделген: бұл көпбұрыш көпбұрыштардың ақырлы жиынына ыдырайды, олардан ауданы белгілі көпбұрышты "бүктеуге" болады. Осылайша, мектеп геометрия курсында параллелограмм, Үшбұрыш, трапеция ауданын есептеу формулалары табылды.
Келесі тұжырым 4-Теоремаға кері болып табылады.
5-Теорема (бояй-Гервин): егер көпбұрыштар тең болса, онда олар тең болады.
Осылайша, барлық көпбұрыштардың a жиынында теңдік қатынасы теңдік қатынасымен сәйкес келеді.
Ерікті фигураның ауданымен, мысалы, шеңбердің ауданымен қалай болуға болады? Бұл мәселе мектеп геометриясының материалын ұсыну кезінде де туындайды. Осы уақытқа дейін жазықтықтың барлық көпбұрыштарының жиынтығы ғана болған аймақ теориясының зерттелетін саласын кеңейту қажеттілігі туындайды.
6-Теорема:барлық квадратталған фигуралардың жиынтығында бар, сонымен қатар 1, 2 және 3 аксиомаларын қанағаттандыратын s функциясы бар.
S(a) саны a фигурасының ауданы деп аталады, мұндағы a-квадратталған фигура.
Ескерту: бүкіл фигураны біртіндеп толтыратын көпбұрыштарды қарастыруға негізделген фигураның ауданын есептеу әдісі сарқылу әдісі деп аталады (мектеп оқулықтарында шеңбердің ауданын есептеу формуласы осы әдіспен шығарылады).
Палетканы қолдану туралы (аудандарды тікелей өлшеу).
Әдетте a фигурасының S(a) ауданы бұл фигураның қанша аудан бірлігінен жасалғанын көрсететін сан деп айтылады (квадрат аудан бірлігі үшін алынады, оның жағы ұзындық бірлігіне тең). Алайда, мұндай көрнекі түсініктеме аудан ұғымының нақты математикалық анықтамасы бола алмайды. Мысалы, берілген радиустың шеңбері аудан бірліктерінен қалай жасалатыны белгісіз.
Аудан ұғымын анықтаудың бір әдісі палитраны қарастыруға негізделген-жазықтықты сәйкес квадраттарға бөлу. Палитраның бүйірінің ұзындығы 1 болсын. a фигурасы берілсін және ab фигурасындағы квадраттардың ең үлкен саны, ал b1-осы фигураны қамтитын квадраттардың ең аз саны. Мысалы, a фигурасында палитраның 9 квадратынан тұратын және 29 квадраттан тұратын фигура бар, сондықтан 9 = S (a) = 29, яғни a1=9, b1=29 (сурет 1).

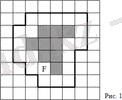
Сурет 1. 9 квадратынан тұратын және 29 квадраттан тұратын фигура

Дәлірек бағалау үшін палетканы қолдануға болады, оның квадраттарының ұзындығы 10 болатын жақтары бар (сондықтан бұрынғы палитраның әр квадратында жаңа палитраның 100 квадраты болады). Егер, айталық, F құрамында жаңа палитраның 1716 квадратынан тұратын фигура болса және осындай 1925 квадраттан тұратын фигурада болса, онда 17,16 = s=25. Тағы да, палитраны ұсақтау арқылы (яғни квадраттардың бүйірлерінің ұзындығын 10 есе азайту арқылы) біз S (a) және т. б.
Сипатталған өлшеу процесі тек ауданды табу үшін ғана емес, сонымен қатар аудан ұғымын анықтау үшін де қолданылады. Дәлірек айтқанда, квадраттардың бүйірлерінің ұзындығы 25 болатын палитраны қарастырайық. A құрамында осы палитраның ak квадраттарынан жасалған және осындай квадраттардың bk-дан жасалған фигурада болсын(мысалы, бізде a2=1716, b2=1925 жоғары). Содан кейін ak102k - бұл F фигурасының ауданының мәні, кемшілігі бар, ал bk102k-артық деп айтуға болады.
Егер фигура осы шектермен сәйкес келсе, онда фигурасы квадрат деп аталады. Қарастырылған шектердің бұл мәні a фигурасының ауданы деп аталады және S(a) арқылы белгіленеді.
Жоғарғы және төменгі аймақтар сәйкес келмейтін фигураға мысал келтіру қиын емес. Осы мақсатта 1 ауданының квадратынан ауданы 4-тен аз крестті алып тастаймыз (сурет 2, а). Содан кейін қалған төрт квадраттың әрқайсысында біз барлық төрт кресттің аудандарының қосындысы 8-ден аз болатындай етіп крестті алып тастаймыз (сурет 2, б). Содан кейін біз жалпы ауданы 16-дан аз 16 крестті алып тастаймыз және т. б. кресттерді алып тастаудың шексіз санынан кейін қалатын фигураны Q арқылы белгілейміз.
Сондықтан қалған Q фигурасын 12 аудан фигурасына орналастыру мүмкін емес, яғни Q фигурасының жоғарғы ауданы 12-ден үлкен. Сонымен қатар, Q фигурасында ешқандай квадрат жоқ (ол қаншалықты кішкентай болса да), сондықтан фигураның төменгі ауданы нөлге тең. Осылайша, фигураның жоғарғы және төменгі аймақтары сәйкес келмейді, яғни Q фигурасы квадратталмаған.

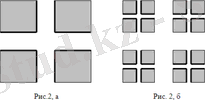
Сурет 2 а және б

Бұл мысал аудан ұғымы кез-келген фигураға қолданылмайтындығын көрсетеді. Дегенмен, кез келген көпбұрыштың квадратталған фигура екенін дәлелдеуге болады. Сол сияқты, кез-келген дөңес фигура (атап айтқанда шеңбер) квадратталады. Жалпы, квадратталған фигуралар класы өте кең.
Енді s аудандарын өлшеу барлық квадратталған фигуралар класында берілген және сандық мәндерді қабылдайтын функция деп айтуға болады, яғни әрбір a фигурасының S(a) ауданы теріс емес сан болып табылады (аудан бірлігі бекітілген деп есептеледі).
Ауданның осы анықтамасын қолдана отырып (палитралардың көмегімен) ауданның бірқатар қасиеттерін дәлелдеуге болады...
Біздің аудандарды табу мәселелерін зерттеудің нағыз асыл тастары-бұл шыңның формуласы. Жүз жыл бұрын неміс математигі Георг Пик көпбұрыштың ауданын есептеудің керемет формуласын ашты және дәлелдеді. Шың формуласы дөңес полиэдрдің шыңдары, шеттері мен беттерінің санын байланыстыратын әйгілі Эйлер формуласымен байланысқан.

S = B + Г2-1
Жалпы, мектепте палитраны қолданған кезде мыналарды есте сақтау пайдалы екенін атап өткім келеді:
1. Ауданды палеткамен өлшеу тікелей (тікелей) өлшем болып табылады, онда шаманың қажетті мәні оны тиісті бірлікпен салыстыру арқылы анықталады. Кесінділердің ұзындығын өлшеу және формулаларды қолдану арқылы ауданды өлшеу жанама болып табылады. Тікелей салыстыруды жанама салыстырумен ауыстыру адам ойының маңызды жетістігі болып табылады және ежелгі математикалық абстракциялардың бірін білдіреді. Бұл абстракция оқушыға оңай беріледі деп болжауға негіз жоқ, істің мәнін түсінбеу аудандарды өлшеу теориясын одан әрі зерттеуді едәуір қиындатады (бұл, ең болмағанда, қабырғалардың ұзындығы натурал сандармен көрсетілмеген жағдайда, тіктөртбұрыштың ауданы формуласының негіздемесін білдіреді). Шынында да, кез-келген формула бойынша сегменттердің ұзындығын есептеуге үйретпес бұрын, біз сегменттерді тікелей өлшеуге үйретеміз және осылайша есептеулерді
тікелей өлшеу арқылы тексеруге мүмкіндік береміз. Аудан тақырыбында палеткамен жұмыс осы бастапқы кезеңге сәйкес келеді.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.