Комбинаторика: ұғымы, элементтері және қолданылуы


Қазақстан Республикасының Оқу Ағарту Министрлігі
облысы, қаласы
жалпы орта мектебі
Ғылыми жоба
Тақырыбы:Комбинаторика ұғымы және оның элементтері
Орындаған:
Ғылыми жетекші:
2024-2025 оқу жылы
МАЗМҰНЫ:
I. КІРІСПЕ.
II. НЕГІЗГІ БӨЛІМ.
1. Комбинаторика ұғымы
2. Комбинаториканың шығу тарихы
3. Комбинаторика элементтері
III. ПРАКТИКАЛЫҚ БӨЛІМ
IV. ҚОРЫТЫНДЫ.
V. ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР.
Аңдатпа.
Зерттеудің өзектілігі: Біздің өмірімізге сайлау мен референдумдар, банк несиелері мен сақтандыру полистері, жұмыспен қамту кестелері мен әлеуметтік сауалнамалар диаграммалары кірді. Қоғам өзін тереңірек зерттеп, өзі туралы және ықтималдық туралы түсініктерді талап ететін табиғат құбылыстары туралы болжам жасауға ұмтыла бастады. Тіпті теледидар мен газеттер бойынша әлемдік нарықтардағы валюта болжамының мәліметтері ертең 5% баға белгіленімдерінің төмендеуі күтілуде деп хабарлайды. Әрине, бұл теорияның пайда болуы ғылымда кездейсоқ құбылыс болды ма?
Зерттеу жұмысының ғылыми болжамы: егер біз өмірімізде жиі кездесетін комбинаторикалық есептерді шешудің тиімді жолдарын біліп алсақ, онда нақты жағдайлар мен оқиғалардың мүмкін болатын дамуының көп нұсқалығына, жеке тұлғаны қалыптастыруға, қиын, үнемі өзгеріп тұратын әлемде өмір сүру және жұмыс істеу қабілетіне оңай дағдылана алар едік.
Ғылыми жұмысының максаты: әртүрлі типтегі және шешу әдістері мен тәсілдерінің алуан түрлілігі кезінде комбинаторлық есептерді шешудің жалпы тәсілдерін анықтау, математиканы зерттеуге тұрақты қызығушылықты дамыту, негізгі типтегі есептерді, аралас түрдегі есептерді, күрделілігі жоғары есептерді шешу әдістерін меңгеру.
Ғылыми жұмысының міндеттері:
1) әдебиетті зерттеу және талдау;
2) комбинаторлық есептерді шешу тәсілдерін іздеу;
3) комбинаторлық есептерді шешу;
4) комбинаторлық есептер банкін құру.
Ғылыми жұмысының ғылыми жаңалығы. Бұл зерттеу қоршаған ортаға басқаша қарауға көмектеседі. Оны зерделеп, математикалық есептеулерге сүйене отырып, кейбір нәрселерді объективті бағалай аламын.
Жұмыс қорытындысы. Күнделікті өмірде комбинаторлық әдістерді көптеп қолдануға болады.
Зертеудің теориялық және практикалық маңызы: комбинаторикалық есептердің түрлі жолдары қарастырылды. Комбинаторикалық есептеулерді тұрмыста, және математика сабақтарында қолдануға болады.
Жұмыстың орындалу әдістері. Зерттеу мәселесі бойынша оқу-әдістемелік әдебиетті зерттеу және талдау; салыстыру, қорыту және жіктеу әдістері; теориялық-әдістемелік материалдарды жинақтау және талдау.
Аннотация.
Актуальность исследования: мы впервые на уроках математики встречались с интересными задачами - коммбинаторикой, относящимися к одной из разделов математики. Комбинаторные задачи могут ответить на многие вопросы, связанные с практической деятельностью людей, решение задач помогает развивать умственные способности, логическое мышление, вычислительные навыки. Знание комбинаторики необходимо для представителей разных профессий. С комбинаторными обязанностями приходится вести делопроизводство физиологам, лингвистам, специалистам по теории кодов.
Научный прогноз исследовательской работы: если мы узнали эффективные пути решения наиболее часто встречающихся комбинаторических задач в нашей жизни, то мы могли бы легко привыкать к многообразию возможного развития конкретных ситуаций и событий, формированию личности, способности жить и работать в трудном, постоянно изменяющемся мире.
Цель научной работы: определение общих способов решения комбинаторских задач при различных типах и разнообразии способов и методов решения, развитие устойчивого интереса к изучению математики, овладение методами решения задач основного типа, комбинированных задач, задач повышенной сложности.
Задачи научной работы:
1) изучение и анализ литературы;
2) поиск способов решения комбинаторных задач;
3) решение комбинаторских задач;
4) создание банка комбинаторских отчетов.
Научная новизна научной работы. Это исследование поможет другим взглянуть на окружающую среду. Изучив его, опираясь на математические расчеты, могу объективно оценивать некоторые вещи.
Итоги работы. В повседневной жизни можно использовать много комбинаторных методов.
Теоретическое и практическое значение исследования: рассматривались различные пути комбинаторских задач. Комбинаторические расчеты можно использовать в быту и на уроках математики.
Методы выполнения работ. Изучение и анализ учебно-методической литературы по проблемам исследования; методы сравнения, обобщения и классификации; сбор и анализ теоретико-методических материалов.
Abstract.
Relevance of the study: for the first time in mathematics lessons we met with interesting problems-combinatorics related to one of the branches of mathematics. Combinatorial problems can answer many questions related to the practical activities of people, problem solving helps to develop mental abilities, logical thinking, computational skills. Knowledge of combinatorics is necessary for representatives of different professions. With combinatorial duties have to keep records physiologists, linguists, specialists in the theory of codes.
Scientific forecast of research work: if we learned effective ways to solve the most common combinatorial problems in our lives, we could easily get used to the variety of possible development of specific situations and events, the formation of personality, the ability to live and work in a difficult, constantly changing world.
Objective of research: determine the General solutions combinatorica tasks in different types and variety of ways and methods of solving, the development of a sustainable interest in learning mathematics, mastering the methods of solving tasks of the basic type, the combined challenges of increased complexity.
Tasks of scientific work:
1) study and analysis of literature;
2) finding ways to solve combinatorial problems;
3) solving combinatorial problems;
4) creating a Bank of combinatorial reports.
Scientific novelty of scientific work. This research will help others look at the environment. Having studied it, relying on mathematical calculations, I can objectively assess some things.
Result of work. Many combinatorial methods can be used in everyday life.
Theoretical and practical significance of the study: different ways of combinatorial problems were considered. Combinatorial calculations can be used in everyday life and in mathematics lessons.
Methods of work. Study and analysis of educational and methodical literature on research problems; methods of comparison, generalization and classification; collection and analysis of theoretical and methodological materials.
КІРІСПЕ.
Біздің өмірімізге сайлау мен референдумдар, банк несиелері мен сақтандыру полистері, жұмыспен қамту кестелері мен әлеуметтік сауалнамалар диаграммалары кірді. Қоғам өзін тереңірек зерттеп, өзі туралы және ықтималдық туралы түсініктерді талап ететін табиғат құбылыстары туралы болжам жасауға ұмтыла бастады. Тіпті теледидар мен газеттер бойынша әлемдік нарықтардағы валюта болжамының мәліметтері ертең 5% баға белгіленімдерінің төмендеуі күтілуде деп хабарлайды. Әрине, бұл теорияның пайда болуы ғылымда кездейсоқ құбылыс болды ма?
Математиканың маңызды және елеулі бөлімдерінің бірі комбинаторика болып табылады. «Комбинаторлық өнермен» әр адам таныс болу керек. Комбинаторлық месептердің шешу техникасын меңгерген, демек, ойлай білетін, шешімнің әр түрлі нұсқаларын таңдай білетін адамдар жиі қиын жағдайлардан шығу жолын тауып кетеді. Мұны үйрену үшін зерттеу қызметімен айналысу керек, яғни зерттеу, шешу, тану керек.
Комбинаторика біздің өмірімізде қайда қолданылады?
• білім мекемелерінде (сабақ кестесі) ;
•Тамақтану орындарында (тамақ мәзірін жасауда) ;
•Спорттық жарыстарда;
•Агротехникада;
•Географияда;
•Химия;
•Биология;
•Экономика;
•Криптография (шифрларды теру әдістерінде) кездеседі екен.
Зерттеудің өзектілігі: Біз математика сабағында бірінші рет математикасының бір бөліміне жататын қызықты есептермен - коммбинаторикамен кездестік. Комбинаторлық есептер адамдардың практикалық қызметімен байланысты көптеген сұрақтарға жауап бере алады, есептерді шешу ақыл-ой қабілеттерін, логикалық ойлауды, есептеу дағдыларын дамытуға көмектеседі. Комбинаториканы білу әр түрлі мамандық өкілдеріне қажет. Комбинаторлық міндеттермен физиологтарға, лингвистерге, кодтар теориясы бойынша мамандарға іс жүргізуге тура келеді.
Комбинаториканың даму тарихын зерделей отырып, біз ғалымдардың осы саланы қалай дамытқанын және осы атаудыбергенін ұғынам. Осының бәрі тұлғаның жан-жақты дамуы үшін қажет. Қазіргі заманның иесі жақсы математикалық дайындыққа ие болуы және өз білімі мен дағдыларын тәжірибеде қолдана білуі тиіс. Осы мақсатта біз комбинаторика мен оның дамуы туралы көбірек білуді шештік.
Мен ықтимал жағдайда өмір сүруді үйрену керек. Бұл дегеніміз ақпаратты алу, талдау және өңдеу, кездейсоқ нәтижелермен әр түрлі жағдайларда негізделген шешімдер қабылдау. Нақты жағдайлар мен оқиғалардың мүмкін болатын дамуының көп нұсқалығына, жеке тұлғаны қалыптастыруға, қиын, үнемі өзгеріп тұратын әлемде өмір сүру және жұмыс істеу қабілетіне дағдылану менің өскелең ұрпақ сияқты ықтималды - статистикалық ойлауды дамытуды талап етеді.
Мен таңдаған зерттеу тақырыбының өзектілігі комбинаторлық міндеттерді шешу кезінде білімді тереңдету қажеттілігінен туындап отыр.
Жұмыстың мақсаты - әртүрлі типтегі және шешу әдістері мен тәсілдерінің алуан түрлілігі кезінде комбинаторлық есептерді шешудің жалпы тәсілдерін анықтау, математиканы зерттеуге тұрақты қызығушылықты дамыту, негізгі типтегі есептерді, аралас түрдегі есептерді, күрделілігі жоғары есептерді шешу әдістерін меңгеру.
Зерттеудің негізіне комбинаторлық есептерді шешу жалпы ықтималдық теориясын түсіну мен қабылдауды жеңілдететіні туралы болжам алынған.
Қойылған мақсаттарды іске асыру және ұсынылған болжамды тексеру үшін зерттеудің келесі міндеттерін шешу қажет:
1) әдебиетті зерттеу және талдау;
2) комбинаторлық есептерді шешу тәсілдерін іздеу;
3) комбинаторлық есептерді шешу;
4) комбинаторлық есептер банкін құру.
Қойылған міндеттерді шешу барысында келесі зерттеу әдістері қолданылды:
1) Зерттеу мәселесі бойынша оқу-әдістемелік әдебиетті зерттеу және талдау;
2) салыстыру, қорыту және жіктеу әдістері;
3) теориялық-әдістемелік материалдарды жинақтау және талдау.
2. 1 Комбинаторика ұғымы
Комбинаторика-бұл математиканың саласы, онда белгілі бір шарттарға бағынатын қанша түрлі комбинацияларды осы жиынтыққа жататын элементтерден құруға болатындығы туралы сұрақтар зерттеледі.
Комбинаторика XVI ғасырда пайда болды. Сол кездегі қоғамның артықшылықты топтарының өмірінде құмар ойындар (карталар, сүйектер) үлкен орын алды. Лотереялар кең таралды. Бастапқыда комбинаторлық тапсырмалар негізінен құмар ойындарға қатысты болды: берілген ұпай санын 2 немесе 3 сүйек лақтыру арқылы қанша жолмен алуға болады немесе кейбір карточкалық ойындарда 2 Патшаны қанша жолмен алуға болады. Құмар ойындардың осы және басқа да мәселелері Комбинаториканың дамуындағы және одан әрі ықтималдық теориясының дамуындағы қозғаушы күш болды.
"Комбинаторика "сөзі латынның" combinare "сөзінен шыққан, орыс тіліне аударғанда - "қосу", "біріктіру" дегенді білдіреді. Комбинаторлық міндеттер дойбы, шахмат, домино, карталар, сүйектер және т. б. сияқты ойындарға байланысты туындады. "Комбинаторика" терминін 1666 жылы әлемге әйгілі неміс ғалымы Готфрид Вильгельм Лейбниц енгізген.
Комбинаторика (лат. Combino - жалғастырамын) - комбинаторикалық анализ деп те аталады. Комбинаторикалық анализ комбинаторикалық математика, комбинаторика - математиканың кез келген шектеулі жиын (шектеудің кейбір шарттарын шексіз жиын) бөліктерінің орналастырылуы мен өзара орналасуына байланысты мәселелерін зерттейтін бөлімі.
Алғашқылардың бірі болып итальяндық математик Тартаглия ойнаған кезде әртүрлі комбинациялардың санын есептей бастады. Ол кестелерді құрастырды (R сүйектеріне k ұпай жинау тәсілдерінің саны) . Алайда, ол ескермеді, ұпай саны бірдей болуы мүмкін, сондықтан оның кестелерінде көптеген қателер болды.
Комбинаторика мәселелерін теориялық зерттеуді XVII ғасырда француз математиктері Блез Паскаль және Ферма жүргізді. Олардың зерттеулерінің бастапқы нүктесі құмар ойындар проблемалары болды.
Комбинаториканың одан әрі дамуы я. Бернулли, г. Лейбниц, Л. Эйлер есімдерімен байланысты. Алайда, олардың жұмысында әр түрлі ойындарға қосымшалар басты рөл атқарды.
Бүгінгі таңда комбинаторлық әдістер көлік мәселелерін шешу үшін қолданылады, атап айтқанда кесте құру, өндіріс жоспарларын құру және өнімді сату және т. б.
Комбинаторикалық сипаттағы идеялар ықтималдық теориясы, алгебра тәрізді математикалық бөлімдерінде өте кең тараған. Комбинаторикалық анализ есептері ерте кезден - ақ белгілі болған. Оның дамуына көптеген математиктер елеулі үлес қосты. Бірақ комбинаторикалық анализ өз алдына пән ретінде тек 20 ғасырда ғана қалыптаса бастады. Комбиторикалық графтар теориясы, шектеулі автоматтар теориясы тәрізді математиканың салаларымен тығыз байланысты. Оның тәжірибелері ғылыми тәжірибелерді жоспарлауды және оларға талдау жасауда, сызықтық және динамикалық бағдарламалауда, математикалық экономикада, т. б. ғылым мен техникалық көптеген салаларында қолданылады. Комбинаторикалық анализ проблемасының үш түрі бар.
Санап шығу есептерінде объектілердің шектеулі жиынынды кездесетін шарттарды қанағаттандыратын орналастырулар саны қарастырады. Іс жүзінде мұндай есептер жасаушы функциялар әдісі мен Д. Пойаның (1887-1985) (американдық математик) санап шығу әдісінің көмегімен шешіледі.
Салу есептерінде кейбір қасиеттері сақталатын шектеулі жиын бөліктері конфигурациясының болуы, егер болса оның салынатындығы туралы мәселелер қарастырылады. Таңдап алу есептерінде ішкі жиын бөліктерінің кейбір құрамын таңдап алу шарттары зерттеледі. мұндай есептерді шешкенде комбинаторлық ойлармен қатар алгебралық аппарат та қолданылады.
Дискреттік математика - математиканың дискретті құрылымдардың қасиеттернін зерттейтін саласы. Мұндай құрылымдарға шектеулі топтар, шектеулі графтар, сондай-ақ, ақпаратты түрлендіргіш кейбір математикалық модельдер шектеулі автоматтар, Тьюринг машинасы, т. б. жатады. Бұлар шектеулі сипаты бар құрылымдар болып есептеледі. Дискретті математиканың шектеулі құрылымдарды зерттейтін бөлігін шектеулі математика деп атайды. Дискреттік математикада, жоғарыда аталған шектеулі құрылымдармен бірге, кейбір алгебралық жүйелер, шексіз графтар белгілі бір түрлері есептеу сұлбалары, т. б. зерттеледі. «Дискреттік математика» және «шектеулі математика» ұғымдарының синонимі ретінде кейде «дискреттік талдау» термині қолданылады.
Комбинаторлық міндеттер бөлінеді: пермутациялық тапсырмалар, орналастыру міндеттері, біріктіру тапсырмалары. Анықтама: факторлық-бұл 1-ден n-ге дейінгі барлық натурал сандардың көбейтіндісі.
2. 2 Комбинаториканың шығу тарихы
Комбинаторлық деп аталатын міндеттерге адамдар ежелгі уақытта тап болған екен. Бірнеше мыңжылдықтар бұрын Ежелгі Қытайда сиқырлы квадраттарды құрастыруға қызығушылық танытты, онда берілген сандар олардың барлық көлденең, тік және негізгі диагональдардағы қосындысы бірдей болатындай етіп орналастырылды.
Ежелгі Грецияда олар поэтикалық өлшемдегі ұзын және қысқа сөздердің әртүрлі комбинацияларының санын санады, фигуралық сандар теориясымен айналысты, арнайы кесілген квадраттың бөліктерінен құрастыруға болатын фигураларды зерттеді және т. б. комбинаторлық есептер дойбы, шахмат, домино, карталар, сүйектер және т. б. сияқты ойындарға байланысты пайда болды.
Комбинаториканы бірінші болып әлемге әйгілі неміс ғалымы Готфрид Вильгельм Лейбниц ғылымның дербес саласы ретінде қарастырды.
1666 жылы Лейбниц "комбинаторлық өнер туралы пайымдаулар"жариялады. Лейбниц өзінің жазбасында арнайы таңбаларды, терминдерді енгізе отырып, n элементтерінің барлық k-комбинацияларын табады, комбинациялардың қасиеттерін шығарады, комбинация кестелерін жасайды, содан кейін Комбинаториканың логикаға, арифметикаға, верификация мәселелеріне және т. б. қосымшалары туралы айтады.
XVIII ғасырда көрнекті математиктер комбинаторлық есептерді шешуге бет бұрды. Комбинаторика саласындағы керемет жетістіктер Леонард Эйлерге тиесілі. Ол сандарды бөлу, циклдік орналасу, сиқырлы және латын квадраттарын құру мәселелерін қарастырды. 1713 жылы Я. Бернуллидің шығармасы жарық көрді, онда сол уақытқа дейін белгілі комбинаторлық фактілер жеткілікті түрде баяндалды. Комбинаторлық есептерге шифрларды құрастырумен және шешумен, ежелгі жазбаларды зерттеумен айналысатын математиктер де қызығушылық танытты. Енді комбинаторика ғылымның көптеген салаларында қосымшаларды табады: биологияда, ол белоктар мен ДНҚ құрамын зерттеу үшін қолданылады, химияда, күрделі құрылымдардың механикасында және т. б. физика, химия, биология, экономика және басқа ғылымдардың комбинаторлық міндеттері, бұрын есептеулердің күрделілігіне байланысты шешілмеген, компьютерлерде сәтті шешіле бастады. Нәтижесінде комбинаторлық зерттеу әдістері ғылым мен техниканың көптеген салаларына тереңірек енуде. Атап айтқанда, компьютердің көмегімен төрт бояу мәселесі шешілді: кез-келген картаны төрт түске бояуға болатындығы дәлелденді, сондықтан ортақ шекарасы бар екі ел бірдей түске боялмайды.
1844 жылы Дж. Сильвестр: "Сан, позиция және комбинация - бұл бір-бірімен қиылысатын үш, бірақ барлық математикалық идеяларды жатқызуға болатын әртүрлі ой салалары", - деді.
2. 3 Комбинаториканың қолданылуы
Комбинаторика бойынша білімді пайдалану өте маңызды, оларсыз күнделікті өмірде жасау мүмкін емес. Қарапайым комбинаторлық есептеулермен көптеген мамандықтардың өкілдері айналысуы керек: әр түрлі жұмыс түрлерін жұмысшылар арасында бөлу кезінде прораб, қозғалыс кестесін құру кезінде диспетчер, оқу сабақтарының кестесін құра отырып, мектеп меңгерушісі әртүрлі комбинацияларды қолданады.
Көптеген ғылымдарда комбинаторика туралы Білім қолданылады. География (карталарды бояу), лингвистика (әріптер комбинациясының нұсқаларын қарастыру), агротехника (дақылдарды бірнеше өрістерге орналастыру), химия (химиялық элементтер арасындағы ықтимал байланыстарды талдау), экономика (акцияларды сатып алу-сату нұсқаларын талдау), биология (ДНҚ кодын декодтау), астрология (планеталар мен шоқжұлдыздардың орналасуын талдау) және т. б.
Комбинаторлық Білім көптеген ойындарда жеңіске жету үшін қолданылады. Комбинаторика шахмат ойнау кезінде ерекше маңызға ие. Ең жақсы қозғалысты табудың негізгі әдісі-мүмкін болатын қимылдарды асыра пайдалану, ағаш бойынша қозғалысты дәйекті позицияларды қарастыру және олардан туындайтын ойын күйлерін бағалау. Опцияларды санау үшін ойнатқыш көп уақыт жұмсауы керек, сондықтан компьютерлік шахматтағы ең тиімді алгоритмдерді іздеу кезінде мүмкіндігінше көп шектеулер (шарттар) ескерілуі керек, бұл кезекті таңдағанда қарастырудың қажеті жоқ позицияларды алып тастауға мүмкіндік береді.
Біздің бүкіл өміріміз көптеген түрлі бағдарламалардан тұрады. Осы немесе басқа Бағдарламаны іске қосу үшін сізге тиісті құпия сөзді енгізу керек.
Бағдарламаның түріне байланысты Код ретінде барлық сандар, сөздер немесе сөз тіркестері, мінез-құлық немесе әрекет және т. б. болуы мүмкін . . . Сол бағдарлама қандай пароль ұсынылатынына байланысты ұсынылған парольге сәйкес әртүрлі тәсілдермен орындалады.
Комбинаторлық есептерді шешу туралы алған білімдерін қолдана отырып, сіз әрқашан жеңіске жететін комбинациялар бар екенін біле отырып, өмірді жеңілдете аласыз, таңдау бар!
Практикалық бөлімде Мен көлікке, саяхатқа қатысты мәселелерді шешу үшін комбинаторлық білімді қолдануды қарастырамын.
2. 4 Комбинаторика элементтері
Іс жүзінде кейбір заттардың өзара орналасуының барлық мүмкін жағдайлары санын, немесе қайсыбір әрекетіміздің барлық мүмкін нәтижелері санын есептеу, немесе оны орындаудың барлық мүмкін тәсілдері санын есептеу қажет болады. Мысалы, әр түрлі 5 оқулықты екі студент арасында неше түрлі тәсілмен үлестіріп беруге болады? Осындай есептерді комбинаторикалық есептер деп, ал комбинаторикалық есептерді оқып үйрететін матиматика саласын комбинаторика деп атайды. Комбинаторикалық есептерді шешу барысында қолданатын бірқатар заңдылықтар мен формулалар бар.
Комбинаторика есептерін шешкенде мына ережелер қолданылады.
Қосу ережесі - егер a элементін м тәсілімне, b элементін н тәсілмен таңдап алуға болса, а элементінің кез келген таңдауы b элемиентін таңдаудан өзгеше болса, онда а немесе b таңдауын m+n тәсілімен орындауға болады. Қосу ережесі. Егер А мен В объектілері тоғыспайтын болса және А объектісі m тәсілімен, ал В объектісі n тәсілімен алынса, онда
«А немесе В» объектілерін таңдау m + n тәсілмен жүзеге асады.
1-мысал . Математикадан оқушы ғылыми жобаны жазады. Оның таңдауына алгебрадан 17 тақырып, ал геометриядан -13 тақырып ұсынды. Қанша тәсілмен оқушы бір тақырыпты таңдай алады?
Шешуі: Қосынды ережесі бойынша 17+13=30 тәсіл.
Теорема: Кез келген санаулы элементтері бар А және В жиындары үшін
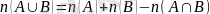 (1) теңдігі орындалады.
(1) теңдігі орындалады.
Салдар:Егер
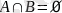 болса, онда
болса, онда
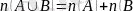 теңдігі орындалады.
теңдігі орындалады.
Дәлелдеу:
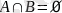 болғандықтан,
болғандықтан,
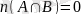 . Онда (1) формуладан көрсетілген теңдік шығады.
. Онда (1) формуладан көрсетілген теңдік шығады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz