Жартылай өткізгіштердің физикасы және диодтар мен транзисторлардың параметрлерін есептеу


Реферат
Научная работа включает: 33 страниц, 18 иллюстраций и 3 использованных литературных источников.
Объектами данной работы является полупроводники. Цель работы: анализ применения полупроводников в науке и технике. В основной части работы даны методы исследования физики полупроводников, полученные результаты, основные конструктивные, технологические и технико-эксплуатационные характеристики. На основе них сделаны соответствующие выводы. Представлена к рассмотрению программа нахождения параметров диодов и транзисторов. Анализ возможностей использования полупроводников показал, что полупроводники могут широко использоваться в различных электронных устройствах.
Мазмұны:
Кіріспе. . 3
1. Жартылай өткізгіштердің физикасы . . . 4
1. 1 Жартылай өткізгіштердің зона құрылымы. . 4
1. 2 Терминология және негізгі ұғымдар . . . 5
1. 3 Жартылай өткізгіштердегі электрондар мен тесіктердің статистикасы……6
1. 4 Доңғалақтар мен тесіктердің концепциясы . . . 11
1. 5 Ферми деңгейінің орналасуын анықтау12
1. 6 Жартылай өткізгіштердің өткізгіштігі . . . 13
1. 7 Жартылай өткізгіштердегі токтар14
1. 8 Теңгерімсіз тасымалдаушылар . . . 15
1. 9 Үздіксіздік теңдеуі17
2. Жартылай өткізгіш диодтары. 18
2. 1. p-n өтпесі негізіндегі идеалды диодтың сипаттамалары18
2. 2. Диодтағы түзету . . . 19
2. 3. Сипаттамалық кедергі . . . 19
2. 4. Диодтардың сипаттамаларына температураның әсері. 20
3. Транзисторлар. . 21
3. 1. Транзистордың жұмыс принципі22
3. 2. Цептің элементі ретінде транзистордың параметрлері. 23
3. 3. Транзисторлардың түрлері. . 25
3. 4. Биполярлық транзисторлардың технологиялық түрлері26
4. Диод пен транзистор параметрлерін есептеу бағдарламасы. . 27
Қорытынды32
Пайдаланылған әдебиеттер тізімі33
Кіріспе
Электроника - ғылым мен техниканың қарқынды дамып келе жатқан саласы. Ол түрлі электрондық құралдардың физикалық негіздерін және практикалық қолдануларын зерттейді. Физикалық электроникаға газдар мен өткізгіштердегі электрондық және иондық процестер, вакуум мен газ, қатты және сұйық денелер арасындағы шекаралардағы процестер жатады. Техникалық электроника электрондық құралдардың құрылымын және олардың қолдануын зерттейді. Электрондық құралдардың өндірістегі қолданылуына арналған сала «өнеркәсіптік электроника» деп аталады. Электроника мен радиотехниканың негізгі ұғымдарының бірі - «жартылай өткізгіш» ұғымы. Сондықтан бұл жұмыста біз осы ұғымның аясын қарастырамыз.
Жартылай өткізгіштер - бөлшектердің электр өткізгіштігі бөлме температурасында металдардың (10^6-10^4 Ом^-1 см^-1) және диэлектриктердің (10^-8-10^-12 Ом^-1) электр өткізгіштігі арасындағы аралық мәнге ие. Жартылай өткізгіштердің тән ерекшелігі - температураның жоғарылауымен электр өткізгіштігінің артуы; төмен температурада жартылай өткізгіштердің электр өткізгіштігі төмен болады; оған жарық, күшті электрлік өріс, жылдам бөлшектер ағындары және т. б. әсер етеді. Электр өткізгіштігінің қоспалар мен кристалдардағы ақауларға жоғары сезімталдығы да жартылай өткізгіштерге тән. Жартылай өткізгіштерге үлкен топтағы заттар (Ge, Si және т. б. ) жатады. Жартылай өткізгіштердегі заряд тасымалдаушылар - өткізгіштік электрондар мен тесіктер. Идеал кристалдарда олар әрқашан жұптармен пайда болады, сондықтан олардың концентрациялары тең. Реалды кристалдарда, құрамында қоспалар мен құрылым ақаулары бар, электрондар мен тесіктердің концентрациялары теңдік болмауы мүмкін және өткізгіштік негізінен тек бір типті тасымалдаушылар арқылы жүзеге асырылады (қараңыз: зона теориясы, қатты дене) . Жартылай өткізгіштердің ерекшеліктері олардың қолданылуын анықтайды (қараңыз: жартылай өткізгіш құралдар) . Барлық осы қасиеттер өткізгіштердің радиотехникада ең маңызды материалдардың бірі болуына мүмкіндік берді.
1. Жартылай өткізгіштердің физикасы
1. 1. Жартылай өткізгіштердің зоналық құрылымы
**Бора постулаттары бойынша** электрондардың энергетикалық деңгейлері изоляцияланған атомда дискретті мәндерге ие. Қатты дене - жеке атомдардың ансамблі, химиялық байланыс оларды кристалл торына біріктіреді. Егер қатты дене N атомынан тұрса, энергетикалық деңгейлер N-рет қайталанатын болады. Атом ядроларының электрлік өрісі бұзылу ретінде әрекет етіп, бұл қайталануды жояды. Қатты денені құрайтын атомдардың дискретті моноэнергетикалық деңгейлері энергетикалық зоналарға бөлінеді. Қатты денелердің энергетикалық зоналар құрылымын зерттегенде, күшті немесе әлсіз байланыс жақындатуында кванттық теңдеулердің шешімі бірдей сурет береді. Екі жағдайда да электрондар үшін рұқсат етілген және рұқсат етілмеген жағдайлар кезектесіп, рұқсат етілген зоналардағы электрондар саны атомдар санына тең болады, бұл рұқсат етілген зоналар ішінде энергетикалық деңгейлердің квазидискретті таралуы туралы айтуға мүмкіндік береді.
Қатты денелердің электрондық қасиеттері үшін ең маңызды рөлді жоғарғы және одан кейінгі рұқсат етілген энергетикалық зоналар атқарады. Егер олардың арасында энергетикалық алшақтық болмаса, онда мұндай зона құрылымы бар қатты дене металл болып табылады. Егер осы зоналар арасындағы энергетикалық алшақтық (әдетте рұқсат етілмеген зона деп аталады) 3 эВ-тен артық болса, онда қатты дене диэлектрик болып табылады. Ал, егер рұқсат етілмеген зона ширинасы Eg (0, 1 - 3, 0) эВ диапазонында болса, онда қатты дене жартылай өткізгіштер классына жатады. Қатты денені құрайтын атомдардың түріне және валентті электрондардың орбиталарының конфигурациясына байланысты кристалл торының әртүрлі типтері жүзеге асырылады, сондықтан энергетикалық зоналардың құрылымы да өзгереді.
Жартылай өткізгіштердегі жоғарғы, толық толтырылмаған энергетикалық зона «өткізгіштік зона» деп аталады. Одан кейінгі энергетикалық зона «валентті зона» деп аталады. Осы зоналар арасындағы рұқсат етілмеген жағдайлардың энергетикалық алшақтығы «рұқсат етілмеген зона» деп аталады. Зоналық диаграммаларда өткізгіштік зонаның түбі EC белгісімен, валентті зонаның шыңы EV белгісімен, ал рұқсат етілмеген зонаның ширинасы Eg белгісімен көрсетіледі.
Жартылай өткізгіштерде рұқсат етілмеген зонаның ширинасы кең диапазонда өзгеріп отырады, бұл олардың меншікті өткізгіштігін едәуір өзгертеді. Сондықтан жартылай өткізгіштер, бөлме температурасында σ меншікті электр өткізгіштігі 10^-8-ден 10^6 Ом⋅см-ге дейін болатын заттар ретінде жіктеледі, бұл өткізу түрі мен мөлшеріне, заттың құрылымына, температураға, жарыққа (радиация), электр және магнит өрістеріне және т. б. сыртқы жағдайларға байланысты. Диэлектриктер үшін рұқсат етілмеген зонаның ширинасы Еg > 3 эВ, меншікті өткізгіштігі σ < 10^-8 Ом⋅см, меншікті кедергі ρ = 1/σ > 10^8 Ом⋅см. Металдар үшін меншікті өткізгіштік σ > 10^6 Ом⋅см.
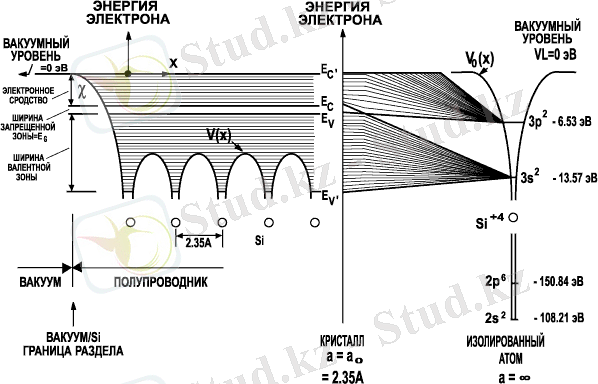
Сурет 1. 1. Изоляцияланған кремний атомындағы энергетикалық деңгейлер құрылымы, сондай-ақ, осы атомдардың жақындасуы кезінде пайда болатын монокристалдық кремнийдің энергетикалық зоналарының схемалық құрылымы
1. 2. Терминология және негізгі ұғымдар
Жартылай өткізгіштер , немесе жартылай өткізгіш қосылыстар, өзіндік және қоспалы болып табылады. Өзінің жартылай өткізгіштері - қоспалар (донорлар мен акцепторлар) жоқ жартылай өткізгіштер. Өздік концентрация ni - өзіндік жартылай өткізгіштегі заряд тасымалдаушылар концентрациясы (өткізгіштік зонадағы электрондар n және валентті зонадағы тесіктер p, мұнда n = p = ni) . T = 0 кезінде өзіндік жартылай өткізгіште бос тасымалдаушылар болмайды (n = p = 0) . T > 0 кезінде электрондардың бір бөлігі валентті зоннан өткізу зонасына лақтырылып шығарылады. Бұл электрондар мен тесіктер энергетикалық зоналарда еркін қозғала алады. Тесіктер - бұл толық толтырылмаған валентті зонадағы көптеген электрондардың (шамамен 10^23 см^-3) коллективті қозғалысын сипаттау тәсілі. Электрон - бұл бөлшек, ал тесік - бұл квазибөлшек. Электронды жартылай өткізгіштен немесе металдан сыртқа инжекциялауға болады (мысалы, фотоэффект арқылы), ал тесік тек жартылай өткізгіштің ішінде ғана болуы мүмкін.
Легирлеу - жартылай өткізгішке қоспа енгізу, бұл жағдайда жартылай өткізгіш қоспалы деп аталады. Егер 4-топ элементтерінен (мысалы, кремний немесе германий) тұратын жартылай өткізгішке 5-топ элементін енгізсе, донорлық жартылай өткізгіш (оның электрондық өткізгіштік типі болады), немесе n-типы жартылай өткізгіш алынады. Ал егер 3-топ элементін қоспа ретінде енгізсе, онда дыркалық өткізгіштікке (р-тип) ие акцепторлық жартылай өткізгіш алынады (сурет 1. 2) .
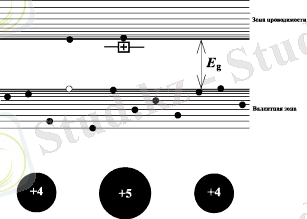
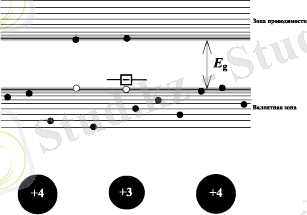
Рис. 1. 2. n-типы (а) және p-типы (б) жартылай өткізгіштердің энергетикалық схемалары
Жартылай өткізгіштердегі электрондар мен тесіктердің қозғалысын сипаттау үшін классикалық көріністерді қолдану үшін сәйкесінше тиімді Электрон массалары мен MN* және mp* тесіктері туралы түсініктер енгізіледі. Бұл жағдайда механика теңдеулері A = F/m* немесе dp/dt = F, егер бос электронның (вакуумдағы электронның) массасының орнына M0 осы теңдеулерге электронның тиімді массасын mn* (p = mn*·v) ауыстырса, дұрыс болады. Тиімді масса жартылай өткізгіш кристалындағы атомдардың периодтық потенциалының электрондар мен тесіктердің қозғалысына әсерін ескереді және дисперсия теңдеулерімен анықталады.
1. 3. Жартылай өткізгіштердегі электрондар мен тесіктердің статистикасы
Теңгерімдік процестер - сыртқы әсерлерге ұшырамайтын денелердегі процестер. Термодинамикалық тепе-теңдік күйінде берілген кристалл үлгісі үшін белгілі температурада электрондар мен тесіктердің энергияларға сәйкес бөлінуі және олардың концентрацияларының мәндері болады. Негізгі және қосымша заряд тасымалдаушылардың концентрацияларын есептеу электрондар мен тесіктер статистикасының басты міндетін құрайды.
Қарастырылып отырған тапсырма екі бөлікке бөлінеді: таза кванттық механикалық - электрондардың мүмкін кванттық жағдайларының санын анықтау, және статистикалық - термодинамикалық тепе-теңдік кезінде электрондардың осы кванттық жағдайларға нақты бөлінуін анықтау.
1. 3. 1. Аймақтардағы кванттық күйлердің таралуы
Идеал кристалдағы электронның стационарлық күйлері квази-импульспен сипатталады р. квази-импульстар үшін Гейзенберг гетерогенділігінің принципін жазайық dp x , dp y и dp z :
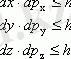 (1. 1)
(1. 1)
Осы қатынастардың сол және оң бөліктерін сәйкесінше көбейтейік. Біз аламыз
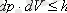 (1. 2)
(1. 2)
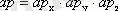 и
и
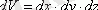 , яғни, dp-бұл px, py, pz квази-импульстік кеңістігіндегі белгілі бір көлем, яғни Бриллюен аймағының ішінде, ал dV - жартылай өткізгіштің ішіндегі белгілі бір көлем. Сонымен қатар, dV көлемі міндетті түрде шексіз шама емес. Бұл ақырғы болуы мүмкін. Заряд тасымалдаушылардың концентрациясын есептеу үшін (яғни жартылай өткізгіштің көлем бірлігіндегі тасымалдаушылар саны) Кристалл ішінде DV = 1 см3 бірлік көлемін бөлеміз. Содан кейін (1. 2) біз DP ≤ h3 аламыз. Яғни, Гауһар аймағында dp = h3 көлемінің ішінде тек бір кванттық күй болуы мүмкін, ол бүкіл көлемде бұлыңғыр болып көрінеді. Сонымен, h3-бұл Бриллюен аймағындағы бір "пәтердің" көлемі, оған әр түрлі спиндері бар екі электронды ғана орналастыруға болады және артық емес. Сондықтан бриллюин аймағындағы dp көлем элементіне сәйкес келетін және кристалл көлемінің бірлігіне есептелген кванттық күйлер саны dp/h3 - ге тең, яғни dp көлеміндегі "пәтерлер" саны. Өткізгіштік аймағын электрондармен толтырған кезде алдымен ең төменгі деңгейлер толтырылады. Өткізгіштік аймағы энергияға қатысты бір өлшемді (сурет. 1. 3 а) . Бриллюен аймағы - үш өлшемді (px, py, pz) (сурет. 1. 3 б) . Бриллюин аймағын толтыру квази-импульстің ең кіші мәндерінен басталады p. сондықтан dp ретінде екі өте жақын изоэнергетикалық беттер арасында орналасқан көлем элементін таңдау керек (суретті қараңыз. 1. 3 б) . Бұл жұқа шар қабатының ішінде радиусы P және қалыңдығы DP кванттық күйлер саны тең болады:
, яғни, dp-бұл px, py, pz квази-импульстік кеңістігіндегі белгілі бір көлем, яғни Бриллюен аймағының ішінде, ал dV - жартылай өткізгіштің ішіндегі белгілі бір көлем. Сонымен қатар, dV көлемі міндетті түрде шексіз шама емес. Бұл ақырғы болуы мүмкін. Заряд тасымалдаушылардың концентрациясын есептеу үшін (яғни жартылай өткізгіштің көлем бірлігіндегі тасымалдаушылар саны) Кристалл ішінде DV = 1 см3 бірлік көлемін бөлеміз. Содан кейін (1. 2) біз DP ≤ h3 аламыз. Яғни, Гауһар аймағында dp = h3 көлемінің ішінде тек бір кванттық күй болуы мүмкін, ол бүкіл көлемде бұлыңғыр болып көрінеді. Сонымен, h3-бұл Бриллюен аймағындағы бір "пәтердің" көлемі, оған әр түрлі спиндері бар екі электронды ғана орналастыруға болады және артық емес. Сондықтан бриллюин аймағындағы dp көлем элементіне сәйкес келетін және кристалл көлемінің бірлігіне есептелген кванттық күйлер саны dp/h3 - ге тең, яғни dp көлеміндегі "пәтерлер" саны. Өткізгіштік аймағын электрондармен толтырған кезде алдымен ең төменгі деңгейлер толтырылады. Өткізгіштік аймағы энергияға қатысты бір өлшемді (сурет. 1. 3 а) . Бриллюен аймағы - үш өлшемді (px, py, pz) (сурет. 1. 3 б) . Бриллюин аймағын толтыру квази-импульстің ең кіші мәндерінен басталады p. сондықтан dp ретінде екі өте жақын изоэнергетикалық беттер арасында орналасқан көлем элементін таңдау керек (суретті қараңыз. 1. 3 б) . Бұл жұқа шар қабатының ішінде радиусы P және қалыңдығы DP кванттық күйлер саны тең болады:
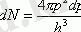 (1. 3)
(1. 3)
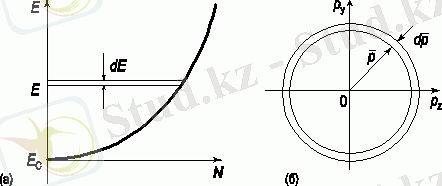
Сурет. 1. 3. Кванттық күйлердің тығыздығын есептеуге арналған Диаграмма:а-өткізгіштік аймағында электрондардың энергия бойынша таралуы; B-күй тығыздығын есептеуге арналған Бриллюэн аймағы
Кристалл көлемінің бірлігіне есептелген Е-ден Е+d-ге дейінгі энергияның тар интервалындағы өткізгіштік аймағындағы кванттық күйлердің санын анықтайық. Оны N(E) dE түрінде ұсынуға болады, мұндағы N(E) күйлердің тығыздығы.
Изотропты параболалық дисперсия Заңы үшін өткізгіштік аймағының түбіне жақын электрон энергиясы
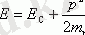 (1. 4)
(1. 4)
мұндағы ЕО-өткізгіштік аймағының түбіне сәйкес келетін энергия. Ыңғайлы болу үшін біз mn электронының тиімді массасын жұлдызшасыз жазамыз. (1. 4) біз аламыз
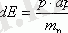 ,
,
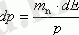 и
и
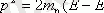 . (1. 3) ауыстырыңыз, бізде бар
. (1. 3) ауыстырыңыз, бізде бар
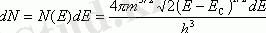 (1. 5)
(1. 5)
осыдан
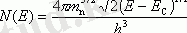 (1. 6)
(1. 6)
Ұқсас формула валенттік аймақ үшін де алынады, бірақ тек (Е - ЕО) орнына (ЕV - Е) жазамыз, ал mn орнына - MP тесігінің тиімді массасы.
(1. 6) - ден көрініп тұрғандай, өткізгіштік аймағының түбінен алыстаған сайын кванттық күйлердің тығыздығы артады.
1. 3. 2. Заряд тасымалдаушылардың концентрациясы және Ферми деңгейінің орналасуы
Электрондар, жартылай бүтін спині бар бөлшектер сияқты, Ферми-Дирак статистикасына бағынады. Электронның Е энергиясымен кванттық күйде болу ықтималдығы Ферми-Дирак функциясымен көрінеді:
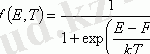 (1. 7)
(1. 7)
Мұнда F-электрохимиялық потенциал немесе Ферми деңгейі. (1. 7) - ден Ферми деңгейін толтыру ықтималдығы 1/2 болатын осындай кванттық күйдің энергиясы ретінде анықтауға болатындығын көруге болады.
Ферми-Дирак функциясының түрі 1. 4-суретте схемалық түрде көрсетілген. Т = 0 кезінде ол бұзылатын функция түрінде болады. E < F үшін ол 1-ге тең, яғни E < F кезіндегі барлық кванттық күйлер электрондармен толтырылған. E > F үшін f = 0 функциясы және сәйкес кванттық күйлер толығымен толтырылмаған. Т > 0 кезінде Ферми функциясы үздіксіз қисық сызықпен бейнеленеді және энергияның жоғары оқу орны, бірнеше kT реті бойынша, E = F нүктесінің маңында 1-ден 0-ге дейін тез өзгереді. Ферми функциясының бұлыңғырлығы температура неғұрлым жоғары болса.
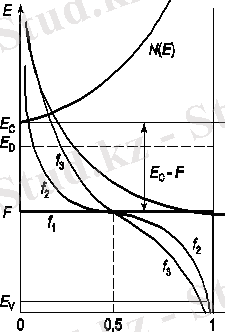
Сурет. 1. 4. N(E) өткізгіштік аймағындағы күй тығыздығының таралу функциясы, Ферми-Дирак F және Больцман fб функциялары
Әр түрлі статистикалық шамаларды есептеу, егер Ферми F деңгейі энергияның тыйым салынған аймағында жатса және ЕО аймағының шетінен кем дегенде 2kT қашықтықта болса (кейбір оқулықтарда ЕО - е > кт жазылады) айтарлықтай жеңілдетіледі. Содан кейін үлестірімде (1. 7) бөлгіштегі бірлікті елемеуге болады және ол классикалық статистиканың Максвелл - Больцман үлестіріміне өтеді. Бұл деградацияланбаған жартылай өткізгіштің жағдайы:
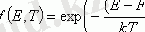 (1. 8)
(1. 8)
Өткізгіштік аймағындағы электрондардың концентрациясы:
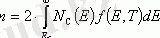 (1. 9)
(1. 9)
Жазбаша интегралдың жоғарғы шегі ретінде біз өткізгіштік аймағының жоғарғы жиегінің энергиясын алуымыз керек екенін ескеріңіз. Бірақ, E > F энергиялары үшін F функциясы E ұлғаюымен экспоненциалды түрде тез төмендейтіндіктен, жоғарғы шекті шексіздікке ауыстыру Интеграл мәндерін өзгертпейді. (1. 9) өрнектерін (1. 6) және (1. 8) ауыстырыңыз. Интегралды есептеу қиын емес. Біз аламыз
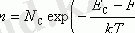 (1. 10)
(1. 10)
бұндп
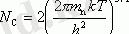 (1. 11)
(1. 11)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz