Максвеллдің қатынасы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

учебники, карандаши, лабораторное оборудование

Реферат

Максвелл қатынасы (термодинамика)

Серікқан Бағыжан

04. 10. 2024

Кіріспе

Сұрақтың тарихы

Максвеллдің арақатынасын шығару

Якобиандар арқылы жазу және қатынастарды шығару

Максвелл коэффициенттерін қолдану мысалдары

Максвеллдің күрделі термодинамикалық жүйелерге қатынасы

Ескертпелер

Әдебиеттер тізімі

Графическая карта мира

Максвеллдің қатынасы

(Максвеллдің термодинамикалық теңдеулері) - термодинамикалық шамалардың туындылары арасындағы бірдей қатынаста. Бұл математикалық сәйкестіктің салдары термодинамика- лық потенциалдың аралас туындыла- рының теңдігі. Қатынастар термодинамикалық формулаларды түрлендіру мақсатында математикалық есептеулерді орындау кезінде қолданылады. Олар термодинамика аппаратын едәуір кеңейтеді, өйткені олар эксперименталды түрде өлшенетін термодинамикалық шамаларды (мысалы, энтропия немесе химиялық потенциал) тікелей өлшеуге мүмкіндік бермейді.

Термодинамикаға 1871 жылы Джеймс Клерк Максвелл енгізген және оның есімімен аталады.

Сұрақтың тарихы

1871 жылы Кавендиш зертханасына жұмысқа орналасқанға дейін Максвелл газдардың кинетикалық теориясы мен электр энергиясы туралы монографиялар жазуға көп көңіл бөлді. Атап айтқанда, ол 1871 жылы жарық көрген және автордың көзі тірісінде бірнеше рет қайта басылған "жылу теориясы" (жылу теориясы) оқулығын аяқ- тады. Бұл кітаптың көп бөлігі жылу құбылыстарын феномено- логиялық тұрғыдан қарастыруға арналған. Осы кітаптың 7-тарауында Максвелл Карноның қарапайым циклін қарастырды және геометриялық себептермен оның термодинамикалық диаграммадағы ауданын есептей отырып, Максвелл қатынасы деп аталатын термодинамикалық шамалар арасындағы төрт қатынасты алды.

Өмірінің соңғы жылдарында Максвелл Дж. Уиллард Гиббс және "жылу теориясының" қайта басылымдарын дайындауда оның әдістерін қабылдады, сонымен қатар оларды мақалалар мен баяндамаларда кеңінен насихаттады. Олардың негізінде ол кітапта қолданған энтропияның анықтамасын нақтылады [6], Бұл ұғым Максвеллдің қатынастарын алғаш жариялаған кезде оларды тұжырымдауда да қолданылмады.

Максвеллдің арақатынасын шығару

Максвеллдің арақатынасы термодинамикалық потенциалдардың аралас туындыларының теңдігінен алынады. Кез келген термодинамикалық потенциал үшін f тәуелсіз айнымалылар функциясы ретінде қарастырылатын x және y әділ қатынасы:

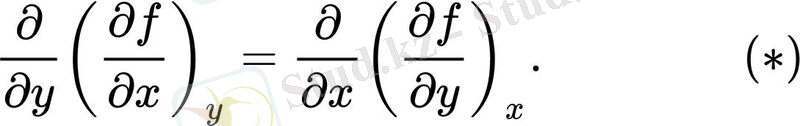
Термодинамикада әдеттегідей ішінара туындылардың төменгі оң жағында туындыны есептеу кезінде тұрақты деп саналатын айнымалылар көрсетілген. Бұл белгіні енгізудің себебі-термодинамикада бір функция үшін тәуелсіз айнымалылардың әртүрлі жиынтығы қолданылады, олар белгісіздікке жол бермеу үшін тізімделуі керек.

Термодинамикалық потенциалдың мысалы ретінде ішкі энергияны келтіруге болады U. Оның дифференциалына өрнек жазайық[7] : dU=TdS−PdV, қайда T - термодинамикалық температура, S - энтропия, P - қысым және V - көлем. Өрнек тәуелсіз айнымалыларға қатысты толық дифференциал болып табылады S, V:

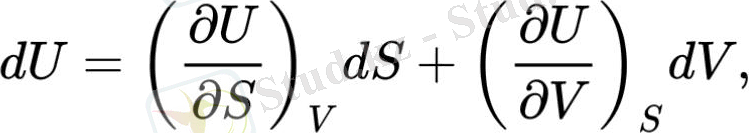
ішкі энергия туындыларын алуға не мүмкіндік береді:

(*) Теңдеуінен f=U, x=S, y=V:

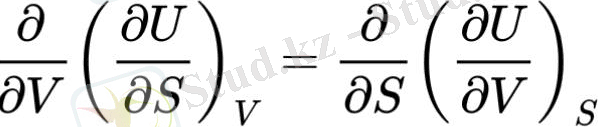
ішкі энергияның аралас туындылары үшін Максвеллдің бірінші қатынасы жүреді:

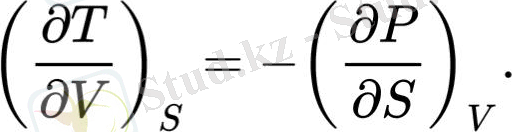
Кері функцияның туындысы үшін өрнекті қолдану,

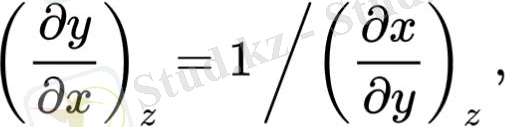
Максвеллдің бірінші қатынасы келесі түрге әкелуі мүмкін:

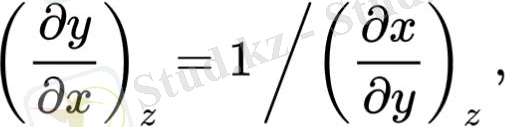
Келесі өрнектен:

dF=−SdT−PdV Гельмгольцтің бос энергия дифференциалы үшін F=U−T S оның бірінші ретті туындыларына арналған өрнектер:

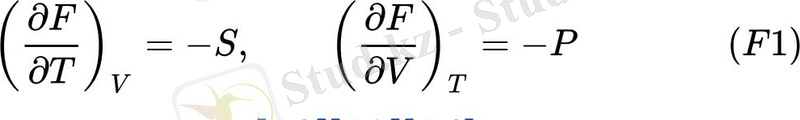
Максвелл кітабында жоқ болса да, тағы екі қатынас, Қазіргі әдебиетте Максвелл қатынасы деп аталуы мүмкін:

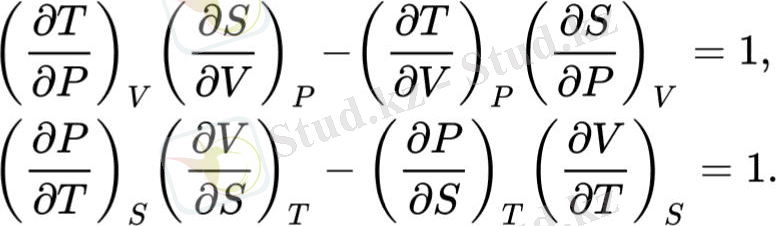
Негізгі мақала: якобиан әдісі (термодинамика) Термодинамикалық формулаларды, соның ішінде Максвеллдің арақатынасын қысқаша және талғампаз жазу үшін якобиандар қолданылады. Максвеллдің якобиандар арқылы көрсетілген алғашқы қатынасы осылай көрінеді[23] :

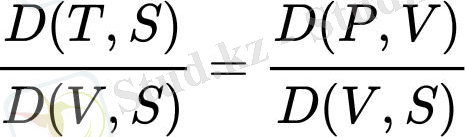
Егер (J) теңдеуінің екі бөлігін де көбейтсек D(V, S) /D(P, V) және якобиялық түрлендіру ережелерін қолданыңыз, сәйкестік алынады:

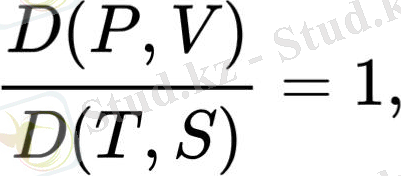
бұл Максвеллдің қатынасы.

Максвелл коэффициенттерін қолдану мысалдары

Максвелл коэффициенттерін қолдана отырып, кез-келген күйдің энтропиясын эксперименттік мәліметтерден интеграциялау арқылы есептеуге болатын іс жүзінде маңызды теңдеулер шығарылады[24] . Олар тәуелсіз айнымалылардың функциясы ретінде энтропияның толық дифференциалына арналған өрнектерден алынады T, V немесе T, P:

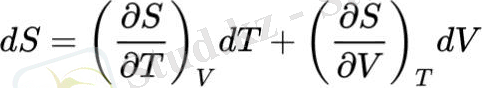
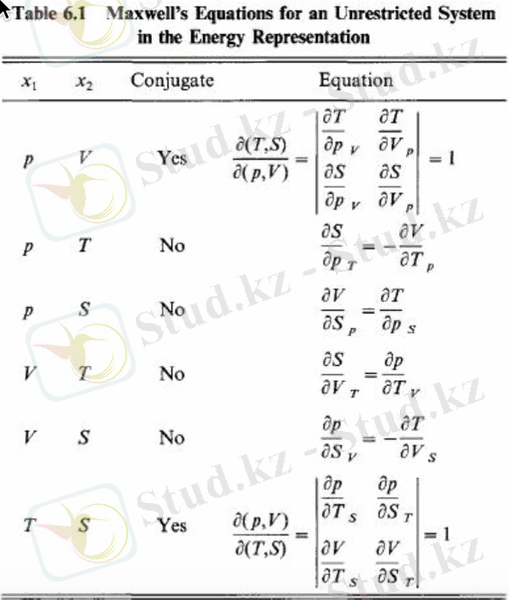
Энтропияның температуралық туындысы тұрақты көлемде (өлшенетін) жылу сыйымдылығы арқылы көрсетіледі CV≡(∂U∂T) V=T(∂S∂T) V немесе тұрақты қысыммен CP≡(∂H∂T) P=T(∂S∂T) P. Көлемі бойынша энтропия туындысы Максвеллдің екінші қатынасымен (F2), ал қысым туындысы Максвеллдің төртінші қатынасымен (G2) өрнектеледі, бұл энтропияны анықтау үшін қажетті теңдеулерді береді:

Тұрақты көлемдегі идеалды газ үшін қысым температураға пропорционалды (Чарльз заңы), сондықтан (∂P/∂T) V=P/T және алынған өрнек (∂U/∂V) T нөлге айналады. Осыдан Джоуль Заңы шығады - газдың ішкі энергиясының көлемнен тәуелсіздігі, сондай-ақ жылу сыйымдылығы арасындағы байланыс CV және CP:

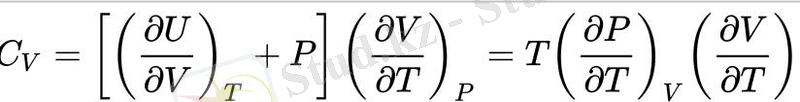
Сол сияқты, T, P айнымалыларындағы энтальпия дифференциалының өрнегін алуға болады:

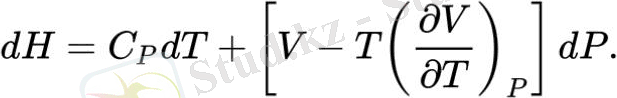
Демек, энтальпия сақталған кезде өтетін Джоуль - Томсон процесінде температура мен қысым дифференциалдарын байланыстыратын Джоуль-Томсон коэффициентінің өрнегі (dH=0) .

Максвеллдің күрделі термодинамикалық жүйелерге қатынасы

Неғұрлым күрделі термодинамикалық жүйелердің күйі екіден көп параметрлермен сипатталады, ал соңғыларының санының өсуімен термодинамикалық потенциалдың аралас туындыларының теңдігінен шығаруға болатын термодинамикалық сәйкестіктер саны да артады. Мысалы, бөлшектердің айнымалы саны бар ашық бір компонентті жүйе үшін N Гиббс энергиясының дифференциалына арналған өрнектен

Кейбір авторлар[32] [33] [34] термодинамикалық туындылар үшін кез-келген сәйкестікті "Максвелл қатынастары" деп атайды, оларды кейбір айнымалылар жұбы бойынша белгілі бір потенциалдың аралас туындыларының теңдігі ретінде жазуға болады. Мұндай қатынастар күрделі жүйелер үшін маңызды[29], онда термодинамикалық жұмыс[35], қысу/кеңейту жұмысынан басқа −PdV, басқа жұмыс түрлері кіреді. Мұндай жүйелер үшін термодинамиканың алғашқы басталуы, демек, ішкі энергия дифференциалының көрінісі термодинамикалық жұмыстың [29] түріндегі үлесін қамтиды:

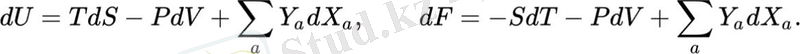
қайда Xa - жалпыланған термодинамикалық координаттар (көлемге ұқсас), а Ya - жалпыланған термодинамикалық күштер, а индексі күш - координат жұптарын нөмірлейді. осы түрдегі тағы алты өрнекті өрнектерден алуға болады dH, dG, және барлық төрт түр потенциалы үшін U−∑aXaYa, координаталық дифференциалдардың орнына дифференциалы dX a күш дифференциалдары арқылы өрнектеледі . Бензолдың беттік керілуі температурамен төмендейді Фазалар бөлімінің бетінің ауданын таңдағанда X1=Ξжалпыланған термодинамикалық координат ретінде жалпыланған күш беттік керілу болып табыладыY1=σ[және берілген қатынастардың екіншісі] :

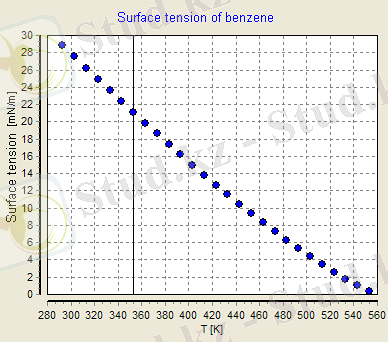
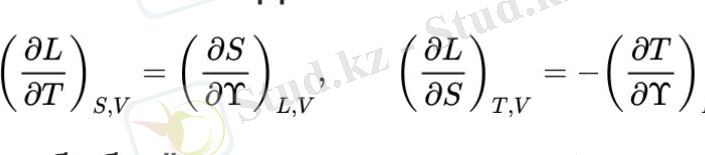
Мұнда шамасы r=T(S2−S1) /(Ξ2−Ξ1) энергияның қатынасына тең T(S2−S1) бетінің изотермиялық өсуімен сіңеді Ξ1дейін Ξ2, ауданның өзгеруіне Ξ2−Ξ1. Әдетте r >0, сондықтан беттік керілудің температуралық туындысы теріс болады және ол температурамен төмендейді. Бензол үшін мұндай температураға тәуелділіктің мысалы суретте келтірілген.

Пікірлер

Алғашқы басылымдарда қатынастарға кіретін шама Φ"термодинамикалық функция" деп аталды және оның анықтамасы "энтропия"ұғымынан өзгеше болды. Кейінгі басылымдарда бұл туралы айтылады Φ - термодинамикалық функция немесе (бірдей) энтропия.

Ландау мен Лифшиц бұл қатынасты басқа жолмен алды. Беттік керілу тек температураға байланысты, сондықтан бетті кеңейту жұмысының дифференциалы Y1dx1=σdΞ изотермиялық процесс үшін біріктіріліп, беттік бос энергияны алуға болады Fs=σΞ, содан кейін энтропияның беткі бөлігі Ss=−(∂Fs∂T) Ξ=−dσdTΞжәне беттік энергия Us=Fs+TSs=(σ− TdσdT) Ξ. Бетінің изотермиялық өсуі кезінде сіңірілетін жылу мөлшері Ξ1 дейін Ξ2, тең Q=T(S2−S1) =−TdσdT(Ξ2−Ξ 1), сонымен термодинамиканың алғашқы басталуына сәйкес беттік энергияның өзгеруі жылу қосындысына тең Q және жұмыс σ(Ξ2−Ξ1) . Белгілеуді енгізуr =Q/(Ξ2−Ξ1) =−TdσdT Максвелл коэффициентімен алынған теңдеуді береді.

Қолданылған әдебиеттер:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.