Математикалық статистика элементтерімен танысу

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Математикалық статистика элементтерімен танысу

Жоспар

Статистикалық жиынтық
Бас жиын үлестіруінің белгісіз параметрлерін нүктелік бағалау
Қисындылық баға
Ығыспаған баға

Кіріспе

Тәжірибеден алынған мәліметтер бойынша кездейсоқ шамаларды үлестіруін және оның параметрлерін анықтайтын математикалық аппарат қажет. Математикалық статистика әдістерінің мақсаты статистикалық мәліметтерді жинастыру, оларды өңдеу, белгісіз бас жиынтық үлестіруінің параметрлерін және белгісіз үлестіру функцияларын бағалау, сондай-ақ параметрлер мен үлестірулер жайындағы статистикалық гипотезалардың дұрыстығын тексеру болмақ. Статистикалық әдістер белгінің сандық түрінде ғана қолданылады. Ал белгі мәні болса санмен өлшенуі де мүмкін, сапалық болуы да мүмкін.

Қандай болса да біз оларды сандық түрге келтіруіміз қажет, сонда ғана статистикалық әдістерді пайдалана аламыз.

Ал барлық белгілерді бірден қарастыру мүмкін емес. Сондықтан зерттеуші олардың ішіндегі біреуіне көңіл аударады да, қалған белгілер үшін жиындағы обьектілерді тең құқылы деп ұйғарады, сөйтіп мұндай обьектілер жиынын біртекті дейтін болады. Осындай тәсілмен жасалған біртекті жиынды статистикалық жиынтық деп атайды, ал оны құраушы обьектілерді жиынтық бірліктері дейді.

Обьектілер сандық қасиет сияқты сапалық қасиетке де ие болады. Мысалы сандық қасиетке баланың бойының өсуін жатқызуға болады.

Статистикалық жиынтық сандық немесе сапалық белгіге ие болатын барлық біртекті обьектілерді біріктірсе, ондай жиынтық бас жиынтық деп атайды.

Егер бас жиын шексіз немесе өте көп болса, ондай зерттеу үшін алынған оның бөлігін таңдама жиынтық дейді.

Ықтималдық теориялық моделдер Гаус заңы, Пуассон заңы тағы басқа белгілі, сандық параметрлермен сипатталатыны мәлім.

Мысалы қалыпты заң үшін мұндай параметрлер математикалық күтім µ және орташа ауытқу δ болса, Пуассон заңы үшін ондай параметр λ болады. Бас жиын параметрін θ десек, ал таңдама параметрін θ² десек, онда θ²-ны θ-нің бағасы ретінде қарастырады. θ² қаншалықты θ-ға жуық екенін білуді айқындау үшін математикалық аппаратты қолдану керек.

Бас жиын үлестіруінің белгісіз параметрлерін нүктелік бағалау.

Үлестірудің әрбір параметрі шекті материал көлемінде есептелгендіктен әр уақытта кездейсоқтық элементі болады. Сондықтан бұл мәнді зерттеп отырған бас жиынды сипаттайтын параметр мәнімен тепе-тең деп қарастыруға болмайды. Демек, θ-ні тек θ² мәнінің бағасы деп қарастыру керек. Ал θ-ны бір ғана санмен бағалағандықтан, мұндай бағалауды нүктелік бағалау деп атайды.

Ал нүктелік баға Х кездейсоқ шама болғандықтан θ-ға қатысты әр түрлі ауытқулар беруі мүмкін. Сондықтан, зерттелген таңдамалардың

θ²α, . . . θ²µ параметрлерінің ішінен θ-ға қатысты ең аз ауытқу беретін және θ-ны жақсы бағалайтын θ²-ті таңдап алатын критерийді табу керек. Ол үшін Швед статистигі Г. Крамер айтуы бойынша төмендегі үш жұмыс орындалуға тиісті.

Θ-ға ең жуық мән беретін θ² бағасына қойылатын талаптарды анықтау
Бағаларды табу әдістерін анықтау
Бас жиын параметрлері туралы сенімді қорытынды алу үшін бұл бағаларды пайдалану мүмкіндіктерін көрсету.

Қисындылық баға

Әрине θ²-ның әрбір θ²1, θ²2 . . . мәні θ² параметрімен дәл бірдей болатын θ² бағасы табылса, ол іздеген θ²-ның анық бағасы болатынына күмән жоқ. Алайда машықтануда мұндай жағдайдың болуы қиын. Бірақ θ²=θ жағдайына таңдама көлемі N мейлінше үлкен болғанда θ²1, θ²2 . . . мәндерін біртіндеп орталандыра отырып θ²-ға үлкен сандар заңында көрсетілген жолмен жуықтауға болады.

Бұл жағдайда

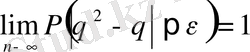
Болады, яғни θ² ықтималдығы бойынша θ-ға жинақталады. /мұнда е-қандай да аз оң таңбалы сан/

Сонымен, бас жиынның белгісіз θ² параметрінің бағасы үлкен сандар заңына бағынатын болса, онда қисындылық талабын қанағаттандырады делінген.

Ығыспаған баға

Шаманың математикалық күтімі бас жиын параметрі θ²-ға тең болатын бағаны ығыспаған баға дейді, яғни М(θ²) = θ

Бағаның ығыспағандығы жүйелік қатенің болмауын және θ²1, θ²2 . . . параметрінің центр деп аталатын θ параметрлерінің ауытқуларының абсолютті шамалары бірдей болуын талап етеді.

Тиімді баға

θ параметрін бағалаудың тиімділігі дегенде, θ параметрінің бірнеше бағасының ішінен ең тиімдісін алу болып табылады.

Қолданылған әдебиеттер