Виет теоремалары

Жоспар
Кіріспе

Жоспар

І. Кіріспе:
1 Қайта өрлеу заманындағы ғылымның жағдайы

ІІ. Негізгі бөлім:
1 Франсуа Виеттің өмірбаяны
2 Виет теоремасы
3 Виет теоремасына байланысты есептер шығару

ІІІ. Қорытынды

Қайта өрлеу заманы математикасының ең биік шоқтығы, яғни әлемдік мате-
матикаға үлесін қосқаны – Франсуа Виеттің математикалық еңбектері. Оның
есімімімен орта мектеп математикасындағы ең бір тамаша теореманың атау-
лында үлкен мән бар.
Франсуа Виет (1540-1603) Францияның Пуату провинциясында дүниеге кел
ген. Ол оқыған мамандығы бойынша заң қызметкері. Ұзақ жылдар бойы ол
өзінің туған қаласында адвокаттық жұмыспен айналысқан. Алайда Виеттің
негізгі мақсаты математик болу еді. Ол астрономиядан сабақ бере жүріп,
тригонометрия мәселелерін зерттейді, талдайды. 1570 жылы "Математика-
лық канон" деп аталатын трактаты жарық көреді.
Виет математикасының ең негізгі жетістігі алгебра саласын ашуы. Ол шын
мағынасында жаңа символикалық алгебраның негізін жасады, яғни санды
әріппен белгілеген ғалымдардың алғашқыларының бірі болды.
Жаңа алгебраның жалпы идеялары мен негізгі принциптерін Виет "Аналити
калық өнерге кіріспе " еңбегінде баяндайды. Мұндағы оның мақсаты- көне
алгебраны қуатты математикалық есептеу құралына айналдыру.
Виет жалпы алгебраны екі бөлікке ажыратады: біріншісі –жалпы шамалар-
ды (скалярды) қарастырады. Екіншісі біріншісіне сүйене отырып, сандарды
қарастарыды. Жалпы алгебраны ол түрлік логистика (logistica species),ал екнішісін–сандық логистика (logistica numeralis) деп атайды.Алгебраның
бұл екі бөлігі арасында тығыз байланыс бар, олардың заңдылықтары бір-бірі
не тікелей сәйкес келеді. Мәселен, сандарды көбейтуге өлшемдері берілген
шамалардың өлшемдерінің қосындысына тең болатындай жаңа шама табу
сай келеді.(Мектеп математикасының тарихи мағлұматтары, Алматы
2004ж, Ә.Бидосов, 51-52 беттер) Осындай сәйкестік арқасында түрлік логис
тика нәтижелерін (заңдылықтарын) геометрия есептеріне де, сандық логисти
каға да бірдей қолдану мүмкін болады. Алайда бұл екі алгебра бір-бірімен
теңбе-тең деп айтуға келмейді, өйткені шамалар (скалярлар) жүйесі сандар
өрісінің де, сақинасының да қасиетіне ие болмайды.
Виет өзінің алгебрасында тек белгісіздер үшін ғана емес кез келген, яғни ай-
нымалы шамалар үшін де таңбалар енгізеді. Мұны ол бас әріптерімен: дауыс
тылармен белгісіздерді, дауысыыздармен белгілі шамаларды белгілейді. Бұл
әріп коэффиценттерін қолданудағы жаңалық алгебраның дамуындағы негізгі
бетбұрысқа бастама болды, осыдан кейін барып алгебралық есептеулер, фор-
мулалар жүйесі оперативтік алгоритм түріне көшті. "Коэффицент" деген
сөздің өзін математикаға бірінші енгізген осы Виет еді. Мысалы, ол (А+В)2+
+D(А+В) түріндегі өрнекті қарастыра келіп, А+В мен қосылып D(А+В) тік-
төртбұрышын құрайтын D шамасын longitudo coefficiens, яғни көмектес ұзын
дық деп атайды.

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 12 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ
БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
АБАЙ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ
ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
ФИЗИКА-МАТЕМАТИКА
ФАКУЛЬТЕТІ
МОК-092ГР

ТАҚЫРЫБЫ: ВИЕТ ТЕОРЕМАЛАРЫ

ОРЫНДАҒАН: 1-КУРС СТУДЕНТІ

ЕСЕНҒАЛИЕВ С.Т.

ТЕКСЕРГЕН: П.Ғ.К.,АҒА ОҚЫТУШЫ

ДЖАНАБЕРДИЕВА С.А.

АЛМАТЫ-2009Ж

Жоспар

І. Кіріспе:
1 Қайта өрлеу заманындағы ғылымның жағдайы
ІІ. Негізгі бөлім:
1 Франсуа Виеттің өмірбаяны
2 Виет теоремасы
3 Виет теоремасына байланысты есептер шығару
ІІІ. Қорытынды

Cабақтың тақырыбы: Виет теоремалары

Сабақтың мақсаты: Квадрат теңдеулерді қарапайым жүйеге
келтіріп, Виет теоремасын қолдану. Оқушыларды алгебраға
деген қызығушылықты таныту.

Франсуа Виет
(1540-1603)
Қайта өрлеу заманы математикасының ең биік шоқтығы, яғни әлемдік мате-
матикаға үлесін қосқаны – Франсуа Виеттің математикалық еңбектері. Оның
есімімімен орта мектеп математикасындағы ең бір тамаша теореманың атау-
лында үлкен мән бар.
Франсуа Виет (1540-1603) Францияның Пуату провинциясында дүниеге кел
ген. Ол оқыған мамандығы бойынша заң қызметкері. Ұзақ жылдар бойы ол
өзінің туған қаласында адвокаттық жұмыспен айналысқан. Алайда Виеттің
негізгі мақсаты математик болу еді. Ол астрономиядан сабақ бере жүріп,
тригонометрия мәселелерін зерттейді, талдайды. 1570 жылы "Математика-
лық канон" деп аталатын трактаты жарық көреді.
Виет математикасының ең негізгі жетістігі алгебра саласын ашуы. Ол шын
мағынасында жаңа символикалық алгебраның негізін жасады, яғни санды
әріппен белгілеген ғалымдардың алғашқыларының бірі болды.
Жаңа алгебраның жалпы идеялары мен негізгі принциптерін Виет "Аналити
калық өнерге кіріспе " еңбегінде баяндайды. Мұндағы оның мақсаты- көне
алгебраны қуатты математикалық есептеу құралына айналдыру.
Виет жалпы алгебраны екі бөлікке ажыратады: біріншісі –жалпы шамалар-
ды (скалярды) қарастырады. Екіншісі біріншісіне сүйене отырып, сандарды
қарастарыды. Жалпы алгебраны ол түрлік логистика (logistica species),ал
екнішісін–сандық логистика (logistica numeralis) деп атайды.Алгебраның
бұл екі бөлігі арасында тығыз байланыс бар, олардың заңдылықтары бір-бірі
не тікелей сәйкес келеді. Мәселен, сандарды көбейтуге өлшемдері берілген
шамалардың өлшемдерінің қосындысына тең болатындай жаңа шама табу
сай келеді.(Мектеп математикасының тарихи мағлұматтары, Алматы
2004ж, Ә.Бидосов, 51-52 беттер) Осындай сәйкестік арқасында түрлік логис
тика нәтижелерін (заңдылықтарын) геометрия есептеріне де, сандық логисти
каға да бірдей қолдану мүмкін болады. Алайда бұл екі алгебра бір-бірімен
теңбе-тең деп айтуға келмейді, өйткені шамалар (скалярлар) жүйесі сандар
өрісінің де, сақинасының да қасиетіне ие болмайды.
Виет өзінің алгебрасында тек белгісіздер үшін ғана емес кез келген, яғни
ай-
нымалы шамалар үшін де таңбалар енгізеді. Мұны ол бас әріптерімен: дауыс
тылармен белгісіздерді, дауысыыздармен белгілі шамаларды белгілейді. Бұл
әріп коэффиценттерін қолданудағы жаңалық алгебраның дамуындағы негізгі
бетбұрысқа бастама болды, осыдан кейін барып алгебралық есептеулер, фор-
мулалар жүйесі оперативтік алгоритм түріне көшті. "Коэффицент" деген
сөздің өзін математикаға бірінші енгізген осы Виет еді. Мысалы, ол (А+В)2+
+D(А+В) түріндегі өрнекті қарастыра келіп, А+В мен қосылып D(А+В) тік-
төртбұрышын құрайтын D шамасын longitudo coefficiens, яғни көмектес ұзын
дық деп атайды.
Виеттің символикасында "+" және "–" таңбалары кездеседі, көбейтінді іn де-
ген сөзбен беріледі. Дәрежені көрсету үшін тиісті әріпке quadratum, cubus
т.б.
сөздерді тіркестіреді. Мысалы біздің жазуымыздағы х2 –3r2х =r3 түрде жазы-
лады: А cubus + Z quadrato terin A aequator Zcubo. Мұндағы ter сөзі –үш
есе,

aequator –тең дегенді білдіреді. Мұнда теңдеудің мүшелерінің барлығының
бірдей өлшемді болып келетіні байқалады, яғни Виеттің алгебрасында әлі де
болса ежелден келе жатқан геометрия ықпалы күшті. Айрықша гоеметриялық
терминология енгізіледі: шаманың бірінші дәрежесі latis (қабырға), екіншісі
–planum (аудан), үшіншісі –solidum(дене) т.с.с. Қосу және азайту тек бірдей
өлшемді шамалар үшін қолданылады. Бұл талап орындалу үшін, яғни өлшем-
ді шамалар үшін қолданылады. Бұл талап орындалу үшін, яғни өлшемді те-
ңестіру үшін ұзындықтың бірлік өлшеміне көбейтуге рұқсат етіледі. Көбейту,
бөлу өлшемділікті өзгертеді. Виеттің бұл идеялары сандар мен шамалар ара-
сында математикалық 2000 жыл бойы қалыптасқан айырмашылықтың жікте-
луінің көрінісі болады. Сондықтан да Виеттің символикасында геометриялық
таңбаулар мен қосымшалар көп кездеседі.Мысалы: А cubus + В planumіn A3
aequator D solido ( A3+3BA=D). Қалай болғанда да Виеттің символикасы тең-
деулерді, олардың қасиеттерін жалпы формула арқылы өрнектеуге мүмкіндік
беретін ең тұңғыш кемел символика еді. Осының арқасында математикалық
операциялардың объектісі сандық есептер емес, таза алгебралық өрнектер
болды. Виет өзінің есептеулеріне баға бере келіп, оны "математикалық
жаңалықтар ашуды жасыратын өнер" деуі тегін емес. Виеттің таңбаулары
көп ұзамай оның шәкірттерінің еңбектерінде,әсіресе Гэрриоттың (1560-1621)
еңбектерінде одан сайын жетілдіре түсті.
Өзінің символикалық есесптеуін Виет алгебра мәселелерінің көп салаларын
зерттеп шешуге қолданады. Бұл тұрғыда ең әуелі оның бірінші –төртінші дә-
режелі теңдеулер теориясын толық аналитикалық баяндауын айту керек.Бұл
ретте Виеттің екі нәтижесін келтірумен шектелейік. "Теңдеулерді кемелден-
діру" атты шығармасында ол х3+3ах=2в түріндегі куб теңдеуін у2+ху=а түр-
лендіруі арқылы у3 бойынша квадрат теңдеу болатын у6+2ву3=а3 теңдеуіне
келтіреді. Екіншісі "Геометрияға қосымша" деп аталатын еңбегінде куб
теңдеудің келтірілмейтін жағдайын бұрышты трисекциялау есебіне келтіреді.
Егер х3-рх=q теңдеуін х3 – 3r2х =аr2 (р=3r2 және q=аr2) түрінде жазсақ,
онда
r 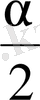болған жағдайда теңдеу келтірілмейтін түрге келеді. cos3α=4cos3α-

-3cosα теңбе-теңдігімен салыстыра отырып, а=2r cos3α деп алуға болады.
Сонда теңдеудің шешуі х=2r cosα болады деп есеп берілген cos3α бойынша
теңдеуін шешеді: х=2cos20, бұдан cos200=0,93969262. Теңдеулерді шешуде
Виет оның оң түбірлерін іздестірді. х= –у түрлендіру арқылы ол теріс түбір-
лер мәселесін де қояды. Карданоның зерттеулерін дамыта келіп, Виет теңдеу-
лер түбірлері мен оның коэффиценттері арасындағы өзара байланыс туралы
бірсыпыра қорытындылар жасайды. Мұның ішінде қазір оның атымен ата-
лып жүрген Виет теоремасының дербес жағдайлары да бар.
Виет өзінің алгебралық жетістіктерін математиканың тригонометрия сияқты
басқа салаларына қолдануға көп көңіл бөледі.Ол алгебралық әдісті қолданып,
берілген үш элемент бойынша жазық және сфералық үшбұрыштың барлық
элементін табады.
Виет екі бұрыштың қосындысының синусы мен косинусының формулаларын
қайталап қолданып, еселі доғалардың (бұрыштардың), тригонометриялық
функциялардың жіктелу әдісін табады:

sin m α=cosm-1 α sin α 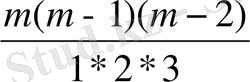cosm-3α sin3α+...

cos m α=cosm α 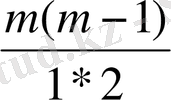cosm-2α sin2α+...

Виет көптеген тригонометриялық реккуренттік (қайталама) формулаларлы
білген. Мысалы,

cos m α = 2 cos α cos (m-1) α – cos (m-2) α
sin m α = 2 cos α sin (m-1) α – sin (m-2) α
sin m α = 2 sin α cos (m-1) α + sin (m-2) α
cos m α = – 2 cos α cos (m-1) α +cos (m-2) α

Виет еңбектерінде алгебралық және тригонометриялық зерттеулердің бір-
бірін толықтырып отыратын жағдайы жиі кездеседі. Бұл тұрғыда мынадай бір
мысал келтірейік. 1594 жылы голландиялық математик Адриан ван Роумен (1561-
1615) бүкіл дүние жүзі оқымыстыларына сандық коэффицентті
45 ші дәрежелі мынадай есепті шешуді ұсынады:

45х – 3795х3 + 95634х3 – 12300х39 + 945х41 – 45х49 + х43=а
Мұндағы а=

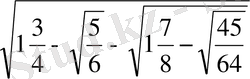
Виет мұның бір шешуін тригонометриялық жолмен бірден табады: а радиусы
1-ге тең дөңгелекке іштей сызылған 15-бұрышты көпбұрыштың қабырғасы,
яғни 240 доғаның хордасы екенін біледі, сонан соң бірінші және ең соңғы
мүшенің алдындағы мүше коэффиценттері (45) бойынша х-тің осы доғаның
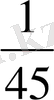бөлігі екенін анықтайды. 2sin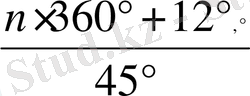(n=1, 2, ..., 22) формуласы
арқылытағы да 22 түбір табады. Қалған 22 теріс түбірді ол есепке алмайды.
Жалпыол скаляр шамаларға сәйкес келмейтін теріс, жорымал сандарды кәдімгі
сан қатарына қоспаған.
Трансцендентті функцияларды алгебралық теңдеулерді шешуге қолдану
Виеттен кейін ХІХ ғасырдың екінші жартысынан бастап қана қана дамыды
(Ш.Эрмит, Л.Кронокер және т.б.).
Виеттің математика тарихындағы тағы бір үлкен жетістігі – оның алғашқы
рет шексіз көбейтінділерді қарастыруы. Ол мұндай көбейтіндіні π санын таза
аналитикалық түрде кескіндеуге, өрнектеуге пайдаланған. Бұл жаңалықты ол
"Математикалық әр түрлі сұрақтарға жауап кітабында" келтіреді.
Радиусы 1-ге тең дөңгелекке ауданы Sn болатын дұрыс бұрыш іштей сызыл-
ған делік. Бұл n-бұрышқа іштей сызылған дөңгелектің радиусын r деп белгі-
лейік.
Сонда: Sn : S2 n= rzn: r = cos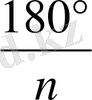, n = 4 болғанда, Sn = 2r2 . Егер бір-
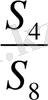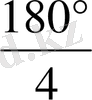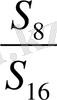бірлеп n = 4, 8,16,20... деп алып және мұнда шығатын = соs ,
= соs 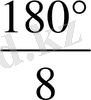т.с.с. теңдіктерді өзара көбейтсек және n →∞ болғанда
S2n -нің шегі дөңгелек
тің ауданы болатынын ескерсек, мынадай шексіз көбейтінді шығады:

=

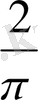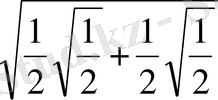
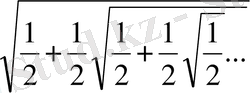
Виет бұл шексіз көбейтіндінің жинақы болатынын қарастырмайды. Өйткені
іштей сызылған дұрыс көпбұрыштарды екі еселей бергенде оның шегі дөң-
гелек болатынына ол ешбір күмән келтірмеген.
(Математика тарихы,Алматы 1993,Көбесов А,158-163беттер)

Виет теоремасы

Математикалық өлең сөйлемдер. Теоремаларды, аксиома, анықтамаларды,
ережелерді өлеңмен беру оқушылардың пәнге деген қызығушылығын туды-
рып, қызықты сипат береді.
Виет теоремасы
Виеттің лайықты екен, әнге қосу,
Теорема –түбірлер қасиеті.
Көбейтсек түбірлерді –бөлшек дайын,
Алымы – с ,ал бөлімі а болатын .
Ал түбірлер қосындысы тағы бөлшек:
Болса да минусымен таңбасы ерек,
Тағы да бөлшек дайын болып шықты–
Алымы b болса да, бөлімі а.
(Қызықты математика,Алматы 2009, Джанабердиева С.А, 20-21беттер)

Виет теоремасы. Біз х2 + рх + q = 0 квадрат теңдеу екенін
білеміз.Мысалы,
х2 + 7х + 12 = 0 -квадрат теңдеу. Мұнда D = 49 – 4 12 = 1 болса, онда осы
теңдеудің жауаптары(түбірлері) х1 = 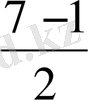= 3 ; х2 = 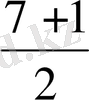= 4.
Осыдан
3 + 4 = 7 = – (– 7) және 3 4 = 12 екенін байқау қиын емес. Осыдан орай,
квад-
рат теңдеудің түбірлері мен коэффиценттердің арасында тығыз байланыс
болады. Ендеше, Виет теоремасын дәлелдеп, сонда ол жалпы түрде байланы-
сын көрсетеді.
Теорема 1. Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-
қарсы таңбамен алынған оның екінші коэффицентіне тең, ал түбірлерінің
көбейтіндісі бос мүшесіне тең:

х1 + х2 = – р
х1 х2 = q
Дәлелдеуі. х2 + рх + q = 0 теңдеуінің шешімдері х1 = ;
х2 = өзара теңдіктерімен анықталады. Онда
х1 + х2 = + = = – р
х1 . х2 = . = = = q
Теорема дәлелденді.
Жалпы түрде ах2 + bх + с = 0 теңдеу = 0 келтірілген квадрат тең-
деумен бірдей. Виет теоремасы бойынша х1 + х2 = х1 . х2 =
Мұндағы:
ах2 + bх + с = 0; х1 , х2 – квадрат теңдеудің түбірлері.

Кері теорема. Виет теоремасына кері тұжырымда орындалады.

Теорема 2(Кері теорема). Егер и + v = – р, и v= q болса, онда и және v
сандары х2 + рх + q = 0 теңдеуінің түбірлері болады.

Дәлелдеуі. Айталық, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.