Кванттық химиялық зерттеу әдістері: жартылай эмпирикалық, ab initio, тығыздық функционал теориясы және базистік жиындардың салыстырмалы талдауы


- Кванттық химиялық зерттеу әдістері
2. 1 Квантты химия әдістерінің жалпы сипаттамасы
Практикада әдетте жартылай эмпирикалық және эмпирикалық емес әдістер қолданылады. Олар кванттық химияның негізгі теңдеулеріндегі электрондардың өзара және электрондар мен атомдық ядролардың әрекеттесуін сипаттайтын матрицалық элементтерді анықтау әдісімен ерекшеленеді. Осы мақсат үшін жартылай эмпирикалық әдістерде жуықталған эмпирикалық формулалар және эксперименттен белгілі атомдық параметрлер қолданылады. Эмпирикалық емес әдісте матрицалық элементтердің тікелей аналитикалық есептеулері жүргізіледі. Маман емес адамдарға «эмпирикалық емес» атауына синоним «тура» сөзі болып табылады, бірақ шынында олай емес. Эмпирикалық емес әдіс те жуықталған болып табылады, пайдаланылған базистің толық еместігіне байланысты. Көптеген эмпирикалық емес есептеулерді үлкен емес және орташа базисте жүргізеді. Бұл есептің нәтижесіне айтарлықтай қателік туғызады, өйткені мұндай базистік жиындар молекуладағы электрондық тығыздықтың таралуының кейбір ерекшеліктерін бере алмайды. Нәтижесінде барлық молекулалардың параметрлері аздаған қателікпен анықталады. Мүмкіндігінше (уақыттың көп кетуінен мұны практикада жасау өте қиын) өте үлкен базистарды қолдануға болар еді, олар ХФ-ның шектеуіне жетуге қамтамасыз етеді, онда базистік орбитальдің өсу саны алынған нәтижелеріне жетпейді. Бұндай жағдайда да Шредингер теңдеуінің нақты шешімін таба алмаймыз. Шредингер теңдеуінің нақты шешімін табу үшін электрондық корреляцияны ескеру қажет.
Қазіргі химияның дамуындағы аса маңызды роль атқарған басқа бағыт ХФ әдісіндегі бір электрондық және екі электрондық интегралдық анықтауынан бас тарту болып табылады. Нақты Фок операторының орнына жуықталған операторы қолданылады, оның элементтерін эмпирикалық мәліметтерден алады. Тиісті параметрлерді әрбір атомдар және атомдар жұбы үшін таңдайды: осындай жағдайда олар тіркелген сан болып табылады немесе атомдардың өзара арақашықтығына тәуелді болады. МО есептелуі итерациялық жолымен жүргізіледі.
Жартылай эмпирикалық әдістер эмпирикалық емес әдістерге қарағанда бірнеше рет жылдам, олар үлкен жүйелерге (көбінесе өте үлкен жүйелерге, мысалы биологиялық) және кейбір қосылыстар кластары үшін дәлірек нәтиже береді. Бұл арнайы алынған кең емес қосылыстар класының параметрлері арқылы нәтижеге жетеді. Басқа кластарға көшкенде сол әдістер мүлдем дұрыс емес нәтижелер беруі мүмкін. Сонымен қатар есептеу параметрлері сол немесе басқа молекулалық қасиеттерді сипаттау үшін тандалады, сондықтан жеке параметрлерге физикалық мағына беруге болмайды.
Жоғарыда көрсетілген жуықтаулар толқындық функцияларды тек қана валенттік электрондар үшін минималды слейтерлік базис қолданып есептейді, ал ішкі қабаттардың электрондарын молекуланың қаңқасына қосады; электрондардың кулондық әрекеттесуінің матрицалық элементтің кейбір бөлігін ескермейді. Соңғы жорамал едәуір маңызды болып табылады, өйткені ол есептеуді едәуір қысқартуға мүмкіндік береді. Электронның кулондық әрекеттесуінде элементтің матрицалық саны өте үлкен болады, ол төртінші дәрежелі базистік орбиталь санына пропорционал, сондықтан базисті екі есе өсіргенде кулондық интегралды 16 есе көп есептеу қажет. Оларды есептеу өте көп мөлшерде уақыт алады және органикалық химия жағынан қызығушылық танытқан көптеген қосылыстар үшін қазіргі ЭЕМ практикалық тұрғыда іске аспайды.
Эмпирикалық емес әдісте электрондар мен атомдық ядролардың және электрондардың өзара әрекеттесуінің барлық матрицалық элементтері кейбір АО базисіндегі қажетті интегралдардың аналитикалық есептеу арқылы анықталады.
Қазіргі кезде органикалық қосылыстардың реакциялық қабілеттілігі мен құрылысын зерттеуде Попл ұсынған төмендегі базистер кең қолданылады: минималды базис ОСТ-3ГФ, валентті- ажыратылған базистер 3-21ГФ, 4-31ГФ, 6-31ГФ, поляризацияланған орбитальдары бар валентті-ажыратылған базистер 6-31ГФ* және 6-31ГФ**, диффузиялық s - және p - орбитальдары бар валентті-ажыратылған базисі 3-21+ГФ және 4-31+ГФ.
ОСТ-3ГФ-минималды базис, онда әрбір слейтерлік орбиталь үш гаусстық функцияның сызықтық комбинациясымен ауыстырылған.
3-21ГФ, 4-31ГФ, 6-31ГФ -валентті- ажыратылған базистер, онда әрбір слейтерлік орбиталь ішкі қабаттардағы электрондар үшін 3, 4, 6 гаусстық функциядан тұратын сызықтық комбинациямен ауыстырылады, ал валентті электрондар үшін әрбір слейтерлік орбиталь орнына гаусстық функциялардың екі сызықты комбинациясы қолданылады: біреуі екеуден (3-21ГФ базис) немесе үш (4-31ГФ және 6-31ГФ базис), ал екіншісі бір қарапайым гаусстық функциядан тұрады. Осы үш базиста топтасқан гаусстық функцияның саны бірдей болады, бірақ 6-31ГФ және 4-31ГФ базистерінде 3-21ГФ базисіне қарағанда қарапайым функциялардың саны көбірек.
6-31ГФ және 4-31ГФ базистерін қолдану электрондық тығыздықтың таралуының дәл аппроксимациясын алуға болады, әсіресе атомдық ядролардың жанында, бірақ молекулалардың көптеген физика-химиялық параметрлерін есептеген кезде нәтижелердің дәлдігі аса жоғарыламайды, ал уақыттың шығымы айтарлықтай көбейеді. Сондықтан қазіргі кезде қолданбалы жұмыстарда 3-21ГФ базисі кеңінен пайдаланылады.
6-31ГФ* және 6-31ГФ** - поляризацияланған d- орбиталі бар валентті-ажыратылған базистер. 6-31ГФ* базисіне р -элементтегі, яғни көміртегі, азот және т. б. атомдарындағы, поляризацияланған d- орбитальдары, ал 6-31ГФ** базисіне р -элементтеріндегі d- орбитальдары және сутегі атомдағы р-орбитальдар кіреді. Базиске поляризацияланған орбитальді қосу есептеудің дәлдігін әжептәуір көтереді, бірақ, өкінішке орай, бұл кезде уақыттың шығымы өте жоғары болады.
3-21+ГФ және 4-31+ГФ қосымша диффузиялық s- және р- орбитальдары бар аниондардың физика-химиялық параметрлерін кванттық-химиялық есептеуде қолданады. Электрнейтралды молекуладан анион түзілгенде МО диффузияланады. Бұл эффект зарядталмаған молекулаларды есептеу үшін таңдап алынған валентті-ажыратылған базис арқылы көрсетуге болмайды, сондықтан аниондар үшін осындай базисте эмпирикалық емес есептеулердің дәлдігі нейтралды қосылысқа қарағанда әжептәуір төмен болады. Дәлдіктің көтерілуі базиске қосымша диффузиялық s - және р -орбиталь қосу салдарынан болу мүмкін. Бұл аниондар үшін дәлдіктің көтерілуі эмпирикалық емес есептеудегі қадағалайтын экономикалық тәсілі. Бұл жағдайда уақыттың шығымы тек 1, 5 есе ғана өседі. Аниондарды оқығанда сонымен қатар поляризацияланған орбитальдары бар базистерді қолдануға болады, өйткені d- орбитальдары р- элементінде және р- орбитальдары сутегі атомында диффузиялық функция болып табылады, бірақ бұл жағдайда уақыттың шығымы есептеуде одан да көп өседі.
Квантты-химиялық әдіс негізінде істелген жуықталу талдауында оның қолдану облысын анықтау мүмкін емес және оларды оның көмегімен анықтауға болады. Өкінішке орай теориялық жағынан жақсы негізделген көптеген квантты-химиялық әдістер практикада нашар нәтижелер беретіндіктен қолданылмайды, ал сәтті алынған параметрлер көп қолданылады. Кейбір әдістерде жуықталу әкелетін қателіктер бір-бірінің орынын толтырады және нәтижесінде экспериментпен жақсы келісім шығады. Осындай компенсация болар-болмасын алдын-ала айтуға болмайды, сондықтан әрбір нақты әдістің қолдану облысын және нақтылығын сипаттауды бірнеше эксперименттің негізінде ғана анықтауға болады және материалдық есептеу жүйелігін жариялау керек.
Шредингердің молекулалық теңдеуінің ССП сұлбасы шегінде шешуінің оптималды жолдарын іздеу бастапқы кезден екі негізгі бағыт бойынша жүрген. Бірінші бағытта ол ab initio (эмпирикалық емес әдістер) болып табылады, оларды қазіргі уақытта да 10 атомнан асатын молекулалар және молекулалық фрагменттердің есептеулері үшін сирек қолданылады. Есептеу әдістерінің екінші тобы- жартылай эмпирикалық әдістер, органикалық және бейорганикалық химияның жаппай дамуына байланысты кең танымалдықты иеленіп келе жатыр. Дәл осы квантты химия әдістерінің пайда болуы мен мінсіздігі химик маманның жұмыс құралы болып, лабораториялық практикаға енуіне жол ашылды. Қол жеткізілген жетістіктермен қатар жартылай эмпирикалық әдістер нақты химиялық есептерді шешу кезінде нақты шешім болып табылмайды, олардың бірқатар кемшіліктері мен шектеулері бар. Осы топ әдістерінің дұрыс қолданылуы арқылы олардың мүмкіндіктерін, тапсырмалар ортасын химик-практик қарастырады, аталған әдістер осыларды шешуге негізделген [4] .
Дегенмен квантты химияның эмпирикалық емес (ab initio( лат. ) -«басынан») әдістері едәуір нақты және кезекті бола тұра, олардың кең қолданысын қиындататын принципиалды кемшіліктері жеткілікті:
-есептеу уақыты n4 сияқты өсуіне байланысты есептеулердің үлкен жұмыс сиымдылығы үшін кеңейтілген базисті қолдану кезінде N=10-20 атомдар санына сәйкес келетін енді n≈200-250 молекулалар үшін суперкомпьютерлер қолдану керек;
-кейде өлшемі жеткілікті берік ковалентті байланыстың энергиясымен теңесе алатын Е corr корреляциялық энергияның толық есепке алынуының мәселесі әлі күнге дейін шешілмеген. Осылай, мысалы, НF молекуласы үшін ССП есептеуі хартри-фоктық шектеуде 1 кестеде келтірілген сипаттамаларды береді [5] .
1 кесте
Эксперимент пен есептеулері бойынша НF молекуласының толық энергиясы (
1-кестедегі берілгендер бойынша көрініп тұрғандай, молекула энергиясының есептеуі кезінде болатын қатыстық қателік 0, 5% көп болмаса диссоциациялану энергиясының (
Мұндағы
Физика мен химияда қолданылатын энергияның негізгі өлшем бірліктері арасындағы қатынастарда білу өте қажетті:
1 хартри (а. е. э. ) =27, 21 эВ;
1 эВ=23, 06 ккал/моль;
1 ккал/моль=4, 18 кДж/моль;
1 кДж/моль=83, 6 см -1 [6] .
Жартылай эмпирикалық әдістер көрсетілген мәселелерді шешу мүмкіндігі болып табылады, және ab initio әдістерінен келесі маңызды ерекшеліктермен өзгешеленеді:
-екіэлектронды интегралдардың жалпы мөлшері қысқаратын жақындасулар енгізіледі
-кейбір екіэлектронды интегралдарды және де бірэлектронды интегралдарды және жабу интегралдарын есептейді, ал эксперименттің берілгендеріне сүйене отырып бағалайды.
Шредингердің молекулалық теңдеу шешуінің көзқарасынан, принципиалды түрде, жартылай эмпирикалық және эмпирикалық емес әдістерге өзара ерекшеленбейді. Жартылай эмпирикалық әдістер үшін ab initio әдістері үшін де қолданылатын есептеудің жалпы сұлбасы тән. Оның ерекшелігі мынада- есептеудің әр сатысы айтарлықтай жеңілдетіледі.
Көрсетілген ерекшеліктер жартылай эмпирикалық әдістердің артықшылықтарын да, кемшіліктерін де анықтайды. ab initio әдістерімен салыстырғандағы негізгі артықшылықтар төменде көрсетілген:
-есептеу жылдамдығы бірнеше ретке жоғарлайды
-химиялық қосылыстардың (негізінде органикалық) бөлек кластары үшін жартылай эмпирикалық әдістермен молекулалардың кейбір сипаттамаларының есептеу нақтылығын ab initio әдістермен салыстырғанда төмен емес және көптеу болуы мүмкін. Бұл жартылай эмпирикалық әдістерді параметризациясы шынайы қосылыстардың анықталған сипаттамаларының эксперименталды мәндері бойынша жүргізілуіне байланысты, және әрине бұл мәндер жоғары дәлдікпен жүргізіледі. Есептеу уақытының бағалануы интегралдардың есептелуін ғана есепке алады. Шын мәнінде әдістің күрделену кезінде есептеудің реалды күрделенуі қосалқы математикалық операциялардың күрделенуіне байланысты одан да жоғары болады. жартылай эмпирикалық әдістер шектеулерінің оның артықшылықтары сияқты түбірлер бар. Мұндай ерекшелік квантты химияның барлық есептеу әдістері үшін тән және «есептеу дәлдігі»-«есептеу жылдамдығы» параметрлерінде едәуір оптималды қатынастың біркелкі таңдауының мүмкінсіздігімен шартталған. Барлық жартылай эмпирикалық әдістер үшін келесі кемшіліктер тән:
-кеңейтілген ( биэкспоненциалды немесе одан да күрделі) базисте ab initio әдістерімен салыстырғанда жартылай эмпирикалық әдістердің есептеу дәлдігі төмен болады;
-берілген жыртылай эмпирикалық әдіспен қанағаттанарлық дәлдікпен зерттеліне алатын объекттер қатары және де физикалық сипаттамалардан таңдау параметризация сұлбасының осы әдісінде қолданылған ерекшеліктерімен шектелген.
Әдетте жартылай эмпирикалық әдістер органикалық қосылыстар есептеулері үшін қолданылады. Металлоорганикалық, онымен қатар комплексті қосылыстардың қарастырылуы параметризацияның арнайы сұлбаларын талап етеді. Әрбір нақты әдістің шектеулері төменде қысқаша қарастырылатын болады;
-алдыңғы кемшілік және де жыртылай эмпирикалық әдістердің көптеген жақындасуларының «физикалық еместігі» осы әдістердің шегінде қиындау және көбінесе қасиеттердегі аномалиялардың болуын болжап және түсіндіріп, қарастырылатын қатардың қосылыстары үшін тән емес, жаңа қасиеттерінің пайда болуының себебі болады.
Басқаша айтқанда, жартылай эмпирикалық әдістер химик-практикант үшін жақсы ізденіс көзі болып табылады, ол күрделі экспериментсіз зерттелетін жүйенің қасиеттерін бағалауға мүмкіндік береді, ал жаңа қасиеттерді түсіндіру мен болжауға талпынатын химик-теоретик үшін аз жарамды.
Аталып кеткен артықшылықтар мен кемшіліктерді ескере отырып жартылай эмпирикалық әдістердің практикалық қолданысының жетістігі түзу есептеуге келетін, объекттер мен қасиеттер қатарына түсетін шектеулердің және әр әдістің параметризация сұлбасының және жақындасулардың ерекшеліктерін білумен байланысты болады. әрі қарай олардың қиындығының өсу ретінде нақты әдістерді қарастырамыз [7] .
Тығыздықтың функционал теориясы (ағылш. Density functional theory, DFT) -кванттық физика мен кванттық химияда көптеген бөлшектердің жүйелерінің электронды құрылысының есептеу әдісі. Жеке түрде молекулалардың және конденсирленген қосылыстың электрондық құрылымын есептеуге қолданылады. Сандық химия мен сандық физикада едәуір кең тараған және универсалды әдістердің бірі болып табылады.
Тығыздық функционалы теориясы әдісінің ашылуына 1927ж. Л. Томас пен Энрико Фермимен дамытылған Томас-Ферми моделі ықпал етті. Олар электрондардың ядромен және өзара әрекеттесуінің потенциалды энергиясының электронды тығыздығының функционалы түрінде көрсетілген, атом энергиясын оның кинетикалық энергиясының жалпы саны ретінде есептеген әрекеттесу энергиясы да электронды тығыздық арқылы анықталған болатын.
Квантты механиканың дамуында ойнаған Томас-Ферми моделінің рөліне қарамастан оның дәлдігі жеткіліксіз болды, өйткені Хартри-Фок әдісіне қарағанда ауысу әрекеттесі ескерілмейді. 1928 ж. Поль Дирак оған ауыспалы әрекеттесуді сипаттайтын жүктемені қосып Томас -Ферми моделінде энергия функционалын дәлелдеді.
Тығыздықтың функционалының теориясы классикалық болған Томас -Ферми моделінде базаланғанымен, оған сенімді теоретикалық түсіндіру тек қана Хоэнберг-Кон (осылай Пьер Хоэнбергтің (Pierre Hohenberg) және Уолтер Конның (Walter Kohn) аттарына берілген) теоремаларының формулалауымен жүргізілген. Бірінші теоремада атомды ядролардың сыртқы потенциалында болатын электронды жүйе астының негізгі күйінің тығыздығы мен ядролардың өз потенциалы арасында өзара біркелкі сәйкестік бар деп айтылады. Бірінші теория пайда болу теориясы болып табылады және осындай сәйкестіктің құрылыс әдісін бермейді.
Екінші теорема тығыздық функционалы үшін формулаланған квантты механиканың вариациялық принципі болып табылады және электронды тығыздық функционалы ретінде жазылған электрондық жүйе асты энергиясының негізгі күй энергиясына тең минимумы бар. Бастапқы кезден Хоэнберг -Кон теоремалары магнитті өріс қатысынсыз электрондық жүйе астының негізгі күйі үшін ғана формулаланған болатын. Олар уақытқа тәуелді енгізу жолымен жалпыланған болуы мүмкін, ол үшін қозған элетрондар күйінің есептеуі үшін формализмді қолдануға болады.
Электрондық құрылымды анықтайтын дәстүрлі әдістері, оның ішінде Хартри-Фок әдісі және оның туындылары жүйені көнпэлектронды толқынды функцияның көмегімен сипаттайды.
Тығыздықтың функционал теориясының негізгі мақсаты- электрондық жүйе астының сипаттауы кезінде көпэлектронды толқындық функцияны электрондық тығыздықпен алмастыру. Бұл тапсырманы айтарлықтай жеңілдетеді, өйткені көпэлектронды толқынды функция Nэлектрондардан әрқайсысына 3 кеңістіктік координатадан -3N ауыспалыдан тәуелді, ал тығыздық -тек үш кеңістіктік координаталардың функциясы [8] .
Тығыздықтың функционал теориясының әдісі 1970ж. бері қатты дене физикасында есептеулер үшін кеңінен қолданылады. Бірқатар жағдайда жай локалды тығыздықтың жақындасуын қолданғанда эксперименталды берілгендерге сәйкес келетін қанағаттанарлық нәтижелер береді, әдістің есептеу қиындығы басқа есептеулердің квантты механикада көптеген бөлшектердің мәселесіне қатысты жоғары емес. Дегенмен, 1990 ж. ауыспалы және корреляциялық әрекеттесулер сипаттамаларында көрінетін алға басу жүрмегенше, бұл әдіс квантты химия облысында есептеулер үшін жеткіліксіз дәл болатын. Қазіргі уақытша тығыздықтың функционал теориясы әдісі екі облысына да негізгі жағдай болып табылады. Теорияның процесіне қарамастан молекулааралық нүктелердің сипаттамаларына әдістің қосындысында әлі де мәселелер көп, әсіресе Ван-дер-Ваальстік күштері мен дисперстілеу әрекеттесулердің және де жартылай өткізгіштерге рұқсат етілмеген зонаның енінің есептеулерінде.
Қарастырылатын жүйенің құрамына кіретін, ядроның, электронның құрылымының көптеген есептеулерінде қолданылатын Борн-Оппенгеймер болжамына сәйкес қозғалмайтын болып табылады [9] .
Тығыздықтың функционал теориясы әдісінің формализмі векторлық потенциалдың, оның ішінде, магниттік өріс қатысында бөлу жағдайында бұзылады. Бұл жағдайда электрондық тығыздық пен (атом ядроларының) сыртқы потенциал арасындағы өзара біркелкі сәйкестік болмайды. Магниттік өріспен байланысты эффекттерді есепке алу үшін формализмді жалпылау мүмкіндіктері екі түрлі теорияға бөлінеді: тоқ тығыздығы векторын есепке алу мен тығыздық функционалы теориясы және магниттік өрісті есепке алумен тығыздықтың функционал теориясы. Екі жағдайда да алмасу-корреляциялық энергиясының функционалы жалпыланады және тек электрондық тығыздықтан ғана тәуелді болмайды. Vignale мен Rasolt дамытқан бірінші жағдайда электрондық тығыздықтан басқа ток тығыздығы да аргумент болып табылад. Екінші жағдайда (Salsbury, Grayce, Harris) функционалдың қосымша аргументі болып магниттік өріс түрінен тәуелді болады. екі әдісі үшін де локалды тығыздық болжамынан алыс алмасу -корреляциялық энергиялық есептеу жеткілікті қиын болуын практикада Кон-Шэм әдісі зерттеу мақсатына байланысты бірнеше түрлі тәсілдермен қолдануы мүмкін. Қатты дене физикасы есептеулерінде жалпақ толқын базисімен қоса локалды тығыздық болмауы осы күнге дейін кеңінен қолданылады. Молекулалардың электрондық құрылымын есептеу үшін функционал үшін едәуір күрделі теңдеулер қажет. Осылай алмасу- корреляциялық әрекеттесуі өлшеу үшін жақындастырылған функционалдардың үлкен саны химия есептеуі үшін дамыған. Олардың кейбіреулері біркелкі кеңістіктік электрондық газдың теориясына қарама-қайшы келеді, бірақ дегенмен, электрондық газға ауысу кезіндегі шекте локалды тығыздық жақындасуында қиылысу керек.
Физикалық есептерді санау үшін көбінесе Perdew - Burke - Ernzerhof нақтыланған алмасу моделі қолданылады, алайда, ол газды фазада молекула есептеулеріне сәйкестендірлген, калометриялық параметрлерде қателіктерге ұшырайтыны белгілі.
Квантты химия есептеулерінде BLYP (Becke, Lee, Yang, Parr) деп аталатын ауысу функционалының түрі кең таралған болып табылады. Гибридті функционалда негізделген B3LYP болжамы одан да кең таралған, ондағы алмасу энергиясы Хартри-Фок әдісімен алынған дәл нәтижелермен есептелінеді. Жалпы айтқанда, тығыздықтың функционал теория әдісінің қазіргі жағдайы басқа теориялармен немесе эксперимент нәтижелерімен салыстырмай тұрып, есептеу қателігін табу мүмкін емес [10] .
Молекулалық механиканы ХХ ғ. 60-жылдары Т. Хилл мен А. И. Китайгородский тапқан. Терминді 1985ж. Л. Бартелло ұсынған.
Молекулалық механика - молекулалардың геометриялық сипаттамаларының және энергиясын анықтаудың есептеу эмпирикалық әдісі. Ол молекула Е энергиясы байланыс ұзындықтарына r, валентті бұрыштарға α және екіқабырғалы (торсиондық) бұрыштары t жатқызылуы мүмкін қосымша сомамен белгіленуі мүмкін деген болжамда негізделген. Одан былай, энергияның жалпы теңдеуінде әрқашан валентті байланыспаған атомдардың ван-дер-ваальстік әрекеттесуін көрсететін E вдв мүшесі және эффективті атомдық зарядтардың болуын шарттайтын және атомдардың электростатикалық әрекеттесуін ескеріп отыратын Е кул мүшесі болады. Молекуланың жалпы энергиясы келесідей сомамен беріледі:
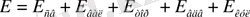 (9)
(9)
Бірінші екі қосылғыштың есптеуі үшін көбінесе мехникадан белгілі Гук заңын қолданады (осыдан әдіс атауы) :
Энергия Е тор үшн аналитикалық теңдеу, мысалы С 2 Н 6 молекуласы үшін келесідей болады:
мұндағы V 3 -ішкі айналудың потенциалды шегі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz