Операторлық модельдер: үздіксіз сызықты уақытша динамикалық жүйелердің аналитикалық және құрылымдық сипаттамасы


Операторлық модельдер.
Динамикалық жүйе математикалық модель процестердi жүйеде даму бiрмәндi анықтайтын математикалық символдардың жиынтығы атау қабылданған, яғни қозғалыс . Пайдаланылатын символдар байланысты бұл ретте аналитикалық танып бiледi және графоаналитикалық үлгiлер. Аналитикалық үлгiлер әрiптiк символдардың көмегiмен салады, осы уақытта графоаналитикалық график түрiнде белгiлер қолдануға жол бередi.
Байланысты түрiндегi сигнал үздiксiз танып бiлiнедi және систем дискреттi үлгiлер. Пайдаланылатын операторлар байланысты - сызықты және сызықты емес, сонымен бiрге уақытша және жиiлiк үлгiлерi. Уақытшаға аргументке уақытты (үздiксiз немесе дискреттi) болып көрiнген үлгiнi жатады. Бұл дифференциалды және айқын түр жазылған
 айырма теңдеулер немесе операторлық пiшiнде. Жиiлiк үлгiлерi аргументi тиiстi сигналды жиiлiктi болып көрiнген операторларды пайдалануды ескередi, яғни Лапластың операторлары, Фурье және тағы басқалар.
айырма теңдеулер немесе операторлық пiшiнде. Жиiлiк үлгiлерi аргументi тиiстi сигналды жиiлiктi болып көрiнген операторларды пайдалануды ескередi, яғни Лапластың операторлары, Фурье және тағы басқалар.
Бөлiм бұл систем үздiксiз сызықты уақытша динамикалық үлгiлердi қаралады.
Динамикалық жүйенiң сигналдары байланыстың сипаттамасы кiрiс және шығатын (ҒҒ ) кiру-шығу үлгi -. Мұндай сипаттамада қажеттiлiк жеке блоктердi мiнез-құлық қарастыру кезiнде көрiнiп қалады және, (ОБ ) басқарушы объект жеке алғанда, сол сияқты барлық басқару жүйесi негiзiнен. Блок математикалық сипаттауда айырмашылық және басқару жүйесi маңызсыз, бiрақ (см. п. 1. 5) әр түрлi белгiлердiң пайдалануы талап етедi. Осылай, (t ) y* тағайындаушы әсер сауы кiретiн сигналын болып көрiнедi, ал демалыс - (t ) y айнымалы. (t ) белгi x2 блоктердi сипаттамада жиi пайдаланады және (t ) x1, сәйкесiнше сәйкесiнше. Белгi ендiгәрi пайдаланып қаламыз, кiретiн сигнал (t ) u басқарушы әсер болып көрiнген басқарушы объект тәнбiз, ал (t ) y реттелетiн айнымалы шығумен.
2. 1. 1. Аналитикалық үлгiлер. (мұнда - басқарушы объект) бiр арналы динамикалық жүйесi кiру-шығуы сызықты үлгiсi мүмкiн түрдiң таныстырылған кәдiмгi дифференциалды теңдеу болу:
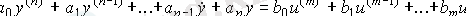 [ М1 ],
[ М1 ],
мұндағы где
a
i
, b
i
-коэффициенттері (
модели
),
a
0
 0, b
0
0, b
0
 0, n
- моделдің реті,
0
0, n
- моделдің реті,
0
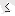 m<n
. [M1] теңдеуі кіру байланысы
m<n
. [M1] теңдеуі кіру байланысы
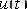 және оның туындысы
және оның туындысы
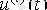 шығу байланысы
y
(
t
) және олардың туындысы
шығу байланысы
y
(
t
) және олардың туындысы
 кейбір уақытша аралықтағы және т. б.,
кейбір уақытша аралықтағы және т. б.,
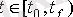 .
.
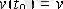 ,
,
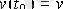 , . . . ,
, . . . ,
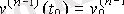 мәндері бастапқы мәнді, ал
r = n - m
мәндері бастапқы мәнді, ал
r = n - m
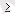 1
- сандары моделдің дәрежесіне қатысты.
1
- сандары моделдің дәрежесіне қатысты.
Стационарлық жүйе ерекшеленеді, өзгеріссіз параметрлік мәндер үшін :
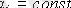 ,
,
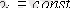 және мүмкін
және мүмкін
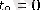 , және стационарлы емес моделдер, мұндағы функция параметрлері уақыт және т. б.
, және стационарлы емес моделдер, мұндағы функция параметрлері уақыт және т. б.
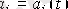 ,
,
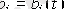 . Мұндай жағдайда
. Мұндай жағдайда
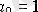 , теңдеу келтірілген деп аталады.
, теңдеу келтірілген деп аталады.
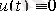 , жүйе автномдық деп аталады. Описание автономной системы дается
однородным
дифференциальным уравнением вида
, жүйе автномдық деп аталады. Описание автономной системы дается
однородным
дифференциальным уравнением вида
 [M1а] .
[M1а] .
[M1] моделі операторлық формада жазылуы мүмкін. Ол үшін дифференциралдық операторды қарастырамыз.
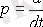 және
және
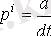 .
.
С учетом введенных обозначений уравнение [M1] теңдеуіндегі мәндерін операторлыұ формаға оңай келтіруге болады
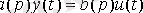 [М2],
[М2],
мұнда дифференциалдық операторы қолданады
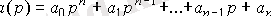 , (2. 1)
, (2. 1)
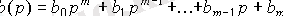 . (2. 2)
. (2. 2)
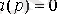 (2. 3),
(2. 3),
[M1] жүйесінң полюсы деп аталады . Дифференциалдық оператор b(p) - сипаттамалық полиномының оң жағы. Теңдеудің түбірі
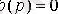 (2. 4),
(2. 4),
т. е. комплекстік сан
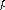
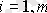 , [M1] нөлдік жүйе деп аталады.
, [M1] нөлдік жүйе деп аталады.
[М2] теңдеуінен y ( t ) және u ( t ) теңдеулері операторлық теңдеуінің түрі :
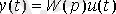 [М3],
[М3],
мұндағы дифференциалдық - интегралдық оператор
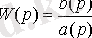 (2. 5)
(2. 5)
[M1] берілетін функция жүйесі деп аталады.
Динамикалық жүйенің дербес жағдайын коэффициенттерімен қарастырамыз
b
0
=b
1
= . . . =b
m-1
=0
.
b
m
=b
 0
жүйесіне қатысты дәреже
r=n-1
,
0
жүйесіне қатысты дәреже
r=n-1
,
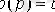 және нөл бар. [M1] теңдеуі төмендегідей түрге енеді
және нөл бар. [M1] теңдеуі төмендегідей түрге енеді
 (2. 6),
(2. 6),
[M2] - теңдеуі
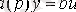 (2. 7),
(2. 7),
Ал [M3] - теңдеуі
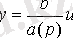 (2. 8) .
(2. 8) .
Пример 2. 1.
Сәйкесінше
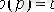 және
және
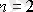 . Дифференуиалдық теңдеу мына түрге ие болады:
. Дифференуиалдық теңдеу мына түрге ие болады:
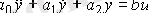
Бастапқы шарттарымен
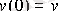 ;
;
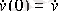 . Здесь
. Здесь
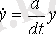 - жыладмыдық шығу. Операторлық модель формасы -
- жыладмыдық шығу. Операторлық модель формасы -
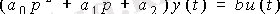 ,
,
Және
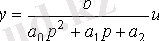 .
.
Теңдеудің сипаттамалық мәні
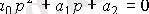
екі түрде түбірі
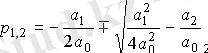 .
.
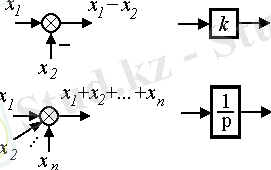
2. 1. 2. Структуалық схемасы. Схеманың элементтері төмендегідей түрде беріледі. (Сурет. 2. 1)
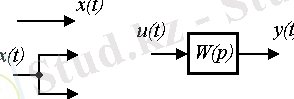
Сурет. 2. 1. Структуралық схеманың элементтері
( x ( t ) , u ( t ) , y ( t ) и т. д. ) и т. д. - сигналдардың әріппен белгіленуі
(например, W ( p ) ) ; - сигналдардың әріппен белгіленуі
Сурет. 2. 2. Қарапайым блог
Пән бойынша негізгі және қосымша әдебиеттер тізіміБаспасы,
шығарылған жылы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz