Полярлық координаталар және Microsoft Excel көмегімен графиктерді құрастыру


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:
«Сәулет» мектеп-лицейі
Ғылыми жоба тақырыбы:
«Қызықты графиктер»
Орындаған: 9 сынып оқушысы
Айбат Арайлым
Мұғалімі: Г. Г. Турганалиева
Тасқала - 2012
Мазмұны
Кіріспе
Менің жұмысымның мақсаты берілген кескіндердің декарттық координаталар жүйесінен полярлық координаталар жүйесіне ауысу формулаларының құрылу принціптерін қарастыру. Сонымен қатар полярлық координаталар жүйесінің артықшылықтарын көрсету. MS Excel бағдарламасында математикалық есептердің графигін тұрғызу үшін моделін құру. Берілген бағдарламаларды жетік меңгерту және басқа пәндермен ұштастыра білу.
Менің ұсынып отырған жобам математика пәнімен ұштастырылып, графика тақырыбын терең және қызықты етіп өткізуге тиімті.
Ғылыми жобамен танысу үшін информатика негіздерін білу қажет. Сондықтанда ғылыми жоба мазмұнын мектепте, гимназия, лицей және техникумдағы математика, физика сабақтарында қолдануға болды.
1. Полярлық координаталар жүйесі
Алғаш рет полярлық координаталар жүйесін біздің ғасырымызға дейінгі ІҮ ғасырда Динострат квадратрисаны зерттегенде қолданды. Одан кейін 1525 жылы А. Дюрера полярлық координаталар жүйесі туралы көптеген жаңалықтар ашты. Ал 1670-71 жылдары И. Ньютон «Флюксий тәсілдерінде» үш мәрте полярлық координаталар жүйесін тікбұрышты координаталар жүйесімен байланыстыратын формула құрады. Осы полярлық координаталар жүйесі туралы нақты түсінік берген Л. Эйлер болатын. Полярлық координаталар жұйесінің термины ХІХ ғасырда пайда болды.
Полярлық координаталар жүйесін жазықтықтағы нүктенің орналасу бағытын келесі элементтер арқылы анықтайды:
- полюс деп аталатын Р нүктесін;
- полярлық ось деп аталатын Р нүктесінен таралған сәулелерді.
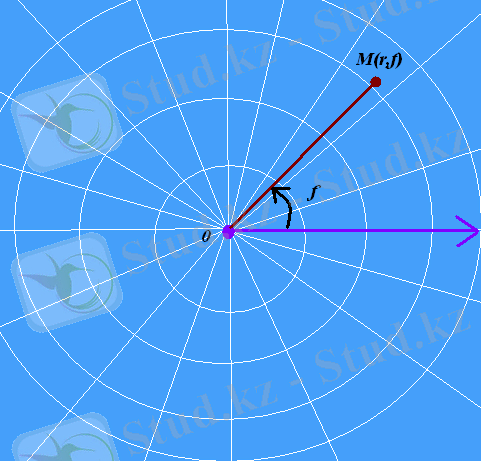 Осыдан кейін М нүктесінің жазықтықтағы орналасуын r және φ нүктелері арқылы табамыз. Осы нүктелерді полярлық координата деп атаймыз. Мұндағы r≥0 М нүктесінен полюске дейінгі қашықтық, ал φ (0≤φ<2π немесе - π<φ≤π) полярлық ось пен сәуленің арасындағы РМ бұрышы.
Осыдан кейін М нүктесінің жазықтықтағы орналасуын r және φ нүктелері арқылы табамыз. Осы нүктелерді полярлық координата деп атаймыз. Мұндағы r≥0 М нүктесінен полюске дейінгі қашықтық, ал φ (0≤φ<2π немесе - π<φ≤π) полярлық ось пен сәуленің арасындағы РМ бұрышы.
Полярлық координата жүйесінде координаталар сызығы r=const=R R радиустың айналымы, ал φ=const сәуле полюсімен сәйкес бағытталады.
Егер Оху декарттық координаталар жүйесін енгізсек, мұндағы координаталар басының О нүктесі Р полюсымен және Ох полюсы полярлық полюсымен сәйкес келсе, онда полярлық (r, φ) және декарттық (х, у) координаттары келесі теңдіктермен байланысады:
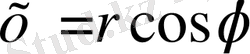 ,
,
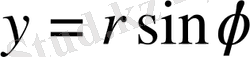 .
.
2. Microsoft Excel программасы көмегімен графиктерді сызу
x=r*cos(φ), y=r*sin(φ) мына формулаларды пайдалана отырып, декарттық координаталар теңдеуін полярлыққа ауыстырамыз:
Тапсырма. Берілген теңдеу бойынша фигура құрастыру
Шығарылуы. Полярлық координаталардағы сызықтың теңдеуiн табамыз.

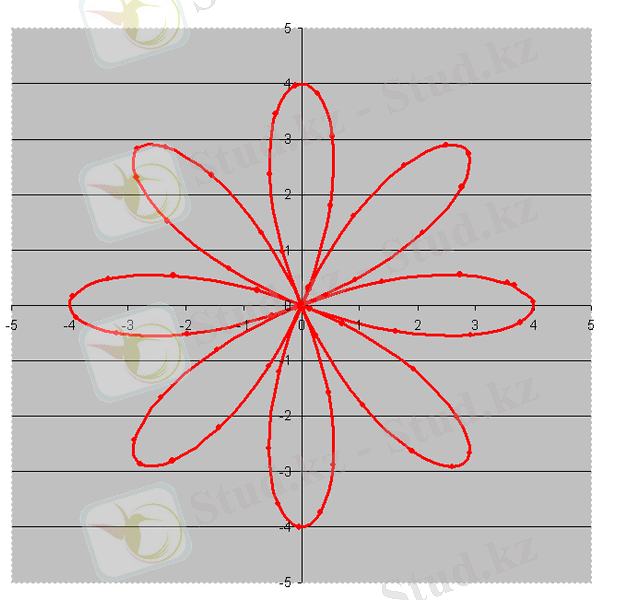
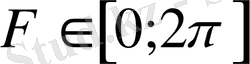 Microsoft Excel бағдарламасы үшін берілген формула: R= 4*COS(3*F)
Microsoft Excel бағдарламасы үшін берілген формула: R= 4*COS(3*F)
Бұрыш
Өзгеру қадамын 0, 1 деп алайық
Зерттеудің үлгісін компьютерде қарастырайық
Деректерді енгізгеннен кейін, оны мына электрондық кесте түрінде көре аламыз:
А20, 1
А3=А2+0, 1
B2=4*COS(3*F)
C2=SIN(А2)
D2=COS(А2)
E2=B2*D2
F2 =В2*C2
Графикті құру үшін E2. . F63 ұяшықтарын белгілеп аламыз, өйткені F аргументі 0, 1-ден 6, 3 радианға дейін өзгереді.
Шығатын нәтиже
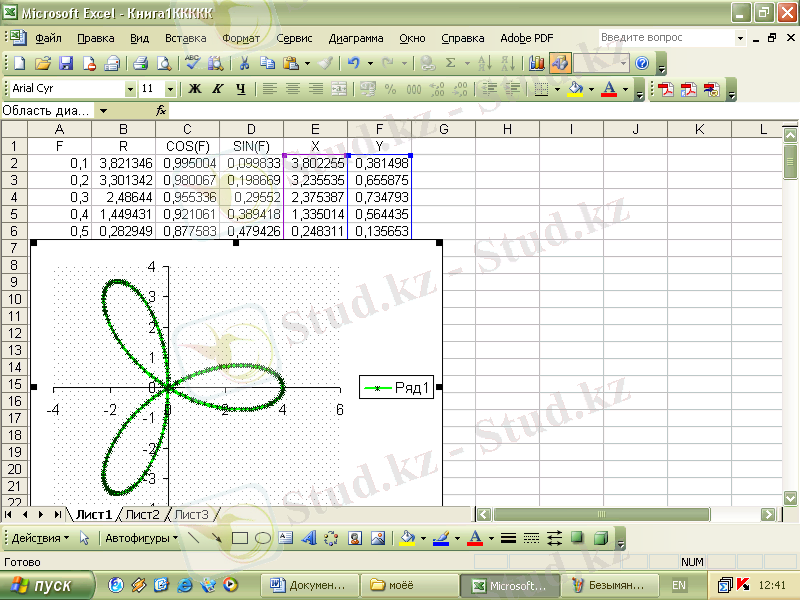
Гранди раушангүлі
 Тапсырма.
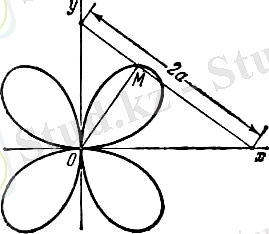
Қиылған 2а кесіндісі шеткі нүктелері остік координатада жататындай қозғалады. Координаталар басынан кескінге дейін жүргізілген М перпендикуллярдың траекториялық теңдеуін құру керек.
Тапсырма.
Қиылған 2а кесіндісі шеткі нүктелері остік координатада жататындай қозғалады. Координаталар басынан кескінге дейін жүргізілген М перпендикуллярдың траекториялық теңдеуін құру керек.
Берілген тапсырманың шешуі теңдеу арқылы шығарылады (бұл төртжапырақты раушан гүлінің теңдеуі) .
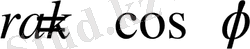 Полярлық координатасында бұл тапсырманы мына теңдеулер арқылы шығарылады: немесе
Полярлық координатасында бұл тапсырманы мына теңдеулер арқылы шығарылады: немесе
РАУШАН ГҮЛІНІҢ ТҮРЛЕРІН ТАЛДАУ
«Раушан гүлі» - радиусы А болатын шеңбердің ішінде орналасады. Оның жапырақтарының саны k модуліне байланысты:
1. Егор модуль k-бүтін сан болса, раушан гүлі k жапырақтан тұрады, тақ болғанда k, жұп болғанда 2k жапырақ болады.
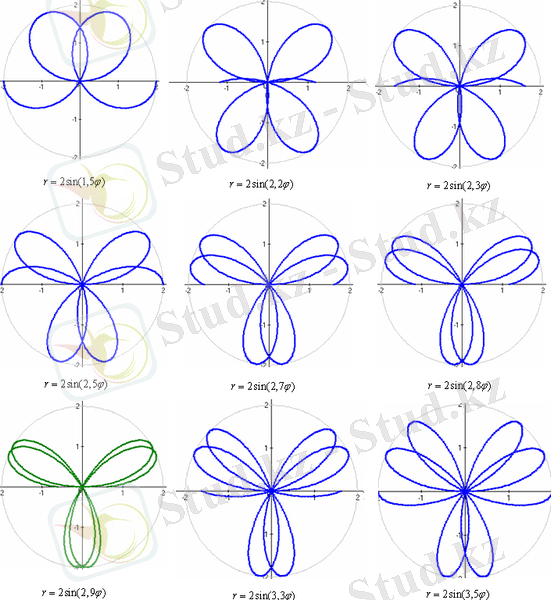
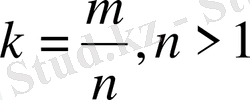
2. Егер k саны -ге тең рационал сан болса, m және n сандары тақ болған жағдайда раушан гүлі m жапырақтан тұрады, ал m және n сандарының біреуі жұп болса раушан гүлі 2 m жапырақтан тұрады.
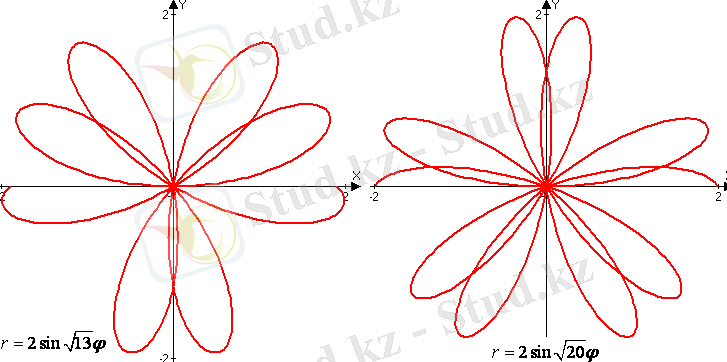
3. Егер модуль k иррационал сан болса, раушан гүлі сансыз көп жапырақтан тұрады, және бір-біріне тығыз орналасады.
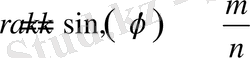 «Раушан гүлінің түрленуі»
«Раушан гүлінің түрленуі»
(MS Excel, Turbo Pascal 7. 0 тілдері арқылы шығарылуы)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz