Логикалық элементтер
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:
КІРІСПЕ
Ғылыми-техникалық революция мен оның өсу қарқыны көп жағдайда электрониканың дамуымен анықталды. Электроника-электрондардың электромагниттік өрістерімен өзара әсері жөніндегі ғылым. Электроника электромагниттік энергияның түрленуін, күшеюін, электромагниттік тербелістердің қабылдануын, инфрақызыл, вакуумдық, рентгендік спектрлердің шашырауын, информацияны беру, өңдеу және сақтауды, сондай-ақ оларды әртүрлі процесстерді басқаруға қолдануды қарастырады. Бұл электрониканың ғылымда, техникада, күнделікті тұрмыста кеңінен қолдануына саяды. Электроника вакуумдық, қатты денелік және кванттық болып бөлінеді. Қатты денелік электрониканың негізгі бөлімі жартылай өткізгіштер, олардың қасиеттері мен қолданылуы жайлы ілім болып табылады, сондай-ақ жартылай өткізгішті приборларға диодтар, транзисторлар, тиристорлар, оптондар, әсіресе, ЭВМ-ге негізделген интегралдық схемаларды пайдалану әдістері енеді.
Қазіргі күндері сандық қондырғылар аналогты қондырғыларды ысырып, техникада өз орнын тауып келеді. Бұл күндері сандық қондырғылардың ішінде көптеп қолданылатын түрлеріне: триггерлер, мультиплексорлар, демультиплексорлар, шифраторлар, дешифраторлар, санағыштар, сумматорлар жатады. Сандық қондырғылар аналогты қондырғылардан айырмашылығы мұнда сиганлдар аналогты сандақ түрлену құрылғысынан және сандық индикаторлардан тұрады. Аналогты сандық түрлену процесі өзі үш кезеңнен тұрады. Бірінші процесс дискреттеу процесі, екінші процесс квантталу процесі болса, үшінші процесс кодталу процесс болып табылады. Яғни мұнда қарапайым сигнал екілік сан түрінде түрленіп, сандық индикаторлар арқылы позициялық сан түрінде беріледі.
II. Негізгі бөлім
2. 1. Логикалық элементтер
Кәдімгі алгебрадан басқа арнайы алгебра бар. Оның негізін ХІХ ғ. математигі Дж. Буль салған. Бұл алгебра пікірлерді есептеумен айналысады.
Оның ерекшелігі дискреттік құрылғылардың жұмысын сипаттауға қолдану болып келеді. Ондай құрылғылар қатарына есептеу техникасы және автоматика құрылғыларының бір классы жатады.
Мұнда алгебраның өзі құрылғының үлгісі рөлін атқарады. Ол көрсетілген типтегі еркін құрылғының жұмысы осы алгебраның көмегімен қандай да бір жағынан тек қана сипатталуы мүмкін дегенді білдіреді. Шындығында нақты құрылғы физикалық логика алгебрасында сипатталғанна бөлек жұмыс істейді.
Логика алгебрасының функцияларына қатысты бірнеше синонимдер бар:
- логикаалгебрасының функциялары;
- ауыстырып қосқышфункциялары;
- бульдікфункциялар;
- екілікфункциялар.
Қажеттілігінше бұл синонимдердің барлығын пайдаланамыз.
Аргументтердің қандай да бір жиынын қарастырайық:
<X 1 , X 2 , X 3 , . . . Х i , . . . X n >
және де аргументтердің әрқайсысы басқаларынан тәуелсіз екі мүмкін мәннің біреуін қабылдайды деп келісеміз.
X i = {0, 1}
Бір және екі айнымалыға тәуелді бірнеше бульдік функцияларды қарастырайық.
Ол үшін аргументтердің барлық терімдеріне оның мәндерін беру керек.
Екі аргументке тәуелді барлық ЛАФ-ын қарастырайық та оларды бір кестеге жазайық:
Функция
№
f(X 1 , X 2 ) =0
f(X 1 , X 2 ) = X 1 & X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 · X 2
f(X 1 , X 2 ) = X 1 X 2
X 1 Δ X 2
f(X 1 , X 2 ) = X1
X 2 Δ X 1
f(X 1 , X 2 ) = X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 + X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 ~X 2
f(X 1 , X 2 ) =^X 2
f(X 1 , X 2 ) =X 2
f(X 1 , X 2 ) = X 2
X 1
f(X 1 , X 2 ) =^X 1
f(X 1 , X 2 ) = X 1
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 X 2
f(X 1 , X 2 ) =1
Логикалық элементтер, ЭЕМ-де логикалық функцияларды іске асыру. Логикалық элементтердің функционалды -толық жүйелері.
Қандай да бір күрделі пікірге қандай мағыналық мазмұн енгізуге болатынын 2 аргументті ЛАФ-ы мысалында қарастырайық.
Инверсия. Х ЕМЕС немесе ' Х ' -ті теріске шығару деп оқылады.
Мысалға мынадай пікірді алайық: А=<Киев-Франция астанасы>, онда күрделі А ЕМЕС пікірі А дұрыс емес екенін, яғни <Киев-Франция астанасы> емес екенін білдіреді.
Қарапайым пікірлерден күрделі пікірлерді байланыстарды қолданып құруға болады.
Логикалық байланыстар- аргументтері қарапайым пікірлер болып келетін ЛАФ-ры.
Конъюнкция. Екі пікірді алайық:
А=<Москва - РФ астанасы>
В=<екі-екім төрт>
онда А & В күрделі пікірі ақиқат болады, өйткені бұл екі пікір де ақиқат.
Егер ақиқат пікірге '1' мәнін ал жалғанға '0' мәнін жазсақ онда пікірді көбейтінді деп айтуға болады. Бұл жағдайда конъюнкция үшін ақиқаттық кестесі көбейту кестесіне сәйкес келеді.
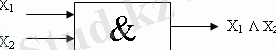0
Конъюнкция функциясы екі пікір бір уақытта ақиқат болған жағдайда ғана ақиқат.
Дизъюнкция. Бір күрделі пікір оған кіретін пікірлердің кем дегенде біреуі ақиқат болған жағдайда ақиқат болады.
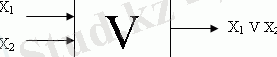f
1
(X
1
, X
2
)
X 1 НЕМЕСЕ X 2 деп оқылады:
Еркін құрылғыны синтездеу техникалық (физикалық) есебі ЛАФ-ын құру математикалық есебіне әкелінеді.
Еркін ЛАФ-ын құру үшін байланыстың қандай көлемі қажет деген сұрақ әрине пайда болады. Бұл сұрақтың жауабы бірмәнді емес. Мысалы f 0 (0 тұрақтысы), f 15 (1 тұрақтысы) функциялары көмегімен еркін ЛАФ-ын құруға болмайтынын көреміз. Оны тек инвертордың көмегімен құру да мүмкін емес. Бірақ оны f 7 , f 1 , f 10 немесе f 7 , f 1 , f 12 көмегімен құруға болатыны анық.
Бұл элементар ЛАФ-ның жиыны
конъюнкция, дизъюнкция
және
теріске шығарудың
базисі
деп аталады. ЛАФ-ын математикалық ұйымдастыру кезіндегі ең кең тараған базис. Бұдан басқа базистер де бар:
, +, 1,
Сол сияқты бір элементті базистер бар: f 8 - Пирса тілсызығы, f 14 - Шеффер штрихы, ЖӘНЕ-ЕМЕС, НЕМЕСЕ-ЕМЕС.
Құрылғының техникалық синтезі үшін нақты құрылғыны құруға мүмкіндік беретін, ЛАФ-ры базис құратын элементтердің қандай да бір терімі болуы керек. Бірақ, айтып кеткендей ЛАФ-ын синтездеу есебі - идеал модель.
Логика алгебрасы функцияларын минимизациялау және оны қарастырғандағы шектеулер.
Мүлтіксіз дизъюнктивті қалыпты форма (МДҚФ) жазудың тиімді формасы болмайтынын мысалда көрсетейік:
f(Х
1
, Х
2
) = Х
1
Х
2
Х
1
Х
2
Х
1
Х
2
=Х
1
Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Сонымен құрылғыны синтездеу есебі ондағы жабдықтарды азайту есебімен толықтырылуы керек. Математикалық көзқарастан бұл есеп минималды ЛАФ-ын құру есебі.
Минималды ЛАФ-ы дегеніміз бастапқы формадағыдан аз әріптер санына тұратын форма.
Егер қандай да бір терімде f а
1
мінін қабылдаса, ал
а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
функциясының а
2
мәнін жабады деп айтады.
ЛАФ-ын минимизацилаған кезде бастапқыға қарағанда аз әрпі бар форманы алуға тырысады.
Дизъюнктивті қалыпты формаға қатысты бұл форманы қысқартылған дизъюнктивті қалыпты форма (Қысқ. ДҚФ) деп атайды. ҚДҚФ құрудың мәні оның құрамына бастапқы функцияның бір емес бірнеше бірлігін жабатын бірліктері бар элементар көбейтулер кіреді.
ҚДҚФ - ға кіретін әрбір элементар көбейтінді функцияның тек бір бірлігін жабады.
ҚДҚФ-ны алу тәртібі төмендегідейболуы мүмкін.
1. Бастапқы МДҚФ-ның бірліктерінің конституенттеріне барлық толық емес жабыстыру операцияларын орындау. (n-1) -рангті көбейтінділер шығады. Қалған жапсырылмаған бірліктің конституенттері келешектегі жабыстыруларға қатыса алмайды.
2. Алынған барлық бірлік конституенттерімен көбейтінділерінің жабуын жүргізу. Кейбір бірлік конституенттерінің бөлігі шектеледі.
3. 1) және 2) операцияларын мүмкін болғанша жүргізу.
Мысал 1.
f(Х 1 , Х 2 ) = Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Егер толық жабыстыру операциясын қолдансақ онда:
f(Х 1 , Х 2 ) = Х 1
Х 1 Х 2
немесе
f(Х 1 , Х 2 ) = Х 1 Х 2
Х 2
яғни, операцияны ары қарай жүргізуге мүмкіндік жоқ.
Енді толық емес жапсыру операциясын қолданайық:
f(Х 1 , Х 2 ) = Х 1
Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Х 2 = Х 1
Х 2
Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Х 1 , Х 2 - қарапайым импликанттар
Х 1 Х 2 , Х 1 Х 2 , Х 1 Х 2 - бірліктің коституенттері
Енді жою операциясын жүргізе аламыз:
Х 1 Х 1 -ді жояды, Х 1 Х 2 , Х 1 Х 2
Х 2 Х 2 - ні жояды, Х 1 Х 2 , Х 1 Х 2
Яғни Қысқ. ДҚФ
f(Х
1
, Х
2
) = Х
1
Х
2
біздің жағдайымызда бұл минималды форма
Толығымен анықталған функцияларды минимизациялау.
Нақты құрылғының жұмысы көп жағдайда толығымен анықталмаған функция көмегімен сипатталады, өйткені кіру сигналдарының кейбір комдинациялары берілмейді немесе рұқсат етілмеген болып келеді.
Толық анықталмаған функция аргументтердің кейбір терімдерінде мәндері еркін болатын ауыстырып қосқыш функция болады (яғни, “0” немесе “1”-ге тең) .
f(x
1
, x
2
, . . . x
n
) функциясы аргументтердің “p” терімінде анықталмаған болсын. Онда толық анықталған
(x
1
, x
2
, . . . x
n
) функциясын f(x
1
, x
2
, . . . x
n
) функциясына эквивалентті деп санаймыз, егер оның мәндері f(x
1
, x
2
, . . . x
n
) анықталған терімдердегі мәндермен сәйкес келсе.
f(x 1 , x 2 , . . . x n ) - ға эквивалентті әр түрлі 2 р функциялары бар екені анық.
f(x
1
, x
2
, . . . x
n
) - ді минимизациялау есебі дегеніміз формасы қарапайым эквивалентті
(x
1
, x
2
, . . . x
n
) - ді таңдау.
Толығымен анықталмаған функцияларды Вейч диаграммаларының көмегімен минимизациялау көрнекті және ыңғайлы түрде минималды формаларды іздеп табуға көмектеседі.
Мысал: f(x 1 x 2 x 3 x 4 ) функциясын қарастырайық та оның минималды формасын табайық. Вейч диаграммасын келесі ережелерге сәйкес толтырайық: бірліктің конституенттеріне сәйкес келетін ұяшықтарға бірлерді қоямыз, жоқ конституенттер үшін - нөлдерді, қалған ұяшықтарға «*» (жұлдызша) - анықталмағандық символын қоямыз.
x 1 ^x 2 x 3 x 4 , ^x 1 ^x 2 x 3 x 4 , ^x 1 ^x 2 x 3 ^x 4 конституенттері үшін ұяшықтарға анықталмағандық символы орнына бірліктерді қойған дұрыс, өйткені ол жағдайда ^x 2 x 3 көбейтіндісімен жабылатын 2 - ші рангті дұрыс конфигурация құрылады.
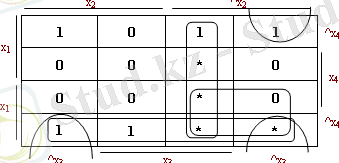
Дәл сол сияқты ^x 1 ^x 2 ^x 3 ^x 4 ұяшықтарына бірліктерді қою керек.
Сонымен, f
min
(x
1
x
2
x
3
x
4
) = ^x
2
x
3
^x
1
^x
4
^x
3
^x
4
^x
1
^x
2
.
Негізгі әдебиет: 1, 2, 3, 4, 8
Қосымша әдебиет: 11, 12, 13
ЭЕМ-ді құрудың классикалық негіздері.
Электронды есептеу машиналарды құру негіздері көрнекті ғалымдармен өткен ғасырдың 30-шы - 40-шы жылдары салынған. Олар ағылшын математигі Алан Тьюринг және американдық Джон Нейман.
Тьюринг машинасы. 1936ж А. Тьюринг абстрактты есептеу машинасы түсінігін қалыптастырды. Онымен бір уақытта Э. Пост (АҚШ) бірақ ашық формада емес, дәл соны істеді. Тьюринг машинасы (ТМ) шын әрекет ететін құрылғы болмаса да оны қазіргі кезде де «алгоритм», «есептеу процесі» деген түсініктердің маңызын айқындау үшін негізгі үлгі ретінде қолданады.
«Бірмәнділік емес» логикалық функциясын тьюринг машинасында есептеу бағдарламасының жазылу мысалы:
y=x
y логикалық функциясын есептеу мысалы
Нейман автоматы. Ақпаратты өңдеу принципі бойынша Нейман ұсынған есептеу құрылғысы ( Нейман автоматы - НА) Тьюринг машинасынан маңызды айырмашылығы бар.
Тьюринг машинасының маңызды ерекшелігі - әрбір тактте ақпаратты түрлендіру тек қана бір ұяшықта жүргізіледі, ал қалғандары «головканың» келгенін тосады, бірақ параллель жұмыс істеу мүмкіндігі жиі туады.
Жалпыға бірдей сыртқы жады (лентасы) бар бірнеше Тьюринг машинасын қолдану - қарапайым шешімі әрқашан мүмкін емес, өйткені жадының бір ұяшығына бір уақытта қатынау кезінде конфликт тууы мүмкін.
Нейман автоматында
бір уақытта өңделетін ұяшықтардың саны, әрбір кезеңде шекті болып, шексіз өсе беруі мүмкін.
Нейман элементі
(НЭ) - бұл оның әрбір тактте оның алфавитін құрайтын r
i
R шекті күй санының бірінде болатын құрылғы. НЭ - де екі кіру арнасы бар: оң және сол; әрбір t тактінде оның әрқайсысына R - ден бір күй келіп түседі.
2. 2. Шифраторлар.
Цифлық логикалық құрылғылардың функционалдық түйіндері екіге бөлінеді: комбинациялық және тізбектелген. Комбинациялық типті функционалдық түйіндер деп шығыс сигналдары кез келген уақыттың дискретті мезетінде дәл осы кезде кірісте тұрған бірмәнді түрде логикалық сигналдармен анықталатын логикалық құрылғылар.
Цифрлық құрылғылардың тізбектелген функционалдық түйіндер құрамында міндетті жады элементтері болады. Сондықтан бұл құрылғылар жадысы бар автоматтар немесе цифрлық автоматтар (ЦА) деп аталады. Тізбектелген құрылғылардың шығыс сигналдары дәл осы уақыттағы ЦА-ң кірісіндегі сигналдармен ғана емес, сонымен қатар жады элементтерінің күйімен анықталады, ал соңғыларының күйлері алдыңғы келіп түскен кіріс сигналдарының күйіне байланысты. Сонымен, цифрлық автоматтары айнымалылардың (сигналдардың) кіріс жинағының тізбегін шығыс жинағының тізбегіне түрлендіреді. Олардың «тізбектелген құрылғылар немесес схемалар» деп аталуы осыған байланысты
Шифратор (кодер) - кірісіне берілген (кіретін) басқаратын сигналдарды n-разрядты екілік кодқа айналдыруға арналған функциональды түйіншік.
Сонымен қатар, мұндай сигналдар немесе командалар ондық сандар болуы мүмкін, мысалы шифратордың көмегімен екілік кодқа түрленетін командының номері .
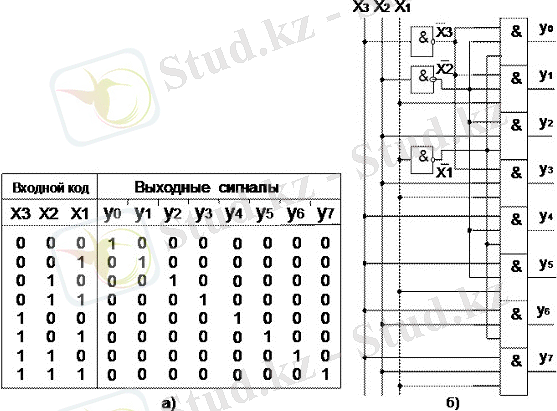
Мысал ретінде 3-разрядты шифратордың сұлбасын жасайық. Алдымен сигналдың коды екілік кодпен берілген, кодтар кестесін (ақиқат кестесін) сызайық. (27, а сурет) . НЕМЕСЕ элементерімен іске асырылған сұлба 27, б суретінде көрсетілген.
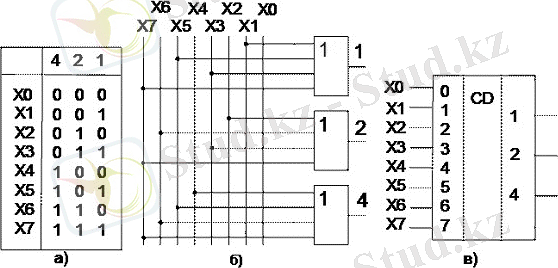
27сурет. 3-разрядты ширатордың кодтар кестесі. а), оның функциональдық сұлбасы б) және ШГБ в) .
Жалпы жағдайда, екілік кодты қолданғанда 2 n кіріс сигналдарын кодтауға болады. Егерде кірісінің біреуіне де жалпы жағдайда кіріс сигналы берілмейтін болса, онда жоғарғыда қаралған сұлбада «000» шығу коды
X 0 кіріске сигнал бергенде баршығыстар болады. X 0 сигналын бірмағаналы идентификация жасау үшін, интегралдық сұлбаларда тағы бір сигнал қалыптасады, ол кіріс сигналдың берілуінің белгісі, бұл басқа мақсаттарда да қолданылады. 28 суретте 3 разрядты басым (приортетті) 8 кірісі бар шифратордың ШГБ(шарты графикалық белгісі) көрсетілген
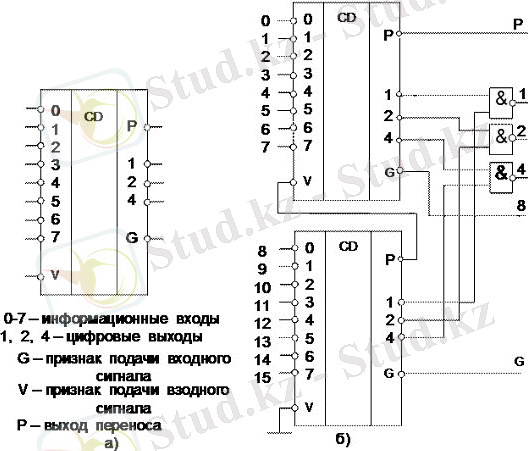
28сурет. 3-разрядты басым (приоритетті) шифратор К555ИВ1 а) және екі МС жалғағаны б)
Кез келген кірісіне сигнал берілгенде, G=1, P=0 болып тағайындаладыда, ал цифрлық шығыстарында-сигнал берілген кірістің номерінің екілік коды
шығады. Егерде сигнал біруақытта екі немесе бірнеше кіріске берілсе, онда шығысында үлкен номері бар кірістің коды тағайындалады. Осыдан шифратордың аты басым (приоритетті) деп аталады.
Егер 0…7 кірістерінің біріне сигнал (лог. «0») берілсе, DD3 шығыстарында тура кодтың кіші разрядтары пайда болады, ал G DD1 шығысында- лог. «0», егерде 8…15 кірістерінің біріне лог. «0» берілсе, онда Р кірісінен берілген лог. «1» DD2 DD1-ің жұмыс істеуіне тиым салады. Бұл жағдайда DD3кіші разрядтары DD2, микросхемамен анықталады, ал 8 крістің шығысында шығыс коды лог. «1» болады. Сонымен 1, 2, 4, 8шығысынан кіріс сигнал берілген кірістің номеріне сәйкес тура код алуға болады
Дешифраторлар (декодерлар)
n кірістің кіреберісіндегі кодқа тәуелді, тек қана өзінің 2 n кірістерінің бірінде «лог. 1» (жоғарғы деңгейдегі дешифратор) немесе «лог. 1» (төменгі деңгейдегі дешифратор) сигналын тудыратын функционалдық түйіншік дешифратор деп аталады.
Дешифратор - функциональный узел, вырабатывающий сигнал «лог. 1» (дешифратор высокого уровня) или сигнал «лог. 0» (дешифратор низкого уровня) только на одном из своих 2 n выходах в зависимости от кода двоичного числа на n входах.
Дешифраторлар басқару құрылғыларында кеңінен қолдынылады. Олар кірісіндегі сигналға сәйкес қандай бірорындаушы құрылғыға әсер ететін
басқаратын сигнал қалыптастырады
Дешифраторлардың интегральды микросхемаларды қосымша кірістерімен жасайды, мысалы рұқсат беретін кіріспен (стробтау) . Стробтау оның жұмысын кірісіндегі цифрлық код өзгергенде өту үрдісі уақыт интервалында жұмысына тиым салып, кірісінде жалған сигналдардың пайда болдырмайды.
ИД3 (30 сурет) микросхемасының 4адресті кірісі бар1, 2, 4, 8 екілік кодының салмақтық коэффициенті бар, стробтайтын S екі инверсті кіріс, ЖӘНЕ мен біріктірген, және 0-15 дейін 16 инверсті кірісі бар.
Егер стробтаудың екі кірісінде «лог. 0», онда номері кіріс кодының ондық эквивалентіне сәйкес шығыста «лог. 0» болады. Егерде S стробтайтын кірістердің бірінде «лог. 1» болса, онда шығысында кірістерінің жағдайына байланысыз «лог. 1». қалыптасады.
Екі стробтау кірісінің барлығы микросхемалардың қолданылуының мұмкіндігін кеңейтеді. Бір инвертормен толықтырылған ИД3 екі микросхемадан 32 кірісі бар дешифратор(31сурет), жинауға болады, ал 17 микросхемадан-256 кірісі бар дешифраторды(32сурет) .
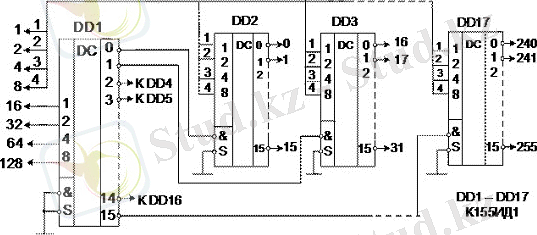
32сурет. 256 шығысы бар дешифратор
2. 3 D-триггерлер
Шығысындағы логикалық мәндері қазіргі уақыт мезетінде, кірісіндегі логикалық сигналдардың жиынтығымен ғана емес, ішкі жады элементерінің оның алдыңғы жұмыс істеу нәтижесінің салдарына байлынысты күйімен анықталатын элктронды цифрлық құрылғыларды тізбекті типті цифрлық құрылғылар немесе жадысы бар цифрлық автоматтар дейді. Алдынғы күйін еске сақтау тригерлердің және жады регистрлердің көмегімен орындалады. Импульстер санауштары және ығысу регистрлері жадысы бар логикалық автоматтардың типтік үлгісі болып саналады.
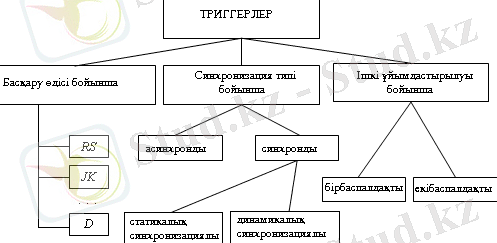
Триггерлер
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz