Кез-келген күштер жүйесі

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Қазақстандық қазіргі заман «Болашақ» академиясының колледжі

КУРСТЫҚ ЖҰМЫС

Пәні: «Техникалық механика негіздері»

Тақырыбы: «Кез-келген күштер жүйесі»

Орындаған: Мылтық Д.

Тобы: ЭРМТ-12

Тексерген: Бектілеуова С. К.

Ақтау - 2014 ж.

МАЗМҰНЫ:

КІРІСПЕ . . . 3

І. ТЕХНОЛОГИЯЛЫҚ БӨЛІМ . . . 4

Күшті берілген центрге келтіру . . . 4
Кез келген күштер жүйесін берілген центірге келтіру . . . 5

1. 3. Кез келген күштер жүйесін қарапайым түрге келтіру . . . 7

1. 4. Кез келген күштер жүйесінің тепе теңдік шарттары . . . 11

ІІ. ЕСЕПТІК БӨЛІМ . . . 12

2. 1. Кеңістікте кез келген бағытта бағытталған күштер жүйесіне арналған есептер . . . 12

ҚОРЫТЫНДЫ . . . 24

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 25

КІРІСПЕ

Теориялық механика пәні материалды денелердің бір-біріне көрсеткен әсерін және механикалық қозғалыстардың жалпы заңдарын зерттейтін пән.
Уақыт өтуімен байланысты кеңістікте материалды денелердің бір-біріне қатысты орын ауыстыруы механикалық қозғалыс деп аталады.
Дененің барлық қаситеттерін есепке алған түрде орын алатын механикалық құбылыстарды теориялық және практикалық тұрғыдан зерттеу өте күрделі. Сондықтан механикада материалды нүкте және абсолют қатты дене ұғымдары енгізіледі.

Механикалық қозғалысты немесе дененің тепе-теңдігін зерттеген кезде өлшемдері және формасының маңызы болмайтын дене, материалды нүкте деп аталады.

Дене қозғалысын қарастырғанда оның кез-келген екі нүктесінің арасындағы қашықтық әрқашан өзгермейтін болса, ол абсолют қатты дене делінеді.

Табиғатта абсолют қатты дене жоқ, кез-келген дене шамалы болса да, деформацияланады. Егер бұл өзгеріс дене өлшемдеріне қатысты өте кіші болса, механикалық қозғалысты зерттеуде бұл өзгеріс назарға алынбайды.
Теориялық механиканың негізгі заңдары бақылау және тәжірибе нәтижелеріне негізделеді.

Біз үйренетін теориялық механика Г. Галилей (1564-1642) және И. Ньютон (1643-1727) тарапынан баяндалған заңдарға негізделген болып, классикалық механика деп аталады. Классикалық механикада уақыт және кеңістік денелердің қозғалысына байланысты емес деп қарастырылады. Сондай-ақ дененің массасы оның жылдамдығына байланысты емес тұрақты шама деп алынады.

І. ТЕХНОЛОГИЯЛЫҚ БӨЛІМ

Күшті берілген центрге келтіру

Әсер сызықтары кеңістікте (жазықтықта) кез-келген түрде орналасқан күштерден құралған жүйе кеңістіктегі (жазықтықтағы) кез-келген күштер жүйесі делінеді. Кез-келген күштер жүйесі әсеріндегі дене жағдайын немесе тепе-теңдігін зерттеу үшін осы күштер қарапайым түрге келтіріледі.

Пуансо леммасы. Күшті бір нүктеден берілген центрге келтіру нәтижесінде келтіру центрінде осы күшке тең болатын күш және оның қосылған жұбы алынады.

Дәлелі. Айталық, дененің А нүктесіне 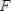күш қойылған болсын (1. 1 сурет) . Бұл күшті кезкелген О нүктеге параллель көшіру үшін 3 аксиомаға сәйкес осы нүктеге 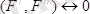күшті қоямыз (1. 1 сурет) .

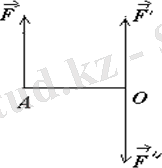
1. 1 сурет

Мұнда

Нәтижеде:

немесе

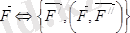
Мұндағы қосылған жұп делінеді. Осы күштің моменті төмендегідей болады:

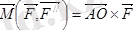
немесе

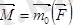Демек:

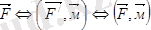Осымен лемма дәлелденеді.

1. 2. Кез келген күштер жүйесін берілген центірге келтіру

Айталық, денеге күштер қойылған болсын. Жоғарыдағы тақырыпқа негізделіп, Пуансо леммасын қолданамыз (1. 2 сурет) .

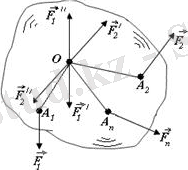
1. 2 сурет 1. 3 сурет

Нәтижеде О нүктеде 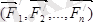күштер және 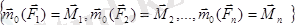қосылған жұптар пайда болады. Егерде күштердің әсер сызықтары кеңістікте болса, жұп моменттерінің векторлары геометриялық; жазықтықта болса, алгебралық қосылады. күштер қиылысатын күштер жүйесі болғандықтан олар геометриялық қосылады.

Нәтижеде:

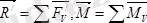(1. 1)

Мұнда 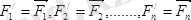болғандықтан (1. 1) -ді төмендегідей жазу мүмкін:

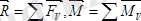(1. 2)

Кезкелген күштер жүйесі жазықтықта орналасқан болса, (1. 2) -ні былай жазамыз:

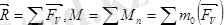(1. 3)

(1. 2) және (1. 3) өрнектердегі 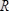күштер жүйесінің бас векторы, ал 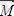бас моменті делінеді.

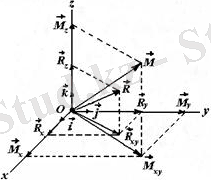
Демек, кезкелген күштерді берілген центрге келтіру нәтижесінде бір бас вектор және бір бас момент алынады (1. 3 сурет) .

Бас вектор және бас моментті аналитикалық тәсілде төмендегідей есептеу мүмкін.

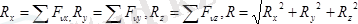(1. 4)

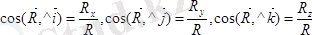(1. 5)

Бас вектор мен бас момент арасындағы бұрышты анықтау үшін бұл векторларды скаляр көбейтеміз:

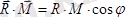немесе

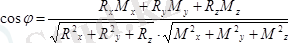(1. 6)

келіп шығады.

1. 3. Кез келген күштер жүйесін қарапайым түрге келтіру

Кезкелген күштерді қарапайым түрге келтіру үшін төмендегі жағдайларды қарастырамыз:

1. Бас вектор 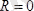, бас момент 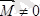болса, кезкелген күштер жүйесі бір бас моментке келтіріледі.

2. Егер бас момент 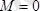, бас вектор 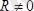болса, күштер жүйесі бас векторға келтіріледі.

3. Бас вектор 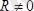және бас момент 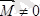болып, олар өзара 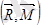перпендикуляр болғанда, кезкелген күштер жүйесі бір бас векторға 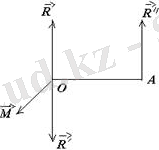келтіріледі. Шынында да, бұл жағдайдың дұрыстығын көрсету үшін бас момент құраушыларын сондай өзгертеміз, нәтижеде 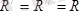болып, ал 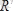бас вектор 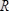бағытталған сызық бойымен қарама-қарсы

бағытталсын (1. 4 сурет) .

1. 4 сурет

Бұл жағдайда 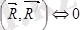болып, О нүктеде АО=М/R қашықтықта 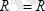орналасады. Демек, А нүктедебір бас вектор алынады.

1. Бас вектормен бас момент , бұл жағдай динамо (динамикалық винт) делінеді.

Бас вектор және бас момент нөлге тең болмаса және олар бір-біріне перпендикуляр болмаса, онда мұндай күштер жүйесі динамоға келтіріледі.

Бұның дұрыстығын көрсету үшін бас моментті құраушыларға жіктейміз. Бұл құраушылардын бірі бас вектор бойымен, екіншісі бас векторға перпендикуляр болсын (1. 5 сурет) .

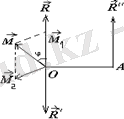
1. 5 сурет 1. 6 сурет

Енді мен 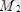- ге 3 жағдайды қолдансақ, О нүктеден 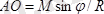қашықтықта бас вектор 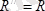алынады. Сонымен, кезкелген күштер жүйесі О нүктедегі моменті 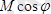болатын 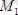жұп моменті векторына және А нүктедегі бас векторға келтіреді. Жұп моментінің векторы еркін болғаны үшін 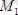-ді А нүктеге көшіру мүмкін. Демек, күштер жүйесі динамоға келтірілді (1. 6 сурет) .

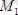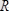және векторлар бағытталған ось центрлік винт өсі делінеді.

Бас вектор және бас момент нөлге тең болса, кезкелген күштер жүйесі тепе-теңдікте болады.

Есеп 1. 1

Қырының ұзындығы а= 10 см кубке, 1. 6 суретте көрсетілгендей, шамалары F= 10 н . бірнеше күш қойылған. Осы күштер жүйесі қарапайым түрге келтірілсін.

Шешуі. Координата басы ретінде А нүктесін қабылдап, Ax, Ay, Az өстерін өткізейік.

Күштердің денеге қойылған нүктелерінің координаталарын анықтайық, яғни

; ; ;

; ; .

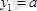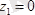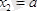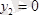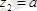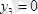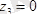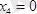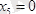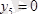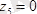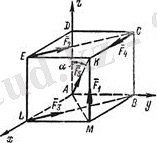
1. 7 сурет

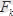күштерінің координат өстеріне болған проекцияларынтабайық

; ; ;

; ; .

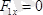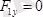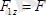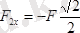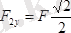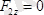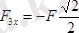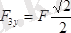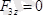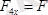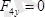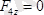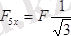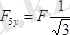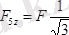күшінің өстерге болған проекцияларын анықтау үшін оны алдын-ала AD және АМ бағыттарына жіктеп алдық. Егер

; .

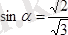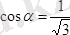екендігін еске алсақ, онда бас вектордың координат өстеріне болған проекциялары болады.

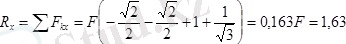
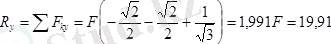
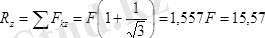
Денеге әсер ететін күштер жүйесінің бас моментінің өстерге болған проекциялары тең.

;

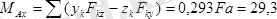
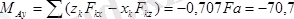
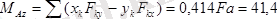
Демек денеге қойылған күштер жүйесінің бас векторы мен оның бас моменті нөлге тең емес. Олай болса бас вектор мен бас моменттің (екінші инвариант) скаляр көбейтіндісі

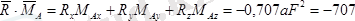
болады.

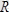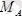Бұдан және векторларыбірбіріне перпендикуляр еместігікөрінеді. Бұл жағдайда күштер

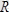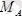Бұдан және векторлары бір-біріне перпендикуляр еместігі көрінеді. Бұл жағдайда күштер жүйесі динамикалық винтке келтіріледі. Динамикалық винт өсінің теңдеуі төмендегідей көрініске ие

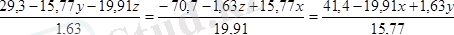Динаманың параметрі

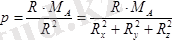формуламен анықталады.

Мұның сан мәні

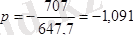см.

болады.

1. 4. Кез келген күштер жүйесінің тепе теңдік шарттары

Кеңістікте орналасқан кез келген күштер жүйесі әсеріндегі дене тепе-теңдікте болуы үшін күштердің бас векторы және бас моменті нөлге тең болуы қажетті және жеткілікті:

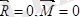(1. 7)

(1. 7) ні декарт координат өстеріне проекциялаймыз:

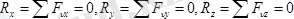(1. 8)

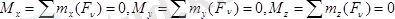
Кез келген күштер жазықтықта орналасқан болса, олардың тепе-теңдік шарты төмендегідей болады:

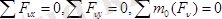(1. 9)

Егерде күштер жүйесі кеңістікте (жазықтықта) қиылысатын күштерден құралған болса, олардың тепе-теңдік шарттары сәйкес түрде былай жазылады:

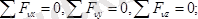(1. 10)

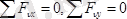(1. 11)

Кез келген күштер жүйесі Oz өсіне параллель болса, (1. 10) -ның алғашқы екеуі және соңғысы тікелей нөлге тең болады. Нәтижеде кеңістіктегі параллель тепе-теңдігінің шарты төмендегідей болады:

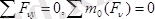(1. 12)

Мұндағы күштер Оу осіне параллель.

ІІ. ЕСЕПТІК БӨЛІМ

2. 1. Кеңістікте кез келген бағытта бағытталған күштер жүйесіне арналған есептер

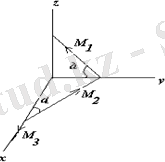
Есеп 2. 1

2. 1 суретте көрсетілген жұп моменттерінің тең әсерлі моментінің модулі табылсын. М ₁ =М ₂ =1Нм, М ₃ =0, 707Нм, =45 ⁰ .

Шешуі. 2. 1 суретте көрсетілген жұп моменттері кеңістікте орналасқан. Кеңістіктегі жұп моменттерінің геометриялық қосындысы олардың бас моментінен тұратыны бізге белгілі.

Жұп моменттерін Ох, Оу, Оz өстеріне проекциялаймыз:

2. 1сурет

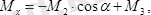
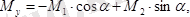
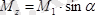
Сан мәндерін қойсақ :

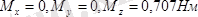
Нәтижеде

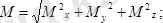M = 0, 707Нм

келіп шығады.

Есеп 2. 2

Салмағы G =1, 6 кН болатын барабан өсіне шынжыр оралған, оның керілуі Т =20 см барабан S шестерняға қойылған күш әсерінде тепе-теңдікте тұрады. және Оу осіне параллель , r ₂ =40 см .

Шестерня центрі А подпятниктен AS =10 см қашықтықта орналасқан. АВ =120 см , SD =40 см . А подпятник, В подшипник реакциялары және 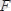күш мөлшері табылсын.

Шешуі . (2. 2сурет, а) дегі барабан тепе-теңдігін тексереміз. А подпятник, В подшипник әсерлесін сәйкес түрде 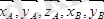реакция күштері мен ауыстырамыз. Онда барабан 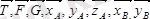күштер әсерінде тепе-теңдікте болады. Бұл күштер кеңістіктегі кез келген күштер жүйесінен тұрады.

Демек, тепе-теңдік теңдеулері төмендегідей болады:

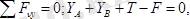
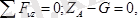
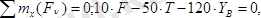
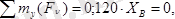
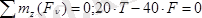
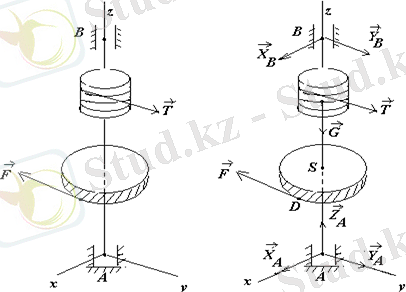
а ә

2. 2 сурет

Сан мәндерін қойсақ:

х _А =0, , у _А =-2, 5кН, z _A =1, 6кН, х _В =0, у _В =-7, 5кН, F=10кН.

Мұндағы (-) таңба у _А , у _В -лардың ақиқат бағыты (2. 2 сурет, ә) -дағыға кері болады.

Есеп 2. 3

Салмағы Р болған тікбұрышты ABCD плита А топсасы, CN , CK стержендер және BS тросы (2. 3 сурет, а ) арқылы горизонталь бекітілген. Стержендердің салмағы есепке алынбаған кездегі, барлық байланыстар топсадан тұрады деп және В нүктесіне салмағы Q болған М жүгі ілінген болса А нүктесіндегі реакция күші, стержендердегі және тростағы белгісіз ішкі күштер анықталсын. A, B, C, D, L, E, F, K нүктелер параллелепипед тікбұрыштарының ұштарына орналасқан. Олардың қабырғалары CD =3 а ; CB =4 а ; CE =5 а тең. Тростың бекітілген S нүктесі FD сызығының жалғасында жатыр және SBD =45 ⁰ .

Шешуі. Плитаның тепе-теңдігін қарастырайық. Оған белгілі 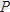және күштері әсер етеді. А нүктесі, CN , CK стержендер және BS тросы плитаға, қойылған байланыстар. Бұл байланыстардан ойша босанайық. А топсадағы реакция күшінің әсер ететін бағыты белгісіз. Сол себебтен реакция күшін координата өстерінің бағыттары бойынша үш 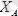, , 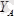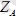күштеріне жіктейміз(2. 3 сурет, б ) . Стержендердің салмақтары есепке алынбағаны үшін және оларды байланыстратын нүктелер топса-салар болғандықтан стержендердегі белгісіз ішкі күштер олардың бойымен бағытталады, яғни стержендер сығылған немесе созылған күйде болуы мүмкін.

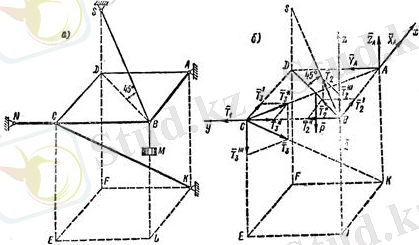
Описание: 20

2. 3 сурет

Оларды созылатын стержендер деп қабылдайық. Мұндай жағдайда ішкі күштерді 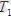және 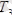деп белгілеп, тасталатын стержендерге қарай бағыттайық. Трос реакциясын 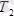деп белгілейік,

Сонымен плита кеңістіктегі 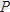, , 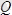, , 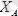, , 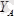, 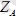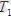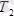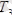күштер жүйесінің әсерінде. Бұл күштер жүйесі өзінің тепе-теңдігін сақтағаны үшін оған орынды болған алты теңдеу түзіледі. Есепте белгісіздер саны алтау, яғни 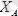, , 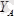, , 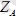, 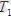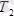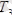. Демек бұл есеп статикалық анықталатын есептер құрамына жатады.

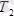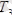Белгісіз ішкі және күштерін алдын-ала таңдап алынған координат өстері бойынша жайғанымыз орынды, яғни

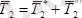Сонымен қатар BD бойымен бағытталған 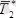күші төмендегі көріністе жайылады

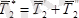Онда

, , ,

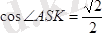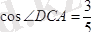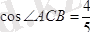еске ала отырып

; ;

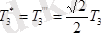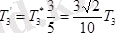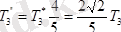
табамыз.

Плитаның тепе-теңдігін анықтайтын теңдеулер былай жазылады

;

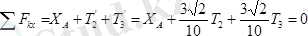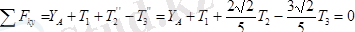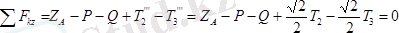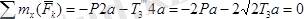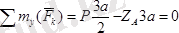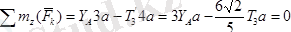Бұл теңдеулерді шешіп

; ; ;

; ;

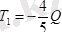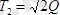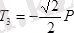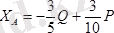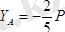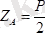
анықтаймыз.

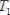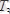Табылған және күштердегі «минус» таңбалары, олардың сығылатынын көрсетеді. Егер сатының салмағы 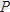болып, ол оның ортасына қойылған болса, онда

; ; ; ;

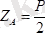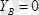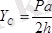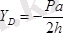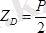
Есеп 2. 4 Тісті редуктордың I білігіне (2. 4 сурет, а) оны айналдыратын моменті 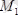-ге тең күш қойылған. Бұл редуктор өзінің тепе-теңдігін сақтау үшін IV білікке моменті 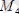- ке тең болған қандай күш қойылуы қажет? Подшипниктердегі үйкеліс күші есепке алынбасын. Барлық керек өлшемдер суретте көрсетілген.

Шешуі . Берілген механизм үш денеден құралған - дөңгелегі 1 болған I біліктен, дөңгелекетері 2 және 3 болған II біліктен және дөңгелегі 4 болған IV біліктен. Әрбір дененің жеке-жеке тепе-теңдігін қарастырайық.

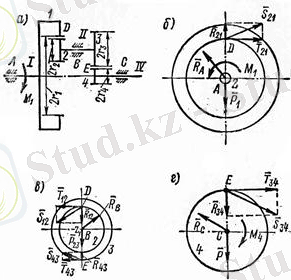
Описание: 23

2. 4 сурет

Дөңгелегі 1 болған I - білік үшін (2. 4 сурет, б ) . Бұл білікке 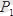, моменті 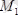болған жұп күш, подшипник реакциясы 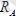және 2 дөңгелектің реакция күші 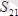әсер етеді. Дөңгелектің реакция күші- 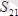I білікке перпендикуляр болған жазықтықтың бетінде жатады. Бұл күшті екі күшке жіктейміз. Оның бірі 1 ( 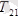) - дөңгелекке жанама бойлап бағытталса, екіншісі ( 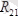) дөңгелектің радиусы бойлап бағытталады, яғни

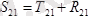Аталған күштер 1 дөңгелектің D нүктесіне қойылған. Есепте подшипник реакциясын табудың қажеттілігі жоқтығынан, ол енбейтін тепе - теңдік теңдеуін түземіз. Мұндай теңдеу I (ось z ) біліктің өсіне қатысты алынған моменттер теңдеуі болып есептелінеді, яғни

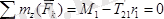Бұл өрнектен

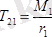
келіп шығады.

Дөңгелектері 2 және 3 болған II (2. 4сурет, в ) - ось үшін. D нүктесінде 1 дөңгелектің 2 дөңгелекке көрсететін ықпалы

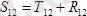Сонымен қатар

; ; .

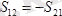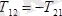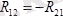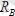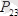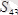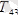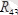Подшипниктің реакция күшін деп белгілейік. Дөңгелектің салмағы- , 4 - дөңгелектің 3 - кекөрсеткен әсері- . Бұл реакция күшін және күштеріне жіктейік. Күш Е нүктесіне қойылған. II (ось z ₁ ) -білік өсіне қатысты моменттер теңдеуін түзейік. Онда

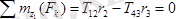
Бұл өрнектен

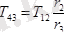
Егер

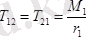
екенін еске алсақ, онда

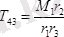
Дөңгелегі 4 (2. 4сурет, г ) болған IV білік үшін. 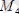- анықталатын момент болсын.

Онда жоғарыда көрсетілген әдіс бойынша,

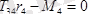
болады. Демек

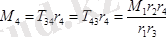Есеп 2. 5

Салмағы Р және Q болған АВ мен ВС біртекті екі стержень А және С нүктелеріне топса арқылы, ал стержендерді қосушы В топсада олар жылтыр вертикаль қабырғада еркін жатыр (2. 5 сурет, а ) . Егер АВС үшбұрышы горизонтпен 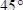бұрыш құрап және болған кездегі А және С топсаларындағы реакция күштері мен N- ге тең болған қабырғаның реакция күші анықталсын.

Шешуі. Егер барлық жүйені тұтас дене деп қарастырсақ, онда статикалық анықталмайтын есепке тірелеміз. Себебі жеті белгісізді анықтауымыз керек, яғни олар А және С топсалардағы реакция күштері мен қабырғаның реакция күші болып есептелінеді. Сондықтан да берілген жүйенің тепе-теңдігін АВ және ВС стержендердің жеке-жеке тепе-теңдіктері деп қарастырамыз.

Алдымен АВ стерженнің (2. 5 сурет, б) тепе-теңдігін зерттейік. Бұл стерженге D нүктесіне қойылған оның салмағы 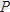әсер етеді. А және В нүктелеріндегі сфералық топсалар байланыстар қызметін атқарады. Байланыс реакция күштері 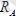және 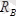-лардың кеңістікте алатын бағыттары белгісіз. Сондықтан оларды координата өсьтері бойынша 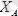, , 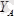, , 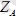, 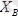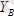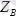құраушыларға жаямыз.

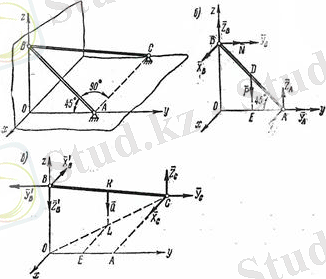
Описание: 25

2. 5 сурет

Қабырғаның реакция күші 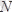тек АВ стержень бойлап әсер етеді. Онда АВ стерженнің тепе-теңдік теңдеулері төмендегідей жазылады

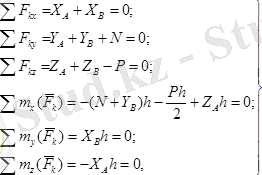
Бұл жердегі

BO=AO=h.

Енді ВС стержені (2. 5 сурет, в ) үшін тепе-теңдік шарттарын анықтайық. Оған ауырлық күші 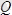, С және В топсаларының реакция күштері 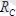, 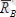әсер етеді және 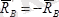, яғни 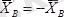, т. т. Онда ВС стерженінің тепе-теңдік теңдеулері.

Бұл жерде

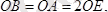
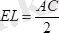Түзілген теңдеулерді шеше отырып

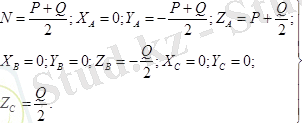
табамыз.

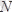күші ВС стержень бойлап бағытталған болса, онда жоғарыдағы теңдеулер былай жазылады

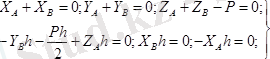
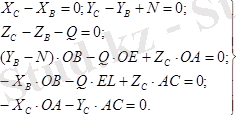
Бұл теңдеулерді шеше отырып

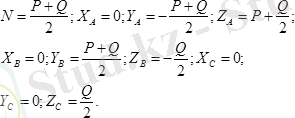
анықтаймыз.

Сонымен

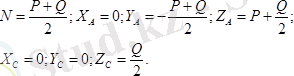
Есеп 2. 6

плитасына 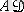қабырғасымен бағытталған 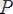күшi нүктесiнен түсiп тұр (2. 6 сурет, а) . Плитаны тепе-теңдiкте ұстап тұрған алты салмақсыз стерженьдердiң реакцияларын анықтаңыздар.